Phần sau đây mô tả ngữ nghĩa của các thao tác được xác định trong giao diện XlaBuilder. Thông thường, các thao tác này liên kết 1 với một với các thao tác được xác định trong giao diện RPC trong xla_data.proto.
Lưu ý về cách đặt tên: kiểu dữ liệu tổng quát mà XLA xử lý là một mảng N chiều chứa các phần tử thuộc một số loại đồng nhất (chẳng hạn như số thực 32 bit). Xuyên suốt tài liệu, mảng được dùng để biểu thị một mảng có kích thước tuỳ ý. Để thuận tiện, các trường hợp đặc biệt sẽ có tên cụ thể và quen thuộc hơn; ví dụ: vectơ là mảng 1 chiều và ma trận là mảng 2 chiều.
AfterAll
Xem thêm XlaBuilder::AfterAll.
AfterAll lấy một số lượng lớn mã thông báo và tạo ra một mã thông báo duy nhất. Mã thông báo là các loại gốc có thể được tạo luồng giữa các thao tác có hiệu ứng phụ để thực thi thứ tự. Bạn có thể dùng AfterAll làm một chuỗi mã thông báo để sắp xếp một thao tác sau một thao tác đặt.
AfterAll(operands)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operands |
XlaOp |
số lượng mã thông báo đa dạng |
AllGather
Xem thêm XlaBuilder::AllGather.
Thực hiện nối trên các bản sao.
AllGather(operand, all_gather_dim, shard_count, replica_group_ids,
channel_id)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand
|
XlaOp
|
Mảng để nối các bản sao |
all_gather_dim |
int64 |
Phương diện nối |
replica_groups
|
vectơ của các vectơ của int64 |
Các nhóm thực hiện nối |
channel_id
|
không bắt buộc int64
|
Mã nhận dạng kênh không bắt buộc để giao tiếp giữa các mô-đun |
replica_groupslà danh sách các nhóm bản sao mà quá trình nối được thực hiện (mã nhận dạng bản sao cho bản sao hiện tại có thể được truy xuất bằng cách sử dụngReplicaId). Thứ tự của các bản sao trong mỗi nhóm sẽ xác định thứ tự đặt dữ liệu đầu vào của các bản sao đó trong kết quả.replica_groupsphải trống (trong trường hợp này, tất cả bản sao thuộc về một nhóm duy nhất, được sắp xếp từ0đếnN - 1) hoặc chứa cùng số phần tử với số lượng bản sao. Ví dụ:replica_groups = {0, 2}, {1, 3}thực hiện việc nối giữa các bản sao0và2, cũng như1và3.shard_countlà kích thước của từng nhóm bản sao. Chúng ta cần điều này trong trường hợpreplica_groupstrống.channel_idđược dùng để giao tiếp giữa các mô-đun: chỉ các thao tácall-gathercó cùngchannel_idmới có thể giao tiếp với nhau.
Hình dạng đầu ra là hình dạng đầu vào với all_gather_dim lớn hơn shard_count lần. Ví dụ: nếu có hai bản sao và toán hạng có giá trị [1.0, 2.5] và [3.0, 5.25] tương ứng trên hai bản sao, thì giá trị đầu ra từ toán tử này (trong đó all_gather_dim là 0) sẽ là [1.0, 2.5, 3.0,
5.25] trên cả hai bản sao.
AllReduce
Xem thêm XlaBuilder::AllReduce.
Thực hiện một phép tính tuỳ chỉnh trên các bản sao.
AllReduce(operand, computation, replica_group_ids, channel_id)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand
|
XlaOp
|
Mảng hoặc một bộ dữ liệu không trống của mảng để giảm bớt các bản sao |
computation |
XlaComputation |
Tính toán rút gọn |
replica_groups
|
các vectơ của int64 |
Các nhóm thực hiện việc rút gọn |
channel_id
|
int64 không bắt buộc
|
Mã nhận dạng kênh không bắt buộc để giao tiếp giữa các mô-đun |
- Khi
operandlà một bộ dữ liệu mảng, quá trình cắt giảm sẽ được thực hiện trên từng phần tử của bộ dữ liệu đó. replica_groupslà danh sách các nhóm bản sao mà trong đó quá trình rút gọn được thực hiện (có thể truy xuất mã bản sao cho bản sao hiện tại bằng cách sử dụngReplicaId).replica_groupsphải trống (trong trường hợp này, tất cả bản sao thuộc về một nhóm duy nhất) hoặc chứa cùng số lượng phần tử với số lượng bản sao. Ví dụ:replica_groups = {0, 2}, {1, 3}thực hiện việc giảm thiểu các bản sao0và2, cũng như1và3.channel_idđược dùng để giao tiếp giữa các mô-đun: chỉ các thao tácall-reducecó cùngchannel_idmới có thể giao tiếp với nhau.
Hình dạng đầu ra giống với hình dạng đầu vào. Ví dụ: nếu có hai bản sao và toán hạng có giá trị [1.0, 2.5] và [3.0, 5.25] tương ứng trên hai bản sao, thì giá trị đầu ra từ toán tử này và phép tính tổng sẽ là [4.0, 7.75] trên cả hai bản sao. Nếu dữ liệu đầu vào là một bộ dữ liệu, thì dữ liệu đầu ra cũng là một bộ dữ liệu.
Quá trình tính toán kết quả của AllReduce yêu cầu phải có một dữ liệu đầu vào từ mỗi bản sao, vì vậy, nếu một bản sao thực thi một nút AllReduce nhiều lần hơn một bản sao khác, thì bản sao cũ sẽ đợi vĩnh viễn. Vì tất cả các bản sao đều đang chạy cùng một chương trình, nên không có nhiều cách để điều đó xảy ra, nhưng có thể xảy ra khi điều kiện của vòng lặp while phụ thuộc vào dữ liệu từ nguồn cấp dữ liệu và dữ liệu được đưa vào khiến vòng lặp while lặp lại nhiều lần hơn trên một bản sao khác.
AllToAll
Xem thêm XlaBuilder::AllToAll.
AllToAll là một thao tác tập thể gửi dữ liệu từ tất cả lõi đến tất cả lõi. Quá trình này gồm hai giai đoạn:
- Giai đoạn tán xạ. Trên mỗi lõi, toán hạng được chia thành số
split_countkhối dọc theosplit_dimensionsvà các khối này được phân tán đến tất cả lõi, ví dụ: khối thứ i được gửi đến lõi thứ i. - Giai đoạn thu thập. Mỗi lõi nối các khối đã nhận dọc theo
concat_dimension.
Các lõi tham gia có thể được định cấu hình bằng cách:
replica_groups: mỗi ReplicaGroup chứa một danh sách mã nhận dạng bản sao tham gia vào quá trình tính toán (có thể truy xuất mã nhận dạng bản sao hiện tại bằngReplicaId). AllToAll sẽ được áp dụng trong các nhóm con theo thứ tự được chỉ định. Ví dụ:replica_groups = { {1,2,3}, {4,5,0} }có nghĩa là AllToAll sẽ được áp dụng trong các bản sao{1, 2, 3}và trong giai đoạn thu thập, đồng thời các khối đã nhận sẽ được nối theo cùng một thứ tự là 1, 2, 3. Sau đó, một AllToAll khác sẽ được áp dụng trong bản sao 4, 5, 0 và thứ tự nối cũng là 4, 5, 0. Nếureplica_groupstrống, tất cả bản sao sẽ thuộc một nhóm, theo thứ tự nối của các bản sao đó.
Điều kiện tiên quyết:
- Kích thước chiều của toán hạng trên
split_dimensioncó thể chia hết chosplit_count. - Hình dạng của toán hạng không phải là bộ dữ liệu.
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng đầu vào n chiều |
split_dimension
|
int64
|
Một giá trị trong khoảng [0,
n) đặt tên cho phương diện mà theo đó toán hạng được phân tách |
concat_dimension
|
int64
|
Một giá trị trong khoảng [0,
n) đặt tên cho phương diện mà theo đó các khối phân tách được nối |
split_count
|
int64
|
Số lượng lõi tham gia hoạt động này. Nếu replica_groups trống, thì đây phải là số lượng bản sao; nếu không, số lượng này phải bằng số lượng bản sao trong mỗi nhóm. |
replica_groups
|
Vectơ ReplicaGroup
|
Mỗi nhóm chứa một danh sách mã bản sao. |
Dưới đây là ví dụ về Alltoall.
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(x, /*split_dimension=*/1, /*concat_dimension=*/0, /*split_count=*/4);
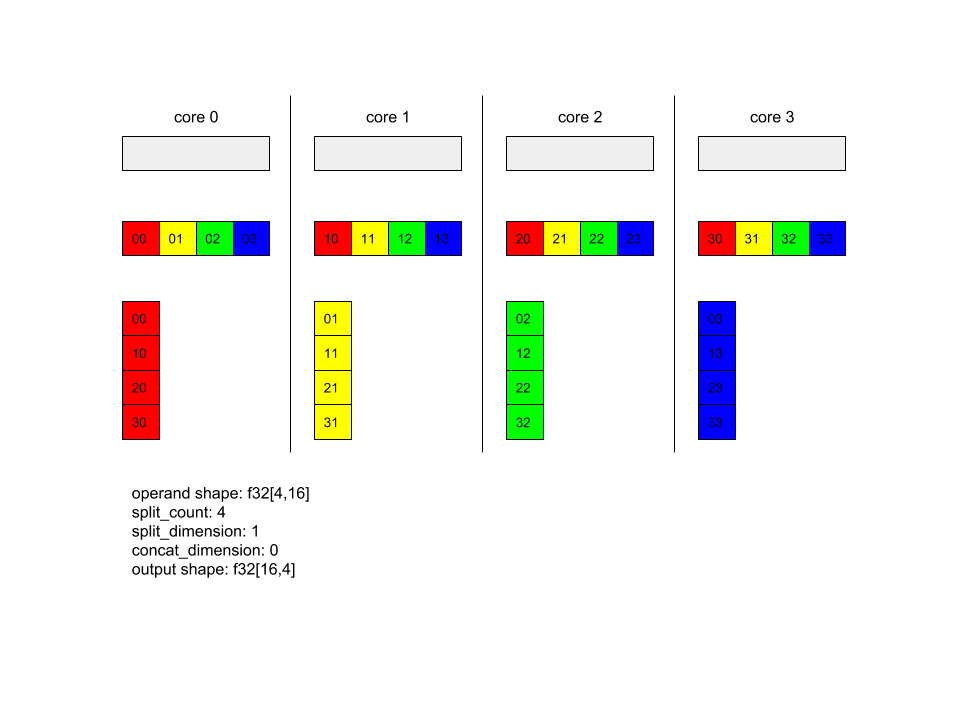
Trong ví dụ này, có 4 lõi tham gia vào Alltoall. Trên mỗi lõi, toán hạng được chia thành 4 phần dọc theo phương diện 0, vì vậy, mỗi phần có hình dạng f32[4,4]. 4 phần này được phân tán cho tất cả các lõi. Sau đó, mỗi lõi nối các phần đã nhận theo chiều 1 theo thứ tự lõi 0-4. Do đó, đầu ra trên mỗi lõi có hình dạng f32[16,4].
BatchNormGrad
Xem thêm XlaBuilder::BatchNormGrad và bài báo ban đầu về chuẩn hoá theo lô để biết thông tin mô tả chi tiết về thuật toán này.
Tính toán độ dốc của chuẩn lô.
BatchNormGrad(operand, scale, mean, variance, grad_output, epsilon, feature_index)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng n chiều cần được chuẩn hoá (x) |
scale |
XlaOp |
Mảng 1 chiều () |
mean |
XlaOp |
Mảng 1 chiều () |
variance |
XlaOp |
Mảng 1 chiều () |
grad_output |
XlaOp |
Độ dốc được truyền đến BatchNormTraining () |
epsilon |
float |
Giá trị Epsilon () |
feature_index |
int64 |
Chỉ mục đến phương diện tính năng trong operand |
Đối với mỗi đặc điểm trong phương diện đặc điểm (feature_index là chỉ mục cho phương diện đặc điểm trong operand), toán tử này sẽ tính toán độ dốc tương ứng với operand, offset và scale trên tất cả các phương diện khác. feature_index phải là một chỉ mục hợp lệ cho phương diện tính năng trong operand.
Ba độ dốc này được xác định bằng các công thức sau (giả sử một mảng 4 chiều là operand và với chỉ mục kích thước của tính năng là l, kích thước lô m và kích thước không gian là w và h):
Các đầu vào mean và variance đại diện cho các giá trị thời điểm trên phương diện lô và không gian.
Loại đầu ra là một bộ dữ liệu gồm 3 tay điều khiển:
| Kết quả đầu ra | Loại | Ngữ nghĩa |
|---|---|---|
grad_operand
|
XlaOp
|
độ dốc theo dữ liệu đầu vào operand () |
grad_scale
|
XlaOp
|
chuyển màu đối với đầu vào scale () |
grad_offset
|
XlaOp
|
chuyển màu đối với đầu vào offset() |
BatchNormInference
Xem thêm XlaBuilder::BatchNormInference và bài báo gốc về chuẩn hoá theo lô để biết nội dung mô tả chi tiết về thuật toán này.
Chuẩn hoá một mảng trên các phương diện theo lô và không gian.
BatchNormInference(operand, scale, offset, mean, variance, epsilon, feature_index)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
mảng n chiều cần được chuẩn hoá |
scale |
XlaOp |
Mảng 1 chiều |
offset |
XlaOp |
Mảng 1 chiều |
mean |
XlaOp |
Mảng 1 chiều |
variance |
XlaOp |
Mảng 1 chiều |
epsilon |
float |
Giá trị epsilon |
feature_index |
int64 |
Chỉ mục cho phương diện nổi bật trong operand |
Đối với mỗi đặc điểm trong phương diện đặc điểm (feature_index là chỉ mục cho phương diện đặc điểm trong operand), toán tử này sẽ tính toán giá trị trung bình và phương sai trên tất cả các phương diện khác, đồng thời sử dụng giá trị trung bình và phương sai để chuẩn hoá từng phần tử trong operand. feature_index phải là một chỉ mục hợp lệ cho nhóm tính năng trong operand.
BatchNormInference tương đương với việc gọi BatchNormTraining mà không cần tính mean và variance cho mỗi lô. Thay vào đó, hàm này sử dụng mean và variance đầu vào làm giá trị ước tính. Mục đích của toán tử này là giảm độ trễ trong quá trình suy luận, do đó có tên là BatchNormInference.
Kết quả là một mảng n chiều, được chuẩn hoá có cùng hình dạng với operand đầu vào.
BatchNormTraining
Xem thêm XlaBuilder::BatchNormTraining và the original batch normalization paper để biết nội dung mô tả chi tiết về thuật toán.
Chuẩn hoá một mảng theo kích thước lô và không gian.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng n chiều cần được chuẩn hoá (x) |
scale |
XlaOp |
Mảng 1 chiều () |
offset |
XlaOp |
Mảng 1 chiều () |
epsilon |
float |
Giá trị epsilon () |
feature_index |
int64 |
Chỉ mục đến phương diện tính năng trong operand |
Đối với mỗi đặc điểm trong phương diện đặc điểm (feature_index là chỉ mục cho phương diện đặc điểm trong operand), toán tử này sẽ tính giá trị trung bình và phương sai trên tất cả các phương diện khác, đồng thời sử dụng giá trị trung bình và phương sai để chuẩn hoá từng phần tử trong operand. feature_index phải là chỉ mục hợp lệ cho phương diện tính năng trong operand.
Thuật toán diễn ra như sau cho mỗi lô trong operand chứa các phần tử m với w và h là kích thước của kích thước không gian (giả sử operand là một mảng 4 chiều):
Tính toán giá trị trung bình của lô cho mỗi đặc điểm
ltrong phương diện đặc điểm:Tính toán độ lệch chuẩn của lô : $\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
Chuẩn hoá, điều chỉnh theo tỷ lệ và dịch chuyển:
Giá trị epsilon, thường là một số nhỏ, được thêm vào để tránh lỗi chia cho 0.
Loại dữ liệu đầu ra là một bộ dữ liệu gồm 3 XlaOp:
| Kết quả đầu ra | Loại | Ngữ nghĩa |
|---|---|---|
output
|
XlaOp
|
mảng n chiều có cùng hình dạng với dữ liệu đầu vào operand (y) |
batch_mean |
XlaOp |
Mảng 1 chiều () |
batch_var |
XlaOp |
Mảng 1 chiều () |
batch_mean và batch_var là các khoảnh khắc được tính toán trên phương diện không gian và lô bằng các công thức ở trên.
BitcastConvertType
Xem thêm XlaBuilder::BitcastConvertType.
Tương tự như tf.bitcast trong TensorFlow, thực hiện phép toán bitcast thông minh từ hình dạng dữ liệu đến hình dạng mục tiêu. Kích thước đầu vào và đầu ra phải khớp nhau: ví dụ: các phần tử s32 trở thành phần tử f32 thông qua quy trình bitcast và một phần tử s32 sẽ trở thành bốn phần tử s8. Bitcast được triển khai dưới dạng một phép truyền cấp thấp, vì vậy, các máy có cách biểu diễn dấu phẩy động khác nhau sẽ cho ra kết quả khác nhau.
BitcastConvertType(operand, new_element_type)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
mảng thuộc loại T với kích thước D |
new_element_type |
PrimitiveType |
loại U |
Kích thước của toán hạng và hình dạng mục tiêu phải khớp nhau, ngoại trừ chiều cuối cùng sẽ thay đổi theo tỷ lệ kích thước gốc trước và sau khi chuyển đổi.
Loại phần tử nguồn và đích không được là bộ dữ liệu.
Chuyển đổi bitcast sang loại nguyên gốc có chiều rộng khác nhau
Lệnh HLO BitcastConvert hỗ trợ trường hợp kích thước của loại phần tử đầu ra T' không bằng kích thước của phần tử đầu vào T. Vì toàn bộ thao tác về mặt khái niệm là một bitcast và không thay đổi các byte cơ bản, nên hình dạng của phần tử đầu ra phải thay đổi. Đối với B = sizeof(T), B' =
sizeof(T'), có hai trường hợp có thể xảy ra.
Trước tiên, khi B > B', hình dạng đầu ra sẽ nhận được kích thước nhỏ nhất mới có kích thước B/B'. Ví dụ:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
Quy tắc này vẫn giữ nguyên đối với các đại lượng vô hướng hiệu quả:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
Ngoài ra, đối với B' > B, hướng dẫn này yêu cầu kích thước logic cuối cùng của hình dạng đầu vào phải bằng B'/B và kích thước này sẽ bị loại bỏ trong quá trình chuyển đổi:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
Xin lưu ý rằng các lượt chuyển đổi giữa các chiều rộng bit khác nhau không phải theo phần tử.
Truyền
Xem thêm XlaBuilder::Broadcast.
Thêm phương diện vào một mảng bằng cách sao chép dữ liệu trong mảng đó.
Broadcast(operand, broadcast_sizes)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng cần sao chép |
broadcast_sizes |
ArraySlice<int64> |
Kích thước của phương diện mới |
Các phương diện mới được chèn ở bên trái, tức là nếu broadcast_sizes có giá trị {a0, ..., aN} và hình dạng toán hạng có phương diện {b0, ..., bM} thì hình dạng của kết quả sẽ có phương diện {a0, ..., aN, b0, ..., bM}.
Phương diện mới chỉ mục vào các bản sao của toán hạng, tức là
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
Ví dụ: nếu operand là f32 vô hướng có giá trị 2.0f và broadcast_sizes là {2, 3}, thì kết quả sẽ là một mảng có hình dạng f32[2, 3] và tất cả giá trị trong kết quả sẽ là 2.0f.
BroadcastInDim
Xem thêm XlaBuilder::BroadcastInDim.
Mở rộng kích thước và thứ hạng của một mảng bằng cách sao chép dữ liệu trong mảng.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng cần sao chép |
out_dim_size |
ArraySlice<int64> |
Kích thước của các kích thước của hình dạng mục tiêu |
broadcast_dimensions |
ArraySlice<int64> |
Phương diện nào trong hình dạng mục tiêu tương ứng với mỗi phương diện của hình dạng toán hạng |
Tương tự như Thông báo truyền tin, nhưng cho phép thêm các phương diện ở mọi nơi và mở rộng các phương diện hiện có với kích thước bằng 1.
operand được truyền đến hình dạng do out_dim_size mô tả.
broadcast_dimensions liên kết các kích thước của operand với các kích thước của hình dạng mục tiêu, tức là kích thước thứ i của toán hạng được liên kết với kích thước thứ broadcast_dimension[i] của hình dạng đầu ra. Kích thước của operand phải có kích thước 1 hoặc có cùng kích thước với kích thước trong hình dạng đầu ra mà chúng được ánh xạ đến. Các phương diện còn lại được điền bằng các phương diện có kích thước 1. Sau đó, tính năng truyền phát kích thước thoái hoá sẽ truyền phát dọc theo các kích thước thoái hoá này để đạt được hình dạng đầu ra. Ngữ nghĩa được mô tả chi tiết trên trang truyền tin.
Gọi
Xem thêm XlaBuilder::Call.
Gọi một phép tính với các đối số đã cho.
Call(computation, args...)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
computation |
XlaComputation |
tính toán loại T_0, T_1, ..., T_{N-1} -> S với N tham số thuộc loại tuỳ ý |
args |
trình tự của N XlaOp |
N đối số thuộc loại tuỳ ý |
Số lượng và loại của args phải khớp với các tham số của computation. Bạn có thể không có args.
Cholesky
Xem thêm XlaBuilder::Cholesky.
Tính toán phân ly Cholesky của một loạt ma trận đối xứng (Hermitian) dương xác định.
Cholesky(a, lower)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
a |
XlaOp |
một mảng có thứ hạng > 2 thuộc loại phức hoặc dấu phẩy động. |
lower |
bool |
liệu có nên sử dụng tam giác trên hay dưới của a. |
Nếu lower là true, hãy tính toán các ma trận tam giác dưới l sao cho . Nếu lower là false, hãy tính các ma trận tam giác trên u sao cho.
Dữ liệu đầu vào chỉ được đọc từ tam giác dưới/trên của a, tuỳ thuộc vào giá trị của lower. Các giá trị từ tam giác còn lại sẽ bị bỏ qua. Dữ liệu đầu ra được trả về trong cùng một tam giác; các giá trị trong tam giác còn lại được xác định bằng cách triển khai và có thể là bất kỳ giá trị nào.
Nếu thứ hạng của a lớn hơn 2, thì a sẽ được coi là một lô ma trận, trong đó tất cả ngoại trừ 2 chiều nhỏ là các chiều của lô.
Nếu a không phải là đối xứng (Hermitian) dương xác định, kết quả sẽ được xác định bằng cách triển khai.
Kẹp
Xem thêm XlaBuilder::Clamp.
Kẹp một toán hạng trong phạm vi giữa giá trị tối thiểu và tối đa.
Clamp(min, operand, max)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
min |
XlaOp |
mảng thuộc loại T |
operand |
XlaOp |
mảng thuộc loại T |
max |
XlaOp |
mảng thuộc loại T |
Cho một toán hạng và các giá trị tối thiểu và tối đa, trả về toán hạng nếu toán hạng đó nằm trong phạm vi giữa giá trị tối thiểu và tối đa, nếu không thì trả về giá trị tối thiểu nếu toán hạng nằm dưới phạm vi này hoặc giá trị tối đa nếu toán hạng nằm trên phạm vi này. Đó là clamp(a, x, b) = min(max(a, x), b).
Cả ba mảng phải có cùng hình dạng. Ngoài ra, dưới dạng một hình thức truyền tin bị hạn chế, min và/hoặc max có thể là một đại lượng vô hướng thuộc loại T.
Ví dụ với min và max vô hướng:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
Thu gọn
Hãy xem thêm
XlaBuilder::Collapse
và toán tử tf.reshape.
Thu gọn các phương diện của một mảng thành một phương diện.
Collapse(operand, dimensions)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
mảng thuộc loại T |
dimensions |
Vectơ int64 |
theo thứ tự, là tập con liên tiếp của các chiều T. |
Thao tác thu gọn sẽ thay thế tập hợp con đã cho của các phương diện của toán hạng bằng một phương diện duy nhất. Các đối số đầu vào là một mảng tuỳ ý thuộc loại T và một vectơ hằng thời gian biên dịch của các chỉ mục kích thước. Chỉ mục kích thước phải là một tập hợp con liên tiếp theo thứ tự (số kích thước từ thấp đến cao) của các kích thước của T. Do đó, {0, 1, 2}, {0, 1} hoặc {1, 2} đều là các tập hợp thứ nguyên hợp lệ, nhưng {1, 0} hoặc {0, 2} thì không. Các phương diện này được thay thế bằng một phương diện mới, ở cùng vị trí trong trình tự phương diện như các phương diện mà chúng thay thế, với kích thước phương diện mới bằng tích của kích thước phương diện ban đầu. Số phương diện thấp nhất trong dimensions là phương diện thay đổi chậm nhất (chính nhất) trong lồng lặp thu gọn các phương diện này và số phương diện cao nhất là phương diện thay đổi nhanh nhất (phụ nhất). Xem toán tử tf.reshape nếu bạn cần thứ tự thu gọn chung hơn.
Ví dụ: giả sử v là một mảng gồm 24 phần tử:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
CollectivePermute
Xem thêm XlaBuilder::CollectivePermute.
CollectivePermute là một thao tác tập thể gửi và nhận dữ liệu giữa các bản sao.
CollectivePermute(operand, source_target_pairs)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng đầu vào n chiều |
source_target_pairs |
Vectơ <int64, int64> |
Danh sách các cặp (source_replica_id, target_replica_id). Đối với mỗi cặp, toán hạng được gửi từ bản sao nguồn đến bản sao đích. |
Xin lưu ý rằng có các hạn chế sau đây đối với source_target_pair:
- Hai cặp bất kỳ không được có cùng mã bản sao mục tiêu và không nên có cùng mã bản sao nguồn.
- Nếu mã bản sao không phải là mục tiêu trong bất kỳ cặp nào, thì đầu ra trên bản sao đó là một tensor bao gồm 0(s) có cùng hình dạng với đầu vào.
Nối
Xem thêm XlaBuilder::ConcatInDim.
Hàm liên kết sẽ tạo một mảng từ nhiều toán hạng mảng. Mảng này có cùng thứ hạng với từng toán hạng mảng đầu vào (phải có cùng thứ hạng với nhau) và chứa các đối số theo thứ tự được chỉ định.
Concatenate(operands..., dimension)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operands |
trình tự của N XlaOp |
N mảng thuộc loại T có kích thước [L0, L1, ...]. Yêu cầu N >= 1. |
dimension |
int64 |
Một giá trị trong khoảng [0, N) đặt tên cho phương diện cần nối giữa operands. |
Ngoại trừ dimension, tất cả các phương diện phải giống nhau. Điều này là do XLA không hỗ trợ các mảng "phân mảnh". Ngoài ra, xin lưu ý rằng các giá trị thứ hạng 0 không thể nối với nhau (vì không thể đặt tên cho chiều mà quá trình nối diễn ra cùng với thứ nguyên đó).
Ví dụ về 1 chiều:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
>>> {2, 3, 4, 5, 6, 7}
Ví dụ về 2 chiều:
let a = {
{1, 2},
{3, 4},
{5, 6},
};
let b = {
{7, 8},
};
Concat({a, b}, 0)
>>> {
{1, 2},
{3, 4},
{5, 6},
{7, 8},
}
Sơ đồ:
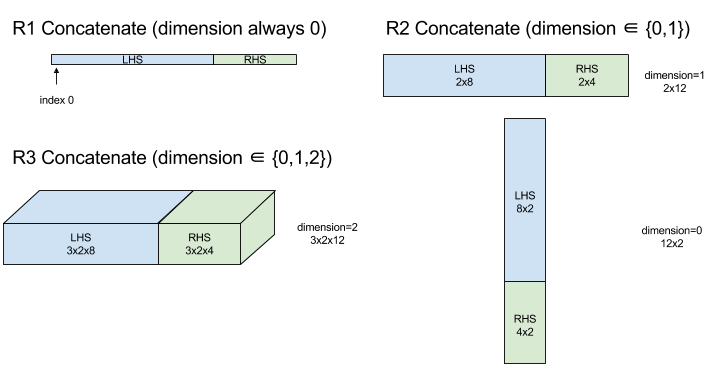
Câu lệnh có điều kiện
Xem thêm XlaBuilder::Conditional.
Conditional(pred, true_operand, true_computation, false_operand,
false_computation)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
pred |
XlaOp |
Số thực thuộc loại PRED |
true_operand |
XlaOp |
Đối số thuộc loại |
true_computation |
XlaComputation |
XlaComputation thuộc loại |
false_operand |
XlaOp |
Đối số thuộc loại |
false_computation |
XlaComputation |
XlaComputation thuộc loại |
Thực thi true_computation nếu pred là true, false_computation nếu pred là false và trả về kết quả.
true_computation phải nhận một đối số duy nhất thuộc loại và sẽ được gọi bằng true_operand phải thuộc cùng loại. false_computation phải nhận một đối số duy nhất thuộc loại và sẽ được gọi bằng false_operand phải thuộc cùng loại. Loại của giá trị trả về của true_computation và false_computation phải giống nhau.
Xin lưu ý rằng chỉ một trong hai giá trị true_computation và false_computation sẽ được thực thi tuỳ thuộc vào giá trị của pred.
Conditional(branch_index, branch_computations, branch_operands)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
branch_index |
XlaOp |
Số thực thuộc loại S32 |
branch_computations |
chuỗi của N XlaComputation |
XlaComputations thuộc loại |
branch_operands |
trình tự của N XlaOp |
Đối số thuộc loại |
Thực thi branch_computations[branch_index] và trả về kết quả. Nếu branch_index là một S32 < 0 hoặc >= N, thì branch_computations[N-1] sẽ được thực thi dưới dạng nhánh mặc định.
Mỗi branch_computations[b] phải nhận một đối số duy nhất thuộc loại và sẽ được gọi bằng branch_operands[b] phải thuộc cùng loại. Loại giá trị trả về của mỗi branch_computations[b] phải giống nhau.
Xin lưu ý rằng chỉ một trong branch_computations sẽ được thực thi tuỳ thuộc vào giá trị của branch_index.
Conv (tích chập)
Xem thêm XlaBuilder::Conv.
Là ConvWithGeneralPadding, nhưng khoảng đệm được chỉ định theo cách ngắn gọn là SAME hoặc VALID. SAME đệm dữ liệu đầu vào (lhs) bằng số 0 để đầu ra có cùng hình dạng với dữ liệu đầu vào khi không tính đến bước. Khoảng đệm VALID (CHÍNH THỨC) đơn giản có nghĩa là không có khoảng đệm.
ConvWithGeneralPadding (tích chập)
Xem thêm XlaBuilder::ConvWithGeneralPadding.
Tính toán một tích chập loại dùng trong mạng nơron. Ở đây, phép tích chập có thể được coi là một cửa sổ n chiều di chuyển trên một vùng cơ sở n chiều và một phép tính được thực hiện cho mỗi vị trí có thể có của cửa sổ.
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
lhs |
XlaOp |
thứ hạng n+2 mảng dữ liệu đầu vào |
rhs |
XlaOp |
mảng thứ hạng n+2 của trọng số hạt nhân |
window_strides |
ArraySlice<int64> |
Mảng n-d của bước nhân |
padding |
ArraySlice< pair<int64,int64>> |
Mảng n-d của khoảng đệm (thấp, cao) |
lhs_dilation |
ArraySlice<int64> |
mảng hệ số giãn nở lhs n-d |
rhs_dilation |
ArraySlice<int64> |
mảng hệ số giãn nở bên phải n-d |
feature_group_count |
int64 | số lượng nhóm tính năng |
batch_group_count |
int64 | số lượng nhóm theo lô |
Gọi n là số chiều không gian. Đối số lhs là một mảng thứ hạng n+2 mô tả diện tích cơ sở. Đây được gọi là dữ liệu đầu vào, mặc dù tất nhiên bên phải cũng là dữ liệu đầu vào. Trong mạng nơron, đây là các hoạt động kích hoạt đầu vào.
Các phương diện n+2 theo thứ tự như sau:
batch: Mỗi toạ độ trong chiều này đại diện cho một đầu vào độc lập có thể thực hiện phép tích chập.z/depth/features: Mỗi vị trí (y,x) trong vùng cơ sở đều có một vectơ liên kết với vị trí đó, vectơ này sẽ đi vào phương diện này.spatial_dims: Mô tả các kích thước không giannxác định vùng cơ sở mà cửa sổ di chuyển qua.
Đối số rhs là một mảng thứ hạng n+2 mô tả bộ lọc tích chập/hạt nhân/cửa sổ. Các phương diện theo thứ tự sau đây:
output-z: Phương diệnzcủa đầu ra.input-z: Kích thước của phương diện này nhân vớifeature_group_countphải bằng kích thước của phương diệnztrong lhs.spatial_dims: Mô tả các kích thước không giannxác định cửa sổ n-d di chuyển trên khu vực cơ sở.
Đối số window_strides chỉ định bước của cửa sổ tích chập trong các kích thước không gian. Ví dụ: nếu bước trong kích thước không gian đầu tiên là 3, thì cửa sổ chỉ có thể được đặt ở các toạ độ mà chỉ mục không gian đầu tiên có thể chia hết cho 3.
Đối số padding chỉ định khoảng đệm bằng 0 sẽ được áp dụng cho vùng cơ sở. Số lượng khoảng đệm có thể là số âm -- giá trị tuyệt đối của khoảng đệm âm cho biết số phần tử cần xoá khỏi phương diện được chỉ định trước khi thực hiện tích chập. padding[0] chỉ định khoảng đệm cho phương diện y và padding[1] chỉ định khoảng đệm cho phương diện x. Mỗi cặp có khoảng đệm thấp làm phần tử đầu tiên và khoảng đệm cao làm phần tử thứ hai. Khoảng đệm thấp được áp dụng theo hướng của chỉ mục thấp hơn, trong khi khoảng đệm cao được áp dụng theo hướng của chỉ mục cao hơn. Ví dụ: nếu padding[1] là (2,3), thì sẽ có khoảng đệm là 2 số 0 ở bên trái và 3 số 0 ở bên phải trong phương diện không gian thứ hai. Việc sử dụng khoảng đệm tương đương với việc chèn chính các giá trị 0 đó vào dữ liệu đầu vào (lhs) trước khi thực hiện phép tích chập.
Các đối số lhs_dilation và rhs_dilation chỉ định hệ số giãn nở sẽ được áp dụng cho lhs và rhs tương ứng trong mỗi kích thước không gian. Nếu hệ số giãn nở trong một kích thước không gian là d, thì các lỗ d-1 sẽ được ngầm đặt giữa từng phần tử trong kích thước đó, làm tăng kích thước của mảng. Các lỗ được lấp đầy bằng giá trị không hoạt động, giá trị tích chập có nghĩa là giá trị bằng 0.
Việc mở rộng bên phải cũng được gọi là phép tích chập atrous. Để biết thêm thông tin, hãy xem tf.nn.atrous_conv2d. Việc mở rộng lhs còn được gọi là phép tích chập chuyển đổi. Để biết thêm thông tin, hãy xem tf.nn.conv2d_transpose.
Bạn có thể sử dụng đối số feature_group_count (giá trị mặc định là 1) cho các phép tích chập được nhóm. feature_group_count cần là bộ chia của cả phương diện đầu vào và đầu ra. Nếu feature_group_count lớn hơn 1, thì điều này có nghĩa là về mặt khái niệm, kích thước đặc điểm đầu vào và đầu ra cũng như kích thước đặc điểm đầu ra rhs được chia đều thành nhiều nhóm feature_group_count, mỗi nhóm bao gồm một chuỗi con liên tiếp của các đặc điểm. Phương diện đặc điểm đầu vào của rhs cần bằng phương diện đặc điểm đầu vào lhs chia cho feature_group_count (vì vậy, phương diện này đã có kích thước của một nhóm đặc điểm đầu vào). Các nhóm thứ i được dùng cùng nhau để tính toán
feature_group_count cho nhiều phép tích chập riêng biệt. Kết quả của các phép tích chập này được nối với nhau trong phương diện đặc điểm đầu ra.
Đối với tích chập theo chiều sâu, đối số feature_group_count sẽ được đặt thành phương diện tính năng đầu vào và bộ lọc sẽ được định hình lại từ [filter_height, filter_width, in_channels, channel_multiplier] thành [filter_height, filter_width, 1, in_channels * channel_multiplier]. Để biết thêm thông tin chi tiết, hãy xem tf.nn.depthwise_conv2d.
Bạn có thể sử dụng đối số batch_group_count (giá trị mặc định là 1) cho các bộ lọc được nhóm trong quá trình truyền ngược. batch_group_count cần là bộ chia của kích thước nhóm lhs (dữ liệu đầu vào). Nếu batch_group_count lớn hơn 1, thì kích thước lô đầu ra phải là input batch
/ batch_group_count. batch_group_count phải là bộ chia của kích thước đặc điểm đầu ra.
Hình dạng đầu ra có các kích thước sau, theo thứ tự sau:
batch: Kích thước của phương diện này nhân vớibatch_group_countphải bằng kích thước của phương diệnbatchtrong lhs.z: Có cùng kích thước vớioutput-ztrên hạt nhân (rhs).spatial_dims: Một giá trị cho mỗi vị trí hợp lệ của cửa sổ tích chập.
Hình trên cho thấy cách hoạt động của trường batch_group_count. Một cách hiệu quả, chúng tôi cắt từng lô lhs thành các nhóm batch_group_count và làm tương tự cho các tính năng đầu ra. Sau đó, đối với mỗi nhóm này, chúng ta thực hiện phép tích chập từng cặp và nối kết quả theo chiều kích thước đặc điểm đầu ra. Ngữ nghĩa hoạt động của tất cả các phương diện khác (tính năng và không gian) vẫn giữ nguyên.
Vị trí hợp lệ của cửa sổ tích chập được xác định bằng bước và kích thước của vùng cơ sở sau khi thêm khoảng đệm.
Để mô tả chức năng của phép tích chập, hãy xem xét phép tích chập 2D và chọn một số tọa độ batch, z, y, x cố định trong kết quả. Sau đó, (y,x) là vị trí của một góc cửa sổ trong khu vực cơ sở (ví dụ: góc trên bên trái, tuỳ thuộc vào cách bạn diễn giải các kích thước không gian). Bây giờ, chúng ta có một cửa sổ 2D, lấy từ vùng cơ sở, trong đó mỗi điểm 2D được liên kết với một vectơ 1D, vì vậy, chúng ta có một hộp 3D. Từ hạt nhân tích chập, vì đã cố định hệ toạ độ đầu ra z, nên chúng ta cũng có một hộp 3D. Hai hộp có cùng kích thước, vì vậy, chúng ta có thể lấy tổng tích theo phần tử giữa hai hộp (tương tự như tích vô hướng). Đó là giá trị đầu ra.
Lưu ý rằng nếu output-z là, ví dụ: 5, thì mỗi vị trí của cửa sổ sẽ tạo ra 5 giá trị trong đầu ra vào phương diện z của đầu ra. Các giá trị này khác nhau về phần hạt nhân tích luỹ được sử dụng – có một hộp 3D riêng biệt của các giá trị được sử dụng cho mỗi toạ độ output-z. Vì vậy, bạn có thể xem đây là 5 tích chập riêng biệt với một bộ lọc khác nhau cho mỗi tích chập.
Dưới đây là mã giả cho tích chập 2d có khoảng đệm và sải chân:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
ConvertElementType
Xem thêm XlaBuilder::ConvertElementType.
Tương tự như static_cast phân loại phần tử trong C++, thực hiện thao tác chuyển đổi phần tử thông minh từ hình dạng dữ liệu sang hình dạng mục tiêu. Các phương diện phải khớp và lượt chuyển đổi là một lượt chuyển đổi theo phần tử; ví dụ: các phần tử s32 trở thành các phần tử f32 thông qua một quy trình chuyển đổi s32 sang f32.
ConvertElementType(operand, new_element_type)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
mảng thuộc loại T với kích thước D |
new_element_type |
PrimitiveType |
loại U |
Phương diện của toán hạng và hình dạng đích phải khớp nhau. Loại phần tử nguồn và đích không được là các bộ đôi.
Một lượt chuyển đổi như T=s32 sang U=f32 sẽ thực hiện một quy trình chuyển đổi số nguyên sang số thực chuẩn hoá, chẳng hạn như làm tròn đến số chẵn gần nhất.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
CrossReplicaSum
Thực hiện AllReduce bằng phép tính tổng.
CustomCall
Xem thêm XlaBuilder::CustomCall.
Gọi một hàm do người dùng cung cấp trong một phép tính.
CustomCall(target_name, args..., shape)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
target_name |
string |
Tên hàm. Hệ thống sẽ phát một lệnh gọi nhắm đến tên ký hiệu này. |
args |
trình tự của N XlaOp |
N đối số thuộc loại tuỳ ý sẽ được truyền vào hàm. |
shape |
Shape |
Hình dạng đầu ra của hàm |
Chữ ký hàm giống nhau, bất kể đối số hay loại đối số:
extern "C" void target_name(void* out, void** in);
Ví dụ: nếu CustomCall được sử dụng như sau:
let x = f32[2] {1,2};
let y = f32[2x3] { {10, 20, 30}, {40, 50, 60} };
CustomCall("myfunc", {x, y}, f32[3x3])
Dưới đây là ví dụ về cách triển khai myfunc:
extern "C" void myfunc(void* out, void** in) {
float (&x)[2] = *static_cast<float(*)[2]>(in[0]);
float (&y)[2][3] = *static_cast<float(*)[2][3]>(in[1]);
EXPECT_EQ(1, x[0]);
EXPECT_EQ(2, x[1]);
EXPECT_EQ(10, y[0][0]);
EXPECT_EQ(20, y[0][1]);
EXPECT_EQ(30, y[0][2]);
EXPECT_EQ(40, y[1][0]);
EXPECT_EQ(50, y[1][1]);
EXPECT_EQ(60, y[1][2]);
float (&z)[3][3] = *static_cast<float(*)[3][3]>(out);
z[0][0] = x[1] + y[1][0];
// ...
}
Hàm do người dùng cung cấp không được có tác dụng phụ và quá trình thực thi phải không thay đổi.
Chấm
Hãy xem thêm XlaBuilder::Dot.
Dot(lhs, rhs)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
lhs |
XlaOp |
mảng thuộc loại T |
rhs |
XlaOp |
mảng thuộc loại T |
Ngữ nghĩa chính xác của toán tử này phụ thuộc vào thứ hạng của các toán hạng:
| Đầu vào | Đầu ra | Ngữ nghĩa |
|---|---|---|
vectơ [n] dot vectơ [n] |
đại lượng vô hướng | tích vô hướng của vectơ |
ma trận [m x k] vectơ dot [k] |
vectơ [m] | phép nhân vectơ của ma trận |
ma trận [m x k] dot ma trận [k x n] |
ma trận [m x n] | phép nhân ma trận màu |
Toán tử này thực hiện phép tính tổng tích trên phương diện thứ hai của lhs (hoặc phương diện đầu tiên nếu có thứ hạng 1) và phương diện đầu tiên của rhs. Đây là các kích thước "có hợp đồng". Kích thước rút gọn của lhs và rhs phải có cùng kích thước. Trong thực tế, bạn có thể dùng hàm này để thực hiện phép nhân dấu chấm giữa các vectơ, phép nhân vectơ/ma trận hoặc phép nhân ma trận/ma trận.
DotGeneral
Xem thêm XlaBuilder::DotGeneral.
DotGeneral(lhs, rhs, dimension_numbers)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
lhs |
XlaOp |
mảng thuộc loại T |
rhs |
XlaOp |
mảng thuộc loại T |
dimension_numbers |
DotDimensionNumbers |
số thứ nguyên hợp đồng và số thứ nguyên lô |
Tương tự như Dot, nhưng cho phép chỉ định số thứ nguyên theo lô và thu hẹp cho cả lhs và rhs.
| Trường DotDimensionNumbers | Loại | Ngữ nghĩa |
|---|---|---|
lhs_contracting_dimensions
|
int64 lặp lại | lhs số kích thước theo hợp đồng |
rhs_contracting_dimensions
|
int64 lặp lại | rhs số phương diện rút gọn |
lhs_batch_dimensions
|
int64 lặp lại | lhs số phương diện lô |
rhs_batch_dimensions
|
int64 lặp lại | rhs số kích thước theo lô |
DotGeneral thực hiện phép tính tổng các tích trên các phương diện hợp đồng được chỉ định trong dimension_numbers.
Các số kích thước hợp đồng liên kết từ lhs và rhs không cần phải giống nhau nhưng phải có cùng kích thước kích thước.
Ví dụ về số kích thước theo hợp đồng:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { {6.0, 12.0},
{15.0, 30.0} }
Các số phương diện lô được liên kết từ lhs và rhs phải có cùng kích thước phương diện.
Ví dụ về số lượng phương diện theo lô (kích thước lô 2, ma trận 2x2):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| Đầu vào | Đầu ra | Ngữ nghĩa |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | matmul hàng loạt |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | matmul hàng loạt |
Do đó, số phương diện thu được sẽ bắt đầu bằng phương diện theo lô, sau đó là phương diện không hợp đồng/không theo lô lhs và cuối cùng là phương diện không hợp đồng/không theo lô rhs.
DynamicSlice
Xem thêm XlaBuilder::DynamicSlice.
DynamicSlice trích xuất một mảng con từ mảng đầu vào tại start_indices động. Kích thước của lát cắt trong mỗi chiều được truyền vào size_indices, mã này chỉ định điểm cuối của các khoảng lát cắt loại trừ trong mỗi chiều: [bắt đầu, bắt đầu + kích thước). Hình dạng của start_indices phải là thứ hạng == 1, với kích thước thứ nguyên bằng thứ hạng của operand.
DynamicSlice(operand, start_indices, size_indices)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng N chiều thuộc loại T |
start_indices |
trình tự của N XlaOp |
Danh sách các số nguyên vô hướng N chứa các chỉ mục bắt đầu của lát cắt cho mỗi phương diện. Giá trị phải lớn hơn hoặc bằng 0. |
size_indices |
ArraySlice<int64> |
Danh sách N số nguyên chứa kích thước lát cắt cho mỗi phương diện. Mỗi giá trị phải lớn hơn 0 và start + size phải nhỏ hơn hoặc bằng kích thước của phương diện để tránh gói kích thước phương diện theo modulo. |
Các chỉ mục lát cắt hiệu quả được tính toán bằng cách áp dụng phép biến đổi sau cho mỗi chỉ mục i trong [1, N) trước khi thực hiện lát cắt:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - size_indices[i])
Điều này đảm bảo rằng lát cắt được trích xuất luôn nằm trong giới hạn so với mảng toán hạng. Nếu lát cắt nằm trong giới hạn trước khi áp dụng phép biến đổi, thì phép biến đổi sẽ không có hiệu lực.
Ví dụ về 1 chiều:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let s = {2}
DynamicSlice(a, s, {2}) produces:
{2.0, 3.0}
Ví dụ 2 chiều:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2}) produces:
{ { 7.0, 8.0},
{10.0, 11.0} }
DynamicUpdateSlice
Xem thêm XlaBuilder::DynamicUpdateSlice.
DynamicUpdateSlice tạo ra một kết quả là giá trị của mảng đầu vào operand, với một lát cắt update được ghi đè tại start_indices.
Hình dạng của update xác định hình dạng của mảng con của kết quả được cập nhật.
Hình dạng của start_indices phải có thứ hạng == 1, với kích thước kích thước bằng thứ hạng của operand.
DynamicUpdateSlice(operand, update, start_indices)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng N chiều thuộc loại T |
update |
XlaOp |
Mảng N chiều thuộc loại T chứa nội dung cập nhật lát cắt. Mỗi phương diện của hình dạng cập nhật phải lớn hơn 0 và start + update phải nhỏ hơn hoặc bằng kích thước toán hạng cho mỗi phương diện để tránh tạo chỉ mục cập nhật ngoài giới hạn. |
start_indices |
chuỗi của N XlaOp |
Danh sách các số nguyên vô hướng N chứa các chỉ mục bắt đầu của lát cắt cho mỗi phương diện. Giá trị phải lớn hơn hoặc bằng 0. |
Các chỉ mục lát cắt hiệu quả được tính toán bằng cách áp dụng phép biến đổi sau cho mỗi chỉ mục i trong [1, N) trước khi thực hiện lát cắt:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
Điều này đảm bảo rằng lát cắt đã cập nhật luôn nằm trong giới hạn so với mảng toán hạng. Nếu lát cắt nằm trong giới hạn trước khi áp dụng phép biến đổi, thì phép biến đổi sẽ không có hiệu lực.
Ví dụ về 1 chiều:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s) produces:
{0.0, 1.0, 5.0, 6.0, 4.0}
Ví dụ 2 chiều:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s) produces:
{ {0.0, 1.0, 2.0},
{3.0, 12.0, 13.0},
{6.0, 14.0, 15.0},
{9.0, 16.0, 17.0} }
Phép tính số học nhị phân trên các phần tử
Xem thêm XlaBuilder::Add.
Một tập hợp các phép tính số học nhị phân xuất hiện trên cùng một phần tử được hỗ trợ.
Op(lhs, rhs)
Trong đó Op là một trong các giá trị Add (cộng), Sub (phép cộng), Mul (nhân), Div (phép chia), Pow ( luỹ thừa), Rem (số dư), Max (tối đa), Min (tối thiểu), And (logic AND), Or (hàm tổng hợp), Xor (logic XOR), ShiftLeft (Shift trái), ShiftRightArithmetic (số phức/số phức}, ShiftRightLogical (số phức)Atan2Complex
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
lhs |
XlaOp |
toán hạng bên trái: mảng thuộc kiểu T |
rhs |
XlaOp |
toán hạng bên phải: mảng thuộc loại T |
Hình dạng của các đối số phải tương tự hoặc tương thích. Hãy xem tài liệu về truyền tin để biết ý nghĩa của việc các hình dạng tương thích với nhau. Kết quả của một thao tác có hình dạng là kết quả của việc truyền 2 mảng đầu vào. Trong biến thể này, các phép toán giữa các mảng có thứ hạng khác nhau không được hỗ trợ, trừ phi một trong các toán hạng là một đại lượng vô hướng.
Khi Op là Rem, dấu của kết quả được lấy từ số bị chia và giá trị tuyệt đối của kết quả luôn nhỏ hơn giá trị tuyệt đối của số chia.
tràn số nguyên (phân chia có dấu/chưa ký/phần còn lại bằng 0 hoặc phép chia có dấu/phần còn lại của INT_SMIN với -1) tạo ra giá trị do phương thức triển khai xác định.
Có một biến thể thay thế có hỗ trợ truyền tin theo thứ hạng khác nhau cho các thao tác này:
Op(lhs, rhs, broadcast_dimensions)
Trong đó, Op giống như trên. Bạn nên sử dụng biến thể của toán tử này cho các phép toán số học giữa các mảng có thứ hạng khác nhau (chẳng hạn như thêm một ma trận vào một vectơ).
Toán hạng broadcast_dimensions bổ sung là một lát cắt số nguyên dùng để mở rộng thứ hạng của toán hạng có thứ hạng thấp hơn lên đến thứ hạng của toán hạng có thứ hạng cao hơn. broadcast_dimensions ánh xạ các kích thước của hình dạng cấp thấp hơn với các kích thước của hình dạng cấp cao hơn. Các kích thước chưa được liên kết của hình dạng mở rộng được lấp đầy bằng các kích thước có kích thước 1. Truyền phát chiều thoái hoá rồi truyền hình dạng theo các chiều suy giảm này để cân bằng hình dạng của cả hai toán hạng. Ngữ nghĩa được mô tả chi tiết trên trang truyền tin.
Thao tác so sánh các phần tử
Hãy xem thêm XlaBuilder::Eq.
Hỗ trợ một tập hợp các phép toán so sánh nhị phân chuẩn trên các phần tử. Xin lưu ý rằng ngữ nghĩa so sánh dấu phẩy động IEEE 754 tiêu chuẩn sẽ áp dụng khi so sánh các kiểu dấu phẩy động.
Op(lhs, rhs)
Trong đó Op là một trong các giá trị Eq (bằng), Ne (không bằng), Ge (lớn hơn hoặc bằng), Gt (lớn hơn), Le (nhỏ hơn hoặc bằng), Lt (nhỏ hơn). Một nhóm toán tử khác là EqTotalOrder, NeTotalOrder, GeTotalOrder, GtTotalOrder, LeTotalOrder và LtTotalOrder, cung cấp các chức năng tương tự, ngoại trừ việc chúng hỗ trợ bổ sung một tổng thứ tự trên các số dấu phẩy động, bằng cách thực thi -NaN < -Inf < -Finite < -0 < +0 < +Finite < +Na
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
lhs |
XlaOp |
toán hạng bên trái: mảng thuộc kiểu T |
rhs |
XlaOp |
toán hạng bên phải: mảng thuộc loại T |
Hình dạng của đối số phải tương tự hoặc tương thích. Hãy xem tài liệu về cách truyền tin về ý nghĩa của việc hình dạng trở nên tương thích. Kết quả của một phép toán có hình dạng là kết quả của việc truyền tin hai mảng đầu vào có kiểu phần tử PRED. Trong biến thể này, các thao tác giữa các mảng có thứ hạng khác nhau không được hỗ trợ, trừ phi một trong các toán hạng là một đại lượng vô hướng.
Hiện có một biến thể thay thế có hỗ trợ tính năng phát sóng theo thứ hạng khác cho các thao tác sau:
Op(lhs, rhs, broadcast_dimensions)
Trong đó Op giống như trên. Bạn nên sử dụng biến thể của toán tử này cho các phép toán so sánh giữa các mảng có thứ hạng khác nhau (chẳng hạn như thêm một ma trận vào một vectơ).
Toán hạng broadcast_dimensions bổ sung là một lát cắt của số nguyên chỉ định các phương diện để sử dụng cho việc truyền tin các toán hạng. Ngữ nghĩa được mô tả chi tiết trên trang truyền tin.
Hàm một ngôi theo phần tử
XlaBuilder hỗ trợ các hàm một ngôi theo phần tử sau:
Abs(operand) Bố cục tuyệt đối đa phần tử x -> |x|.
Cbrt(operand) Toán tử căn bậc ba của các phần tử x -> cbrt(x).
Ceil(operand) Cửa sổ phần tử x -> ⌈x⌉.
Clz(operand) Đếm số 0 ở đầu theo phần tử.
Cos(operand) Cosin cân bằng phần tử x -> cos(x).
Erf(operand) Hàm lỗi theo phần tử x -> erf(x), trong đó
.
Exp(operand) Exponent tự nhiên theo phần tử x -> e^x.
Expm1(operand) Số mũ tự nhiên tính theo phần tử trừ đi 1 x -> e^x - 1.
Floor(operand) Hàm lấy phần nguyên theo phần tử x -> ⌊x⌋.
Imag(operand) Phần ảo theo phần tử của một hình dạng phức (hoặc thực). x -> imag(x). Nếu toán hạng là kiểu dấu phẩy động, trả về 0.
IsFinite(operand) Kiểm tra xem mỗi phần tử của operand có hữu hạn hay không, nghĩa là không phải là vô cực dương hoặc âm và không phải là NaN. Trả về một mảng các giá trị PRED có cùng hình dạng với dữ liệu đầu vào, trong đó mỗi phần tử là true nếu và chỉ khi phần tử đầu vào tương ứng là hữu hạn.
Log(operand) Lôgarit tự nhiên theo phần tử x -> ln(x).
Log1p(operand) Lôgarit tự nhiên dịch chuyển theo phần tử x -> ln(1+x).
Logistic(operand) Tính toán hàm logistic theo phần tử x ->
logistic(x).
Neg(operand) Hàm phủ định phần tử x -> -x.
Not(operand) Phần tử logic không phải là x -> !(x).
PopulationCount(operand) Tính toán số bit được đặt trong mỗi phần tử của operand.
Real(operand) Phần thực theo phần tử của một hình dạng phức (hoặc thực).
x -> real(x). Nếu toán hạng là kiểu dấu phẩy động, trả về cùng một giá trị.
Round(operand) Làm tròn theo phần tử, các giá trị bằng nhau sẽ được làm tròn lên.
RoundNearestEven(operand) Làm tròn theo phần tử, liên kết với số chẵn gần nhất.
Rsqrt(operand) Hàm nghịch đảo trên các phần tử của phép toán căn bậc hai x -> 1.0 / sqrt(x).
Sign(operand) Toán tử ký hiệu phần tử x -> sgn(x) trong đó
bằng cách sử dụng toán tử so sánh của loại phần tử operand.
Sin(operand) Hình sin toàn phần x -> sin(x).
Sqrt(operand) Phép toán căn bậc hai phần tử x -> sqrt(x).
Tan(operand) Tangent theo phần tử x -> tan(x).
Tanh(operand) Tang hyperbol nguyên tố x -> tanh(x).
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Toán hạng của hàm |
Hàm này được áp dụng cho từng phần tử trong mảng operand, dẫn đến một mảng có cùng hình dạng. operand được phép là một đại lượng vô hướng (xếp hạng 0).
Fft
Thao tác XLA FFT sẽ triển khai Biến đổi Fourier tiến và nghịch đảo cho đầu vào/đầu ra thực và phức tạp. Hỗ trợ FFT nhiều chiều trên tối đa 3 trục.
Xem thêm XlaBuilder::Fft.
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng mà chúng ta đang biến đổi Fourier. |
fft_type |
FftType |
Hãy xem bảng bên dưới. |
fft_length |
ArraySlice<int64> |
Độ dài miền thời gian của các trục đang được biến đổi. Điều này đặc biệt cần thiết để IRFFT định cỡ đúng trục trong cùng, vì RFFT(fft_length=[16]) có cùng hình dạng đầu ra với RFFT(fft_length=[17]). |
FftType |
Ngữ nghĩa |
|---|---|
FFT |
Chuyển tiếp FFT phức-phức. Hình dạng không thay đổi. |
IFFT |
FFT từ phức tạp đến phức tạp ngược. Hình dạng không thay đổi. |
RFFT |
Chuyển tiếp FFT thực sang phức. Hình dạng của trục trong cùng giảm xuống còn fft_length[-1] // 2 + 1 nếu fft_length[-1] là một giá trị khác 0, bỏ qua phần liên hợp đảo ngược của tín hiệu biến đổi vượt quá tần số Nyquist. |
IRFFT |
Đảo ngược FFT từ thực đến phức (ví dụ: lấy phức, trả về thực). Hình dạng của trục trong cùng được mở rộng thành fft_length[-1] nếu fft_length[-1] là một giá trị khác 0, suy ra phần tín hiệu đã chuyển đổi ngoài tần số Nyquist từ số phức liên hợp đảo ngược của các mục 1 đến fft_length[-1] // 2 + 1. |
FFT đa chiều
Khi có nhiều fft_length được cung cấp, điều này tương đương với việc áp dụng một tầng gồm các thao tác FFT cho từng trục trong cùng. Xin lưu ý rằng đối với các trường hợp thực->phức tạp và phức tạp->thực, phép biến đổi trục trong cùng được thực hiện (một cách hiệu quả) trước tiên (RFFT; cuối cùng đối với IRFFT). Đó là lý do tại sao trục trong cùng là trục thay đổi kích thước. Các biến đổi trục khác sau đó sẽ phức tạp->phức tạp.
Thông tin chi tiết về cách triển khai
FFT CPU được hỗ trợ bởi TensorFFT của Eigen. GPU FFT sử dụng cuFFT.
Thu thập
Thao tác thu thập XLA sẽ ghép một số lát cắt lại với nhau (mỗi lát ở một độ lệch thời gian chạy có thể khác nhau) của một mảng đầu vào.
Ngữ nghĩa chung
Xem thêm XlaBuilder::Gather.
Để xem nội dung mô tả trực quan hơn, hãy xem phần "Mô tả không chính thức" bên dưới.
gather(operand, start_indices, offset_dims, collapsed_slice_dims, slice_sizes, start_index_map)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng mà chúng tôi đang thu thập. |
start_indices |
XlaOp |
Mảng chứa các chỉ mục bắt đầu của các lát cắt mà chúng tôi thu thập được. |
index_vector_dim |
int64 |
Phương diện trong start_indices "chứa" các chỉ mục bắt đầu. Hãy xem phần bên dưới để biết nội dung mô tả chi tiết. |
offset_dims |
ArraySlice<int64> |
Tập hợp các kích thước trong hình dạng đầu ra được bù vào một mảng được cắt từ toán hạng. |
slice_sizes |
ArraySlice<int64> |
slice_sizes[i] là giới hạn cho lát cắt trên phương diện i. |
collapsed_slice_dims |
ArraySlice<int64> |
Tập hợp các phương diện trong mỗi lát cắt đã bị thu gọn. Các phương diện này phải có kích thước 1. |
start_index_map |
ArraySlice<int64> |
Một bản đồ mô tả cách ánh xạ các chỉ mục trong start_indices đến các chỉ mục hợp lệ vào toán hạng. |
indices_are_sorted |
bool |
Liệu các chỉ mục có được đảm bảo là được sắp xếp theo phương thức gọi hay không. |
Để thuận tiện, chúng ta gắn nhãn các phương diện trong mảng đầu ra không phải trong offset_dims là batch_dims.
Kết quả là một mảng có thứ hạng batch_dims.size + offset_dims.size.
operand.rank phải bằng tổng của offset_dims.size và collapsed_slice_dims.size. Ngoài ra, slice_sizes.size phải bằng operand.rank.
Nếu index_vector_dim bằng start_indices.rank, chúng ta ngầm coi start_indices có kích thước 1 theo sau (tức là nếu start_indices có hình dạng [6,7] và index_vector_dim là 2, thì chúng ta ngầm coi hình dạng của start_indices là [6,7,1]).
Các giới hạn cho mảng đầu ra dọc theo phương diện i được tính như sau:
Nếu
icó trongbatch_dims(tức là bằngbatch_dims[k]đối với một sốk), thì chúng ta sẽ chọn các giới hạn phương diện tương ứng trongstart_indices.shape, bỏ quaindex_vector_dim(tức là chọnstart_indices.shape.dims[k] nếuk<index_vector_dimvàstart_indices.shape.dims[k+1] nếu không).Nếu
icó trongoffset_dims(tức là bằngoffset_dims[k] đối với một sốk), thì chúng ta sẽ chọn giới hạn tương ứng trongslice_sizessau khi tính đếncollapsed_slice_dims(tức là chúng ta chọnadjusted_slice_sizes[k] trong đóadjusted_slice_sizeslàslice_sizesđã xoá các giới hạn tại chỉ mụccollapsed_slice_dims).
Về mặt chính thức, chỉ mục toán hạng In tương ứng với một chỉ mục đầu ra nhất định Out được tính như sau:
Đặt
G= {Out[k] choktrongbatch_dims}. Sử dụngGđể cắt một vectơSsao choS[i] =start_indices[Combine(G,i)] trong đó Combine(A, b) chèn b vào vị tríindex_vector_dimvào A. Xin lưu ý rằng giá trị này được xác định rõ ràng ngay cả khiGtrống: NếuGtrống thìS=start_indices.Tạo chỉ mục bắt đầu,
Sin, vàooperandbằng cách sử dụngSbằng cách phân tánSbằngstart_index_map. Chính xác hơn:Sin[start_index_map[k]] =S[k] nếuk<start_index_map.size.Sin[_] =0.
Tạo một chỉ mục
Oinvàooperandbằng cách phân tán các chỉ mục tại các phương diện chênh lệch trongOuttheo tập hợpcollapsed_slice_dims. Chính xác hơn:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] nếuk<offset_dims.size(remapped_offset_dimsđược xác định bên dưới).Oin[_] =0nếu không.
InlàOin+Sin, trong đó + là phép bổ sung phần tử.
remapped_offset_dims là một hàm đơn điệu có miền [0,
offset_dims.size) và dải ô [0, operand.rank) \ collapsed_slice_dims. Nếu, ví dụ: offset_dims.size là 4, operand.rank là 6 và collapsed_slice_dims là {0, 2}, sau đó remapped_offset_dims là {0→1,
1→3, 2→4, 3→5}.
Nếu bạn đặt indices_are_sorted thành true, thì XLA có thể giả định rằng start_indices được người dùng sắp xếp (theo thứ tự tăng dần, sau khi phân tán các giá trị theo start_index_map). Nếu không, ngữ nghĩa sẽ được xác định bằng cách triển khai.
Nội dung mô tả và ví dụ thân thiện
Một cách dễ hiểu, mỗi chỉ mục Out trong mảng đầu ra tương ứng với một phần tử E trong mảng toán hạng, được tính như sau:
Chúng ta sử dụng các phương diện lô trong
Outđể tra cứu chỉ mục bắt đầu từstart_indices.Chúng ta sử dụng
start_index_mapđể ánh xạ chỉ mục bắt đầu (có kích thước có thể nhỏ hơn operand.rank) đến một chỉ mục bắt đầu "đầy đủ" vàooperand.Chúng tôi sẽ cắt một lát cắt động có kích thước
slice_sizesbằng cách sử dụng chỉ mục khởi động đầy đủ.Chúng ta định hình lại lát cắt bằng cách thu gọn các phương diện
collapsed_slice_dims. Vì tất cả các phương diện lát cắt đã thu gọn phải có giới hạn là 1, nên việc định hình lại này luôn hợp lệ.Chúng ta sử dụng các phương diện chênh lệch trong
Outđể lập chỉ mục vào lát cắt này nhằm lấy phần tử đầu vàoEtương ứng với chỉ mục đầu raOut.
index_vector_dim được đặt thành start_indices.rank – 1 trong tất cả các ví dụ sau. Các giá trị thú vị hơn cho index_vector_dim không thay đổi cơ bản hoạt động, nhưng làm cho cách trình bày hình ảnh trở nên cồng kềnh hơn.
Để hiểu rõ cách tất cả các phần trên khớp với nhau, hãy xem một ví dụ về việc thu thập 5 lát cắt của hình dạng [8,6] từ một mảng [16,11]. Vị trí của một lát cắt trong mảng [16,11] có thể được biểu thị dưới dạng vectơ chỉ mục có hình dạng S64[2], vì vậy, tập hợp 5 vị trí có thể được biểu thị dưới dạng mảng S64[5,2].
Sau đó, bạn có thể mô tả hành vi của toán tử thu thập dưới dạng một phép biến đổi chỉ mục lấy [G,O0,O1], một chỉ mục trong hình dạng đầu ra và ánh xạ chỉ mục đó đến một phần tử trong mảng đầu vào theo cách sau:
Trước tiên, chúng ta chọn một vectơ (X,Y) từ mảng chỉ mục thu thập bằng G.
Phần tử trong mảng đầu ra tại chỉ mục [G,O0,O1] sau đó là phần tử trong mảng đầu vào tại chỉ mục [X+O0,Y+O1].
slice_sizes là [8,6], quyết định phạm vi của O0 và O1, từ đó quyết định giới hạn của lát cắt.
Thao tác thu thập này hoạt động như một lát cắt động theo lô, trong đó G là phương diện nhóm.
Chỉ mục thu thập có thể là nhiều chiều. Ví dụ: phiên bản tổng quát hơn của ví dụ trên, sử dụng mảng "chỉ mục thu thập" có hình dạng [4,5,2] sẽ dịch các chỉ mục như sau:
Xin nhắc lại, đây là một lát cắt động theo lô G0 và G1 làm phương diện theo lô. Kích thước lát cắt vẫn là [8,6].
Toán tử thu thập trong XLA khái quát hoá ngữ nghĩa không chính thức được nêu ở trên theo các cách sau:
Chúng ta có thể định cấu hình những kích thước trong hình dạng đầu ra là kích thước bù (tham số chứa
O0,O1trong ví dụ cuối cùng). Các phương diện hàng loạt đầu ra (các phương diện chứaG0,G1trong ví dụ cuối) được xác định là các phương diện đầu ra không phải là các phương diện bù trừ.Số lượng phương diện chênh lệch đầu ra xuất hiện rõ ràng trong hình dạng đầu ra có thể nhỏ hơn thứ hạng đầu vào. Các chiều "bị thiếu" này (được liệt kê rõ ràng là
collapsed_slice_dims) phải có kích thước lát cắt là1. Vì có kích thước lát cắt là1nên chỉ mục hợp lệ duy nhất cho các lát cắt này là0và việc loại bỏ các lát cắt này không gây ra sự mơ hồ.Lát cắt được trích xuất từ mảng "Gather Indices" ("Thu thập chỉ mục") ((
X,Y) trong ví dụ cuối cùng) có thể có ít phần tử hơn thứ hạng mảng đầu vào và ánh xạ rõ ràng sẽ chỉ định cách mở rộng chỉ mục để có cùng thứ hạng với đầu vào.
Ví dụ cuối cùng, chúng tôi sử dụng (2) và (3) để triển khai tf.gather_nd:
G0 và G1 được dùng để cắt một chỉ mục bắt đầu khỏi mảng chỉ mục tập hợp như thường lệ, ngoại trừ chỉ mục bắt đầu chỉ có một phần tử là X. Tương tự, chỉ có một chỉ mục độ lệch đầu ra có giá trị O0. Tuy nhiên, trước khi được dùng làm chỉ mục vào mảng đầu vào, các chỉ mục này được mở rộng theo "Gather Index Mapping" (Tập hợp ánh xạ chỉ mục) (start_index_map trong nội dung mô tả chính thức) và "Offset Mapping" (Ánh xạ độ dời) (remapped_offset_dims trong nội dung mô tả chính thức) thành [X,0] và [0,O0] tương ứng, tổng cộng là [X,O0]. Nói cách khác, chỉ mục đầu ra [G0,G1,O0] ánh xạ đến chỉ mục đầu vào [GatherIndices[G0,G1,0],O0] cung cấp cho chúng ta ngữ nghĩa cho tf.gather_nd.
slice_sizes cho trường hợp này là [1,11]. Theo trực giác, điều này có nghĩa là mọi chỉ mục X trong mảng chỉ mục thu thập sẽ chọn toàn bộ một hàng và kết quả là chuỗi nối của tất cả các hàng này.
GetDimensionSize
Hãy xem thêm XlaBuilder::GetDimensionSize.
Trả về kích thước của phương diện đã cho của toán hạng. Toán hạng phải có hình dạng mảng.
GetDimensionSize(operand, dimension)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
mảng đầu vào n chiều |
dimension |
int64 |
Một giá trị trong khoảng [0, n) chỉ định phương diện |
SetDimensionSize
Xem thêm XlaBuilder::SetDimensionSize.
Đặt kích thước động của phương diện đã cho của XlaOp. Toán hạng phải có hình dạng mảng.
SetDimensionSize(operand, size, dimension)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng đầu vào n chiều. |
size |
XlaOp |
int32 đại diện cho kích thước động trong thời gian chạy. |
dimension |
int64 |
Một giá trị trong khoảng [0, n) chỉ định phương diện. |
Truyền toán hạng dưới dạng kết quả, với kích thước động do trình biên dịch theo dõi.
Các giá trị đệm sẽ bị hoạt động rút gọn ở hạ nguồn bỏ qua.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
GetTupleElement
Xem thêm XlaBuilder::GetTupleElement.
Lập chỉ mục vào một bộ dữ liệu có giá trị hằng số thời gian biên dịch.
Giá trị này phải là hằng số thời gian biên dịch để suy luận hình dạng có thể xác định loại giá trị thu được.
Mã này tương tự như std::get<int N>(t) trong C++. Về mặt lý thuyết:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
Xem thêm tf.tuple.
Nguồn cấp dữ liệu nội tuyến
Xem thêm XlaBuilder::Infeed.
Infeed(shape)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
shape |
Shape |
Hình dạng của dữ liệu được đọc từ giao diện Nguồn cấp dữ liệu. Bạn phải đặt trường bố cục của hình dạng sao cho khớp với bố cục của dữ liệu được gửi đến thiết bị; nếu không, hành vi của hình dạng sẽ không xác định. |
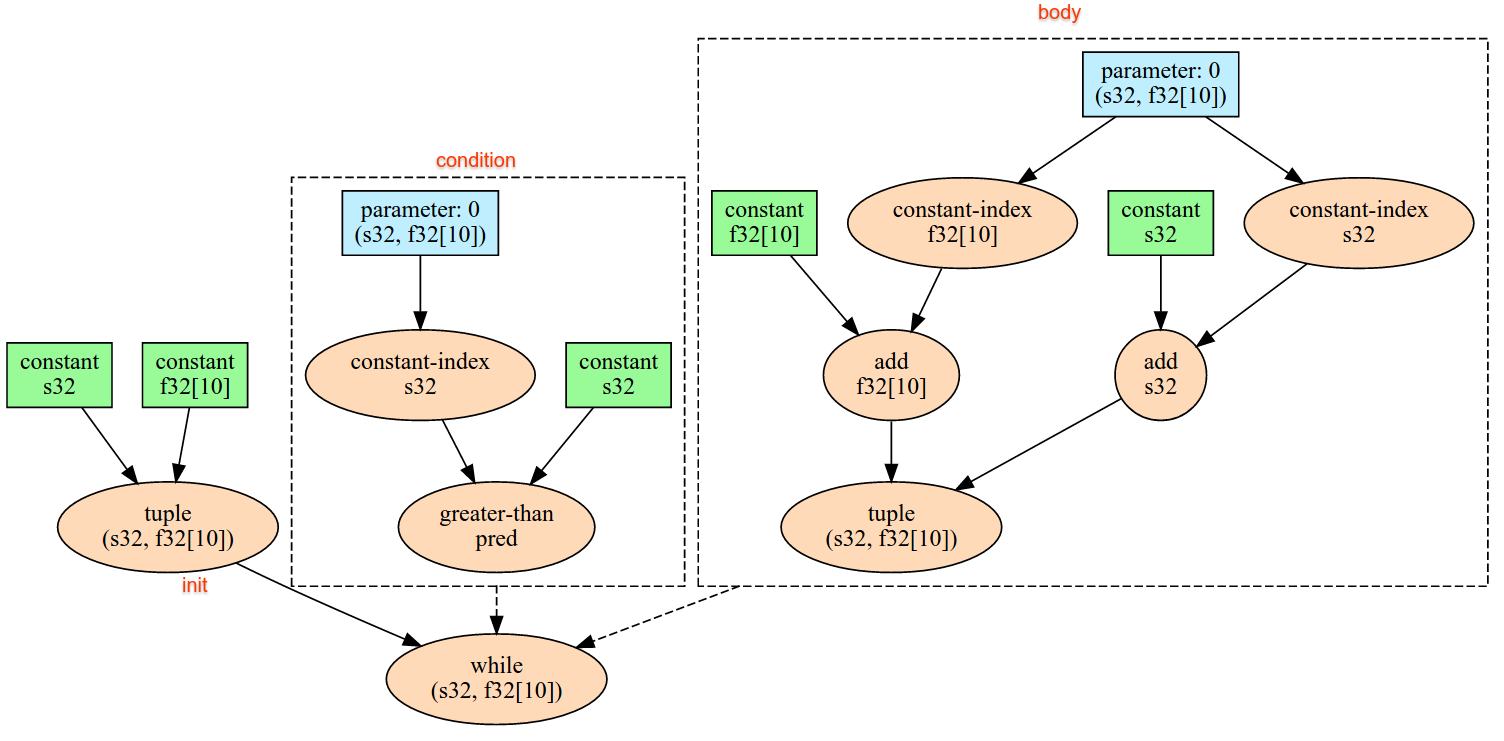
Đọc một mục dữ liệu duy nhất từ giao diện truyền trực tuyến trong nguồn cấp dữ liệu ngầm ẩn của thiết bị, diễn giải dữ liệu dưới dạng hình dạng và bố cục nhất định, đồng thời trả về XlaOp của dữ liệu. Bạn có thể thực hiện nhiều thao tác trong nguồn cấp dữ liệu trong quá trình tính toán, nhưng phải có tổng thứ tự giữa các thao tác trong nguồn cấp dữ liệu. Ví dụ: hai nguồn cấp dữ liệu trong mã bên dưới có tổng thứ tự vì có một phần phụ thuộc giữa các vòng lặp while.
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
Không hỗ trợ các hình dạng cặp lồng nhau. Đối với một hình dạng tuple trống, thao tác trong nguồn cấp dữ liệu sẽ không hoạt động và tiếp tục mà không cần đọc bất kỳ dữ liệu nào từ nguồn cấp dữ liệu của thiết bị.
Iôta
Xem thêm XlaBuilder::Iota.
Iota(shape, iota_dimension)
Tạo một hằng số cố định trên thiết bị thay vì một quá trình chuyển máy chủ có thể lớn. Tạo một mảng đã chỉ định hình dạng và giữ các giá trị bắt đầu từ 0 và tăng dần một giá trị dọc theo kích thước được chỉ định. Đối với các loại dấu phẩy động, mảng được tạo tương đương với ConvertElementType(Iota(...)), trong đó Iota thuộc loại số nguyên và quá trình chuyển đổi là sang loại dấu phẩy động.
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
shape |
Shape |
Hình dạng của mảng do Iota() tạo |
iota_dimension |
int64 |
Phương diện để tăng dần. |
Ví dụ: Iota(s32[4, 8], 0) trả về
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
Trả lại hàng với mức phí Iota(s32[4, 8], 1)
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
Bản đồ
Hãy xem thêm XlaBuilder::Map.
Map(operands..., computation)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operands |
trình tự của N XlaOp |
N mảng thuộc loại T0..T{N-1} |
computation |
XlaComputation |
tính toán loại T_0, T_1, .., T_{N + M -1} -> S với N tham số thuộc loại T và M thuộc loại tuỳ ý |
dimensions |
Mảng int64 |
mảng các phương diện bản đồ |
Áp dụng một hàm vô hướng trên các mảng operands nhất định, tạo ra một mảng có cùng chiều, trong đó mỗi phần tử là kết quả của hàm đã liên kết được áp dụng cho các phần tử tương ứng trong mảng đầu vào.
Hàm đã liên kết là một tính toán tuỳ ý có giới hạn là hàm này có N đầu vào thuộc loại vô hướng T và một đầu ra duy nhất thuộc loại S. Dữ liệu đầu ra có cùng kích thước với toán hạng, ngoại trừ việc loại phần tử T được thay thế bằng S.
Ví dụ: Map(op1, op2, op3, computation, par1) ánh xạ elem_out <-
computation(elem1, elem2, elem3, par1) tại mỗi chỉ mục (đa chiều) trong mảng đầu vào để tạo mảng đầu ra.
OptimizationBarrier
Chặn mọi lượt truyền tối ưu hoá di chuyển các phép tính qua rào cản.
Đảm bảo rằng tất cả dữ liệu đầu vào đều được đánh giá trước mọi toán tử phụ thuộc vào đầu ra của rào cản.
Bàn phím
Xem thêm XlaBuilder::Pad.
Pad(operand, padding_value, padding_config)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
mảng thuộc loại T |
padding_value |
XlaOp |
đại lượng vô hướng thuộc loại T để lấp đầy khoảng đệm đã thêm |
padding_config |
PaddingConfig |
khoảng đệm ở cả hai cạnh (thấp, cao) và giữa các phần tử của mỗi kích thước |
Mở rộng mảng operand đã cho bằng cách thêm khoảng đệm xung quanh mảng cũng như giữa các phần tử của mảng bằng padding_value đã cho. padding_config chỉ định số lượng khoảng đệm cạnh và khoảng đệm bên trong cho mỗi kích thước.
PaddingConfig là một trường lặp lại của PaddingConfigDimension, chứa
ba trường cho mỗi phương diện: edge_padding_low, edge_padding_high và
interior_padding.
edge_padding_low và edge_padding_high chỉ định số lượng khoảng đệm được thêm ở cấp thấp (bên cạnh chỉ mục 0) và cao cấp (bên cạnh chỉ mục cao nhất) của từng chiều tương ứng. Khoảng đệm cạnh có thể là số âm – giá trị tuyệt đối của khoảng đệm âm cho biết số lượng phần tử cần xoá khỏi kích thước đã chỉ định.
interior_padding chỉ định khoảng đệm được thêm giữa hai phần tử bất kỳ trong mỗi nhóm; khoảng đệm này không được âm. Khoảng đệm bên trong xảy ra một cách logic trước khoảng đệm cạnh, vì vậy, trong trường hợp khoảng đệm cạnh âm, các phần tử sẽ bị xoá khỏi toán hạng có khoảng đệm bên trong.
Thao tác này không có tác dụng nếu tất cả các cặp khoảng đệm cạnh đều là (0, 0) và tất cả các giá trị khoảng đệm bên trong đều là 0. Hình dưới đây cho thấy các ví dụ về các giá trị edge_padding và interior_padding khác nhau cho một mảng hai chiều.
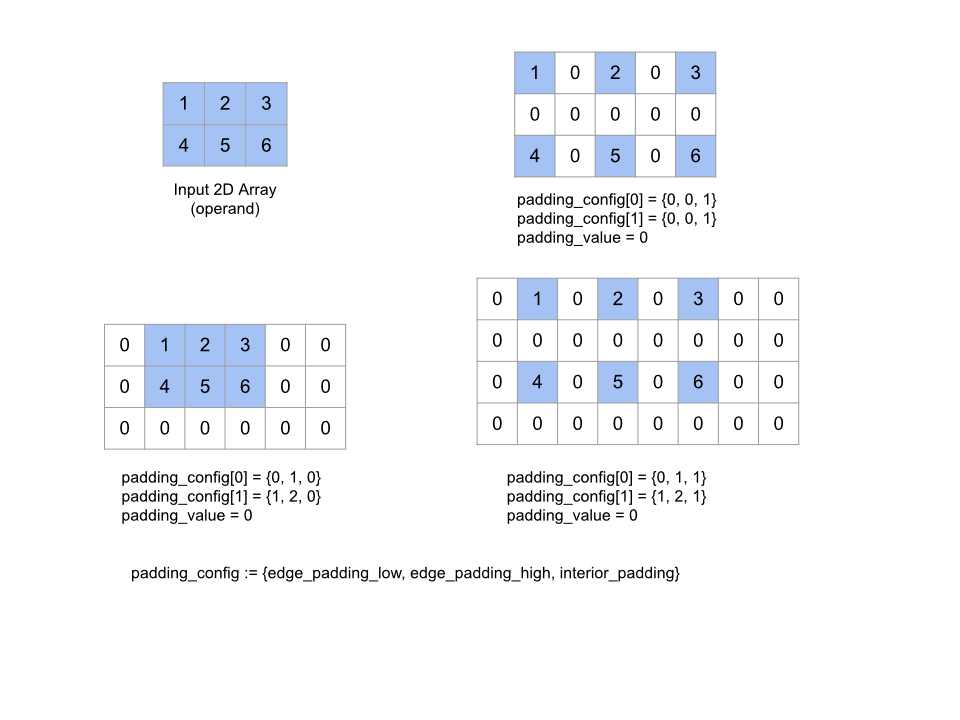
Recv
Xem thêm XlaBuilder::Recv.
Recv(shape, channel_handle)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
shape |
Shape |
hình dạng của dữ liệu cần nhận |
channel_handle |
ChannelHandle |
giá trị nhận dạng duy nhất cho mỗi cặp gửi/nhận |
Nhận dữ liệu của hình dạng đã cho từ một lệnh Send trong một phép tính khác có cùng một tay điều khiển kênh. Trả về một XlaOp cho dữ liệu đã nhận.
API ứng dụng của thao tác Recv đại diện cho giao tiếp đồng bộ.
Tuy nhiên, lệnh này được phân tách nội bộ thành 2 lệnh HLO (Recv và RecvDone) để cho phép chuyển dữ liệu không đồng bộ. Xem thêm HloInstruction::CreateRecv và HloInstruction::CreateRecvDone.
Recv(const Shape& shape, int64 channel_id)
Phân bổ tài nguyên cần thiết để nhận dữ liệu từ một lệnh Send có cùng channel_id. Trả về ngữ cảnh cho các tài nguyên được phân bổ, được sử dụng bởi lệnh RecvDone sau để chờ quá trình chuyển dữ liệu hoàn tất. Bối cảnh là một bộ dữ liệu gồm {receive buffer (shape), request identifier (U32)} và chỉ có thể được sử dụng bởi một lệnh RecvDone.
RecvDone(HloInstruction context)
Với ngữ cảnh được tạo bằng lệnh Recv, hãy chờ quá trình chuyển dữ liệu hoàn tất và trả về dữ liệu đã nhận.
Giảm bớt
Hãy xem thêm XlaBuilder::Reduce.
Áp dụng một hàm rút gọn cho một hoặc nhiều mảng song song.
Reduce(operands..., init_values..., computation, dimensions)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operands |
Chuỗi N XlaOp |
N mảng thuộc loại T_0, ..., T_{N-1}. |
init_values |
Trình tự N XlaOp |
N đại lượng vô hướng thuộc loại T_0, ..., T_{N-1}. |
computation |
XlaComputation |
phép tính kiểu T_0, ..., T_{N-1}, T_0, ..., T_{N-1} -> Collate(T_0, ..., T_{N-1}). |
dimensions |
Mảng int64 |
mảng không theo thứ tự của các phương diện cần giảm. |
Trong trường hợp:
- N phải lớn hơn hoặc bằng 1.
- Tính toán phải "gần như" có tính liên kết (xem bên dưới).
- Tất cả mảng đầu vào phải có cùng chiều.
- Tất cả giá trị ban đầu phải tạo thành một giá trị nhận dạng trong
computation. - Nếu
N = 1,Collate(T)làT. - Nếu
N > 1,Collate(T_0, ..., T_{N-1})là một bộ dữ liệu gồm các phần tửNthuộc loạiT.
Thao tác này sẽ giảm một hoặc nhiều chiều của mỗi mảng đầu vào thành các đại lượng vô hướng.
Thứ hạng của mỗi mảng được trả về là rank(operand) - len(dimensions). Đầu ra
của hoạt động là Collate(Q_0, ..., Q_N), trong đó Q_i là một mảng thuộc loại T_i,
kích thước được mô tả ở bên dưới.
Các phần phụ trợ khác nhau được phép liên kết lại phép tính rút gọn. Điều này có thể dẫn đến sự khác biệt về số học, vì một số hàm rút gọn như phép cộng không liên kết với số thực. Tuy nhiên, nếu phạm vi của dữ liệu bị giới hạn, thì phép cộng dấu phẩy động sẽ gần giống với phép liên kết cho hầu hết các trường hợp sử dụng thực tế.
Ví dụ
Khi rút gọn theo một chiều trong một mảng 1D có các giá trị [10, 11,
12, 13], với hàm rút gọn f (đây là computation), thì giá trị đó có thể được tính toán như sau
f(10, f(11, f(12, f(init_value, 13)))
nhưng cũng có nhiều khả năng khác, ví dụ:
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
Sau đây là một ví dụ mã giả gần đúng về cách triển khai khả năng rút gọn, sử dụng phép tính tổng làm phép tính rút gọn với giá trị ban đầu là 0.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the rank of the result
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
Sau đây là ví dụ về cách rút gọn một mảng 2D (matrice). Hình dạng có thứ hạng 2, kích thước 0 có kích thước 2 và kích thước 1 có kích thước 3:
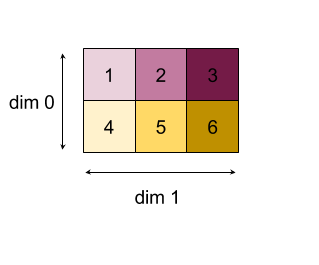
Kết quả của việc giảm kích thước 0 hoặc 1 bằng hàm "add" (thêm):
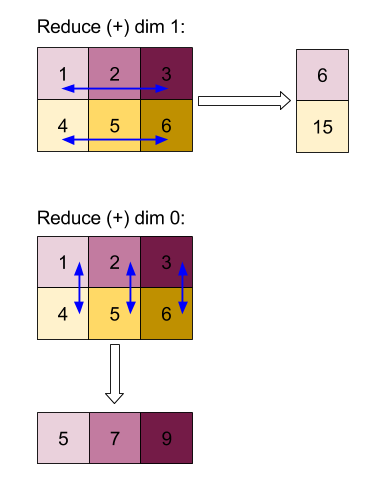
Xin lưu ý rằng cả hai kết quả rút gọn đều là mảng 1 chiều. Sơ đồ này hiển thị một cột và một hàng chỉ để thuận tiện cho việc xem.
Để biết ví dụ phức tạp hơn, sau đây là một mảng 3D. Hệ số này có thứ hạng là 3, kích thước 0 có kích thước 4, kích thước 1 có kích thước 2 và kích thước 2 có kích thước 3. Để đơn giản, các giá trị từ 1 đến 6 được sao chép trên phương diện 0.
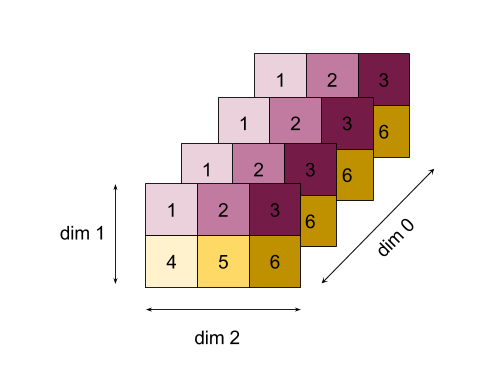
Tương tự như ví dụ 2D, chúng ta chỉ có thể giảm một kích thước. Ví dụ: nếu giảm phương diện 0, chúng ta sẽ nhận được một mảng thứ hạng 2 trong đó tất cả các giá trị trên phương diện 0 được thu gọn thành một đại lượng vô hướng:
| 4 8 12 |
| 16 20 24 |
Nếu giảm kích thước 2, chúng ta cũng sẽ nhận được một mảng thứ hạng 2, trong đó tất cả các giá trị trên kích thước 2 được gộp thành một đại lượng vô hướng:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
Xin lưu ý rằng thứ tự tương đối giữa các phương diện còn lại trong dữ liệu đầu vào được giữ nguyên trong dữ liệu đầu ra, nhưng một số phương diện có thể được chỉ định số mới (vì thứ hạng thay đổi).
Chúng tôi cũng có thể giảm nhiều phương diện. Việc thêm các chiều giảm 0 và 1 sẽ tạo ra mảng 1D [20, 28, 36].
Việc giảm mảng 3D trên tất cả các phương diện sẽ tạo ra đại lượng vô hướng 84.
Giảm biến
Khi N > 1, việc áp dụng hàm giảm sẽ phức tạp hơn một chút, vì hàm này được áp dụng đồng thời cho tất cả dữ liệu đầu vào. Các toán hạng được cung cấp cho phép tính theo thứ tự sau:
- Chạy giá trị giảm cho toán hạng đầu tiên
- ...
- Đang chạy giá trị giảm cho toán hạng thứ N
- Giá trị đầu vào cho toán hạng đầu tiên
- ...
- Giá trị đầu vào cho toán hạng thứ N
Ví dụ: hãy xem xét hàm rút gọn sau đây, có thể dùng để tính toán max và argmax của một mảng 1 chiều song song:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
Đối với các mảng Đầu vào 1-D V = Float[N], K = Int[N] và các giá trị khởi tạo I_V = Float, I_K = Int, kết quả f_(N-1) giảm trên phương diện đầu vào duy nhất sẽ tương đương với ứng dụng đệ quy sau đây:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
Việc áp dụng phép rút gọn này cho một mảng giá trị và một mảng chỉ mục tuần tự (tức là iota) sẽ cùng lặp lại trên các mảng và trả về một bộ chứa giá trị tối đa và chỉ mục khớp.
ReducePrecision
Xem thêm XlaBuilder::ReducePrecision.
Mô hình hoá hiệu ứng của việc chuyển đổi giá trị dấu phẩy động sang định dạng có độ chính xác thấp hơn (chẳng hạn như IEEE-FP16) và quay lại định dạng ban đầu. Bạn có thể chỉ định số bit mũ và số mũ thập phân trong định dạng có độ chính xác thấp một cách tuỳ ý, mặc dù tất cả kích thước bit có thể không được hỗ trợ trên tất cả các phương thức triển khai phần cứng.
ReducePrecision(operand, mantissa_bits, exponent_bits)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
mảng thuộc loại dấu phẩy động T. |
exponent_bits |
int32 |
số bit mũ ở định dạng có độ chính xác thấp hơn |
mantissa_bits |
int32 |
số bit của số mũ ở định dạng có độ chính xác thấp hơn |
Kết quả là một mảng thuộc loại T. Các giá trị đầu vào được làm tròn đến giá trị gần nhất có thể biểu thị bằng số bit dấu phẩy động nhất định (sử dụng ngữ nghĩa "được liên kết với số chẵn") và mọi giá trị vượt quá phạm vi do số bit mũ chỉ định sẽ được cố định thành số vô cực dương hoặc âm. Các giá trị NaN được giữ lại, mặc dù chúng có thể được chuyển đổi thành các giá trị NaN chuẩn.
Định dạng có độ chính xác thấp hơn phải có ít nhất một bit mũ (để phân biệt giá trị 0 với giá trị vô cực, vì cả hai đều có số mũ bằng 0) và phải có số bit số mũ không âm. Số bit mũ hoặc số thập phân có thể vượt quá giá trị tương ứng cho loại T; sau đó, phần tương ứng của lượt chuyển đổi chỉ là không hoạt động.
ReduceScatter
Hãy xem thêm XlaBuilder::ReduceScatter.
ReduceScatter là một toán tử tập hợp thực hiện hiệu quả một AllReduce, sau đó phân tán kết quả bằng cách chia kết quả đó thành các khối shard_count dọc theo scatter_dimension và bản sao i trong nhóm bản sao nhận được phân đoạn ith.
ReduceScatter(operand, computation, scatter_dim, shard_count,
replica_group_ids, channel_id)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng hoặc một bộ dữ liệu không trống gồm các mảng để giảm trên các bản sao. |
computation |
XlaComputation |
Tính toán rút gọn |
scatter_dimension |
int64 |
Phương diện để phân tán. |
shard_count |
int64 |
Số lượng khối cần tách scatter_dimension |
replica_groups |
vectơ của các vectơ của int64 |
Các nhóm thực hiện việc giảm |
channel_id |
không bắt buộc int64 |
Mã nhận dạng kênh không bắt buộc để giao tiếp giữa các mô-đun |
- Khi
operandlà một bộ dữ liệu gồm các mảng, thì hoạt động giảm-phát tán sẽ được thực hiện trên từng phần tử của bộ dữ liệu đó. replica_groupslà danh sách các nhóm bản sao sẽ thực hiện quá trình rút gọn (bạn có thể truy xuất mã nhận dạng bản sao cho bản sao hiện tại bằng cách sử dụngReplicaId). Thứ tự của các bản sao trong mỗi nhóm sẽ xác định thứ tự mà kết quả rút gọn sẽ được phân tán.replica_groupsphải trống (trong trường hợp này, tất cả bản sao đều thuộc về một nhóm) hoặc chứa cùng số phần tử giống với số bản sao. Khi có nhiều nhóm bản sao, thì tất cả các nhóm đó phải có cùng kích thước. Ví dụ:replica_groups = {0, 2}, {1, 3}thực hiện việc giảm giữa các bản sao0và2, cũng như1và3, sau đó phân tán kết quả.shard_countlà kích thước của mỗi nhóm bản sao. Chúng ta cần điều này trong trường hợpreplica_groupstrống. Nếureplica_groupskhông trống,shard_countphải bằng kích thước của mỗi nhóm bản sao.channel_idđược dùng để giao tiếp giữa các mô-đun: chỉ các thao tácreduce-scattercó cùngchannel_idmới có thể giao tiếp với nhau.
Hình dạng đầu ra là hình dạng đầu vào với scatter_dimension được làm nhỏ hơn shard_count lần. Ví dụ: nếu có 2 bản sao và toán hạng có giá trị [1.0, 2.25] và [3.0, 5.25] tương ứng trên 2 bản sao, thì giá trị đầu ra của op này, trong đó scatter_dim là 0 sẽ là [4.0] đối với bản sao đầu tiên và [7.5] đối với bản sao thứ hai.
ReduceWindow
Xem thêm XlaBuilder::ReduceWindow.
Áp dụng một hàm rút gọn cho tất cả phần tử trong mỗi cửa sổ của một trình tự gồm N mảng nhiều chiều, tạo ra một hoặc một bộ dữ liệu gồm N mảng nhiều chiều làm đầu ra. Mỗi mảng đầu ra có cùng số phần tử bằng số vị trí hợp lệ của cửa sổ. Lớp gộp có thể được biểu thị dưới dạng ReduceWindow. Tương tự như Reduce, computation được áp dụng luôn được truyền init_values ở bên trái.
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operands |
N XlaOps |
Một chuỗi gồm N mảng đa chiều thuộc loại T_0,..., T_{N-1}, mỗi mảng đại diện cho vùng cơ sở mà cửa sổ được đặt. |
init_values |
N XlaOps |
Giá trị N bắt đầu để rút gọn, một giá trị cho mỗi toán hạng N. Hãy xem phần Giảm để biết thông tin chi tiết. |
computation |
XlaComputation |
Hàm rút gọn thuộc loại T_0, ..., T_{N-1}, T_0, ..., T_{N-1} -> Collate(T_0, ..., T_{N-1}), để áp dụng cho các phần tử trong mỗi cửa sổ của tất cả các toán hạng đầu vào. |
window_dimensions |
ArraySlice<int64> |
mảng số nguyên cho các giá trị kích thước cửa sổ |
window_strides |
ArraySlice<int64> |
mảng số nguyên cho các giá trị bước cửa sổ |
base_dilations |
ArraySlice<int64> |
mảng số nguyên cho các giá trị giãn nở cơ số |
window_dilations |
ArraySlice<int64> |
mảng số nguyên cho các giá trị kéo giãn cửa sổ |
padding |
Padding |
loại khoảng đệm cho cửa sổ (Padding::kSame, giúp đệm để có cùng hình dạng đầu ra với đầu vào nếu bước là 1 hoặc Padding::kValid, không sử dụng khoảng đệm và "dừng" cửa sổ khi cửa sổ không còn vừa) |
Trong trường hợp:
- N phải lớn hơn hoặc bằng 1.
- Tất cả mảng đầu vào phải có cùng chiều.
- Nếu
N = 1,Collate(T)sẽ làT. - Nếu
N > 1,Collate(T_0, ..., T_{N-1})là một bộ dữ liệu gồm các phần tửNthuộc loại(T0,...T{N-1}).
Mã và hình bên dưới cho thấy ví dụ về cách sử dụng ReduceWindow. Dữ liệu đầu vào là một ma trận có kích thước [4x6] và cả window_dimensions và window_stride_dimensions đều là [2x3].
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
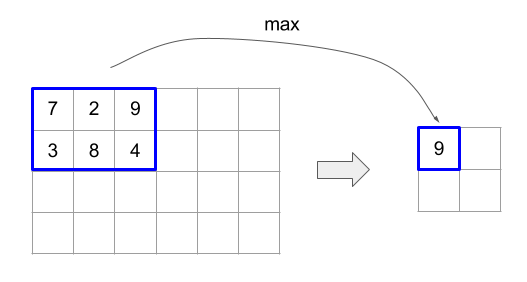
Bước 1 trong một phương diện chỉ định rằng vị trí của một cửa sổ trong phương diện đó cách cửa sổ liền kề 1 phần tử. Để chỉ định rằng không có cửa sổ nào chồng chéo lên nhau, window_stride_dimensions phải bằng window_dimensions. Hình dưới đây minh hoạ việc sử dụng hai giá trị bước khác nhau. Khoảng đệm được áp dụng cho từng kích thước của đầu vào và các phép tính sẽ giống như khi đầu vào có kích thước sau khoảng đệm.
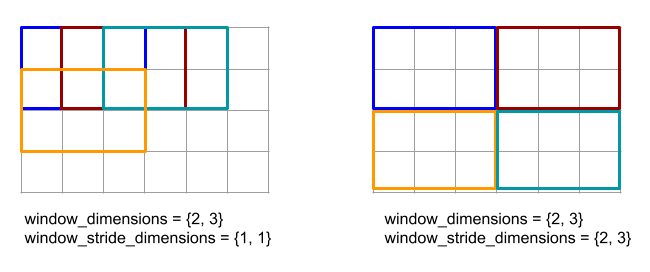
Đối với ví dụ về khoảng đệm không quan trọng, hãy cân nhắc tính toán giá trị tối thiểu của cửa sổ rút gọn (giá trị ban đầu là MAX_FLOAT) với kích thước 3 và bước 2 trên mảng đầu vào [10000, 1000, 100, 10, 1]. Padding kValid tính toán giá trị tối thiểu trên hai cửa sổ hợp lệ: [10000, 1000, 100] và [100, 10, 1], dẫn đến kết quả [100, 1]. Trước tiên, khoảng đệm kSame sẽ lót mảng sao cho hình dạng sau cửa sổ rút gọn sẽ giống với dữ liệu đầu vào để sải chân bằng cách thêm các phần tử ban đầu ở cả hai phía, nhận được [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]. Việc chạy reduce-window trên mảng được đệm sẽ hoạt động trên ba cửa sổ [MAX_VALUE, 10000, 1000], [1000, 100, 10], [10, 1, MAX_VALUE] và trả về [1000, 10, 1].
Thứ tự đánh giá của hàm rút gọn là tuỳ ý và có thể không xác định. Do đó, hàm rút gọn không được quá nhạy cảm với việc liên kết lại. Hãy xem nội dung thảo luận về tính liên kết trong ngữ cảnh của Reduce để biết thêm chi tiết.
ReplicaId
Hãy xem thêm XlaBuilder::ReplicaId.
Trả về mã nhận dạng duy nhất (vô hướng U32) của bản sao.
ReplicaId()
Mã nhận dạng duy nhất của mỗi bản sao là một số nguyên chưa ký trong khoảng [0, N), trong đó N là số lượng bản sao. Vì tất cả các bản sao đều đang chạy cùng một chương trình, nên lệnh gọi ReplicaId() trong chương trình sẽ trả về một giá trị khác nhau trên mỗi bản sao.
Định hình lại
Hãy xem thêm
XlaBuilder::Reshape
và toán tử Collapse.
Định hình lại các phương diện của một mảng thành một cấu hình mới.
Reshape(operand, new_sizes)
Reshape(operand, dimensions, new_sizes)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
mảng thuộc loại T |
dimensions |
Vectơ int64 |
thứ tự thu gọn các phương diện |
new_sizes |
Vectơ int64 |
vectơ kích thước của các phương diện mới |
Về mặt khái niệm, trước tiên, hàm reshape làm phẳng một mảng thành một vectơ một chiều của các giá trị dữ liệu, sau đó tinh chỉnh vectơ này thành một hình dạng mới. Đối số đầu vào là một mảng tuỳ ý thuộc loại T, vectơ hằng số thời gian biên dịch của các chỉ số kích thước và vectơ hằng số trong thời gian biên dịch có kích thước kích thước cho kết quả.
Các giá trị trong vectơ dimension (nếu có) phải là một hoán vị của tất cả các kích thước của T; giá trị mặc định nếu không có là {0, ..., rank - 1}. Thứ tự của các phương diện trong dimensions là từ phương diện thay đổi chậm nhất (chính nhất) đến phương diện thay đổi nhanh nhất (phụ nhất) trong lồng lặp, giúp thu gọn mảng đầu vào thành một phương diện duy nhất. Vectơ new_sizes xác định kích thước của mảng đầu ra. Giá trị tại chỉ mục 0 trong new_sizes là kích thước của kích thước 0, giá trị tại chỉ mục 1 là kích thước của kích thước 1, v.v. Tích của các phương diện new_size phải bằng tích của kích thước phương diện của toán hạng. Khi tinh chỉnh mảng đã thu gọn thành mảng đa chiều do new_sizes xác định, các kích thước trong new_sizes được sắp xếp theo thứ tự từ biến thể chậm nhất (hầu hết chính) đến thay đổi nhanh nhất (hầu hết là phụ).
Ví dụ: giả sử v là một mảng gồm 24 phần tử:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
In-order collapse:
let v012_24 = Reshape(v, {0,1,2}, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {0,1,2}, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
Out-of-order collapse:
let v021_24 = Reshape(v, {1,2,0}, {24});
then v012_24 == f32[24] {10, 20, 30, 40, 11, 21, 31, 41, 12, 22, 32, 42,
15, 25, 35, 45, 16, 26, 36, 46, 17, 27, 37, 47};
let v021_83 = Reshape(v, {1,2,0}, {8,3});
then v021_83 == f32[8x3] { {10, 20, 30}, {40, 11, 21},
{31, 41, 12}, {22, 32, 42},
{15, 25, 35}, {45, 16, 26},
{36, 46, 17}, {27, 37, 47} };
let v021_262 = Reshape(v, {1,2,0}, {2,6,2});
then v021_262 == f32[2x6x2] { { {10, 20}, {30, 40},
{11, 21}, {31, 41},
{12, 22}, {32, 42} },
{ {15, 25}, {35, 45},
{16, 26}, {36, 46},
{17, 27}, {37, 47} } };
Trong trường hợp đặc biệt, reshape có thể chuyển đổi một mảng có một phần tử thành một đại lượng vô hướng và ngược lại. Ví dụ:
Reshape(f32[1x1] { {5} }, {0,1}, {}) == 5;
Reshape(5, {}, {1,1}) == f32[1x1] { {5} };
Doanh thu (đảo ngược)
Xem thêm XlaBuilder::Rev.
Rev(operand, dimensions)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
mảng thuộc loại T |
dimensions |
ArraySlice<int64> |
các tham số cần đảo ngược |
Đảo ngược thứ tự các phần tử trong mảng operand dọc theo dimensions đã chỉ định, tạo ra một mảng đầu ra có cùng hình dạng. Mỗi phần tử của mảng toán hạng tại một chỉ mục đa chiều được lưu trữ vào mảng đầu ra tại một chỉ mục đã chuyển đổi. Chỉ mục đa chiều được biến đổi bằng cách đảo ngược chỉ mục trong mỗi chiều cần đảo ngược (nghĩa là nếu thứ nguyên có kích thước N là một trong các chiều đảo ngược, thì chỉ mục i của chỉ số đó được chuyển đổi thành N - 1 - i).
Một cách sử dụng toán tử Rev là đảo ngược mảng trọng số tích chập dọc theo hai kích thước cửa sổ trong quá trình tính toán độ dốc trong mạng nơron.
RngNormal
Xem thêm XlaBuilder::RngNormal.
Tạo một đầu ra có hình dạng nhất định bằng các số ngẫu nhiên được tạo theo phân phối chuẩn . Các tham số và , cũng như hình dạng đầu ra phải có loại phần tử dấu phẩy động. Ngoài ra, các tham số phải có giá trị vô hướng.
RngNormal(mu, sigma, shape)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
mu |
XlaOp |
Số thực thuộc loại T chỉ định giá trị trung bình của các số được tạo |
sigma |
XlaOp |
Vô hướng loại T xác định độ lệch chuẩn của được tạo |
shape |
Shape |
Hình dạng đầu ra thuộc loại T |
RngUniform
Xem thêm XlaBuilder::RngUniform.
Tạo đầu ra của một hình dạng cho trước với các số ngẫu nhiên được tạo theo phân phối đồng nhất trong khoảng . Thông số và loại phần tử đầu ra phải là loại boolean, loại số nguyên hoặc loại dấu phẩy động và các loại này phải nhất quán. Phần phụ trợ CPU và GPU hiện chỉ hỗ trợ F64, F32, F16, BF16, S64, U64, S32 và U32. Hơn nữa, các tham số cần có giá trị vô hướng. Nếu kết quả là do quá trình triển khai xác định.
RngUniform(a, b, shape)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
a |
XlaOp |
Số thực thuộc loại T chỉ định giới hạn dưới của khoảng |
b |
XlaOp |
Số thực của loại T chỉ định giới hạn trên của khoảng thời gian |
shape |
Shape |
Hình dạng đầu ra thuộc loại T |
RngBitGenerator
Tạo một đầu ra có hình dạng nhất định được lấp đầy bằng các bit ngẫu nhiên đồng nhất bằng cách sử dụng thuật toán được chỉ định (hoặc mặc định của phần phụ trợ) và trả về trạng thái đã cập nhật (có hình dạng giống với trạng thái ban đầu) và dữ liệu ngẫu nhiên đã tạo.
Trạng thái ban đầu là trạng thái ban đầu của quá trình tạo số ngẫu nhiên hiện tại. Nó cũng như hình dạng được yêu cầu và các giá trị hợp lệ phụ thuộc vào thuật toán được sử dụng.
Đầu ra được đảm bảo là một hàm xác định trước của trạng thái ban đầu, nhưng không được đảm bảo là xác định trước giữa các phần phụ trợ và các phiên bản trình biên dịch khác nhau.
RngBitGenerator(algorithm, key, shape)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
algorithm |
RandomAlgorithm |
Thuật toán PRNG sẽ được sử dụng. |
initial_state |
XlaOp |
Trạng thái ban đầu cho thuật toán PRNG. |
shape |
Shape |
Hình dạng đầu ra cho dữ liệu được tạo. |
Các giá trị có thể sử dụng cho algorithm:
rng_default: Thuật toán dành riêng cho phần phụ trợ với các yêu cầu về hình dạng dành riêng cho phần phụ trợ.rng_three_fry: Thuật toán PRNG dựa trên bộ đếm ThreeFry. Hình dạnginitial_statelàu64[2]với các giá trị tuỳ ý. Salmon và cộng sự SC 2011. Số ngẫu nhiên song song: dễ dàng như việc đếm 1, 2, 3.rng_philox: Thuật toán Philox để tạo số ngẫu nhiên song song. Hình dạnginitial_statelàu64[3]với các giá trị tuỳ ý. Salmon et al. SC 2011. Số ngẫu nhiên song song: dễ dàng như việc đếm 1, 2, 3.
Tán xạ
Toán tử phân tán XLA tạo ra một chuỗi kết quả là các giá trị của mảng đầu vào operands, với một số lát cắt (tại các chỉ mục do scatter_indices chỉ định) được cập nhật bằng chuỗi giá trị trong updates bằng cách sử dụng update_computation.
Hãy xem thêm XlaBuilder::Scatter.
scatter(operands..., scatter_indices, updates..., update_computation,
index_vector_dim, update_window_dims, inserted_window_dims,
scatter_dims_to_operand_dims)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operands |
Chuỗi N XlaOp |
N mảng thuộc loại T_0, ..., T_N được phân tán vào. |
scatter_indices |
XlaOp |
Mảng chứa các chỉ mục bắt đầu của các lát cắt phải được phân tán đến. |
updates |
Chuỗi N XlaOp |
N mảng thuộc loại T_0, ..., T_N. updates[i] chứa các giá trị phải được dùng để tán xạ operands[i]. |
update_computation |
XlaComputation |
Phép tính được dùng để kết hợp các giá trị hiện có trong mảng đầu vào và nội dung cập nhật trong quá trình phân tán. Kết quả tính toán này phải thuộc loại T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N). |
index_vector_dim |
int64 |
Phương diện trong scatter_indices chứa các chỉ mục bắt đầu. |
update_window_dims |
ArraySlice<int64> |
Tập hợp kích thước ở hình dạng updates là kích thước cửa sổ. |
inserted_window_dims |
ArraySlice<int64> |
Tập hợp kích thước cửa sổ phải được chèn vào hình dạng updates. |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
Bản đồ kích thước từ chỉ mục tán xạ đến không gian chỉ mục toán hạng. Mảng này được diễn giải là ánh xạ i đến scatter_dims_to_operand_dims[i] . Số liệu phải là một với một và tổng cộng. |
indices_are_sorted |
bool |
Liệu các chỉ mục có được đảm bảo là được sắp xếp theo phương thức gọi hay không. |
unique_indices |
bool |
Liệu chỉ số có được đảm bảo là duy nhất bởi phương thức gọi hay không. |
Trong trường hợp:
- N phải lớn hơn hoặc bằng 1.
operands[0], ...,operands[N-1] đều phải có cùng phương diện.updates[0], ...,updates[N-1] phải có cùng kích thước.- Nếu
N = 1,Collate(T)sẽ làT. - Nếu
N > 1,Collate(T_0, ..., T_N)là một bộ dữ liệu gồm các phần tửNthuộc loạiT.
Nếu index_vector_dim bằng scatter_indices.rank, chúng tôi ngầm xem scatter_indices là có phương diện 1 kéo dài.
Chúng tôi xác định update_scatter_dims thuộc loại ArraySlice<int64> làm tập hợp kích thước trong hình dạng updates không có trong update_window_dims, theo thứ tự tăng dần.
Các đối số của hàm phân tán phải tuân theo các quy tắc ràng buộc sau:
Mỗi mảng
updatesphải có thứ hạngupdate_window_dims.size + scatter_indices.rank - 1.Giới hạn của phương diện
itrong mỗi mảngupdatesphải tuân theo các quy tắc sau:- Nếu
ixuất hiện trongupdate_window_dims(tức là bằngupdate_window_dims[k] đối với một sốk), thì giới hạn của kích thướcitrongupdateskhông được vượt quá giới hạn tương ứng củaoperandsau khi tính đếninserted_window_dims(tức làadjusted_window_bounds[k], trong đóadjusted_window_boundschứa giới hạn củaoperandvà giới hạn tại các chỉ mụcinserted_window_dimsđã bị xoá). - Nếu
icó trongupdate_scatter_dims(tức là bằngupdate_scatter_dims[k] đối với một sốk), thì giới hạn của kích thướcitrongupdatesphải bằng giới hạn tương ứng củascatter_indices, bỏ quaindex_vector_dim(tức làscatter_indices.shape.dims[k], nếuk<index_vector_dimvàscatter_indices.shape.dims[k+1] nếu không).
- Nếu
update_window_dimsphải theo thứ tự tăng dần, không có số kích thước lặp lại và nằm trong phạm vi[0, updates.rank).inserted_window_dimsphải theo thứ tự tăng dần, không có số phương diện lặp lại và nằm trong phạm vi[0, operand.rank).operand.rankphải bằng tổng củaupdate_window_dims.sizevàinserted_window_dims.size.scatter_dims_to_operand_dims.sizephải bằngscatter_indices.shape.dims[index_vector_dim] và các giá trị của nó phải nằm trong dải[0, operand.rank).
Đối với một chỉ mục U nhất định trong mỗi mảng updates, chỉ mục I tương ứng trong mảng operands tương ứng mà bạn phải áp dụng nội dung cập nhật này được tính toán như sau:
- Đặt
G= {U[k] choktrongupdate_scatter_dims}. Sử dụngGđể tra cứu vectơ chỉ mụcStrong mảngscatter_indicessao choS[i] =scatter_indices[Kết hợp(G,i)] trong đó kết hợp(A, b) sẽ chèn b tại các vị tríindex_vector_dimvào A. - Tạo chỉ mục
Sinvàooperandbằng cách sử dụngSbằng cách phân tánSbằng bản đồscatter_dims_to_operand_dims. Chính thức hơn:Sin[scatter_dims_to_operand_dims[k]] =S[k] nếuk<scatter_dims_to_operand_dims.size.Sin[_] =0.
- Tạo một chỉ mục
Winvào mỗi mảngoperandsbằng cách phân tán các chỉ mục tạiupdate_window_dimstrongUtheoinserted_window_dims. Chính thức hơn:Win[window_dims_to_operand_dims(k)] =U[k] nếuknằm trongupdate_window_dims, trong đówindow_dims_to_operand_dimslà hàm tăng dần với miền [0,update_window_dims.size) và dải ô [0,operand.rank) \inserted_window_dims. (Ví dụ: nếuupdate_window_dims.sizelà4,operand.ranklà6vàinserted_window_dimslà {0,2}, thìwindow_dims_to_operand_dimslà {0→1,1→3,2→4,3→5}).Win[_] =0nếu không.
IlàWin+Sin, trong đó + là phép bổ sung phần tử.
Tóm lại, bạn có thể xác định toán tử tán xạ như sau.
- Khởi chạy
outputbằngoperands, tức là cho tất cả các chỉ mụcJ, cho tất cả các chỉ mụcOtrong mảngoperands[J]:output[J][O] =operands[J][O] - Đối với mọi chỉ mục
Utrong mảngupdates[J] và chỉ mục tương ứngOtrong mảngoperand[J], nếuOlà chỉ mục hợp lệ chooutput:(output[0][O], ...,output[N-1][O])=update_computation(output[0][O], ...,output[N-1][O],updates[0][U], ...,updates[N-1][U])
Thứ tự áp dụng các bản cập nhật là không xác định. Vì vậy, khi nhiều chỉ mục trong updates tham chiếu đến cùng một chỉ mục trong operands, thì giá trị tương ứng trong output sẽ không xác định.
Lưu ý rằng tham số đầu tiên được truyền vào update_computation sẽ luôn là giá trị hiện tại của mảng output và tham số thứ hai sẽ luôn là giá trị của mảng updates. Điều này đặc biệt quan trọng đối với các trường hợp update_computation không giao hoán.
Nếu bạn đặt indices_are_sorted thành true, thì XLA có thể giả định rằng scatter_indices được người dùng sắp xếp (theo thứ tự tăng dần, sau khi phân tán các giá trị theo scatter_dims_to_operand_dims). Nếu không, ngữ nghĩa sẽ được xác định bằng cách triển khai.
Nếu unique_indices được đặt thành true, thì XLA có thể giả định rằng tất cả các phần tử được phân tán đều là duy nhất. Vì vậy, XLA có thể sử dụng các thao tác không nguyên tử. Nếu bạn đặt unique_indices thành true và các chỉ mục được phân tán không phải là duy nhất, thì ngữ nghĩa sẽ được xác định bằng cách triển khai.
Không chính thức, toán tử tán xạ có thể được xem là ngược của toán tử thu thập, tức là toán tử tán xạ cập nhật các phần tử trong dữ liệu đầu vào được trích xuất bằng toán tử thu thập tương ứng.
Để xem ví dụ và nội dung mô tả chi tiết, không chính thức, hãy tham khảo phần "Nội dung mô tả không chính thức" trong Gather.
Chọn
Xem thêm XlaBuilder::Select.
Tạo một mảng đầu ra từ các phần tử của hai mảng đầu vào, dựa trên giá trị của một mảng thuộc tính.
Select(pred, on_true, on_false)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
pred |
XlaOp |
mảng thuộc loại PRED |
on_true |
XlaOp |
mảng thuộc loại T |
on_false |
XlaOp |
mảng thuộc loại T |
Mảng on_true và on_false phải có cùng hình dạng. Đây cũng là hình dạng của mảng đầu ra. Mảng pred phải có cùng thứ nguyên với on_true và on_false, với loại phần tử PRED.
Đối với mỗi phần tử P của pred, phần tử tương ứng của mảng đầu ra được lấy từ on_true nếu giá trị của P là true và từ on_false nếu giá trị của P là false. Là một dạng truyền tin bị hạn chế, pred có thể là một đại lượng vô hướng thuộc loại PRED. Trong trường hợp này, mảng đầu ra được lấy hoàn toàn từ on_true nếu pred là true và từ on_false nếu pred là false.
Ví dụ với pred không vô hướng:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
Ví dụ với vectơ pred:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
Hỗ trợ lựa chọn giữa các bộ dữ liệu. Đối với mục đích này, các bộ dữ liệu được coi là loại vô hướng. Nếu on_true và on_false là các bộ dữ liệu (phải có cùng hình dạng!), thì pred phải là một đại lượng vô hướng thuộc kiểu PRED.
SelectAndScatter
Xem thêm XlaBuilder::SelectAndScatter.
Bạn có thể coi toán tử này là một toán tử tổng hợp, trước tiên sẽ tính toán ReduceWindow trên mảng operand để chọn một phần tử từ mỗi cửa sổ, sau đó phân tán mảng source đến các chỉ mục của các phần tử đã chọn để tạo một mảng đầu ra có cùng hình dạng với mảng toán hạng. Hàm select nhị phân được dùng để chọn một phần tử từ mỗi cửa sổ bằng cách áp dụng hàm đó trên mỗi cửa sổ và được gọi bằng thuộc tính là vectơ chỉ mục của tham số đầu tiên nhỏ hơn vectơ chỉ mục của tham số thứ hai theo thứ tự bảng chữ cái. Hàm select trả về true nếu tham số đầu tiên được chọn và trả về false nếu tham số thứ hai được chọn, đồng thời hàm phải giữ tính chất bắc cầu (tức là nếu select(a, b) và select(b, c) là true, thì select(a, c) cũng là true) để phần tử được chọn không phụ thuộc vào thứ tự của các phần tử được di chuyển qua một cửa sổ nhất định.
Hàm scatter được áp dụng tại mỗi chỉ mục đã chọn trong mảng đầu ra. Hàm này nhận 2 tham số vô hướng:
- Giá trị hiện tại tại chỉ mục đã chọn trong mảng đầu ra
- Giá trị tán xạ từ
sourceáp dụng cho chỉ mục đã chọn
Phương thức này kết hợp 2 tham số và trả về một giá trị vô hướng dùng để cập nhật giá trị ở chỉ mục đã chọn trong mảng đầu ra. Ban đầu, tất cả chỉ mục của mảng đầu ra đều được đặt thành init_value.
Mảng đầu ra có cùng hình dạng với mảng operand và mảng source phải có cùng hình dạng như kết quả của việc áp dụng toán tử ReduceWindow trên mảng operand. Bạn có thể dùng SelectAndScatter để truyền ngược các giá trị độ dốc cho một lớp gộp trong mạng nơron.
SelectAndScatter(operand, select, window_dimensions, window_strides,
padding, source, init_value, scatter)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
mảng loại T mà qua đó các cửa sổ trượt qua |
select |
XlaComputation |
tính toán nhị phân thuộc loại T, T -> PRED, để áp dụng cho tất cả các phần tử trong mỗi cửa sổ; trả về true nếu tham số đầu tiên được chọn và trả về false nếu tham số thứ hai được chọn |
window_dimensions |
ArraySlice<int64> |
mảng số nguyên cho các giá trị phương diện cửa sổ |
window_strides |
ArraySlice<int64> |
mảng số nguyên cho các giá trị bước cửa sổ |
padding |
Padding |
loại khoảng đệm cho cửa sổ (Padding::kSame hoặc Padding::kValid) |
source |
XlaOp |
mảng thuộc loại T với các giá trị cần phân tán |
init_value |
XlaOp |
giá trị vô hướng thuộc loại T cho giá trị ban đầu của mảng đầu ra |
scatter |
XlaComputation |
tính toán nhị phân của loại T, T -> T, để áp dụng từng phần tử nguồn phân tán với phần tử đích của nó |
Hình dưới đây cho thấy ví dụ về cách sử dụng SelectAndScatter, với hàm select tính toán giá trị tối đa trong số các tham số của hàm đó. Lưu ý rằng khi các cửa sổ chồng lên nhau, như trong hình (2) bên dưới, một chỉ mục của mảng operand có thể được nhiều cửa sổ chọn nhiều lần. Trong hình, phần tử có giá trị 9 được cả hai cửa sổ trên cùng (xanh dương và đỏ) chọn và hàm scatter cộng nhị phân tạo ra phần tử đầu ra có giá trị 8 (2 + 6).
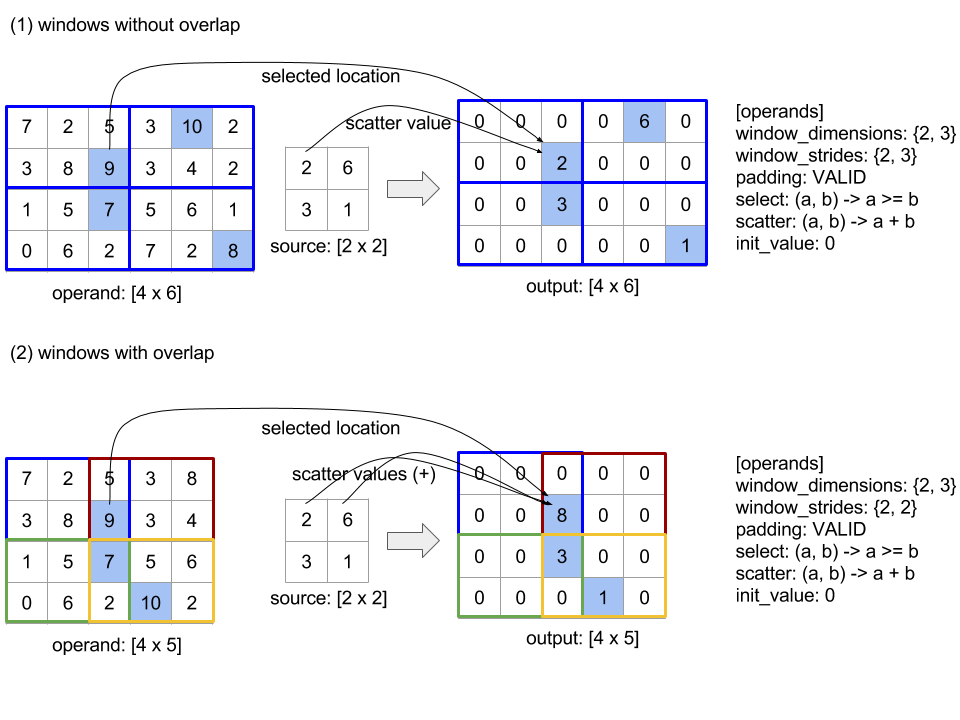
Thứ tự đánh giá của hàm scatter là tuỳ ý và có thể không xác định. Do đó, hàm scatter không được quá nhạy cảm với việc liên kết lại. Hãy xem phần thảo luận về tính liên kết trong ngữ cảnh của Reduce để biết thêm chi tiết.
Gửi
Hãy xem thêm XlaBuilder::Send.
Send(operand, channel_handle)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
dữ liệu cần gửi (mảng thuộc loại T) |
channel_handle |
ChannelHandle |
giá trị nhận dạng duy nhất cho mỗi cặp gửi/nhận |
Gửi dữ liệu toán hạng đã cho đến một lệnh Recv trong một phép tính khác có cùng một tay điều khiển kênh. Không trả về dữ liệu nào.
Tương tự như toán tử Recv, API ứng dụng của toán tử Send đại diện cho giao tiếp đồng bộ và được phân ly nội bộ thành 2 lệnh HLO (Send và SendDone) để cho phép chuyển dữ liệu không đồng bộ. Xem thêm HloInstruction::CreateSend và HloInstruction::CreateSendDone.
Send(HloInstruction operand, int64 channel_id)
Bắt đầu quá trình chuyển không đồng bộ của toán hạng đến các tài nguyên do lệnh Recv phân bổ có cùng mã nhận dạng kênh. Trả về một ngữ cảnh được lệnh SendDone sau đây sử dụng để chờ quá trình chuyển dữ liệu hoàn tất. Ngữ cảnh là một bộ dữ liệu của {operand (hình dạng), giá trị nhận dạng yêu cầu (U32)} và chỉ có thể sử dụng bằng lệnh SendDone.
SendDone(HloInstruction context)
Với bối cảnh được tạo bằng lệnh Send, hãy chờ quá trình chuyển dữ liệu hoàn tất. Lệnh này không trả về bất kỳ dữ liệu nào.
Lên lịch cho hướng dẫn trên kênh
Thứ tự thực thi của 4 lệnh cho mỗi kênh (Recv, RecvDone, Send, SendDone) như bên dưới.
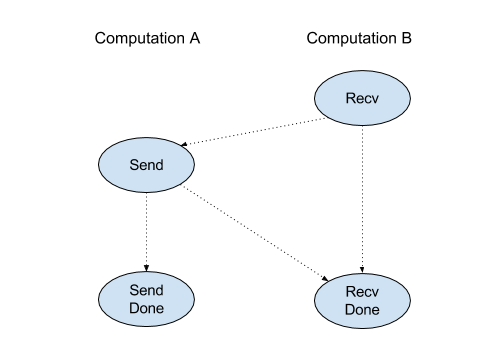
Recvxảy ra trướcSendSenddiễn ra trướcRecvDoneRecvxảy ra trướcRecvDoneSendxảy ra trướcSendDone
Khi trình biên dịch phụ trợ tạo lịch biểu tuyến tính cho mỗi phép tính giao tiếp qua hướng dẫn kênh, không được có chu kỳ trên các phép tính. Ví dụ: các lịch biểu dưới đây dẫn đến tắc nghẽn.
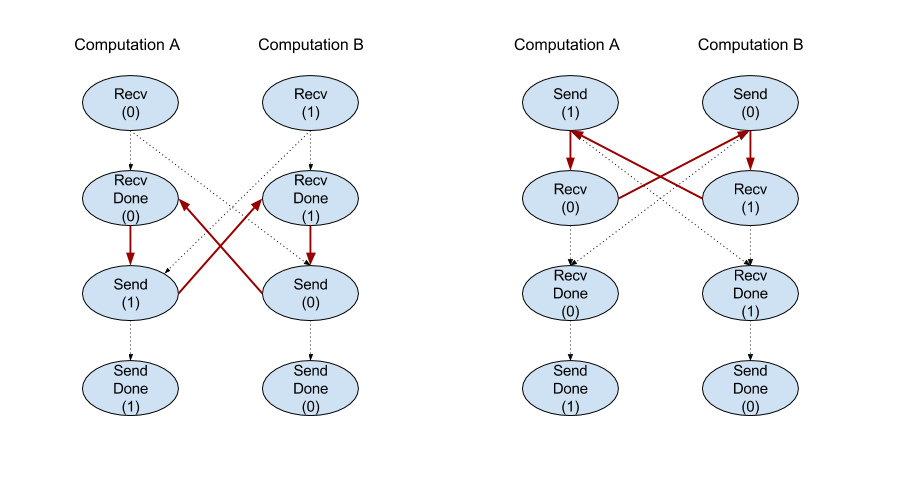
Slice (lát cắt)
Xem thêm XlaBuilder::Slice.
Thao tác cắt sẽ trích xuất một mảng con từ mảng đầu vào. Mảng con có cùng thứ hạng với dữ liệu đầu vào và chứa các giá trị bên trong một hộp giới hạn trong mảng đầu vào, nơi các kích thước và chỉ mục của hộp giới hạn được đưa ra làm đối số cho thao tác cắt.
Slice(operand, start_indices, limit_indices, strides)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Mảng N chiều thuộc loại T |
start_indices |
ArraySlice<int64> |
Danh sách N số nguyên chứa chỉ mục bắt đầu của lát cắt cho mỗi chiều. Giá trị phải lớn hơn hoặc bằng 0. |
limit_indices |
ArraySlice<int64> |
Danh sách các số nguyên N chứa các chỉ mục kết thúc (không bao gồm) cho lát cắt cho mỗi phương diện. Mỗi giá trị phải lớn hơn hoặc bằng giá trị start_indices tương ứng của phương diện và nhỏ hơn hoặc bằng kích thước của phương diện. |
strides |
ArraySlice<int64> |
Danh sách các số nguyên N quyết định bước đầu vào của lát cắt. Lát cắt này chọn mọi phần tử strides[d] trong phương diện d. |
Ví dụ về 1 chiều:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4}) produces:
{2.0, 3.0}
Ví dụ về 2 chiều:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3}) produces:
{ { 7.0, 8.0},
{10.0, 11.0} }
Sắp xếp
Xem thêm XlaBuilder::Sort.
Sort(operands, comparator, dimension, is_stable)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operands |
ArraySlice<XlaOp> |
Các toán hạng cần sắp xếp. |
comparator |
XlaComputation |
Phép tính so sánh sẽ sử dụng. |
dimension |
int64 |
Phương diện để sắp xếp. |
is_stable |
bool |
Liệu có nên sử dụng tính năng sắp xếp ổn định hay không. |
Nếu chỉ cung cấp một toán hạng:
Nếu toán hạng là một tensor bậc 1 (mảng), thì kết quả sẽ là một mảng đã sắp xếp. Nếu bạn muốn sắp xếp mảng theo thứ tự tăng dần, trình so sánh sẽ thực hiện phép so sánh nhỏ hơn. Về mặt chính thức, sau khi mảng được sắp xếp, mảng này sẽ giữ nguyên tất cả các vị trí chỉ mục
i, jvớii < jlàcomparator(value[i], value[j]) = comparator(value[j], value[i]) = falsehoặccomparator(value[i], value[j]) = true.Nếu toán hạng có thứ hạng cao hơn, thì toán hạng đó sẽ được sắp xếp theo phương diện được cung cấp. Ví dụ: đối với một tensor cấp 2 (matrice), giá trị phương diện là
0sẽ sắp xếp độc lập từng cột và giá trị phương diện là1sẽ sắp xếp độc lập từng hàng. Nếu không cung cấp số phương diện, thì phương diện cuối cùng sẽ được chọn theo mặc định. Đối với thứ tự được sắp xếp, thứ tự sắp xếp tương tự sẽ áp dụng như trong trường hợp thứ hạng 1.
Nếu cung cấp toán hạng n > 1:
Tất cả toán hạng
nphải là tensor có cùng kích thước. Các loại phần tử của tensor có thể khác nhau.Tất cả toán hạng được sắp xếp cùng nhau, chứ không phải riêng lẻ. Về mặt khái niệm, các toán hạng được coi là một bộ dữ liệu. Khi kiểm tra xem có cần hoán đổi các phần tử của mỗi toán hạng ở vị trí chỉ mục
ivàjhay không, trình so sánh được gọi bằng các tham số vô hướng2 * n, trong đó tham số2 * ktương ứng với giá trị ở vị tríicủa toán hạngk-thvà tham số2 * k + 1tương ứng với giá trị ở vị tríjcủa toán hạngk-th. Do đó, thông thường, trình so sánh sẽ so sánh các tham số2 * kvà2 * k + 1với nhau và có thể sử dụng các cặp tham số khác làm giá trị phân định khi có nhiều giá trị bằng nhau.Kết quả là một bộ dữ liệu gồm các toán hạng theo thứ tự đã sắp xếp (dọc theo phương diện đã cung cấp, như trên). Toán hạng
i-thcủa bộ dữ liệu tương ứng với toán hạngi-thcủa Sort.
Ví dụ: nếu có 3 toán hạng operand0 = [3, 1], operand1 = [42, 50], operand2 = [-3.0, 1.1] và trình so sánh chỉ so sánh các giá trị của operand0 với giá trị nhỏ hơn, thì kết quả của cách sắp xếp sẽ là bộ dữ liệu ([1, 3], [50, 42], [1.1, -3.0]).
Nếu is_stable được đặt thành đúng, thì việc sắp xếp được đảm bảo là ổn định, tức là nếu có các phần tử được trình so sánh coi là bằng nhau, thì thứ tự tương đối của các giá trị bằng nhau sẽ được giữ nguyên. Hai phần tử e1 và e2 bằng nhau nếu và chỉ khi comparator(e1, e2) = comparator(e2, e1) = false. Theo mặc định, is_stable được đặt thành false.
Chuyển đổi
Xem thêm toán tử tf.reshape.
Transpose(operand)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
operand |
XlaOp |
Toán hạng cần hoán vị. |
permutation |
ArraySlice<int64> |
Cách bật tiếng các phương diện. |
Hoán vị các chiều toán hạng bằng phép hoán vị cho trước, vì vậy ∀ i . 0 ≤ i < rank ⇒ input_dimensions[permutation[i]] = output_dimensions[i].
Hàm này giống với Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)).
TriangularSolve
Xem thêm XlaBuilder::TriangularSolve.
Giải hệ phương trình tuyến tính có ma trận hệ số tam giác dưới hoặc trên bằng phép thay thế trực tiếp hoặc ngược. Truyền theo các kích thước dẫn đầu, quy trình này giải một trong các hệ thống ma trận op(a) * x =
b hoặc x * op(a) = b cho biến x, với a và b, trong đó op(a) là op(a) = a, op(a) = Transpose(a) hoặc op(a) = Conj(Transpose(a)).
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
a |
XlaOp |
một mảng > 2 thuộc loại phức hoặc dấu phẩy động có hình dạng [..., M, M]. |
b |
XlaOp |
một mảng > 2 cùng loại có hình dạng [..., M, K] nếu left_side là đúng, nếu không thì là [..., K, M]. |
left_side |
bool |
cho biết cần giải hệ thống có dạng op(a) * x = b (true) hay x * op(a) = b (false). |
lower |
bool |
liệu có nên sử dụng tam giác trên hay dưới của a. |
unit_diagonal |
bool |
nếu true, các phần tử đường chéo của a được giả định là 1 và không được truy cập. |
transpose_a |
Transpose |
liệu có sử dụng a nguyên trạng, chuyển đổi ma trận này hay lấy ma trận chuyển đổi phức hợp của ma trận này. |
Dữ liệu đầu vào chỉ được đọc từ tam giác dưới/trên của a, tuỳ thuộc vào giá trị của lower. Các giá trị của tam giác khác sẽ bị bỏ qua. Dữ liệu đầu ra được trả về trong cùng một tam giác; các giá trị trong tam giác khác được xác định triển khai và có thể là bất kỳ giá trị nào.
Nếu thứ hạng của a và b lớn hơn 2, thì các thứ hạng này được coi là các lô ma trận, trong đó tất cả các kích thước ngoại trừ 2 kích thước phụ đều là kích thước lô. a và b phải có các phương diện lô bằng nhau.
Tập hợp
Xem thêm XlaBuilder::Tuple.
Một bộ dữ liệu chứa nhiều xử lý dữ liệu có thể thay đổi, mỗi bộ xử lý có hình dạng riêng.
Điều này tương tự như std::tuple trong C++. Về mặt khái niệm:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
Bạn có thể phân tích cú pháp (truy cập) các bộ dữ liệu thông qua toán tử GetTupleElement.
Mặc dù
Hãy xem thêm XlaBuilder::While.
While(condition, body, init)
| Đối số | Loại | Ngữ nghĩa |
|---|---|---|
condition |
XlaComputation |
Tính toán XlaComputation thuộc loại T -> PRED xác định điều kiện kết thúc của vòng lặp. |
body |
XlaComputation |
XlaComputation thuộc loại T -> T xác định phần nội dung của vòng lặp. |
init |
T |
Giá trị ban đầu cho thông số của condition và body. |
Thực thi tuần tự body cho đến khi condition không thành công. Điều này tương tự như một vòng lặp while thông thường trong nhiều ngôn ngữ khác, ngoại trừ các điểm khác biệt và hạn chế được liệt kê bên dưới.
- Nút
Whiletrả về một giá trị thuộc loạiT, là kết quả của lần thực thibodygần đây nhất. - Hình dạng của loại
Tđược xác định cố định và phải giống nhau trên tất cả các lần lặp.
Các tham số T của phép tính được khởi tạo bằng giá trị init trong lần lặp đầu tiên và tự động cập nhật thành kết quả mới từ body trong mỗi lần lặp tiếp theo.
Một trường hợp sử dụng chính của nút While là triển khai việc thực thi lặp lại quá trình huấn luyện trong mạng nơron. Mã giả lập đơn giản được hiển thị bên dưới cùng với biểu đồ thể hiện phép tính. Bạn có thể tìm thấy mã này trong while_test.cc.
Loại T trong ví dụ này là Tuple bao gồm int32 cho số lần lặp và vector[10] cho tích luỹ. Đối với 1000 lần lặp, vòng lặp này sẽ tiếp tục thêm một vectơ không đổi vào tích luỹ.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}