 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看 |
 在 Google Colab 中运行 在 Google Colab 中运行 |
 View source on GitHub View source on GitHub |
 Download notebook Download notebook |
概述
此笔记本将演示如何使用权重归一化层以及如何提升收敛。
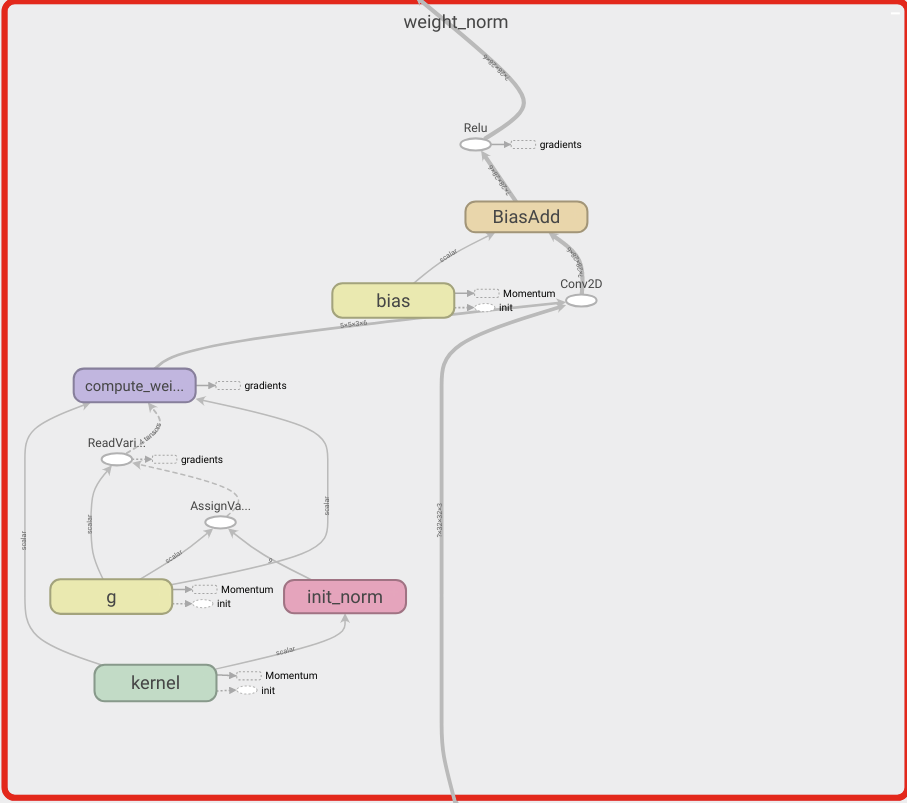
WeightNormalization
用于加速深度神经网络训练的一个简单的重新参数化:
Tim Salimans、Diederik P. Kingma (2016)
通过以这种方式重新参数化权重,我们改善了优化问题的条件,并加快了随机梯度下降的收敛速度。我们的重新参数化受到批次归一化的启发,但没有在 minibatch 中的样本之间引入任何依赖关系。这意味着我们的方法也可以成功应用于循环模型(例如 LSTM)和对噪声敏感的应用(例如深度强化学习或生成模型),而批次归一化则不太适合这类模型和应用。尽管我们的方法要简单得多,但它仍可以在很大程度上为完整批次归一化提供加速。另外,我们的方法计算开销较低,从而可以在相同的时间内执行更多优化步骤。
设置
pip install -q -U tensorflow-addonsimport tensorflow as tf
import tensorflow_addons as tfa
import numpy as np
from matplotlib import pyplot as plt
# Hyper Parameters
batch_size = 32
epochs = 10
num_classes=10
构建模型
# Standard ConvNet
reg_model = tf.keras.Sequential([
tf.keras.layers.Conv2D(6, 5, activation='relu'),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Conv2D(16, 5, activation='relu'),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(120, activation='relu'),
tf.keras.layers.Dense(84, activation='relu'),
tf.keras.layers.Dense(num_classes, activation='softmax'),
])
# WeightNorm ConvNet
wn_model = tf.keras.Sequential([
tfa.layers.WeightNormalization(tf.keras.layers.Conv2D(6, 5, activation='relu')),
tf.keras.layers.MaxPooling2D(2, 2),
tfa.layers.WeightNormalization(tf.keras.layers.Conv2D(16, 5, activation='relu')),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Flatten(),
tfa.layers.WeightNormalization(tf.keras.layers.Dense(120, activation='relu')),
tfa.layers.WeightNormalization(tf.keras.layers.Dense(84, activation='relu')),
tfa.layers.WeightNormalization(tf.keras.layers.Dense(num_classes, activation='softmax')),
])
加载数据
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
# Convert class vectors to binary class matrices.
y_train = tf.keras.utils.to_categorical(y_train, num_classes)
y_test = tf.keras.utils.to_categorical(y_test, num_classes)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
Downloading data from https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz 170500096/170498071 [==============================] - 6s 0us/step
训练模型
reg_model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
reg_history = reg_model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
Epoch 1/10 1563/1563 [==============================] - 5s 3ms/step - loss: 1.6481 - accuracy: 0.3959 - val_loss: 1.5032 - val_accuracy: 0.4505 Epoch 2/10 1563/1563 [==============================] - 4s 3ms/step - loss: 1.3405 - accuracy: 0.5207 - val_loss: 1.2814 - val_accuracy: 0.5434 Epoch 3/10 1563/1563 [==============================] - 4s 3ms/step - loss: 1.2279 - accuracy: 0.5627 - val_loss: 1.2407 - val_accuracy: 0.5507 Epoch 4/10 1563/1563 [==============================] - 4s 3ms/step - loss: 1.1465 - accuracy: 0.5939 - val_loss: 1.2135 - val_accuracy: 0.5650 Epoch 5/10 1563/1563 [==============================] - 4s 3ms/step - loss: 1.0887 - accuracy: 0.6156 - val_loss: 1.1859 - val_accuracy: 0.5871 Epoch 6/10 1563/1563 [==============================] - 4s 3ms/step - loss: 1.0320 - accuracy: 0.6338 - val_loss: 1.1298 - val_accuracy: 0.6070 Epoch 7/10 1563/1563 [==============================] - 4s 3ms/step - loss: 0.9882 - accuracy: 0.6486 - val_loss: 1.1232 - val_accuracy: 0.6112 Epoch 8/10 1563/1563 [==============================] - 4s 3ms/step - loss: 0.9439 - accuracy: 0.6669 - val_loss: 1.1192 - val_accuracy: 0.6120 Epoch 9/10 1563/1563 [==============================] - 4s 3ms/step - loss: 0.9070 - accuracy: 0.6784 - val_loss: 1.1235 - val_accuracy: 0.6168 Epoch 10/10 1563/1563 [==============================] - 4s 3ms/step - loss: 0.8794 - accuracy: 0.6892 - val_loss: 1.1383 - val_accuracy: 0.6184
wn_model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
wn_history = wn_model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
Epoch 1/10 1563/1563 [==============================] - 8s 5ms/step - loss: 1.5910 - accuracy: 0.4199 - val_loss: 1.3740 - val_accuracy: 0.5097 Epoch 2/10 1563/1563 [==============================] - 7s 5ms/step - loss: 1.3134 - accuracy: 0.5292 - val_loss: 1.2580 - val_accuracy: 0.5454 Epoch 3/10 1563/1563 [==============================] - 7s 4ms/step - loss: 1.1945 - accuracy: 0.5743 - val_loss: 1.2153 - val_accuracy: 0.5669 Epoch 4/10 1563/1563 [==============================] - 7s 4ms/step - loss: 1.1125 - accuracy: 0.6043 - val_loss: 1.1817 - val_accuracy: 0.5820 Epoch 5/10 1563/1563 [==============================] - 7s 4ms/step - loss: 1.0498 - accuracy: 0.6264 - val_loss: 1.1949 - val_accuracy: 0.5805 Epoch 6/10 1563/1563 [==============================] - 7s 4ms/step - loss: 0.9947 - accuracy: 0.6477 - val_loss: 1.1413 - val_accuracy: 0.5956 Epoch 7/10 1563/1563 [==============================] - 7s 4ms/step - loss: 0.9514 - accuracy: 0.6634 - val_loss: 1.1308 - val_accuracy: 0.6085 Epoch 8/10 1563/1563 [==============================] - 7s 4ms/step - loss: 0.9040 - accuracy: 0.6810 - val_loss: 1.1338 - val_accuracy: 0.6137 Epoch 9/10 1563/1563 [==============================] - 7s 4ms/step - loss: 0.8686 - accuracy: 0.6927 - val_loss: 1.1266 - val_accuracy: 0.6156 Epoch 10/10 1563/1563 [==============================] - 7s 4ms/step - loss: 0.8343 - accuracy: 0.7054 - val_loss: 1.1073 - val_accuracy: 0.6233
reg_accuracy = reg_history.history['accuracy']
wn_accuracy = wn_history.history['accuracy']
plt.plot(np.linspace(0, epochs, epochs), reg_accuracy,
color='red', label='Regular ConvNet')
plt.plot(np.linspace(0, epochs, epochs), wn_accuracy,
color='blue', label='WeightNorm ConvNet')
plt.title('WeightNorm Accuracy Comparison')
plt.legend()
plt.grid(True)
plt.show()

