Conozca lo último en aprendizaje automático, IA generativa y más en el
Simposio WiML 2023.
El Marco de Aprendizaje Estructurado Neural
Organiza tus páginas con colecciones
Guarda y categoriza el contenido según tus preferencias.
El aprendizaje estructurado neuronal (NSL) se enfoca en entrenar redes neuronales profundas aprovechando señales estructuradas (cuando están disponibles) junto con entradas de características. Como fue presentado por Bui et al. (WSDM'18) , estas señales estructuradas se utilizan para regularizar el entrenamiento de una red neuronal, obligando al modelo a aprender predicciones precisas (al minimizar la pérdida supervisada), mientras que al mismo tiempo se mantiene la similitud estructural de entrada (al minimizar la pérdida del vecino). , consulte la figura a continuación). Esta técnica es genérica y se puede aplicar en arquitecturas neuronales arbitrarias (como NN de avance, NN convolucionales y NN recurrentes).
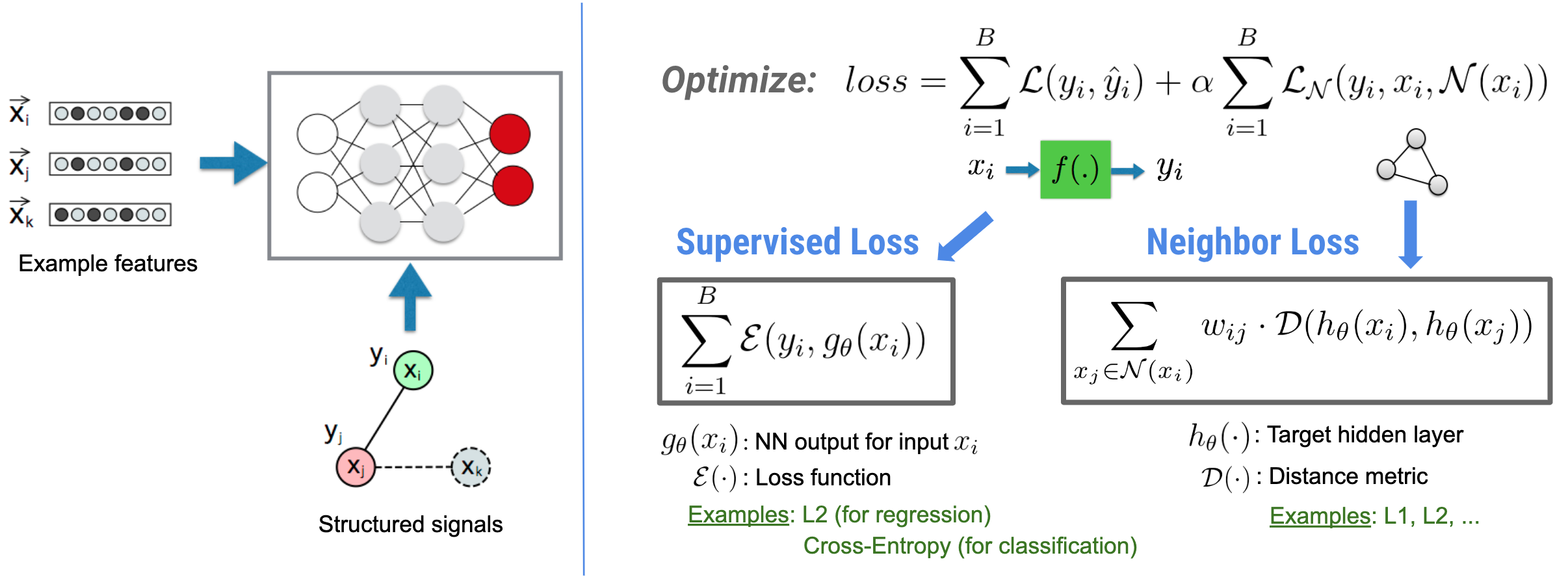
Tenga en cuenta que la ecuación de pérdida de vecino generalizada es flexible y puede tener otras formas además de la ilustrada arriba. Por ejemplo, también podemos seleccionar\(\sum_{x_j \in \mathcal{N}(x_i)}\mathcal{E}(y_i,g_\theta(x_j))\) para que sea la pérdida del vecino, que calcula la distancia entre la verdad del terreno \(y_i\)y la predicción del vecino \(g_\theta(x_j)\). Esto se usa comúnmente en el aprendizaje contradictorio (Goodfellow et al., ICLR'15) . Por lo tanto, NSL generaliza a Neural Graph Learning si los vecinos están representados explícitamente por un gráfico, y a Adversarial Learning si los vecinos son inducidos implícitamente por una perturbación adversaria.
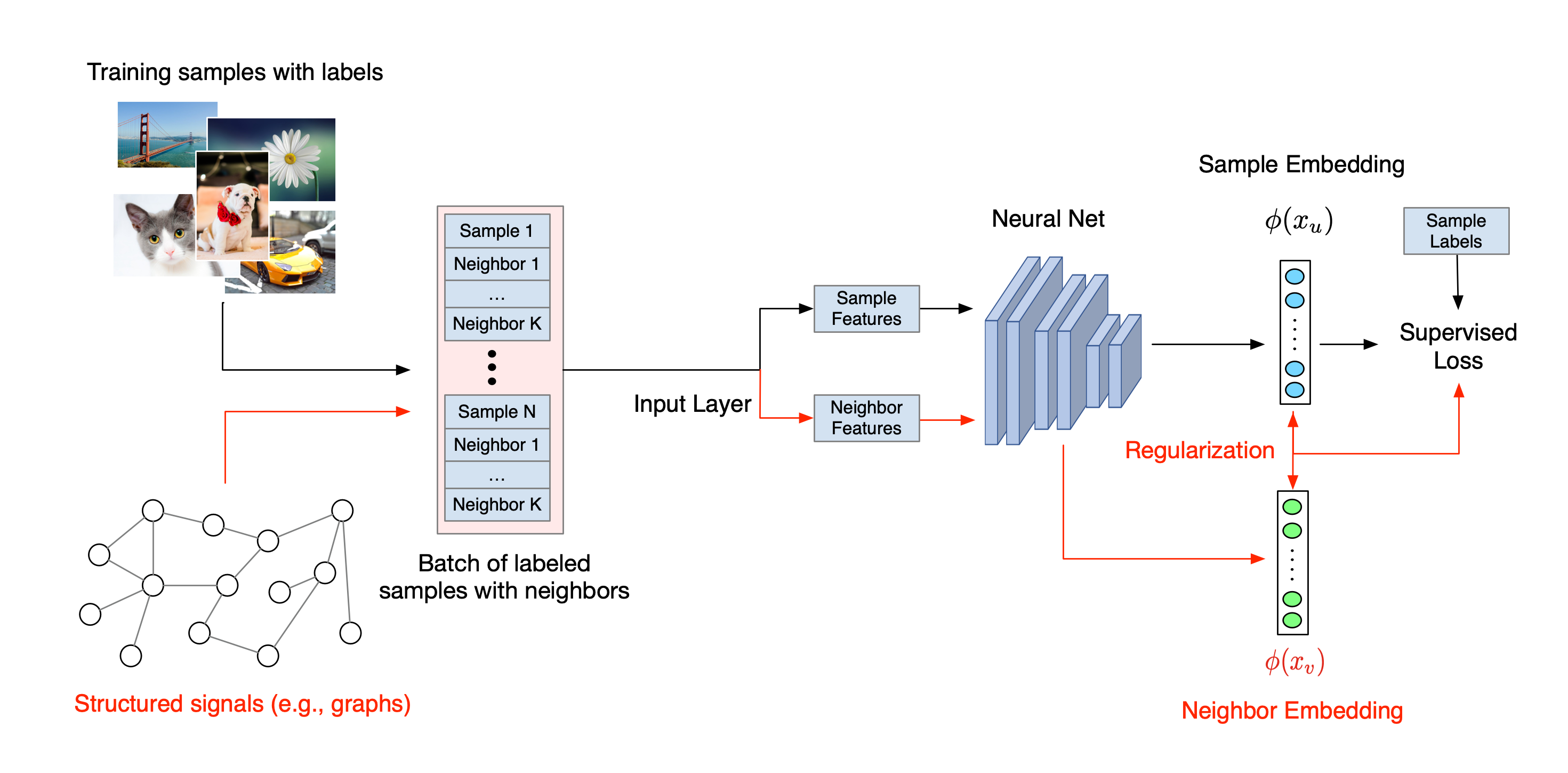
El flujo de trabajo general para el aprendizaje estructurado neuronal se ilustra a continuación. Las flechas negras representan el flujo de trabajo de entrenamiento convencional y las flechas rojas representan el nuevo flujo de trabajo introducido por NSL para aprovechar las señales estructuradas. Primero, las muestras de entrenamiento se aumentan para incluir señales estructuradas. Cuando las señales estructuradas no se proporcionan explícitamente, pueden construirse o inducirse (esto último se aplica al aprendizaje por confrontación). A continuación, las muestras de entrenamiento aumentadas (incluidas las muestras originales y sus vecinos correspondientes) se envían a la red neuronal para calcular sus incrustaciones. La distancia entre el empotramiento de una muestra y el empotramiento de su vecino se calcula y se usa como la pérdida del vecino, que se trata como un término de regularización y se agrega a la pérdida final. Para la regularización explícita basada en vecinos, generalmente calculamos la pérdida de vecinos como la distancia entre la incrustación de la muestra y la incrustación del vecino. Sin embargo, se puede usar cualquier capa de la red neuronal para calcular la pérdida del vecino. Por otro lado, para la regularización basada en vecinos inducidos (contradictorio), calculamos la pérdida del vecino como la distancia entre la predicción de salida del vecino contradictorio inducido y la etiqueta de verdad del terreno.
¿Por qué usar NSL?
NSL trae las siguientes ventajas:
- Mayor precisión : la(s) señal(es) estructurada(s) entre las muestras puede proporcionar información que no siempre está disponible en las entradas de características; por lo tanto, se ha demostrado que el enfoque de entrenamiento conjunto (con características y señales estructuradas) supera a muchos métodos existentes (que se basan en el entrenamiento solo con características) en una amplia gama de tareas, como la clasificación de documentos y la clasificación de intención semántica ( Bui et al. ., WSDM'18 & Kipf et al., ICLR'17 ).
- Robustez : se ha demostrado que los modelos entrenados con ejemplos adversarios son robustos frente a perturbaciones adversarias diseñadas para confundir la predicción o clasificación de un modelo ( Goodfellow et al., ICLR'15 & Miyato et al., ICLR'16 ). Cuando el número de muestras de entrenamiento es pequeño, el entrenamiento con ejemplos adversarios también ayuda a mejorar la precisión del modelo ( Tsipras et al., ICLR'19 ).
- Se requieren menos datos etiquetados : NSL permite que las redes neuronales aprovechen los datos etiquetados y no etiquetados, lo que extiende el paradigma de aprendizaje al aprendizaje semisupervisado . Específicamente, NSL permite que la red se entrene utilizando datos etiquetados como en el entorno supervisado y, al mismo tiempo, impulsa a la red a aprender representaciones ocultas similares para las "muestras vecinas" que pueden o no tener etiquetas. Esta técnica se ha mostrado muy prometedora para mejorar la precisión del modelo cuando la cantidad de datos etiquetados es relativamente pequeña ( Bui et al., WSDM'18 & Miyato et al., ICLR'16 ).
Tutoriales paso a paso
Para obtener experiencia práctica con el aprendizaje estructurado neuronal, tenemos tutoriales que cubren varios escenarios donde las señales estructuradas se pueden dar, construir o inducir explícitamente. Aquí hay algunos:
Se pueden encontrar más ejemplos y tutoriales en el directorio de ejemplos de nuestro repositorio de GitHub.
Salvo que se indique lo contrario, el contenido de esta página está sujeto a la licencia Atribución 4.0 de Creative Commons, y los ejemplos de código están sujetos a la licencia Apache 2.0. Para obtener más información, consulta las políticas del sitio de Google Developers. Java es una marca registrada de Oracle o sus afiliados.
Última actualización: 2021-11-17 (UTC)
[null,null,["Última actualización: 2021-11-17 (UTC)"],[],[],null,["# The Neural Structured Learning Framework\n\nNeural Structured Learning (NSL) focuses on training deep neural networks by\nleveraging structured signals (when available) along with feature inputs. As\nintroduced by [Bui et al. (WSDM'18)](https://research.google/pubs/pub46568.pdf),\nthese structured signals are used to regularize the training of a neural\nnetwork, forcing the model to learn accurate predictions (by minimizing\nsupervised loss), while at the same time maintaining the input structural\nsimilarity (by minimizing the neighbor loss, see the figure below). This\ntechnique is generic and can be applied on arbitrary neural architectures (such\nas Feed-forward NNs, Convolutional NNs and Recurrent NNs).\n\nNote that the generalized neighbor loss equation is flexible and can have other\nforms besides the one illustrated above. For example, we can also select\n\\\\(\\\\sum_{x_j \\\\in \\\\mathcal{N}(x_i)}\\\\mathcal{E}(y_i,g_\\\\theta(x_j))\\\\) to be the\nneighbor loss, which calculates the distance between the ground truth \\\\(y_i\\\\)\nand the prediction from the neighbor \\\\(g_\\\\theta(x_j)\\\\). This is commonly used in\nadversarial learning\n[(Goodfellow et al., ICLR'15)](https://arxiv.org/pdf/1412.6572.pdf). Therefore,\nNSL generalizes to **Neural Graph Learning** if neighbors are explicitly\nrepresented by a graph, and to **Adversarial Learning** if neighbors are\nimplicitly induced by adversarial perturbation.\n\nThe overall workflow for Neural Structured Learning is illustrated below. Black\narrows represent the conventional training workflow and red arrows represent the\nnew workflow as introduced by NSL to leverage structured signals. First, the\ntraining samples are augmented to include structured signals. When structured\nsignals are not explicitly provided, they can be either constructed or induced\n(the latter applies to adversarial learning). Next, the augmented training\nsamples (including both original samples and their corresponding neighbors) are\nfed to the neural network for calculating their embeddings. The distance between\na sample's embedding and its neighbor's embedding is calculated and used as the\nneighbor loss, which is treated as a regularization term and added to the final\nloss. For explicit neighbor-based regularization, we typically compute the\nneighbor loss as the distance between the sample's embedding and the neighbor's\nembedding. However, any layer of the neural network may be used to compute the\nneighbor loss. On the other hand, for induced neighbor-based regularization\n(adversarial), we compute the neighbor loss as the distance between the output\nprediction of the induced adversarial neighbor and the ground truth label.\n\nWhy use NSL?\n------------\n\nNSL brings the following advantages:\n\n- **Higher accuracy** : the structured signal(s) among samples can provide information that is not always available in feature inputs; therefore, the joint training approach (with both structured signals and features) has been shown to outperform many existing methods (that rely on training with features only) on a wide range of tasks, such as document classification and semantic intent classification ([Bui et al., WSDM'18](https://research.google/pubs/pub46568.pdf) \\& [Kipf et al., ICLR'17](https://arxiv.org/pdf/1609.02907.pdf)).\n- **Robustness** : models trained with adversarial examples have been shown to be robust against adversarial perturbations designed for misleading a model's prediction or classification ([Goodfellow et al., ICLR'15](https://arxiv.org/pdf/1412.6572.pdf) \\& [Miyato et al., ICLR'16](https://arxiv.org/pdf/1704.03976.pdf)). When the number of training samples is small, training with adversarial examples also helps improve model accuracy ([Tsipras et al., ICLR'19](https://arxiv.org/pdf/1805.12152.pdf)).\n- **Less labeled data required** : NSL enables neural networks to harness both labeled and unlabeled data, which extends the learning paradigm to [semi-supervised learning](https://en.wikipedia.org/wiki/Semi-supervised_learning). Specifically, NSL allows the network to train using labeled data as in the supervised setting, and at the same time drives the network to learn similar hidden representations for the \"neighboring samples\" that may or may not have labels. This technique has shown great promise for improving model accuracy when the amount of labeled data is relatively small ([Bui et al., WSDM'18](https://research.google/pubs/pub46568.pdf) \\& [Miyato et al., ICLR'16](https://arxiv.org/pdf/1704.03976.pdf)).\n\nStep-by-step Tutorials\n----------------------\n\nTo obtain hands-on experience with Neural Structured Learning, we have tutorials\nthat cover various scenarios where structured signals may be explicitly given,\nconstructed, or induced. Here are a few:\n\n- [Graph regularization for document classification using natural graphs](/neural_structured_learning/tutorials/graph_keras_mlp_cora).\n In this tutorial, we explore the use of graph regularization to classify\n documents that form a natural (organic) graph.\n\n- [Graph regularization for sentiment classification using synthesized graphs](/neural_structured_learning/tutorials/graph_keras_lstm_imdb).\n In this tutorial, we demonstrate the use of graph regularization to classify\n movie review sentiments by constructing (synthesizing) structured signals.\n\n- [Adversarial learning for image classification](/neural_structured_learning/tutorials/adversarial_keras_cnn_mnist).\n In this tutorial, we explore the use of adversarial learning (where\n structured signals are induced) to classify images containing numeric\n digits.\n\nMore examples and tutorials can be found in the\n[examples](https://github.com/tensorflow/neural-structured-learning/tree/master/neural_structured_learning/examples)\ndirectory of our GitHub repository."]]
