Эта страница переведена с помощью Cloud Translation API.

Вероятностное программирование в Oryx

Посмотреть на TensorFlow.org

Запускаем в Google Colab

Посмотреть исходный код на GitHub

Скачать блокнот

pip install -q -U jax jaxlib
pip install -q -Uq oryx -I
pip install -q tfp-nightly --upgrade

from functools import partial

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')

import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random

from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions

import oryx

Вероятностное программирование - это идея о том, что мы можем выразить вероятностные модели, используя функции языка программирования. Такие задачи, как байесовский вывод или маргинализация, затем предоставляются в виде языковых функций и потенциально могут быть автоматизированы.

Oryx предоставляет систему вероятностного программирования, в которой вероятностные программы просто выражаются как функции Python; затем эти программы преобразуются с помощью преобразований составных функций, как в JAX! Идея состоит в том, чтобы начать с простых программ (таких как выборка из случайной нормали) и скомпоновать их вместе, чтобы сформировать модели (например, байесовскую нейронную сеть). Важным моментом дизайна PPL Oryx является для того, чтобы программы , чтобы выглядеть как функции , которые вы бы уже писать и использовать в JAX, но аннотированный сделать преобразования осведомлены о них.

Давайте сначала импортируем основную функциональность Oryx PPL.

from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest

Что такое вероятностные программы в Oryx?

В Oryx вероятностные программы - это просто чистые функции Python, которые работают со значениями JAX и псевдослучайными ключами и возвращают случайную выборку. По замыслу, они совместимы с преобразованиями , как jit и vmap . Тем не менее, Oryx вероятностная система программирования предоставляет инструменты , которые позволяют аннотировать функции полезными способами.

Следуя философию JAX чистых функций, вероятностная программа Oryx является функцией Python , который принимает JAX PRNGKey в качестве первого аргумента и любого числа последующих аргументов кондиционирования. Выход функции называется «образец» и те же ограничения , которые применяются к jit -ed и vmap -ED функции применяются к вероятностным программ (например , отсутствие потока данных в зависимости от управления, без каких - либо побочных эффектов, и т.д.). Это отличается от многих систем императивного вероятностного программирования, в которых «образец» представляет собой всю трассировку выполнения, включая значения, внутренние для выполнения программы. Позже мы увидим , как Oryx может получить доступ к внутренним значению с помощью joint_sample , обсуждаемой ниже.

Program :: PRNGKey -> ... -> Sample

Вот программа «привет мир» , что образцы из логарифмически нормального распределения .

def log_normal(key):
  return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))

print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
0.8139614
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

PNG

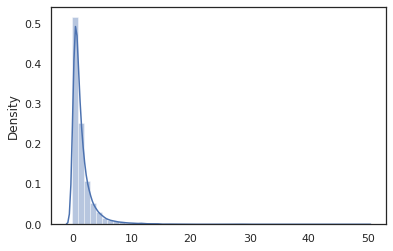
log_normal функция представляет собой тонкую оболочку вокруг Tensorflow Вероятность (TFP) распределения, но вместо вызова tfd.Normal(0., 1.).sample , мы использовали random_variable вместо этого. Как мы увидим позже, random_variable позволяет преобразовывать объекты в вероятностные программы, наряду с другой полезной функциональностью.

Мы можем преобразовать log_normal в функцию логарифма плотности с помощью log_prob преобразования:

print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()

-0.9189385

PNG

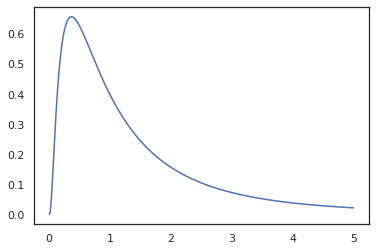
Поскольку мы аннотированный функцию с random_variable , log_prob знает , что есть вызов tfd.Normal(0., 1.).sample и использует tfd.Normal(0., 1.).log_prob вычислить распределение базы журнал проб. Для обработки jnp.exp , ppl.log_prob автоматически вычисляет плотность через биективные функции, отслеживание изменений объема в переключающего из переменных вычислений.

В Oryx, мы можем принять программы и преобразовывать их с помощью функции преобразования - например, jax.jit или log_prob . Однако Oryx не может сделать это с помощью любой программы; для этого требуются функции выборки, которые зарегистрировали свою функцию плотности бревен в Oryx. К счастью, Oryx автоматически регистрирует TensorFlow вероятности (TFP) распределений в своей системе.

Инструменты вероятностного программирования Oryx

В Oryx есть несколько преобразований функций, направленных на вероятностное программирование. Мы рассмотрим большинство из них и приведем несколько примеров. В конце мы объединим все это в тематическое исследование MCMC. Вы можете также обратиться к документации по core.ppl.transformations для получения более подробной информации.

`random_variable`

random_variable имеет две основные функциональные части, и сосредоточены на аннотирования функции Python с информацией , которая может быть использована в преобразованиях.

random_variable 'работает как тождественная функция по умолчанию, но можно использовать регистрацию типа , характерную для объектов преобразовывают в вероятностную programs.`
Для ГОО типов (функций Python, лямбды, functools.partial с, и т.д.) и произвольный object s (как JAX DeviceArray s) будет просто вернуть свой вклад.
```
random_variable(x: object) == x
random_variable(f: Callable[...]) == f
```
Oryx автоматически регистрирует TensorFlow Вероятность (TFP) распределения, которые превращаются в вероятностные программы , которые требуют дистрибутива sample метода.
```
random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235
```
Oryx дополнительно встраивает информацию о распределении TFP в трассировки JAX, что позволяет автоматически вычислять плотность журналов.
random_variable значение может теги с именами, что делает их полезными для последующих преобразований, предоставляя дополнительное name аргумента ключевого слова для random_variable . Когда мы передаем массив в random_variable вместе с name (например , random_variable(x, name='x') ), он просто помечает значение и возвращает его. Если мы переходим в отзывной или распределения TFP, random_variable возвращает программу , которая теги его выходных данных с name .

Эти комментарии не меняют семантику программы при выполнении, но только при преобразовании (т.е. программа будет возвращать одинаковое значение с или без использования random_variable ).

Давайте рассмотрим пример, в котором мы используем обе функциональные возможности вместе.

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

В этой программе мы помеченные промежуточные продукты z и x , что делает преобразование joint_sample , intervene , conditional и graph_replace известны имена 'z' и 'x' . Позже мы подробно рассмотрим, как каждое преобразование использует имена.

`log_prob`

log_prob функция преобразования преобразует вероятностный программу Орикс в своей функции логарифмически плотности. Эта функция логарифмической плотности принимает потенциальную выборку из программы в качестве входных данных и возвращает ее логарифмическую плотность в соответствии с нижележащим распределением выборки.

log_prob :: Program -> (Sample -> LogDensity)

Как random_variable , он работает через реестр типов , где распределения TFP автоматически регистрируются, так log_prob(tfd.Normal(0., 1.)) называет tfd.Normal(0., 1.).log_prob . Для функций Python, однако, log_prob прослеживает программу с использованием JAX и внешнего вида для отбора заявлений. log_prob преобразование работает на большинстве программ , которые возвращают случайные величины, непосредственно или через обратимые преобразования , но не на программах, выборочные значения внутренне, которые не возвращаются. Если он не может инвертировать необходимые операции в программе, log_prob выдаст ошибку.

Вот некоторые примеры log_prob применительно к различным программам.

log_prob работает по программам , которые непосредственно выборки из распределений TFP (или других зарегистрированных типов) и возвращают их значение.

def normal(key):
  return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))

-0.9189385

log_prob способен вычислять лог-плотность образцов из программ , которые преобразуют случайные переменные , используя биективную функции (например , jnp.exp , jnp.tanh , jnp.split ).

def log_normal(key):
  return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))

-1.159165

Для того , чтобы вычислить выборку из log_normal «s журнал плотности, мы в первую очередь необходимо , чтобы инвертировать exp , взяв log образца, а затем добавить коррекцию объемного изменения , используя обратный лог-йе якобиан exp (см изменения переменной формулы из Википедии).

log_prob работа с программами, выводящие структурам образцов нравятся, словари Python или кортежи.

def normal_2d(key):
  x = random_variable(
    tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
  x1, x2 = jnp.split(x, 2, 0)
  return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))

{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546

log_prob ходит по прослежены вычисления графика функции, вычисление прямых и обратных значений (и их лог-DET якобианы) при необходимости в попытку подключения возвращаемых значений с их базовыми значениями выборок с помощью хорошо определенной замены переменных. Возьмем следующий пример программы:

def complex_program(key):
  k1, k2 = random.split(key)
  z = random_variable(tfd.Normal(0., 1.))(k1)
  x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
  return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))

(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32))
-1.0967848

В этой программе, мы выборочная x условно на z , то есть мы нуждаются в значении z , прежде чем мы можем вычислить логарифмическую плотность x . Однако для того, чтобы вычислить z , мы должны сначала инвертировать jnp.exp применяется к z . Таким образом, для того , чтобы вычислить лог-плотность x и z , log_prob необходимо сначала инвертный первый выход, а затем передать его вперед через jax.nn.relu , чтобы вычислить среднее значение p(x | z) .

Для получения дополнительной информации о log_prob , вы можете обратиться к core.interpreters.log_prob . В реализации, log_prob тесно основаны от inverse преобразования JAX; чтобы узнать больше о inverse см core.interpreters.inverse .

`joint_sample`

Для определения более сложных и интересных программ мы будем использовать некоторые скрытые случайные величины, то есть случайные величины с ненаблюдаемыми значениями. Обратимся к latent_normal программе , что образцы случайная величина z , который используется как среднее другой случайной величины x .

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

В этой программе, z латентно так , если бы мы просто называем latent_normal(random.PRNGKey(0)) мы не будем знать фактическое значение z , которое отвечает за формирование x .

joint_sample является преобразованием , которое превращает программу в другую программу , которая возвращает словарь отображения строк имен (теги) к их значениям. Для работы нам нужно убедиться, что мы помечаем скрытые переменные, чтобы они отображались в выходных данных преобразованной функции.

joint_sample(latent_normal)(random.PRNGKey(0))

{'x': DeviceArray(0.01873656, dtype=float32),
 'z': DeviceArray(0.14389044, dtype=float32)}

Обратите внимание , что joint_sample преобразования программы в другую программу , которая осуществляет выборку совместного распределения над его скрытых значений, так что мы можем в дальнейшем преобразовать ее. Для таких алгоритмов, как MCMC и VI, обычно вычисляют логарифмическую вероятность совместного распределения как часть процедуры вывода. log_prob(latent_normal) не работает , так как она требует маргинализируя из z , но мы можем использовать log_prob(joint_sample(latent_normal)) .

print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))

-50.03529
-5049.535

Поскольку это такой общий узор, Сернобык также имеет joint_log_prob преобразование , которое является только состав log_prob и joint_sample .

print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))

-50.03529
-5049.535

`block`

block преобразования принимает в программе и последовательности имен и возвращает программу , которая ведет себя одинаково , за исключением , что в последующих преобразований (как joint_sample ), предоставленные имена игнорируются. Пример , где block удобно преобразовывает совместное распределение в течение до скрытого переменных «блокирующих» значений выборок в вероятности. Например, возьмем latent_normal , который сначала рисует z ~ N(0, 1) Тогда x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) это программа , которая скрывает x имя, так что если мы делаем joint_sample(block(latent_normal, names=['x'])) , мы получим словарь с только z в нем .

blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))

{'z': DeviceArray(0.14389044, dtype=float32)}

`intervene`

intervene преобразование затирает образцы в вероятностном программе со значениями извне. Возвращаясь к нашей latent_normal программы, скажем , мы были заинтересованы в выполнении того же программы , но хотел z быть закреплен на 4. Вместо того , писать новую программу, мы можем использовать intervene , чтобы переопределить значение z .

intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();

/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

PNG

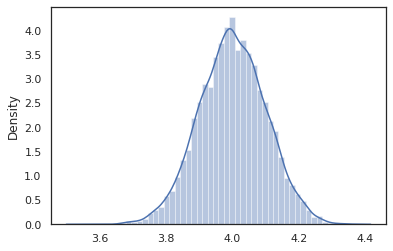
В intervened образцы функции от p(x | do(z = 4)) , который просто стандартное нормальное распределение с центром в точке 4. Когда мы intervene на определенное значение, это значение больше не считаются случайной величиной. Это означает , что z значение не будет помеченных при выполнении intervened .

`conditional`

conditional преобразования программа , которая скрыты образцы значений в одно , что условия на этих скрытых значениях. Возвращаясь к нашей latent_normal программы, образцы p(x) с латентным z , мы можем превратить его в условную программе p(x | z) .

cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()

99.87485
49.874847
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

PNG

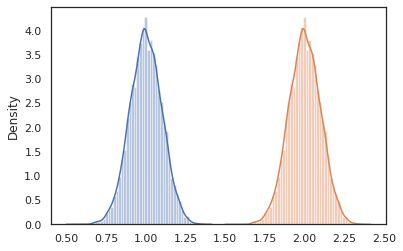
`nest`

Когда мы начинаем составлять вероятностные программы для создания более сложных, обычно повторно используются функции, имеющие некоторую важную логику. Например, если мы хотим построить байесовскую нейронную сеть, может быть важной dense программой, образцы весов и выполняет прямой проход.

Если мы повторно функция, однако, мы могли бы в конечном итоге с повторяющимися помеченными значениями в конечной программе, которая запрещенное преобразованиями как joint_sample . Мы можем использовать nest , чтобы создать тег «прицелы» , где любые образцы внутри именованного объем будут вставлены в гнездовой словарь.

def f(key):
  return random_variable(tfd.Normal(0., 1.), name='x')(key)

def g(key):
  k1, k2 = random.split(key)
  return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))

{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
 'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }

Пример использования: байесовская нейронная сеть

Давайте попробовать нашу руку на обучение нейронной сети байесовской классификации классического Fisher Iris набор данных. Он относительно небольшой и малоразмерный, поэтому мы можем попробовать напрямую отобрать апостериорные зубы с помощью MCMC.

Во-первых, давайте импортируем набор данных и некоторые дополнительные утилиты из Oryx.

from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']

num_features = features.shape[-1]
num_classes = len(iris.target_names)

from oryx.experimental import mcmc
from oryx.util import summary, get_summaries

Мы начинаем с создания плотного слоя, который будет иметь нормальные априорные значения по весам и смещению. Для этого мы сначала определим dense функцию высшего порядка , которая принимает в желаемом выходе измерения и активации функции. dense функция возвращает вероятностную программу , которая представляет собой условное распределение p(h | x) , где h является выходом из плотного слоя и x является его вводом. Она первые образцы вес и смещение , а затем применяют их к x .

def dense(dim_out, activation=jax.nn.relu):
  def forward(key, x):
    dim_in = x.shape[-1]
    w_key, b_key = random.split(key)
    w = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
          name='w')(w_key)
    b = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
          name='b')(b_key)
    return activation(jnp.dot(w, x) + b)
  return forward

Для того, чтобы составить несколько dense слоев вместе, мы будем реализовывать mlp (многослойный персептрон) функцию высшего порядка , который принимает в списке скрытых размеров и числа классов. Она возвращает программу , которая неоднократно называют dense , используя соответствующий hidden_size и , наконец , возвращает логит для каждого класса в конечном слое. Обратите внимание на использование nest , которое создает имя области для каждого слоя.

def mlp(hidden_sizes, num_classes):
  num_hidden = len(hidden_sizes)
  def forward(key, x):
    keys = random.split(key, num_hidden + 1)
    for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
      x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
    logits = nest(dense(num_classes, activation=lambda x: x),
                  scope=f'layer_{num_hidden + 1}')(keys[-1], x)
    return logits
  return forward

Чтобы реализовать полную модель, нам нужно смоделировать метки как категориальные случайные величины. Мы определим predict функцию , которая принимает в наборе данных xs (в особенности) , которые затем пропускают в mlp с помощью vmap . Когда мы используем vmap(partial(mlp, mlp_key)) , в выборку один набор весов, но карта прямой проход через все входные xs . Это производит набор logits , которые параметризуют независимые категориальные распределения.

def predict(mlp):
  def forward(key, xs):
    mlp_key, label_key = random.split(key)
    logits = vmap(partial(mlp, mlp_key))(xs)
    return random_variable(
        tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
  return forward

Это полная модель! Давайте использовать MCMC для выборки апостериорных весов BNN для заданных данных; Сначала мы строим BNN «шаблон» с помощью mlp .

bnn = mlp([200, 200], num_classes)

Для того, чтобы построить начальную точку для нашей цепи Маркова, мы можем использовать joint_sample с входом фиктивной.

weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())

dict_keys(['layer_1', 'layer_2', 'layer_3'])

Вычисления вероятности журнала совместного распределения достаточно для многих алгоритмов вывода. Давайте теперь говорят , что мы наблюдаем x и хотим попробовать заднюю p(z | x) . Для сложных распределений, мы не будем иметь возможности изолировать из x (хотя для latent_normal мы можем) , но мы можем вычислить ненормализованный плотность лога log p(z, x) , где x прикреплен к определенному значению. Мы можем использовать ненормированную логарифмическую вероятность с MCMC для выборки апостериорного. Давайте напишем эту "закрепленную" функцию проверки журнала.

def target_log_prob(weights):
  return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)

Теперь мы можем использовать tfp.mcmc к образцу кзади , используя нашу ненормированную функцию плотности журнала. Обратите внимание , что мы должны использовать «сглаженную» версию наших вложенных весов словарь , чтобы быть совместимыми с tfp.mcmc , поэтому мы используем дерево утилиту Jax, чтобы расплющить и unflatten.

@jit
def run_chain(key, weights):
  flat_state, sample_tree = jax.tree_flatten(weights)

  def flat_log_prob(*states):
    return target_log_prob(jax.tree_unflatten(sample_tree, states))

  def trace_fn(_, results):
    return results.inner_results.accepted_results.target_log_prob

  flat_states, log_probs = tfp.mcmc.sample_chain(
    1000,
    num_burnin_steps=9000,
    kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
        tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
        9000, target_accept_prob=0.7),
    trace_fn=trace_fn,
    current_state=flat_state,
    seed=key)
  samples = jax.tree_unflatten(sample_tree, flat_states)
  return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)

plt.plot(log_probs)
plt.show()

PNG

Мы можем использовать наши образцы для оценки точности обучения с помощью усреднения байесовской модели (BMA). Чтобы вычислить его, мы можем использовать intervene с bnn к «Inject» заднего веса вместо тех, которые отбираемых из ключа. Для вычисления логита для каждой точки данных для каждого заднего образца, мы можем удвоить vmap над posterior_weights и features .

output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
    random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)

print('Average sample accuracy:', (
    output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
    output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())

Average sample accuracy: 0.9874067
BMA accuracy: 0.99333334

Вывод

В Oryx вероятностные программы - это просто функции JAX, которые принимают на вход (псевдо) случайность. Благодаря тесной интеграции Oryx с системой преобразования функций JAX, мы можем писать вероятностные программы и управлять ими так же, как мы пишем код JAX. В результате получается простая, но гибкая система для построения сложных моделей и выполнения логических выводов.