নিউরাল স্ট্রাকচার্ড লার্নিং ফ্রেমওয়ার্ক
সেভ করা পৃষ্ঠা গুছিয়ে রাখতে 'সংগ্রহ' ব্যবহার করুন
আপনার পছন্দ অনুযায়ী কন্টেন্ট সেভ করুন ও সঠিক বিভাগে রাখুন।
নিউরাল স্ট্রাকচার্ড লার্নিং (NSL) ফিচার ইনপুট সহ স্ট্রাকচার্ড সিগন্যাল (যখন উপলব্ধ) ব্যবহার করে গভীর নিউরাল নেটওয়ার্ককে প্রশিক্ষণের উপর ফোকাস করে। বুই এট আল দ্বারা প্রবর্তিত হিসাবে। (WSDM'18) , এই কাঠামোগত সংকেতগুলি একটি নিউরাল নেটওয়ার্কের প্রশিক্ষণকে নিয়মিত করতে ব্যবহৃত হয়, মডেলটিকে সঠিক ভবিষ্যদ্বাণী শিখতে বাধ্য করে (তত্ত্বাবধানে থাকা ক্ষতি কমিয়ে), একই সময়ে ইনপুট কাঠামোগত মিল বজায় রাখে (প্রতিবেশীর ক্ষতি কমিয়ে) , নীচের চিত্র দেখুন)। এই কৌশলটি জেনেরিক এবং নির্বিচারে নিউরাল আর্কিটেকচারে প্রয়োগ করা যেতে পারে (যেমন ফিড-ফরোয়ার্ড এনএন, কনভোলিউশনাল এনএন এবং পুনরাবৃত্ত এনএন)।
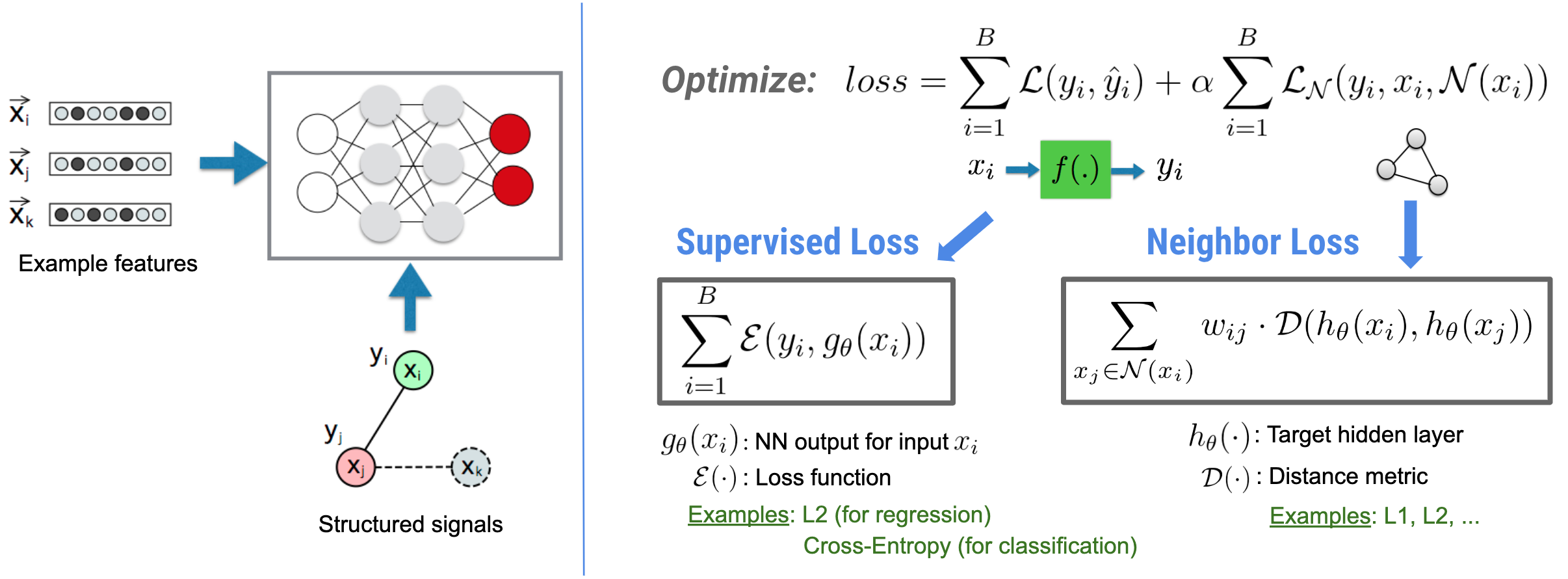
মনে রাখবেন যে সাধারণীকৃত প্রতিবেশী ক্ষতির সমীকরণটি নমনীয় এবং উপরে চিত্রিত একটি ছাড়াও অন্যান্য রূপ থাকতে পারে। উদাহরণস্বরূপ, আমরাও নির্বাচন করতে পারি\(\sum_{x_j \in \mathcal{N}(x_i)}\mathcal{E}(y_i,g_\theta(x_j))\) প্রতিবেশী ক্ষতি হতে হবে, যা স্থল সত্যের মধ্যে দূরত্ব গণনা করে \(y_i\)এবং প্রতিবেশীর কাছ থেকে ভবিষ্যদ্বাণী \(g_\theta(x_j)\). এটি সাধারণত প্রতিপক্ষ শিক্ষায় ব্যবহৃত হয় (গুডফেলো এট আল।, ICLR'15) । অতএব, এনএসএল নিউরাল গ্রাফ লার্নিংকে সাধারণীকরণ করে যদি প্রতিবেশীদের একটি গ্রাফ দ্বারা স্পষ্টভাবে প্রতিনিধিত্ব করা হয় এবং প্রতিবেশীরা যদি প্রতিকূলভাবে প্রতিকূলতা দ্বারা প্ররোচিত হয় তবে প্রতিপক্ষের শিক্ষার জন্য।
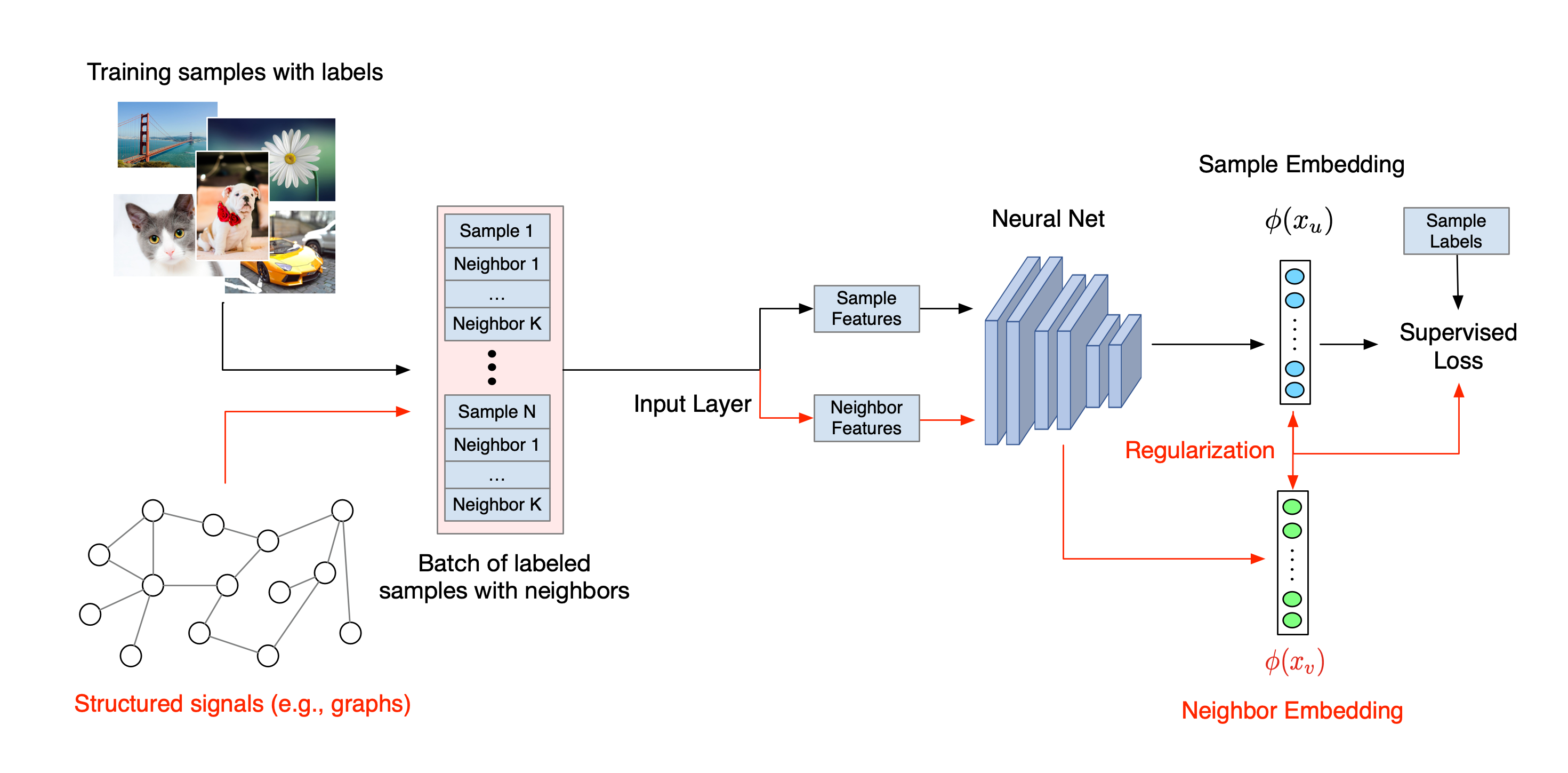
নিউরাল স্ট্রাকচার্ড লার্নিং এর সামগ্রিক কর্মপ্রবাহ নীচে চিত্রিত করা হয়েছে। কালো তীরগুলি প্রচলিত প্রশিক্ষণ কর্মপ্রবাহকে উপস্থাপন করে এবং লাল তীরগুলি কাঠামোগত সংকেতগুলিকে লিভারেজ করার জন্য NSL দ্বারা প্রবর্তিত নতুন কর্মপ্রবাহকে উপস্থাপন করে। প্রথমত, প্রশিক্ষণের নমুনাগুলিকে কাঠামোগত সংকেত অন্তর্ভুক্ত করার জন্য বর্ধিত করা হয়। যখন কাঠামোগত সংকেতগুলি স্পষ্টভাবে প্রদান করা হয় না, তখন সেগুলি হয় নির্মাণ বা প্ররোচিত করা যেতে পারে (পরবর্তীটি প্রতিপক্ষ শিক্ষার ক্ষেত্রে প্রযোজ্য)। এরপরে, বর্ধিত প্রশিক্ষণের নমুনাগুলি (মূল নমুনা এবং তাদের সংশ্লিষ্ট প্রতিবেশী উভয় সহ) তাদের এমবেডিং গণনা করার জন্য নিউরাল নেটওয়ার্কে খাওয়ানো হয়। একটি নমুনার এম্বেডিং এবং এর প্রতিবেশীর এম্বেডিংয়ের মধ্যে দূরত্ব গণনা করা হয় এবং প্রতিবেশীর ক্ষতি হিসাবে ব্যবহৃত হয়, যা একটি নিয়মিতকরণ শব্দ হিসাবে বিবেচিত হয় এবং চূড়ান্ত ক্ষতিতে যোগ করা হয়। সুস্পষ্ট প্রতিবেশী-ভিত্তিক নিয়মিতকরণের জন্য, আমরা সাধারণত প্রতিবেশীর ক্ষতিকে নমুনার এম্বেডিং এবং প্রতিবেশীর এম্বেডিংয়ের মধ্যে দূরত্ব হিসাবে গণনা করি। যাইহোক, নিউরাল নেটওয়ার্কের যে কোন স্তর প্রতিবেশী ক্ষতি গণনা করতে ব্যবহার করা যেতে পারে। অন্যদিকে, প্ররোচিত প্রতিবেশী-ভিত্তিক নিয়মিতকরণের জন্য (প্রতিপক্ষের), আমরা প্রতিবেশী ক্ষতিকে প্ররোচিত প্রতিপক্ষ প্রতিবেশীর আউটপুট পূর্বাভাস এবং গ্রাউন্ড ট্রুথ লেবেলের মধ্যে দূরত্ব হিসাবে গণনা করি।
কেন NSL ব্যবহার করবেন?
NSL নিম্নলিখিত সুবিধা নিয়ে আসে:
- উচ্চতর নির্ভুলতা : নমুনাগুলির মধ্যে কাঠামোগত সংকেত(গুলি) এমন তথ্য প্রদান করতে পারে যা বৈশিষ্ট্য ইনপুটগুলিতে সবসময় পাওয়া যায় না; তাই, যৌথ প্রশিক্ষণের পদ্ধতি (গঠিত সংকেত এবং বৈশিষ্ট্য উভয়ের সাথে) অনেকগুলি বিদ্যমান পদ্ধতিকে (যেগুলি শুধুমাত্র বৈশিষ্ট্যগুলির সাথে প্রশিক্ষণের উপর নির্ভর করে) বিস্তৃত কাজগুলিতে, যেমন নথির শ্রেণিবিন্যাস এবং শব্দার্থিক অভিপ্রায় শ্রেণীবিভাগ ( বুই এট আল ., WSDM'18 এবং Kipf et al., ICLR'17 )।
- দৃঢ়তা : প্রতিকূল উদাহরণ সহ প্রশিক্ষিত মডেলগুলি একটি মডেলের ভবিষ্যদ্বাণী বা শ্রেণীবিভাগকে বিভ্রান্ত করার জন্য ডিজাইন করা প্রতিকূল বিরক্তির বিরুদ্ধে শক্তিশালী বলে দেখানো হয়েছে ( Goodfellow et al., ICLR'15 এবং Miyato et al., ICLR'16 )। যখন প্রশিক্ষণের নমুনার সংখ্যা কম হয়, তখন প্রতিকূল উদাহরণ সহ প্রশিক্ষণও মডেলের নির্ভুলতা উন্নত করতে সাহায্য করে ( Tsipras et al., ICLR'19 )।
- কম লেবেলযুক্ত ডেটার প্রয়োজন : NSL নিউরাল নেটওয়ার্কগুলিকে লেবেলযুক্ত এবং লেবেলবিহীন উভয় ডেটা ব্যবহার করতে সক্ষম করে, যা শেখার দৃষ্টান্তকে আধা-তত্ত্বাবধানে শিক্ষার জন্য প্রসারিত করে। বিশেষভাবে, NSL নেটওয়ার্কটিকে তত্ত্বাবধানে থাকা সেটিং-এর মতো লেবেলযুক্ত ডেটা ব্যবহার করে প্রশিক্ষণের অনুমতি দেয় এবং একই সময়ে নেটওয়ার্কটিকে "প্রতিবেশী নমুনা" এর জন্য অনুরূপ লুকানো উপস্থাপনা শিখতে চালিত করে যেগুলির লেবেল থাকতে পারে বা নাও থাকতে পারে৷ এই কৌশলটি মডেল নির্ভুলতা উন্নত করার জন্য দুর্দান্ত প্রতিশ্রুতি দেখিয়েছে যখন লেবেলযুক্ত ডেটার পরিমাণ তুলনামূলকভাবে কম হয় ( Bui et al., WSDM'18 এবং Miyato et al., ICLR'16 )।
ধাপে ধাপে টিউটোরিয়াল
নিউরাল স্ট্রাকচার্ড লার্নিং এর সাথে অভিজ্ঞতা অর্জনের জন্য, আমাদের কাছে টিউটোরিয়াল রয়েছে যা বিভিন্ন পরিস্থিতিতে কভার করে যেখানে কাঠামোগত সংকেতগুলি স্পষ্টভাবে দেওয়া, তৈরি করা বা প্ররোচিত করা যেতে পারে। এখানে কয়েকটি আছে:
আরও উদাহরণ এবং টিউটোরিয়াল আমাদের GitHub সংগ্রহস্থলের উদাহরণ ডিরেক্টরিতে পাওয়া যাবে।
অন্য কিছু উল্লেখ না করা থাকলে, এই পৃষ্ঠার কন্টেন্ট Creative Commons Attribution 4.0 License-এর অধীনে এবং কোডের নমুনাগুলি Apache 2.0 License-এর অধীনে লাইসেন্স প্রাপ্ত। আরও জানতে, Google Developers সাইট নীতি দেখুন। Java হল Oracle এবং/অথবা তার অ্যাফিলিয়েট সংস্থার রেজিস্টার্ড ট্রেডমার্ক।
2025-07-25 UTC-তে শেষবার আপডেট করা হয়েছে।
[null,null,["2025-07-25 UTC-তে শেষবার আপডেট করা হয়েছে।"],[],[],null,["# The Neural Structured Learning Framework\n\nNeural Structured Learning (NSL) focuses on training deep neural networks by\nleveraging structured signals (when available) along with feature inputs. As\nintroduced by [Bui et al. (WSDM'18)](https://research.google/pubs/pub46568.pdf),\nthese structured signals are used to regularize the training of a neural\nnetwork, forcing the model to learn accurate predictions (by minimizing\nsupervised loss), while at the same time maintaining the input structural\nsimilarity (by minimizing the neighbor loss, see the figure below). This\ntechnique is generic and can be applied on arbitrary neural architectures (such\nas Feed-forward NNs, Convolutional NNs and Recurrent NNs).\n\nNote that the generalized neighbor loss equation is flexible and can have other\nforms besides the one illustrated above. For example, we can also select\n\\\\(\\\\sum_{x_j \\\\in \\\\mathcal{N}(x_i)}\\\\mathcal{E}(y_i,g_\\\\theta(x_j))\\\\) to be the\nneighbor loss, which calculates the distance between the ground truth \\\\(y_i\\\\)\nand the prediction from the neighbor \\\\(g_\\\\theta(x_j)\\\\). This is commonly used in\nadversarial learning\n[(Goodfellow et al., ICLR'15)](https://arxiv.org/pdf/1412.6572.pdf). Therefore,\nNSL generalizes to **Neural Graph Learning** if neighbors are explicitly\nrepresented by a graph, and to **Adversarial Learning** if neighbors are\nimplicitly induced by adversarial perturbation.\n\nThe overall workflow for Neural Structured Learning is illustrated below. Black\narrows represent the conventional training workflow and red arrows represent the\nnew workflow as introduced by NSL to leverage structured signals. First, the\ntraining samples are augmented to include structured signals. When structured\nsignals are not explicitly provided, they can be either constructed or induced\n(the latter applies to adversarial learning). Next, the augmented training\nsamples (including both original samples and their corresponding neighbors) are\nfed to the neural network for calculating their embeddings. The distance between\na sample's embedding and its neighbor's embedding is calculated and used as the\nneighbor loss, which is treated as a regularization term and added to the final\nloss. For explicit neighbor-based regularization, we typically compute the\nneighbor loss as the distance between the sample's embedding and the neighbor's\nembedding. However, any layer of the neural network may be used to compute the\nneighbor loss. On the other hand, for induced neighbor-based regularization\n(adversarial), we compute the neighbor loss as the distance between the output\nprediction of the induced adversarial neighbor and the ground truth label.\n\nWhy use NSL?\n------------\n\nNSL brings the following advantages:\n\n- **Higher accuracy** : the structured signal(s) among samples can provide information that is not always available in feature inputs; therefore, the joint training approach (with both structured signals and features) has been shown to outperform many existing methods (that rely on training with features only) on a wide range of tasks, such as document classification and semantic intent classification ([Bui et al., WSDM'18](https://research.google/pubs/pub46568.pdf) \\& [Kipf et al., ICLR'17](https://arxiv.org/pdf/1609.02907.pdf)).\n- **Robustness** : models trained with adversarial examples have been shown to be robust against adversarial perturbations designed for misleading a model's prediction or classification ([Goodfellow et al., ICLR'15](https://arxiv.org/pdf/1412.6572.pdf) \\& [Miyato et al., ICLR'16](https://arxiv.org/pdf/1704.03976.pdf)). When the number of training samples is small, training with adversarial examples also helps improve model accuracy ([Tsipras et al., ICLR'19](https://arxiv.org/pdf/1805.12152.pdf)).\n- **Less labeled data required** : NSL enables neural networks to harness both labeled and unlabeled data, which extends the learning paradigm to [semi-supervised learning](https://en.wikipedia.org/wiki/Semi-supervised_learning). Specifically, NSL allows the network to train using labeled data as in the supervised setting, and at the same time drives the network to learn similar hidden representations for the \"neighboring samples\" that may or may not have labels. This technique has shown great promise for improving model accuracy when the amount of labeled data is relatively small ([Bui et al., WSDM'18](https://research.google/pubs/pub46568.pdf) \\& [Miyato et al., ICLR'16](https://arxiv.org/pdf/1704.03976.pdf)).\n\nStep-by-step Tutorials\n----------------------\n\nTo obtain hands-on experience with Neural Structured Learning, we have tutorials\nthat cover various scenarios where structured signals may be explicitly given,\nconstructed, or induced. Here are a few:\n\n- [Graph regularization for document classification using natural graphs](/neural_structured_learning/tutorials/graph_keras_mlp_cora).\n In this tutorial, we explore the use of graph regularization to classify\n documents that form a natural (organic) graph.\n\n- [Graph regularization for sentiment classification using synthesized graphs](/neural_structured_learning/tutorials/graph_keras_lstm_imdb).\n In this tutorial, we demonstrate the use of graph regularization to classify\n movie review sentiments by constructing (synthesizing) structured signals.\n\n- [Adversarial learning for image classification](/neural_structured_learning/tutorials/adversarial_keras_cnn_mnist).\n In this tutorial, we explore the use of adversarial learning (where\n structured signals are induced) to classify images containing numeric\n digits.\n\nMore examples and tutorials can be found in the\n[examples](https://github.com/tensorflow/neural-structured-learning/tree/master/neural_structured_learning/examples)\ndirectory of our GitHub repository."]]
