Pemrograman Probabilistik di Oryx

pip install -q -U jax jaxlib
pip install -q -Uq oryx -I
pip install -q tfp-nightly --upgrade

from functools import partial

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')

import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random

from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions

import oryx

Pemrograman probabilistik adalah gagasan bahwa kita dapat mengekspresikan model probabilistik menggunakan fitur dari bahasa pemrograman. Tugas seperti inferensi atau marginalisasi Bayesian kemudian disediakan sebagai fitur bahasa dan berpotensi dapat diotomatisasi.

Oryx menyediakan sistem pemrograman probabilistik di mana program probabilistik hanya dinyatakan sebagai fungsi Python; program-program ini kemudian ditransformasikan melalui transformasi fungsi yang dapat dikomposisi seperti yang ada di JAX! Idenya adalah untuk memulai dengan program sederhana (seperti pengambilan sampel dari normal acak) dan menyusunnya bersama untuk membentuk model (seperti jaringan saraf Bayesian). Poin penting dari desain PPL Oryx ini adalah untuk memungkinkan program untuk terlihat seperti fungsi kau sudah menulis dan digunakan dalam JAX, namun dijelaskan untuk membuat transformasi sadar mereka.

Mari impor dulu fungsionalitas inti PPL Oryx.

from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest

Apa program probabilistik di Oryx?

Di Oryx, program probabilistik hanyalah fungsi Python murni yang beroperasi pada nilai JAX dan kunci pseudorandom dan mengembalikan sampel acak. Dengan desain, mereka yang kompatibel dengan transformasi seperti jit dan vmap . Namun, Oryx sistem pemrograman probabilistik menyediakan alat yang memungkinkan Anda untuk membubuhi keterangan fungsi Anda dengan cara yang bermanfaat.

Mengikuti filosofi JAX fungsi murni, program probabilistik Oryx adalah fungsi Python yang mengambil JAX PRNGKey sebagai argumen pertama dan sejumlah argumen pendingin berikutnya. Output dari fungsi ini disebut "sampel" dan pembatasan yang sama yang berlaku untuk jit -ed dan vmap fungsi -ed berlaku untuk program probabilistik (misalnya tidak aliran data-dependent kontrol, tidak ada efek samping, dll). Ini berbeda dari banyak sistem pemrograman probabilistik imperatif di mana 'sampel' adalah seluruh jejak eksekusi, termasuk nilai-nilai internal untuk eksekusi program. Kita akan lihat nanti bagaimana Oryx dapat mengakses nilai-nilai internal yang menggunakan joint_sample , dibahas di bawah.

Program :: PRNGKey -> ... -> Sample

Berikut ini adalah "hello world" program yang sampel dari distribusi log-normal .

def log_normal(key):
  return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))

print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
0.8139614
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

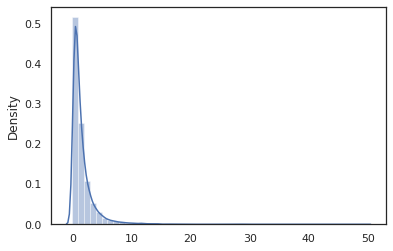
The log_normal fungsi pembungkus tipis sekitar Tensorflow Probability (TFP) distribusi, tapi bukannya memanggil tfd.Normal(0., 1.).sample , kami telah digunakan random_variable sebagai gantinya. Seperti yang akan kita lihat nanti, random_variable memungkinkan kita untuk mengkonversi objek ke dalam program probabilistik, bersama dengan fungsi yang berguna lainnya.

Kita dapat mengkonversi log_normal menjadi fungsi log-density menggunakan log_prob transformasi:

print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()

-0.9189385

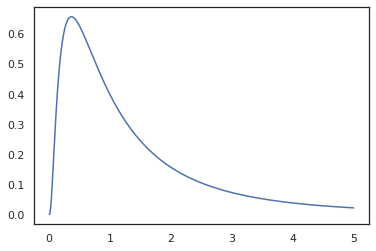
Karena kita sudah dijelaskan fungsi dengan random_variable , log_prob menyadari bahwa ada panggilan untuk tfd.Normal(0., 1.).sample dan menggunakan tfd.Normal(0., 1.).log_prob untuk menghitung distribusi dasar masalah log. Untuk menangani jnp.exp , ppl.log_prob otomatis menghitung kepadatan melalui fungsi bijektif, melacak perubahan volume dalam perubahan-of-variabel perhitungan.

Di Oryx, kita dapat mengambil program dan mengubah mereka menggunakan transformasi fungsi - misalnya, jax.jit atau log_prob . Oryx tidak dapat melakukan ini dengan sembarang program; itu membutuhkan fungsi pengambilan sampel yang telah mendaftarkan fungsi kepadatan lognya dengan Oryx. Untungnya, Oryx otomatis register Probabilitas TensorFlow (TFP) distribusi dalam sistem.

Alat pemrograman probabilistik Oryx

Oryx memiliki beberapa transformasi fungsi yang diarahkan pada pemrograman probabilistik. Kami akan membahas sebagian besar dari mereka dan memberikan beberapa contoh. Pada akhirnya, kami akan menggabungkan semuanya menjadi studi kasus MCMC. Anda juga dapat mengacu pada dokumentasi untuk core.ppl.transformations untuk lebih jelasnya.

random_variable

random_variable memiliki dua bagian utama dari fungsi, baik difokuskan pada annotating fungsi Python dengan informasi yang dapat digunakan dalam transformasi.

1. random_variable 'beroperasi sebagai fungsi identitas secara default, tetapi dapat menggunakan pendaftaran tipe-spesifik untuk benda mengkonversi ke programs.` probabilistik

   Untuk jenis callable (fungsi Python, lambdas, functools.partial s, dll) dan sewenang-wenang object s (seperti JAX DeviceArray s) itu hanya akan kembali input.

   random_variable(x: object) == x
   random_variable(f: Callable[...]) == f
   

   Oryx otomatis register TensorFlow Probability (TFP) distribusi, yang diubah menjadi program probabilistik yang menyebut distribusi ini sample metode.

   random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235
   

   Oryx juga menyematkan informasi tentang distribusi TFP ke dalam jejak JAX yang memungkinkan penghitungan kepadatan log secara otomatis.

2. random_variable nilai kaleng tag dengan nama, membuat mereka berguna untuk transformasi hilir, dengan menyediakan opsional name kata kunci argumen untuk random_variable . Ketika kami melewati sebuah array ke dalam random_variable bersama dengan name (misalnya random_variable(x, name='x') ), itu hanya tag nilai dan kembali itu. Jika kita lulus dalam callable atau distribusi TFP, random_variable kembali program yang tag sampel output dengan name .

Penjelasan ini tidak mengubah semantik program ketika dijalankan, tetapi hanya jika berubah (yaitu program akan mengembalikan nilai yang sama dengan atau tanpa menggunakan random_variable ).

Mari kita lihat contoh di mana kita menggunakan kedua bagian fungsi bersama-sama.

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

Dalam program ini kami telah menandai intermediet z dan x , yang membuat transformasi joint_sample , intervene , conditional dan graph_replace menyadari nama 'z' dan 'x' . Kami akan membahas dengan tepat bagaimana setiap transformasi menggunakan nama nanti.

log_prob

The log_prob fungsi transformasi mengkonversi program probabilistik Oryx ke dalam fungsi log-density-nya. Fungsi densitas log ini mengambil sampel potensial dari program sebagai input dan mengembalikan densitas lognya di bawah distribusi sampling yang mendasarinya.

log_prob :: Program -> (Sample -> LogDensity)

Seperti random_variable , ia bekerja melalui registry jenis mana distribusi TFP secara otomatis terdaftar, sehingga log_prob(tfd.Normal(0., 1.)) panggilan tfd.Normal(0., 1.).log_prob . Untuk fungsi Python, bagaimanapun, log_prob menelusuri program menggunakan JAX dan terlihat untuk sampling pernyataan. The log_prob transformasi bekerja pada sebagian besar program yang kembali variabel acak, secara langsung atau melalui transformasi dibalik tapi tidak pada program yang nilai-nilai sampel internal yang tidak dikembalikan. Jika tidak dapat membalikkan operasi yang diperlukan dalam program ini, log_prob akan melemparkan kesalahan.

Berikut adalah beberapa contoh log_prob diterapkan untuk berbagai program.

1. log_prob bekerja pada program-program yang langsung sampel dari distribusi TFP (atau jenis lain yang terdaftar) dan kembali nilai-nilai mereka.

def normal(key):
  return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))

-0.9189385

1. log_prob mampu menghitung log-kepadatan sampel dari program yang mengubah variates acak menggunakan fungsi bijektif (misalnya jnp.exp , jnp.tanh , jnp.split ).

def log_normal(key):
  return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))

-1.159165

Dalam rangka untuk menghitung sampel dari log_normal 's log-density, kita harus terlebih dahulu membalikkan exp , mengambil log sampel, dan kemudian menambahkan koreksi volume perubahan menggunakan log-det terbalik Jacobian dari exp (lihat perubahan variabel formula dari Wikipedia).

1. log_prob bekerja dengan program yang struktur output sampel suka, kamus Python atau tupel.

def normal_2d(key):
  x = random_variable(
    tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
  x1, x2 = jnp.split(x, 2, 0)
  return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))

{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546

1. log_prob berjalan grafik perhitungan ditelusuri dari fungsi, komputasi kedua nilai maju dan terbalik (dan log-det mereka Jacobian) bila diperlukan dalam upaya untuk menghubungkan nilai-nilai kembali dengan dasar nilai-nilai mereka sampel melalui perubahan yang didefinisikan dengan variabel. Ambil contoh program berikut:

def complex_program(key):
  k1, k2 = random.split(key)
  z = random_variable(tfd.Normal(0., 1.))(k1)
  x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
  return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))

(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32))
-1.0967848

Dalam program ini, kami sampel x bersyarat pada z , berarti kita perlu nilai z sebelum kita dapat menghitung log-kepadatan x . Namun, dalam rangka untuk menghitung z , pertama kita harus membalikkan jnp.exp diterapkan z . Dengan demikian, dalam rangka untuk menghitung log-kepadatan dari x dan z , log_prob kebutuhan untuk pertama invert keluaran pertama, dan kemudian menyebarkannya ke depan melalui jax.nn.relu untuk menghitung rata-rata p(x | z) .

Catatan: sementara log_prob tidak akan bekerja pada program-program yang variabel acak sampel yang tidak dikembalikan sebagai output, joint_sample dapat mengkonversi program ke satu yang tidak.

Untuk informasi lebih lanjut tentang log_prob , Anda dapat merujuk ke core.interpreters.log_prob . Dalam pelaksanaannya, log_prob erat didasarkan dari inverse transformasi JAX; untuk mempelajari lebih lanjut tentang inverse , lihat core.interpreters.inverse .

joint_sample

Untuk mendefinisikan program yang lebih kompleks dan menarik, kita akan menggunakan beberapa variabel acak laten, yaitu variabel acak dengan nilai yang tidak teramati. Mari kita mengacu pada latent_normal program yang sampel nilai acak z yang digunakan sebagai mean lain nilai acak x .

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

Dalam program ini, z begitu laten jika kita hanya memanggil latent_normal(random.PRNGKey(0)) kita tidak akan tahu nilai sebenarnya dari z yang bertanggung jawab untuk menghasilkan x .

joint_sample adalah transformasi yang transformasi program ke program lain yang kembali kamus pemetaan nama string yang (tag) untuk nilai-nilai mereka. Agar berfungsi, kita perlu memastikan bahwa kita memberi tag pada variabel laten untuk memastikan variabel tersebut muncul dalam output fungsi yang diubah.

joint_sample(latent_normal)(random.PRNGKey(0))

{'x': DeviceArray(0.01873656, dtype=float32),
 'z': DeviceArray(0.14389044, dtype=float32)}

Perhatikan bahwa joint_sample transformasi program ke program lain yang sampel distribusi bersama atas nilai-nilai laten, sehingga kita dapat lebih mengubahnya. Untuk algoritme seperti MCMC dan VI, biasanya menghitung probabilitas log dari distribusi gabungan sebagai bagian dari prosedur inferensi. log_prob(latent_normal) tidak bekerja karena memerlukan meminggirkan keluar z , tapi kita bisa menggunakan log_prob(joint_sample(latent_normal)) .

print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))

-50.03529
-5049.535

Karena ini adalah suatu pola umum, Oryx juga memiliki joint_log_prob transformasi yang hanya komposisi log_prob dan joint_sample .

print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))

-50.03529
-5049.535

block

The block transformasi mengambil dalam program dan urutan nama dan mengembalikan program yang berperilaku identik kecuali bahwa dalam transformasi hilir (seperti joint_sample ), nama-nama yang disediakan diabaikan. Contoh di mana block berguna mengkonversi distribusi bersama menjadi sebelum selama variabel laten dengan "memblokir" nilai-nilai sampel di kemungkinan. Sebagai contoh, mengambil latent_normal , yang pertama kali menggambar z ~ N(0, 1) maka x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) adalah sebuah program yang menyembunyikan para x nama, jadi jika kita melakukan joint_sample(block(latent_normal, names=['x'])) , kita memperoleh sebuah kamus hanya dengan z di dalamnya .

blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))

{'z': DeviceArray(0.14389044, dtype=float32)}

intervene

The intervene clobbers transformasi sampel dalam program probabilistik dengan nilai-nilai dari luar. Akan kembali ke kami latent_normal Program, katakanlah kami tertarik dalam menjalankan program yang sama tetapi ingin z harus diperbaiki untuk 4. Daripada menulis program baru, kita dapat menggunakan intervene untuk mengesampingkan nilai z .

intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();

/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

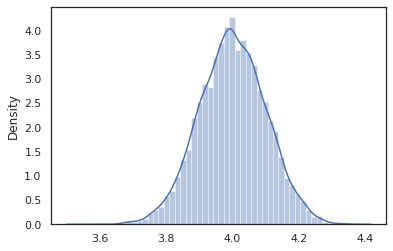
The intervened sampel fungsi dari p(x | do(z = 4)) yang hanya distribusi normal standar berpusat di 4. Ketika kita intervene pada nilai tertentu, nilai yang tidak lagi dianggap sebagai variabel acak. Ini berarti bahwa z nilai tidak akan ditandai ketika menjalankan intervened .

conditional

conditional transformasi program yang sampel laten nilai-nilai ke dalam satu kondisi pada nilai-nilai laten. Kembali ke kami latent_normal program, yang sampel p(x) dengan laten z , kita bisa mengubahnya menjadi sebuah program bersyarat p(x | z) .

cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()

99.87485
49.874847
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

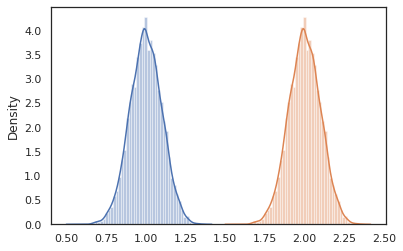
nest

Ketika kita mulai menyusun program probabilistik untuk membangun yang lebih kompleks, biasanya kita menggunakan kembali fungsi yang memiliki beberapa logika penting. Sebagai contoh, jika kita ingin membangun jaringan saraf Bayesian, mungkin ada yang penting dense program yang sampel bobot dan mengeksekusi maju lulus.

Jika kita menggunakan kembali fungsi, namun, kami mungkin berakhir dengan nilai-nilai tag duplikat dalam program akhir, yang dianulir oleh transformasi seperti joint_sample . Kita dapat menggunakan nest untuk membuat tag "scopes" di mana setiap sampel dalam lingkup bernama akan dimasukkan ke kamus bersarang.

def f(key):
  return random_variable(tfd.Normal(0., 1.), name='x')(key)

def g(key):
  k1, k2 = random.split(key)
  return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))

{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
 'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }

Studi kasus: Jaringan saraf Bayesian

Mari kita mencoba tangan kami di pelatihan jaringan saraf Bayesian untuk mengklasifikasikan klasik Fisher Iris dataset. Ini relatif kecil dan berdimensi rendah sehingga kami dapat mencoba langsung mengambil sampel posterior dengan MCMC.

Pertama, mari impor dataset dan beberapa utilitas tambahan dari Oryx.

from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']

num_features = features.shape[-1]
num_classes = len(iris.target_names)

from oryx.experimental import mcmc
from oryx.util import summary, get_summaries

Kita mulai dengan menerapkan lapisan padat, yang akan memiliki prioritas normal di atas bobot dan bias. Untuk melakukan ini, pertama kita mendefinisikan dense fungsi yang lebih tinggi yang mengambil output dimensi dan aktivasi fungsi yang diinginkan. The dense mengembalikan fungsi program probabilistik yang mewakili distribusi bersyarat p(h | x) di mana h adalah output dari lapisan padat dan x adalah input. Ini sampel pertama berat dan bias dan kemudian berlaku mereka untuk x .

def dense(dim_out, activation=jax.nn.relu):
  def forward(key, x):
    dim_in = x.shape[-1]
    w_key, b_key = random.split(key)
    w = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
          name='w')(w_key)
    b = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
          name='b')(b_key)
    return activation(jnp.dot(w, x) + b)
  return forward

Untuk menulis beberapa dense lapisan bersama-sama, kami akan menerapkan mlp (multilayer perceptron) fungsi yang lebih tinggi yang diperlukan dalam daftar ukuran tersembunyi dan sejumlah kelas. Ia mengembalikan program yang berulang kali memanggil dense menggunakan sesuai hidden_size dan akhirnya kembali logits untuk setiap kelas di lapisan akhir. Perhatikan penggunaan nest yang menciptakan nama lingkup untuk setiap lapisan.

def mlp(hidden_sizes, num_classes):
  num_hidden = len(hidden_sizes)
  def forward(key, x):
    keys = random.split(key, num_hidden + 1)
    for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
      x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
    logits = nest(dense(num_classes, activation=lambda x: x),
                  scope=f'layer_{num_hidden + 1}')(keys[-1], x)
    return logits
  return forward

Untuk mengimplementasikan model lengkap, kita perlu memodelkan label sebagai variabel acak kategoris. Kami akan menentukan predict fungsi yang mengambil dalam dataset dari xs (fitur) yang kemudian diteruskan ke dalam mlp menggunakan vmap . Ketika kita menggunakan vmap(partial(mlp, mlp_key)) , kami mencicipi satu set bobot, tetapi memetakan maju lulus atas semua masukan xs . Ini menghasilkan satu set logits yang parameterizes distribusi kategoris independen.

def predict(mlp):
  def forward(key, xs):
    mlp_key, label_key = random.split(key)
    logits = vmap(partial(mlp, mlp_key))(xs)
    return random_variable(
        tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
  return forward

Itu model lengkapnya! Mari kita gunakan MCMC untuk sampel posterior dari bobot BNN data yang diberikan; pertama kita membangun BNN "template" menggunakan mlp .

bnn = mlp([200, 200], num_classes)

Untuk membangun sebuah titik awal untuk rantai Markov kami, kita dapat menggunakan joint_sample dengan masukan dummy.

weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())

dict_keys(['layer_1', 'layer_2', 'layer_3'])

Menghitung probabilitas log distribusi gabungan sudah cukup untuk banyak algoritma inferensi. Mari kita sekarang mengatakan kita amati x dan ingin sampel posterior p(z | x) . Untuk distribusi yang kompleks, kita tidak akan bisa meminggirkan keluar x (meskipun untuk latent_normal kita bisa) tapi kita bisa menghitung sebuah unnormalized density log log p(z, x) di mana x adalah tetap untuk nilai tertentu. Kita dapat menggunakan probabilitas log yang tidak dinormalisasi dengan MCMC untuk mengambil sampel posterior. Mari kita tulis fungsi log prob "disematkan" ini.

def target_log_prob(weights):
  return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)

Sekarang kita dapat menggunakan tfp.mcmc untuk sampel posterior menggunakan fungsi kepadatan log unnormalized kami. Perhatikan bahwa kita harus menggunakan "rata" versi bobot bersarang kami kamus agar kompatibel dengan tfp.mcmc , jadi kami menggunakan utilitas pohon JAX untuk meratakan dan unflatten.

@jit
def run_chain(key, weights):
  flat_state, sample_tree = jax.tree_flatten(weights)

  def flat_log_prob(*states):
    return target_log_prob(jax.tree_unflatten(sample_tree, states))

  def trace_fn(_, results):
    return results.inner_results.accepted_results.target_log_prob

  flat_states, log_probs = tfp.mcmc.sample_chain(
    1000,
    num_burnin_steps=9000,
    kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
        tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
        9000, target_accept_prob=0.7),
    trace_fn=trace_fn,
    current_state=flat_state,
    seed=key)
  samples = jax.tree_unflatten(sample_tree, flat_states)
  return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)

plt.plot(log_probs)
plt.show()

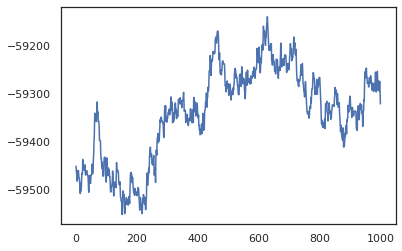
Kami dapat menggunakan sampel kami untuk mengambil perkiraan rata-rata model Bayesian (BMA) dari akurasi pelatihan. Untuk menghitung itu, kita dapat menggunakan intervene dengan bnn untuk "menyuntikkan" posterior bobot di tempat orang-orang yang sampel dari kunci. Untuk menghitung logits untuk setiap titik data untuk setiap sampel posterior, kita dapat melipatgandakan vmap lebih posterior_weights dan features .

output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
    random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)

print('Average sample accuracy:', (
    output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
    output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())

Average sample accuracy: 0.9874067
BMA accuracy: 0.99333334

Kesimpulan

Di Oryx, program probabilistik hanyalah fungsi JAX yang menerima (pseudo-)randomness sebagai input. Karena integrasi erat Oryx dengan sistem transformasi fungsi JAX, kita dapat menulis dan memanipulasi program probabilistik seperti kita sedang menulis kode JAX. Ini menghasilkan sistem yang sederhana namun fleksibel untuk membangun model yang kompleks dan melakukan inferensi.