Введение в сети RL и Deep Q

Посмотреть на TensorFlow.org Запускаем в Google Colab Посмотреть исходный код на GitHub Скачать блокнот

Вступление

Обучение с подкреплением (RL) - это общая структура, в которой агенты учатся выполнять действия в среде, чтобы получить максимальное вознаграждение. Двумя основными компонентами являются среда, которая представляет проблему, которую необходимо решить, и агент, который представляет алгоритм обучения.

Агент и среда постоянно взаимодействуют друг с другом. На каждом временном шаге, агент принимает действие на окружающей среду на основе его политика \(\pi(a_t|s_t)\), где \(s_t\) является текущим наблюдением из окружающей среды, и получает вознаграждение \(r_{t+1}\) и следующее наблюдение , \(s_{t+1}\) из окружающей среды . Цель состоит в том, чтобы улучшить политику, чтобы максимизировать сумму вознаграждений (возврат).

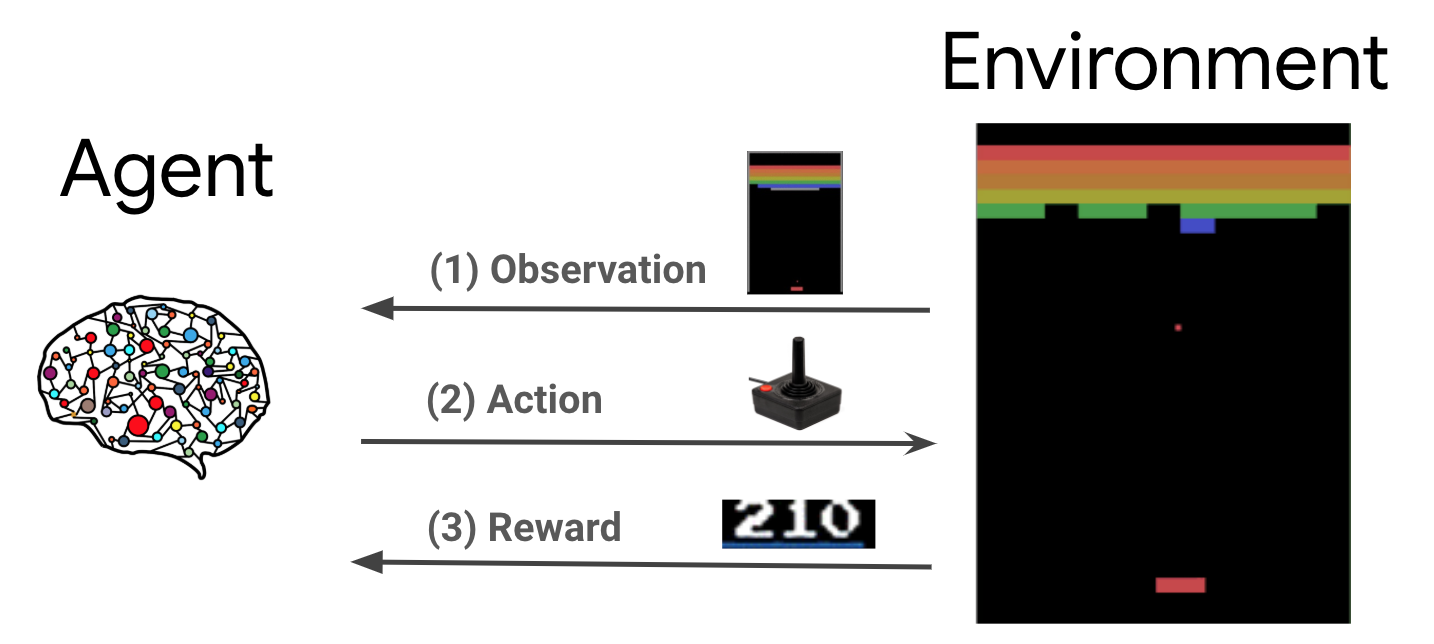
Цикл взаимодействия агента и среды

Это очень общая структура, которая может моделировать различные последовательные задачи принятия решений, такие как игры, робототехника и т. Д.

Окружающая среда Cartpole

Среда Cartpole является одним из самых известных классических проблем обучения с подкреплением (далее «Hello, World!» ЛР). К тележке прикреплен шест, который может двигаться по бесфрикционной дорожке. Столб начинается вертикально, и цель состоит в том, чтобы не допустить его падения, управляя тележкой.

  • Наблюдения из окружающей среды \(s_t\) представляет собой вектор , представляющий 4D положение и скорость тележки, а также угол и угловую скорость полюса.
  • Агент может управлять системой, принимая один из 2 -х действиях \(a_t\): толкать тележки право (+1) или влево (-1).
  • Вознаграждение \(r_{t+1} = 1\) предоставляется для каждого временного шага , что полюс остается в вертикальном положении. Эпизод заканчивается, когда выполняется одно из следующих условий:
    • полюс превышает некоторый предел угла
    • тележка движется за пределы краев мира
    • Проходит 200 временных шагов.

Цель агента является изучение политики \(\pi(a_t|s_t)\) так, чтобы максимизировать сумму вознаграждения в эпизоде \(\sum_{t=0}^{T} \gamma^t r_t\). Здесь \(\gamma\) является коэффициент дисконтирования в \([0, 1]\) , что скидки в будущем награды относительно немедленного вознаграждения. Этот параметр помогает нам сфокусировать политику, заставляя ее больше заботиться о быстром получении вознаграждений.

Агент DQN

Алгоритм DQN (Deep Q-Network) была разработана DeepMind в 2015 году удалось решить широкий спектр Атари игр (некоторые сверхчеловеческого уровня) путем объединения обучения с подкреплением и глубокие нейронные сети в масштабе. Алгоритм был разработан за счетом повышения классического алгоритма RL под названием Q-Learning с глубокими нейронными сетями и методом , называемым опытом повторе.

Q-Learning

Q-Learning основано на понятии Q-функции. Q-функция (ака значение функции состояния действия) политики \(\pi\), \(Q^{\pi}(s, a)\), меры ожидаемой доходности или дисконтированной суммы вознаграждений , полученных из государственного \(s\) путем принятия мер \(a\) первой и после политики \(\pi\) после этого. Определим оптимальную Q-функцию \(Q^*(s, a)\) как максимальную отдачу , которую можно получить , исходя из наблюдений \(s\), принимая действие \(a\) и следуя политике оптимальной в дальнейшем. Q-функция оптимальной подчиняется следующему уравнению Беллмана оптимальности:

\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)

Это означает , что максимальная отдача от состояния \(s\) и действия \(a\) является суммой немедленного вознаграждения \(r\) и возвращение (льгота \(\gamma\)) , полученное не следуя политику оптимальной после этого до конца эпизода ( то есть, максимальное вознаграждение от следующего состояния \(s'\)). Ожидание вычисляется как по распределению непосредственных выгод \(r\) и возможных следующих состояний \(s'\).

Основная идея Q-Learning является использование Беллмана уравнения оптимальности как итеративное обновление \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\), и можно показать , что это сходится к оптимальному \(Q\)-функции, т.е. \(Q_i \rightarrow Q^*\) , как \(i \rightarrow \infty\) (см DQN бумага ).

Глубокое Q-обучение

Для большинства проблем, это нецелесообразно , чтобы представить \(Q\)-функции в виде таблицы , содержащей значения для каждой комбинации \(s\) и \(a\). Вместо этого, мы обучаем функцию аппроксиматором, например нейронной сети с параметрами \(\theta\), для оценки Q-значений, т.е. \(Q(s, a; \theta) \approx Q^*(s, a)\). Это можно сделать путем минимизации следующей потери на каждом шаге \(i\):

\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) где \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)

Здесь \(y_i\) называется целевым TD (временная разница) и \(y_i - Q\) называется ошибка TD. \(\rho\) представляет собой распределение поведения, распределение по переходам \(\{s, a, r, s'\}\) , собранных из окружающей среды.

Обратите внимание , что параметры из предыдущей итерации \(\theta_{i-1}\) являются фиксированными и не обновляются. На практике мы используем снимок параметров сети с нескольких итераций назад вместо последней итерации. Эта копия называется целевой сетью.

Q-Learning является алгоритмом вне политики , которая узнает о жадных политиках \(a = \max_{a} Q(s, a; \theta)\) , используя другую политику поведения для действующих в окружающей среде / сборе данных. Эта политика поведения, как правило, \(\epsilon\)-greedy политик , которая выбирает жадное действие с вероятностью \(1-\epsilon\) и случайным действием с вероятностью \(\epsilon\) , чтобы обеспечить хорошее покрытие пространства государства действий.

Опыт Replay

Чтобы избежать вычисления полного ожидания потери DQN, мы можем минимизировать его, используя стохастический градиентный спуск. Если потери вычисляется с использованием только последней перехода \(\{s, a, r, s'\}\), это сводится к стандартному Q-Learning.

Работа Atari DQN представила технику под названием Experience Replay, чтобы сделать обновления сети более стабильными. На каждом временном шаге сбора данных, переходы добавляются в кольцевой буфер называется повтор буфер. Затем во время обучения, вместо того, чтобы использовать только последний переход для вычисления потерь и его градиента, мы вычисляем их, используя мини-пакет переходов, выбранных из буфера воспроизведения. Это дает два преимущества: лучшая эффективность данных за счет повторного использования каждого перехода во многих обновлениях и лучшая стабильность за счет использования некоррелированных переходов в пакете.

DQN на Cartpole в TF-Agents

TF-Agents предоставляет все компоненты, необходимые для обучения агента DQN, такие как сам агент, среда, политики, сети, буферы воспроизведения, циклы сбора данных и показатели. Эти компоненты реализованы как функции Python или графические операции TensorFlow, и у нас также есть оболочки для преобразования между ними. Кроме того, TF-Agents поддерживает режим TensorFlow 2.0, который позволяет нам использовать TF в императивном режиме.

Далее, посмотрите на учебник для обучения DQN агента на окружающую среду Cartpole с использованием TF-агентов .