Эта страница переведена с помощью Cloud Translation API.

Дифференциальная конфиденциальность в TFF

Посмотреть на TensorFlow.org

Запускаем в Google Colab

Посмотреть исходный код на GitHub

Скачать блокнот

В этом руководстве будут продемонстрированы рекомендуемые лучшие практики для обучения моделей с дифференциальной конфиденциальностью на уровне пользователя с использованием Tensorflow Federated. Мы будем использовать алгоритм DP-SGD из Абади и др., «Глубокое изучение с дифференциальной конфиденциальностью» модифицированном для пользовательского уровня DP в федеративной контексте в McMahan и др., «Изучение Дифференциальна частный Рецидив языке Models» .

Дифференциальная конфиденциальность (DP) - это широко используемый метод ограничения и количественной оценки утечки конфиденциальных данных при выполнении учебных задач. Обучение модели с DP на уровне пользователя гарантирует, что модель вряд ли узнает что-либо существенное о данных любого человека, но все же может (надеюсь!) Изучить шаблоны, которые существуют в данных многих клиентов.

Мы обучим модель на федеративном наборе данных EMNIST. Существует неизбежный компромисс между полезностью и конфиденциальностью, и может быть трудно обучить модель с высокой степенью конфиденциальности, которая будет работать так же, как современная непубличная модель. Для удобства в этом руководстве мы будем тренироваться всего за 100 раундов, жертвуя некоторым качеством, чтобы продемонстрировать, как тренироваться с высокой конфиденциальностью. Если бы мы использовали больше обучающих раундов, мы, безусловно, могли бы получить частную модель с несколько более высокой точностью, но не такой высокой, как модель, обученная без DP.

Прежде чем мы начнем

Во-первых, давайте убедимся, что ноутбук подключен к бэкэнду, на котором скомпилированы соответствующие компоненты.

!pip install --quiet --upgrade tensorflow_federated_nightly
!pip install --quiet --upgrade nest-asyncio

import nest_asyncio
nest_asyncio.apply()

Некоторый импорт нам понадобится для учебника. Мы будем использовать tensorflow_federated , рамки с открытым исходным кодом для машинного обучения и других вычислений на децентрализованных данных, а также tensorflow_privacy , библиотека с открытым исходным кодом для осуществления и анализа дифференцированно частных алгоритмов tensorflow.

import collections

import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_federated as tff
import tensorflow_privacy as tfp

Выполните следующий пример «Hello World», чтобы убедиться, что среда TFF настроена правильно. Если он не работает, пожалуйста , обратитесь к установке руководству для получения инструкций.

@tff.federated_computation
def hello_world():
  return 'Hello, World!'

hello_world()

b'Hello, World!'

Загрузите и предварительно обработайте объединенный набор данных EMNIST.

def get_emnist_dataset():
  emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data(
      only_digits=True)

  def element_fn(element):
    return collections.OrderedDict(
        x=tf.expand_dims(element['pixels'], -1), y=element['label'])

  def preprocess_train_dataset(dataset):
    # Use buffer_size same as the maximum client dataset size,
    # 418 for Federated EMNIST
    return (dataset.map(element_fn)
                   .shuffle(buffer_size=418)
                   .repeat(1)
                   .batch(32, drop_remainder=False))

  def preprocess_test_dataset(dataset):
    return dataset.map(element_fn).batch(128, drop_remainder=False)

  emnist_train = emnist_train.preprocess(preprocess_train_dataset)
  emnist_test = preprocess_test_dataset(
      emnist_test.create_tf_dataset_from_all_clients())
  return emnist_train, emnist_test

train_data, test_data = get_emnist_dataset()

Определите нашу модель.

def my_model_fn():
  model = tf.keras.models.Sequential([
      tf.keras.layers.Reshape(input_shape=(28, 28, 1), target_shape=(28 * 28,)),
      tf.keras.layers.Dense(200, activation=tf.nn.relu),
      tf.keras.layers.Dense(200, activation=tf.nn.relu),
      tf.keras.layers.Dense(10)])
  return tff.learning.from_keras_model(
      keras_model=model,
      loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
      input_spec=test_data.element_spec,
      metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])

Определите шумовую чувствительность модели.

Чтобы получить гарантии DP на уровне пользователя, мы должны изменить базовый алгоритм федеративного усреднения двумя способами. Во-первых, обновления модели клиентов должны быть обрезаны перед передачей на сервер, что ограничивает максимальное влияние любого клиента. Во-вторых, сервер должен добавить достаточно шума к сумме пользовательских обновлений перед усреднением, чтобы скрыть влияние клиента в худшем случае.

Для вырезки, мы используем метод адаптивного отсечения Эндрю и др. 2021, Дифференциально Частное обучение с адаптивным Clipping , так что не вырезка норма не должна быть явно установлена.

Добавление шума в целом ухудшает полезность модели, но мы можем контролировать количество шума в среднем обновлении на каждом этапе с помощью двух регуляторов: стандартное отклонение гауссовского шума, добавляемого к сумме, и количество клиентов в средний. Наша стратегия будет заключаться в том, чтобы сначала определить, сколько шума модель может выдержать при относительно небольшом количестве клиентов за цикл с приемлемыми потерями для полезности модели. Затем, чтобы обучить окончательную модель, мы можем увеличить количество шума в сумме, пропорционально увеличивая количество клиентов за раунд (при условии, что набор данных достаточно велик, чтобы поддерживать такое количество клиентов за раунд). Маловероятно, что это существенно повлияет на качество модели, поскольку единственный эффект - уменьшить дисперсию из-за выборки клиентов (действительно, мы проверим, что в нашем случае это не так).

С этой целью мы сначала обучаем серию моделей с 50 клиентами за раунд, с возрастающим уровнем шума. В частности, мы увеличиваем «noise_multiplier», которая представляет собой отношение стандартного отклонения шума к норме ограничения. Поскольку мы используем адаптивное отсечение, это означает, что реальная величина шума меняется от округления к округлению.

# Run five clients per thread. Increase this if your runtime is running out of
# memory. Decrease it if you have the resources and want to speed up execution.
tff.backends.native.set_local_python_execution_context(clients_per_thread=5)

total_clients = len(train_data.client_ids)

def train(rounds, noise_multiplier, clients_per_round, data_frame):
  # Using the `dp_aggregator` here turns on differential privacy with adaptive
  # clipping.
  aggregation_factory = tff.learning.model_update_aggregator.dp_aggregator(
      noise_multiplier, clients_per_round)

  # We use Poisson subsampling which gives slightly tighter privacy guarantees
  # compared to having a fixed number of clients per round. The actual number of
  # clients per round is stochastic with mean clients_per_round.
  sampling_prob = clients_per_round / total_clients

  # Build a federated averaging process.
  # Typically a non-adaptive server optimizer is used because the noise in the
  # updates can cause the second moment accumulators to become very large
  # prematurely.
  learning_process = tff.learning.build_federated_averaging_process(
        my_model_fn,
        client_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.01),
        server_optimizer_fn=lambda: tf.keras.optimizers.SGD(1.0, momentum=0.9),
        model_update_aggregation_factory=aggregation_factory)

  eval_process = tff.learning.build_federated_evaluation(my_model_fn)

  # Training loop.
  state = learning_process.initialize()
  for round in range(rounds):
    if round % 5 == 0:
      metrics = eval_process(state.model, [test_data])['eval']
      if round < 25 or round % 25 == 0:
        print(f'Round {round:3d}: {metrics}')
      data_frame = data_frame.append({'Round': round,
                                      'NoiseMultiplier': noise_multiplier,
                                      **metrics}, ignore_index=True)

    # Sample clients for a round. Note that if your dataset is large and
    # sampling_prob is small, it would be faster to use gap sampling.
    x = np.random.uniform(size=total_clients)
    sampled_clients = [
        train_data.client_ids[i] for i in range(total_clients)
        if x[i] < sampling_prob]
    sampled_train_data = [
        train_data.create_tf_dataset_for_client(client)
        for client in sampled_clients]

    # Use selected clients for update.
    state, metrics = learning_process.next(state, sampled_train_data)

  metrics = eval_process(state.model, [test_data])['eval']
  print(f'Round {rounds:3d}: {metrics}')
  data_frame = data_frame.append({'Round': rounds,
                                  'NoiseMultiplier': noise_multiplier,
                                  **metrics}, ignore_index=True)

  return data_frame

data_frame = pd.DataFrame()
rounds = 100
clients_per_round = 50

for noise_multiplier in [0.0, 0.5, 0.75, 1.0]:
  print(f'Starting training with noise multiplier: {noise_multiplier}')
  data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
  print()

Starting training with noise multiplier: 0.0
Round   0: OrderedDict([('sparse_categorical_accuracy', 0.112289384), ('loss', 2.5190482)])
Round   5: OrderedDict([('sparse_categorical_accuracy', 0.19075724), ('loss', 2.2449977)])
Round  10: OrderedDict([('sparse_categorical_accuracy', 0.18115693), ('loss', 2.163907)])
Round  15: OrderedDict([('sparse_categorical_accuracy', 0.49970612), ('loss', 2.01017)])
Round  20: OrderedDict([('sparse_categorical_accuracy', 0.5333317), ('loss', 1.8350543)])
Round  25: OrderedDict([('sparse_categorical_accuracy', 0.5828517), ('loss', 1.6551636)])
Round  50: OrderedDict([('sparse_categorical_accuracy', 0.7352077), ('loss', 0.8700141)])
Round  75: OrderedDict([('sparse_categorical_accuracy', 0.7769152), ('loss', 0.6992781)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.8049814), ('loss', 0.62453026)])

Starting training with noise multiplier: 0.5
Round   0: OrderedDict([('sparse_categorical_accuracy', 0.09526841), ('loss', 2.4332638)])
Round   5: OrderedDict([('sparse_categorical_accuracy', 0.20128821), ('loss', 2.2664592)])
Round  10: OrderedDict([('sparse_categorical_accuracy', 0.35472178), ('loss', 2.130336)])
Round  15: OrderedDict([('sparse_categorical_accuracy', 0.5480995), ('loss', 1.9713942)])
Round  20: OrderedDict([('sparse_categorical_accuracy', 0.42246276), ('loss', 1.8045483)])
Round  25: OrderedDict([('sparse_categorical_accuracy', 0.624902), ('loss', 1.4785467)])
Round  50: OrderedDict([('sparse_categorical_accuracy', 0.7265625), ('loss', 0.85801566)])
Round  75: OrderedDict([('sparse_categorical_accuracy', 0.77720904), ('loss', 0.70615387)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7702537), ('loss', 0.72331005)])

Starting training with noise multiplier: 0.75
Round   0: OrderedDict([('sparse_categorical_accuracy', 0.098672606), ('loss', 2.422002)])
Round   5: OrderedDict([('sparse_categorical_accuracy', 0.11794671), ('loss', 2.2227976)])
Round  10: OrderedDict([('sparse_categorical_accuracy', 0.3208513), ('loss', 2.083766)])
Round  15: OrderedDict([('sparse_categorical_accuracy', 0.49752644), ('loss', 1.8728142)])
Round  20: OrderedDict([('sparse_categorical_accuracy', 0.5816761), ('loss', 1.6084186)])
Round  25: OrderedDict([('sparse_categorical_accuracy', 0.62896746), ('loss', 1.378527)])
Round  50: OrderedDict([('sparse_categorical_accuracy', 0.73153406), ('loss', 0.8705139)])
Round  75: OrderedDict([('sparse_categorical_accuracy', 0.7789724), ('loss', 0.7113147)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.70944357), ('loss', 0.89495045)])

Starting training with noise multiplier: 1.0
Round   0: OrderedDict([('sparse_categorical_accuracy', 0.12002841), ('loss', 2.60482)])
Round   5: OrderedDict([('sparse_categorical_accuracy', 0.104574844), ('loss', 2.3388205)])
Round  10: OrderedDict([('sparse_categorical_accuracy', 0.29966694), ('loss', 2.089262)])
Round  15: OrderedDict([('sparse_categorical_accuracy', 0.4067398), ('loss', 1.9109797)])
Round  20: OrderedDict([('sparse_categorical_accuracy', 0.5123677), ('loss', 1.6472703)])
Round  25: OrderedDict([('sparse_categorical_accuracy', 0.56416535), ('loss', 1.4362282)])
Round  50: OrderedDict([('sparse_categorical_accuracy', 0.62323666), ('loss', 1.1682972)])
Round  75: OrderedDict([('sparse_categorical_accuracy', 0.55968356), ('loss', 1.4779186)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.382837), ('loss', 1.9680436)])

Теперь мы можем визуализировать точность набора оценок и потерю этих прогонов.

import matplotlib.pyplot as plt
import seaborn as sns

def make_plot(data_frame):
  plt.figure(figsize=(15, 5))

  dff = data_frame.rename(
      columns={'sparse_categorical_accuracy': 'Accuracy', 'loss': 'Loss'})

  plt.subplot(121)
  sns.lineplot(data=dff, x='Round', y='Accuracy', hue='NoiseMultiplier', palette='dark')
  plt.subplot(122)
  sns.lineplot(data=dff, x='Round', y='Loss', hue='NoiseMultiplier', palette='dark')

make_plot(data_frame)

PNG

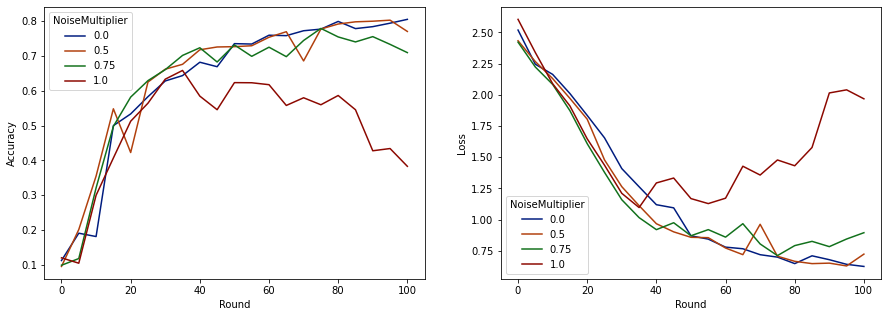
Похоже, что с 50 ожидаемыми клиентами на раунд эта модель может выдерживать множитель шума до 0,5 без ухудшения качества модели. Множитель шума 0,75, кажется, вызывает небольшое ухудшение модели, а 1,0 делает модель расходящейся.

Обычно существует компромисс между качеством модели и конфиденциальностью. Чем выше уровень шума, тем большую конфиденциальность мы можем получить за то же время обучения и количество клиентов. И наоборот, при меньшем уровне шума у нас может быть более точная модель, но нам придется тренироваться с большим количеством клиентов за раунд, чтобы достичь целевого уровня конфиденциальности.

С помощью эксперимента, описанного выше, мы можем решить, что небольшое ухудшение модели на уровне 0,75 приемлемо для более быстрого обучения окончательной модели, но давайте предположим, что мы хотим соответствовать производительности модели с множителем шума 0,5.

Теперь мы можем использовать функции tensorflow_privacy, чтобы определить, сколько ожидаемых клиентов за раунд нам потребуется, чтобы получить приемлемую конфиденциальность. Стандартная практика - выбирать дельту несколько меньше единицы по количеству записей в наборе данных. В этом наборе данных всего 3383 обучаемых пользователя, поэтому давайте стремимся к (2, 1e-5) -DP.

Мы используем простой бинарный поиск по количеству клиентов за раунд. Функция tensorflow_privacy мы используем для оценки эпсилона основана на Wang и соавт. (2018) и Миронов и др. (2019) .

rdp_orders = ([1.25, 1.5, 1.75, 2., 2.25, 2.5, 3., 3.5, 4., 4.5] +
              list(range(5, 64)) + [128, 256, 512])

total_clients = 3383
base_noise_multiplier = 0.5
base_clients_per_round = 50
target_delta = 1e-5
target_eps = 2

def get_epsilon(clients_per_round):
  # If we use this number of clients per round and proportionally
  # scale up the noise multiplier, what epsilon do we achieve?
  q = clients_per_round / total_clients
  noise_multiplier = base_noise_multiplier
  noise_multiplier *= clients_per_round / base_clients_per_round
  rdp = tfp.compute_rdp(
      q, noise_multiplier=noise_multiplier, steps=rounds, orders=rdp_orders)
  eps, _, _ = tfp.get_privacy_spent(rdp_orders, rdp, target_delta=target_delta)
  return clients_per_round, eps, noise_multiplier

def find_needed_clients_per_round():
  hi = get_epsilon(base_clients_per_round)
  if hi[1] < target_eps:
    return hi

  # Grow interval exponentially until target_eps is exceeded.
  while True:
    lo = hi
    hi = get_epsilon(2 * lo[0])
    if hi[1] < target_eps:
      break

  # Binary search.
  while hi[0] - lo[0] > 1:
    mid = get_epsilon((lo[0] + hi[0]) // 2)
    if mid[1] > target_eps:
      lo = mid
    else:
      hi = mid

  return hi

clients_per_round, _, noise_multiplier = find_needed_clients_per_round()
print(f'To get ({target_eps}, {target_delta})-DP, use {clients_per_round} '
      f'clients with noise multiplier {noise_multiplier}.')

To get (2, 1e-05)-DP, use 120 clients with noise multiplier 1.2.

Теперь мы можем подготовить нашу последнюю частную модель к выпуску.

rounds = 100
noise_multiplier = 1.2
clients_per_round = 120

data_frame = pd.DataFrame()
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)

make_plot(data_frame)

Round   0: OrderedDict([('sparse_categorical_accuracy', 0.08260678), ('loss', 2.6334999)])
Round   5: OrderedDict([('sparse_categorical_accuracy', 0.1492212), ('loss', 2.259542)])
Round  10: OrderedDict([('sparse_categorical_accuracy', 0.28847474), ('loss', 2.155699)])
Round  15: OrderedDict([('sparse_categorical_accuracy', 0.3989518), ('loss', 2.0156953)])
Round  20: OrderedDict([('sparse_categorical_accuracy', 0.5086697), ('loss', 1.8261365)])
Round  25: OrderedDict([('sparse_categorical_accuracy', 0.6204692), ('loss', 1.5602393)])
Round  50: OrderedDict([('sparse_categorical_accuracy', 0.70008814), ('loss', 0.91155165)])
Round  75: OrderedDict([('sparse_categorical_accuracy', 0.78421336), ('loss', 0.6820159)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7955525), ('loss', 0.6585961)])

PNG

Как мы видим, окончательная модель имеет те же потери и точность, что и модель, обученная без шума, но эта удовлетворяет (2, 1e-5) -DP.