Pengantar Jaringan RL dan Deep Q

Hak Cipta 2021 The TF-Agents Authors.

pengantar

Pembelajaran penguatan (RL) adalah kerangka kerja umum di mana agen belajar untuk melakukan tindakan di lingkungan untuk memaksimalkan hadiah. Dua komponen utama adalah lingkungan, yang mewakili masalah yang harus dipecahkan, dan agen, yang mewakili algoritma pembelajaran.

Agen dan lingkungan terus berinteraksi satu sama lain. Pada setiap langkah waktu, agen mengambil tindakan terhadap lingkungan berdasarkan kebijakan \(\pi(a_t|s_t)\), di mana \(s_t\) adalah pengamatan saat ini dari lingkungan, dan menerima hadiah \(r_{t+1}\) dan pengamatan berikutnya \(s_{t+1}\) dari lingkungan . Tujuannya adalah untuk memperbaiki kebijakan sehingga memaksimalkan jumlah imbalan (pengembalian).

Catatan: Penting untuk membedakan antara state lingkungan dan observation , yang merupakan bagian dari lingkungan state bahwa agen dapat melihat, misalnya dalam permainan poker, negara lingkungan terdiri dari kartu milik semua pemain dan kartu komunitas, tetapi agen hanya dapat mengamati kartunya sendiri dan beberapa kartu komunitas. Dalam kebanyakan literatur, istilah ini digunakan bergantian dan observasi juga dilambangkan sebagai \(s\).

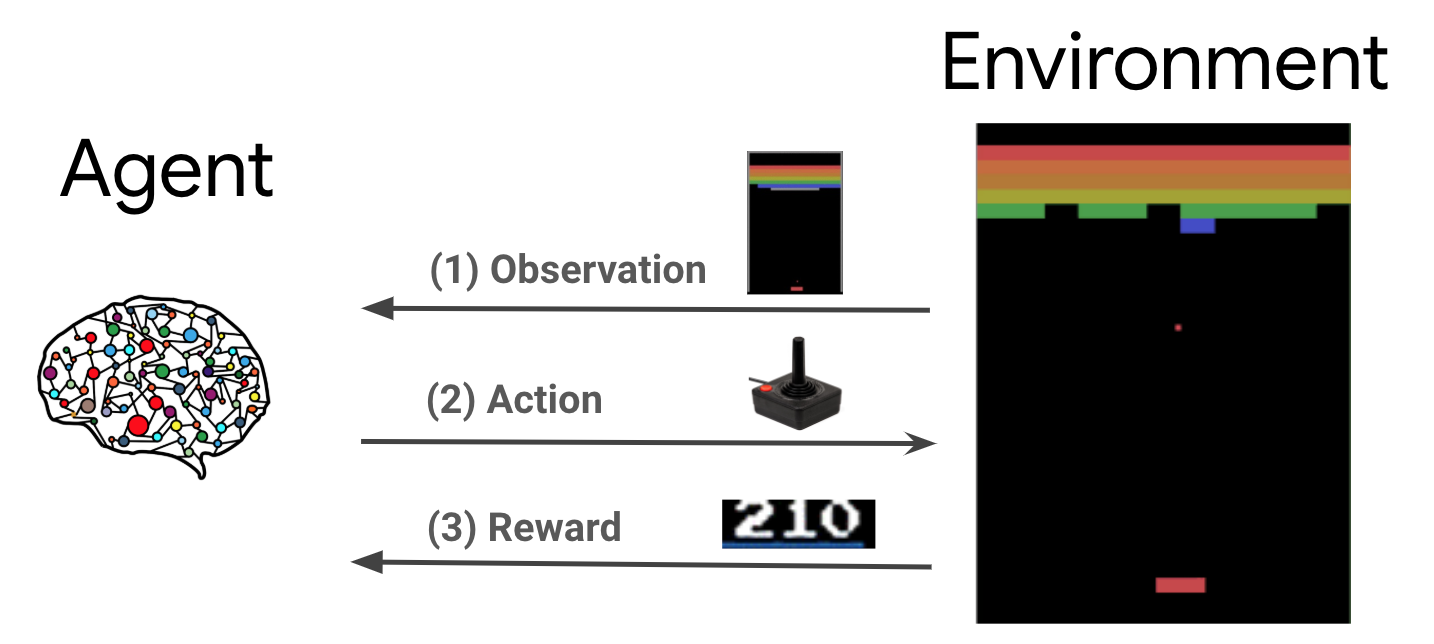
Ini adalah kerangka kerja yang sangat umum dan dapat memodelkan berbagai masalah pengambilan keputusan berurutan seperti game, robotika, dll.

Lingkungan Cartpole

Lingkungan Cartpole adalah salah satu masalah belajar penguatan klasik yang paling terkenal ( "Hello, World!" RL). Sebuah tiang dipasang pada sebuah kereta, yang dapat bergerak sepanjang lintasan tanpa gesekan. Tiang mulai tegak dan tujuannya adalah untuk mencegahnya jatuh dengan mengendalikan gerobak.

• Pengamatan dari lingkungan \(s_t\) adalah vektor 4D mewakili posisi dan kecepatan dari gerobak, dan sudut dan kecepatan sudut tiang.
• Agen dapat mengontrol sistem dengan mengambil salah satu dari 2 tindakan \(a_t\): mendorong gerobak kanan (1) atau kiri (-1).
• Sebuah hadiah \(r_{t+1} = 1\) disediakan untuk setiap timestep bahwa tiang tetap tegak. Episode berakhir ketika salah satu dari berikut ini benar:
  • ujung tiang melewati beberapa batas sudut
  • gerobak bergerak di luar tepi dunia
  • 200 langkah waktu berlalu.

Tujuan dari agen adalah untuk belajar kebijakan \(\pi(a_t|s_t)\) sehingga memaksimalkan jumlah imbalan dalam sebuah episode \(\sum_{t=0}^{T} \gamma^t r_t\). Berikut \(\gamma\) adalah faktor diskon di \([0, 1]\) bahwa diskon masa depan penghargaan relatif terhadap manfaat langsung. Parameter ini membantu kami memfokuskan kebijakan, membuatnya lebih peduli untuk mendapatkan hadiah dengan cepat.

Agen DQN

The DQN (Jauh Q-Network) algoritma dikembangkan oleh DeepMind pada tahun 2015. Itu mampu memecahkan berbagai permainan Atari (beberapa tingkat manusia super) dengan menggabungkan pembelajaran penguatan dan jaringan saraf mendalam pada skala. Algoritma ini dikembangkan dengan meningkatkan algoritma RL klasik yang disebut Q-Learning dengan jaringan saraf yang mendalam dan teknik yang disebut pengalaman replay.

Q-Belajar

Q-Learning didasarkan pada gagasan fungsi-Q. Q-fungsi (alias fungsi nilai state-action) dari kebijakan \(\pi\), \(Q^{\pi}(s, a)\), langkah-langkah pengembalian yang diharapkan atau diskon jumlah imbalan yang diperoleh dari negara \(s\) dengan mengambil tindakan \(a\) pertama dan mengikuti kebijakan \(\pi\) setelahnya. Kami mendefinisikan optimal Q-fungsi \(Q^*(s, a)\) sebagai imbalan yang maksimum yang dapat diperoleh mulai dari pengamatan \(s\), mengambil tindakan \(a\) dan mengikuti kebijakan yang optimal setelahnya. Optimal Q-fungsi mematuhi persamaan Bellman optimalitas berikut:

\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)

Ini berarti bahwa pengembalian maksimal dari negara \(s\) dan tindakan \(a\) adalah jumlah dari langsung reward \(r\) dan kembali (didiskontokan dengan \(\gamma\)) diperoleh dengan mengikuti kebijakan yang optimal setelahnya sampai akhir episode ( yaitu, pahala maksimum dari negara berikutnya \(s'\)). Harapannya dihitung baik atas distribusi manfaat langsung \(r\) dan kemungkinan negara-negara berikutnya \(s'\).

Ide dasar di balik Q-Learning adalah dengan menggunakan persamaan optimalitas Bellman sebagai update berulang \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\), dan dapat menunjukkan bahwa konvergen ini ke optimal \(Q\)-fungsi, yaitu \(Q_i \rightarrow Q^*\) sebagai \(i \rightarrow \infty\) (lihat kertas DQN ).

Q-Learning Mendalam

Untuk sebagian besar masalah, tidak praktis untuk mewakili \(Q\)-fungsi sebagai tabel yang berisi nilai-nilai untuk setiap kombinasi dari \(s\) dan \(a\). Sebaliknya, kita melatih fungsi approximator, seperti jaringan saraf dengan parameter \(\theta\), untuk memperkirakan Q-nilai, yaitu \(Q(s, a; \theta) \approx Q^*(s, a)\). Hal ini dapat dilakukan dengan meminimalkan kerugian berikut pada setiap langkah \(i\):

\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) mana \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)

Di sini, \(y_i\) disebut TD (perbedaan duniawi) sasaran, dan \(y_i - Q\) disebut kesalahan TD. \(\rho\) mewakili distribusi perilaku, distribusi lebih transisi \(\{s, a, r, s'\}\) dikumpulkan dari lingkungan.

Perhatikan bahwa parameter dari iterasi sebelumnya \(\theta_{i-1}\) yang tetap dan tidak diperbarui. Dalam praktiknya, kami menggunakan snapshot parameter jaringan dari beberapa iterasi yang lalu, bukan dari iterasi terakhir. Salinan ini disebut jaringan target.

Q-Learning merupakan algoritma off-kebijakan yang belajar tentang kebijakan serakah \(a = \max_{a} Q(s, a; \theta)\) saat menggunakan kebijakan perilaku yang berbeda untuk bertindak dalam lingkungan / mengumpulkan data. Kebijakan perilaku ini biasanya merupakan \(\epsilon\)kebijakan -greedy yang menyeleksi tindakan serakah dengan probabilitas \(1-\epsilon\) dan tindakan acak dengan probabilitas \(\epsilon\) untuk memastikan cakupan yang baik dari negara ruang-tindakan.

Pengalaman Putar Ulang

Untuk menghindari komputasi ekspektasi penuh dalam kerugian DQN, kita dapat meminimalkannya menggunakan penurunan gradien stokastik. Jika kerugian tersebut dihitung dengan menggunakan hanya transisi terakhir \(\{s, a, r, s'\}\), ini untuk mengurangi standar Q-Learning.

Karya Atari DQN memperkenalkan teknik yang disebut Experience Replay untuk membuat pembaruan jaringan lebih stabil. Pada setiap langkah waktu pengumpulan data, transisi ditambahkan ke buffer melingkar yang disebut replay penyangga. Kemudian selama pelatihan, alih-alih hanya menggunakan transisi terbaru untuk menghitung kerugian dan gradiennya, kami menghitungnya menggunakan kumpulan kecil transisi yang diambil sampelnya dari buffer replay. Ini memiliki dua keuntungan: efisiensi data yang lebih baik dengan menggunakan kembali setiap transisi dalam banyak pembaruan, dan stabilitas yang lebih baik menggunakan transisi yang tidak berkorelasi dalam satu batch.

DQN pada Cartpole di TF-Agents

TF-Agents menyediakan semua komponen yang diperlukan untuk melatih agen DQN, seperti agen itu sendiri, lingkungan, kebijakan, jaringan, buffer replay, loop pengumpulan data, dan metrik. Komponen ini diimplementasikan sebagai fungsi Python atau operasi grafik TensorFlow, dan kami juga memiliki pembungkus untuk mengonversinya. Selain itu, TF-Agents mendukung mode TensorFlow 2.0, yang memungkinkan kami menggunakan TF dalam mode imperatif.

Berikutnya, kita lihat di tutorial untuk melatih agen DQN pada lingkungan Cartpole menggunakan TF-Agen .