 TensorFlow.orgで表示 TensorFlow.orgで表示 |  GoogleColabで実行 GoogleColabで実行 |  GitHubでソースを表示 GitHubでソースを表示 |  ノートブックをダウンロード ノートブックをダウンロード |
pip install -q -U jax jaxlibpip install -q -Uq oryx -Ipip install -q tfp-nightly --upgrade
from functools import partial
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')
import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions
import oryx
確率的プログラミングとは、プログラミング言語の機能を使用して確率的モデルを表現できるという考え方です。ベイジアン推論や周縁化などのタスクは、言語機能として提供され、自動化できる可能性があります。
Oryxは、確率的プログラムがPython関数として表現される確率的プログラミングシステムを提供します。これらのプログラムは、JAXのような構成可能な関数変換を介して変換されます。アイデアは、単純なプログラム(ランダム正規分布からのサンプリングなど)から始めて、それらを一緒に構成してモデル(ベイズニューラルネットワークなど)を形成することです。オリックスのPPL設計の重要な点は、JAXですでに書きたい機能や使用に見えるようにプログラムを有効にすることですが、それらの変形を認識させるために注釈を付けています。
まず、OryxのコアPPL機能をインポートしましょう。
from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest
Oryxの確率的プログラムとは何ですか?
Oryxでは、確率的プログラムは、JAX値と疑似ランダムキーを操作してランダムサンプルを返す純粋なPython関数です。デザインによって、彼らのような変換と互換性がありjitとvmap 。しかし、オリックス確率的プログラミングシステムは、便利な方法であなたの機能に注釈を付けることができますツールを提供します。
純関数のJAX哲学以下、オリックス確率プログラムはJAXかかるPythonの関数であるPRNGKey最初の引数とその後のコンディショニング任意の数の引数として。関数の出力は、「サンプル」とに適用される同一の制限と呼ばれるjit -edとvmap -ed関数は、確率プログラム(例えばないデータ依存制御フロー、副作用なし、等)にも適用されます。これは、「サンプル」がプログラムの実行の内部の値を含む実行トレース全体である多くの命令型確率的プログラミングシステムとは異なります。私たちは、オリックスが使用して内部値にアクセスする方法を後で見るjoint_sample以下で議論を。
Program :: PRNGKey -> ... -> Sample
ここで、「ハローワールド」プログラムがあることから、サンプル対数正規分布。
def log_normal(key):
return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.) 0.8139614 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
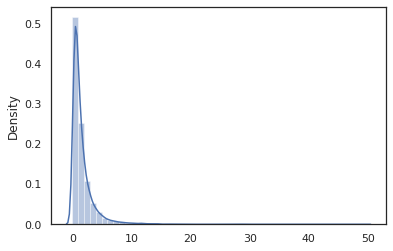
log_normal機能は薄いラッパですTensorflow確率(TFP)が、代わりに呼び出し、分布tfd.Normal(0., 1.).sample 、我々が使用したrandom_variable代わりに。私たちは、後でわかるように、 random_variable他の便利な機能と一緒に、確率的プログラムにオブジェクトを変換することが可能になります。
私たちは、変換することができlog_normal使用してログ・密度関数にlog_prob変換を:
print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()
-0.9189385
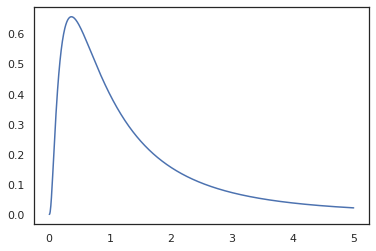
私たちが持つ機能注釈を付けてきたのでrandom_variable 、 log_probへの呼び出しがあったことを認識しているtfd.Normal(0., 1.).sampleし、使用していますtfd.Normal(0., 1.).log_probベース分布を計算しますログ確率。処理するためjnp.exp 、 ppl.log_prob自動的に変更の変数計算に体積変化を追跡し、全単射関数を介して密度を計算します。
オリックスでは、我々はプログラムを取り、機能変換を使用してそれらを変換することができます-例えば、 jax.jitまたはlog_prob 。 Oryxは、どのプログラムでもこれを行うことはできません。ログ密度関数をOryxに登録したサンプリング関数が必要です。幸いなことに、オリックスは自動的に登録TensorFlow確率そのシステムの(TFP)分布を。
Oryxの確率的プログラミングツール
Oryxには、確率的プログラミングを対象としたいくつかの関数変換があります。それらのほとんどを調べて、いくつかの例を示します。最後に、すべてをまとめてMCMCのケーススタディにします。あなたはまたのためのマニュアルを参照してくださいすることができますcore.ppl.transformations詳細について。
random_variable
random_variable機能の二つの主要な部分を有し、その両方は、変換に使用することができる情報をPythonの機能を注釈に焦点を当てました。
random_variableデフォルトでは恒等関数として動作しますが、確率的programs.`に変換オブジェクトにタイプ固有の登録を使用することができます"呼び出し可能なタイプ(Python関数、ラムダ、ため
functools.partialS、等)及び任意のobjectS(JAXなどDeviceArrayS)それだけで、その入力を返します。random_variable(x: object) == x random_variable(f: Callable[...]) == fオリックス自動的に登録TensorFlow確率(TFP)分布の確率を呼び出すプログラムに変換さ分布、
sample方法。random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235Oryxはさらに、TFP分布に関する情報をJAXトレースに埋め込み、ログ密度を自動的に計算できるようにします。
random_variable名、オプションで提供することで、下流の変換のためにそれらを有用なものと缶タグ値nameにキーワード引数をrandom_variable。我々はに配列を渡すときrandom_variableと一緒にname(例えばrandom_variable(x, name='x')それだけで価値と戻り、それをタグ付けします。我々は、呼び出し可能かTFP分布を渡す場合random_variableとの出力サンプルタグプログラムリターンをname。
実行時にこれらの注釈はプログラムのセマンティクスを変更しませんが、変換した場合にのみ(すなわちプログラムは、使用の有無にかかわらず同じ値を返しますrandom_variable )。
両方の機能を一緒に使用する例を見てみましょう。
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
このプログラムでは、中間体のタグを付けてきたzとxの変換になり、 joint_sample 、 intervene 、 conditionalとgraph_replace名前を知っ'z'と'x' 。各変換で名前がどのように使用されるかについては、後で詳しく説明します。
log_prob
log_prob関数変換は、対数密度関数にオリックス確率プログラムを変換します。この対数密度関数は、プログラムから潜在的なサンプルを入力として取得し、基礎となるサンプリング分布の下でその対数密度を返します。
log_prob :: Program -> (Sample -> LogDensity)
ようrandom_variable 、そのように、TFP分布が自動的に登録されているタイプのレジストリを介して動作log_prob(tfd.Normal(0., 1.))呼び出しtfd.Normal(0., 1.).log_prob Pythonの関数については、しかし、 log_prob文をサンプリングするためのJAXとルックスを使用してプログラムをトレースします。 log_prob変換は、ランダムな変数を返すほとんどのプログラム、直接または可逆変換を経由してではなく、プログラムのサンプル値は内部的に返されないことに取り組んでいます。それはプログラムで必要な操作を反転することができない場合は、 log_probエラーをスローします。
ここではいくつかの例ですlog_prob各種のプログラムに適用されるが。
-
log_probTFP分布(またはその他の登録タイプ)から直接、サンプルプログラム上で動作し、その値を返します。
def normal(key):
return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))
-0.9189385
-
log_prob(例えば全単射関数を用いてランダム変量を変換するプログラムからのサンプルの対数密度を計算することができjnp.exp、jnp.tanh、jnp.split)。
def log_normal(key):
return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))
-1.159165
サンプルを計算するためにlog_normalの反転するログ密度、我々まず必要exp 、服用logのサンプルを、その後の逆対数-DETヤコビアンを使用して、ボリューム変更の補正を加えるexp (参照の変更を変数のウィキペディアからの式)。
-
log_probPythonの辞書やタプルのようなサンプルの出力構造そのプログラムで動作します。
def normal_2d(key):
x = random_variable(
tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
x1, x2 = jnp.split(x, 2, 0)
return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))
{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546
-
log_prob必要なときに変数の明確に定義された変化を介してその基地サンプリング値で返される値を接続しようとも、順方向および逆値(およびそれらのログDETヤコビアン)を計算する、関数のトレース計算グラフを歩きます。次のサンプルプログラムを見てください。
def complex_program(key):
k1, k2 = random.split(key)
z = random_variable(tfd.Normal(0., 1.))(k1)
x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))
(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32)) -1.0967848
このプログラムでは、我々のサンプルxの条件付きz 、我々はの値必要な意味z 、我々はの対数密度を計算することができます前に、 x 。しかし、計算するためにz 、我々は最初に反転する必要がjnp.expに適用z 。したがって、の対数濃度を計算するためにxとz 、 log_prob第反転する第一の出力を必要とし、その後を通して前方に渡すjax.nn.reluの平均を計算するためにp(x | z) 。
詳細についてはlog_prob 、あなたはを参照することができcore.interpreters.log_prob 。インプリメンテーションでは、 log_prob密接オフ基づくinverse JAX変換。詳細学ぶためにinverse参照してくださいcore.interpreters.inverse 。
joint_sample
より複雑で興味深いプログラムを定義するために、いくつかの潜在確率変数、つまり観測されていない値を持つ確率変数を使用します。のは、参照してみましょうlatent_normalプログラムをサンプリングランダム値z別のランダム値の平均値として使用されているx 。
def latent_normal(key):
z_key, x_key = random.split(key)
z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)
このプログラムでは、 z我々だけ呼び出すようにした場合の潜在そうですlatent_normal(random.PRNGKey(0))私たちは、実際の値が分からないのでしょうz生成を担当してx 。
joint_sampleそれらの値に戻る辞書マッピング列名(タグ)は別のプログラムにプログラムを変換する変換です。動作させるには、潜在変数にタグを付けて、変換された関数の出力に確実に表示されるようにする必要があります。
joint_sample(latent_normal)(random.PRNGKey(0))
{'x': DeviceArray(0.01873656, dtype=float32),
'z': DeviceArray(0.14389044, dtype=float32)}
なおjoint_sampleその潜在値に対する関節分布サンプルは、私たちはさらにそれを変換することができる別のプログラムに変換するプログラム。 MCMCやVIのようなアルゴリズムの場合、推論手順の一部として同時分布の対数確率を計算するのが一般的です。 log_prob(latent_normal)それが出て疎外必要があるため、動作しませんz 、私たちが使用することができますlog_prob(joint_sample(latent_normal))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))
-50.03529 -5049.535
このような一般的なパターンであるため、オリックスも有するjoint_log_probのちょうど組成物で形質転換log_probとjoint_sample 。
print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))
-50.03529 -5049.535
block
block変換は、プログラム名のシーケンスを取り込み、挙動は同じ(のような下流の変換でいること以外は、プログラム返しjoint_sample )、提供名は無視されています。ここでの例block便利である尤度にサンプリングされた値を「ブロッキング」によって潜在変数オーバー前に関節分布に変換されます。例えば、取るlatent_normal最初描く、 z ~ N(0, 1)次にx | z ~ N(z, 1e-1) 。 block(latent_normal, names=['x'])獣皮というプログラムであるx私たちがしなければ名前は、そうjoint_sample(block(latent_normal, names=['x'])) 、我々だけで辞書を得るzそれに。
blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))
{'z': DeviceArray(0.14389044, dtype=float32)}
intervene
intervene外部からの値を持つ確率プログラムに変換切り詰めサンプルを。私たちに戻ってlatent_normalプログラムを、我々は同じプログラムを実行しているに興味を持っていたが、望んでいたとしましょうz新しいプログラムを書くよりも、むしろ4に固定されるように、我々は使用することができinterveneの値上書きするz 。
intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
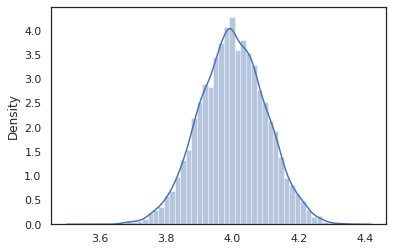
intervened機能サンプルからp(x | do(z = 4))我々は場合だけ標準正規分布は4を中心とするintervene特定の値に、その値がもはやランダム変数と見なされています。ことをこれは意味z実行中に値がタグ付けされないであろうintervened 。
conditional
conditional変換プログラムこれらの潜在値上の一のその条件に試料を潜在値こと。私たちに戻ってlatent_normalサンプルプログラム、 p(x)潜伏してz 、我々は条件付きのプログラムに変換することができますp(x | z) 。
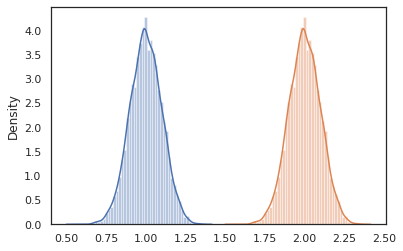
cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()
99.87485 49.874847 /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning) /home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms). warnings.warn(msg, FutureWarning)
nest
より複雑なプログラムを構築するために確率プログラムを作成し始めるとき、いくつかの重要なロジックを持つ関数を再利用するのが一般的です。我々はベイジアンニューラルネットワークを構築したい場合たとえば、そこに重要であるかもしれないdenseそのサンプルの重みプログラムとフォワード・パスを実行します。
我々は機能を再利用する場合は、しかし、我々のような変換によって禁止されて最終的なプログラムに重複するタグ付けされた値で終わるかもしれないjoint_sample 。我々は使用することができますnest名前の範囲内の任意のサンプルは、ネストされた辞書に挿入されたタグ「スコープ」を作成します。
def f(key):
return random_variable(tfd.Normal(0., 1.), name='x')(key)
def g(key):
k1, k2 = random.split(key)
return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))
{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }
ケーススタディ:ベイジアンニューラルネットワーク
のは、古典的な分類のためのベイジアンニューラルネットワークを訓練で私たちの手を試してみましょうフィッシャーアイリスデータセットを。比較的小さく低次元なので、MCMCで後方を直接サンプリングしてみることができます。
まず、Oryxからデータセットといくつかの追加ユーティリティをインポートしましょう。
from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']
num_features = features.shape[-1]
num_classes = len(iris.target_names)
from oryx.experimental import mcmc
from oryx.util import summary, get_summaries
まず、重みとバイアスよりも通常の優先順位を持つ高密度レイヤーを実装します。これを行うには、まず定義dense所望の出力の寸法及び活性化機能を取り込み高階関数を。 dense機能は、条件付き分布を表す確率プログラム返しp(h | x) h緻密層の出力であり、 xその入力されています。これは、最初のサンプル重量とバイアスし、その後にそれらを適用しx 。
def dense(dim_out, activation=jax.nn.relu):
def forward(key, x):
dim_in = x.shape[-1]
w_key, b_key = random.split(key)
w = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
name='w')(w_key)
b = random_variable(
tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
name='b')(b_key)
return activation(jnp.dot(w, x) + b)
return forward
いくつかの構成にはdense層を一緒に、我々は実装しますmlp隠されたサイズのリストとクラスの数になります(多層パーセプトロン)高階関数を。これは、繰り返し呼び出すことプログラムを返すdense 、適切な使用hidden_sizeし、最終的に、最終的な層に各クラスのlogitsを返します。使用に注意してくださいnest各レイヤーの名前スコープを作成します。
def mlp(hidden_sizes, num_classes):
num_hidden = len(hidden_sizes)
def forward(key, x):
keys = random.split(key, num_hidden + 1)
for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
logits = nest(dense(num_classes, activation=lambda x: x),
scope=f'layer_{num_hidden + 1}')(keys[-1], x)
return logits
return forward
完全なモデルを実装するには、ラベルをカテゴリ確率変数としてモデル化する必要があります。私たちは、定義しますpredictのデータセットに取る関数xs 、その後に渡されます(機能) mlp使用してvmap 。私たちが使用している場合vmap(partial(mlp, mlp_key)) 、我々は重みの単一のセットをサンプリングしますが、すべての入力を介してフォワード・パスをマップxs 。これは、一連の生産logits独立したカテゴリ分布をパラメータ化。
def predict(mlp):
def forward(key, xs):
mlp_key, label_key = random.split(key)
logits = vmap(partial(mlp, mlp_key))(xs)
return random_variable(
tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
return forward
それがフルモデルです! MCMCを使用して、与えられたデータのBNN重みの後方をサンプリングしてみましょう。最初、私たちは使用してBNN「テンプレート」を構築mlp 。
bnn = mlp([200, 200], num_classes)
私たちのマルコフ連鎖の開始ポイントを構築するために、我々は使用することができますjoint_sampleダミー入力して。
weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())
dict_keys(['layer_1', 'layer_2', 'layer_3'])
多くの推論アルゴリズムでは、同時分布の対数確率を計算するだけで十分です。今度は私たちが観察しましょうxし、事後サンプリングするp(z | x) 。複雑な分布のために、我々は、アウト過小評価することはできませんx (のためのけれどもlatent_normalたちができる)が、我々は、非正規化対数密度計算することができるlog p(z, x) x特定の値に固定されます。 MCMCで正規化されていない対数確率を使用して、事後をサンプリングできます。この「固定された」ログ確率関数を書いてみましょう。
def target_log_prob(weights):
return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)
今、私たちは使用することができますtfp.mcmc当社の非正規化ログ密度関数を使用して、後方をサンプリングします。私たちは、ネストされた重みの「フラット化」のバージョンを使用する必要がありますことをご注意と互換性があるように辞書tfp.mcmc我々は平らにし、非平坦化するためにJAXの木のユーティリティを使用して、。
@jit
def run_chain(key, weights):
flat_state, sample_tree = jax.tree_flatten(weights)
def flat_log_prob(*states):
return target_log_prob(jax.tree_unflatten(sample_tree, states))
def trace_fn(_, results):
return results.inner_results.accepted_results.target_log_prob
flat_states, log_probs = tfp.mcmc.sample_chain(
1000,
num_burnin_steps=9000,
kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
9000, target_accept_prob=0.7),
trace_fn=trace_fn,
current_state=flat_state,
seed=key)
samples = jax.tree_unflatten(sample_tree, flat_states)
return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)
plt.plot(log_probs)
plt.show()
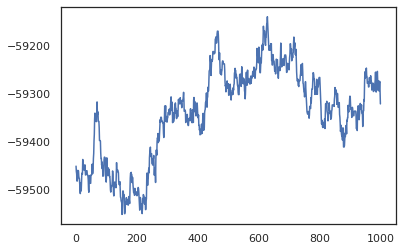
サンプルを使用して、トレーニング精度のベイズモデル平均化(BMA)推定を行うことができます。それを計算するために、我々は使用することができinterveneでbnnキーからサンプリングされているものの代わりに「注入」後部重みに。各後部サンプルのための各データポイントのlogitsを計算するために、我々は倍増することができますvmap上posterior_weightsとfeatures 。
output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)
print('Average sample accuracy:', (
output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())
Average sample accuracy: 0.9874067 BMA accuracy: 0.99333334
結論
Oryxでは、確率的プログラムは、入力として(疑似)ランダム性を取り込む単なるJAX関数です。 OryxはJAXの関数変換システムと緊密に統合されているため、JAXコードを記述しているように、確率的プログラムを記述および操作できます。これにより、複雑なモデルを構築して推論を行うためのシンプルで柔軟なシステムが実現します。
