Lập trình xác suất trong Oryx

pip install -q -U jax jaxlib
pip install -q -Uq oryx -I
pip install -q tfp-nightly --upgrade

from functools import partial

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')

import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random

from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions

import oryx

Lập trình xác suất là ý tưởng mà chúng ta có thể thể hiện các mô hình xác suất bằng cách sử dụng các tính năng từ một ngôn ngữ lập trình. Sau đó, các tác vụ như suy luận Bayes hoặc định biên được cung cấp dưới dạng các tính năng ngôn ngữ và có thể được tự động hóa.

Oryx cung cấp một hệ thống lập trình xác suất trong đó các chương trình xác suất chỉ được thể hiện dưới dạng các hàm Python; các chương trình này sau đó được chuyển đổi thông qua các phép biến đổi chức năng có thể kết hợp như trong JAX! Ý tưởng là bắt đầu với các chương trình đơn giản (như lấy mẫu từ một thông thường ngẫu nhiên) và kết hợp chúng lại với nhau để tạo thành các mô hình (như mạng nơ-ron Bayes). Một điểm quan trọng của thiết kế PPL Oryx là để cho phép các chương trình để trông giống như chức năng bạn muốn đã viết và sử dụng trong JAX, nhưng được chú thích để làm biến đổi nhận thức của họ.

Đầu tiên hãy nhập chức năng PPL cốt lõi của Oryx.

from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest

Các chương trình xác suất trong Oryx là gì?

Trong Oryx, các chương trình xác suất chỉ là các hàm Python thuần túy hoạt động trên các giá trị JAX và khóa giả ngẫu nhiên và trả về một mẫu ngẫu nhiên. Theo thiết kế, chúng phù hợp với biến đổi như jit và vmap . Tuy nhiên, hệ thống lập trình xác suất Oryx cung cấp công cụ cho phép bạn chú thích chức năng của mình theo những cách hữu ích.

Sau khi triết lý JAX chức năng thuần túy, một chương trình xác suất Oryx là một hàm Python mà phải mất một JAX PRNGKey như là đối số đầu tiên của mình và bất kỳ số lượng đối số điều sau này. Kết quả của hàm được gọi là một "mẫu" và những hạn chế tương tự áp dụng cho jit -ed và vmap chức năng -ed áp dụng đối với các chương trình xác suất (ví dụ như không có luồng dữ liệu phụ thuộc vào kiểm soát, không có tác dụng phụ, vv). Điều này khác với nhiều hệ thống lập trình xác suất bắt buộc trong đó 'mẫu' là toàn bộ dấu vết thực thi, bao gồm các giá trị bên trong quá trình thực thi của chương trình. Chúng ta sẽ thấy sau này như thế nào Oryx có thể truy cập các giá trị nội bộ bằng cách sử dụng joint_sample , thảo luận dưới đây.

Program :: PRNGKey -> ... -> Sample

Dưới đây là một chương trình "hello world" mà mẫu từ một phân phối log-bình thường .

def log_normal(key):
  return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))

print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
0.8139614
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

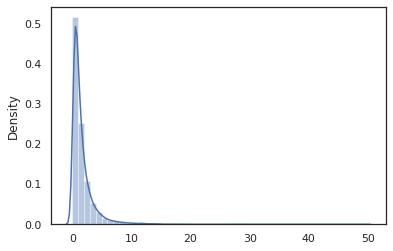
Các log_normal chức năng là một wrapper mỏng xung quanh một Tensorflow Xác suất (TFP) phân phối, nhưng thay vì gọi tfd.Normal(0., 1.).sample , chúng tôi đã sử dụng random_variable để thay thế. Như chúng ta sẽ thấy sau này, random_variable cho phép chúng ta chuyển đổi các đối tượng vào các chương trình xác suất, cùng với chức năng hữu ích khác.

Chúng tôi có thể chuyển đổi log_normal vào một hàm log-mật độ sử dụng log_prob chuyển đổi:

print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()

-0.9189385

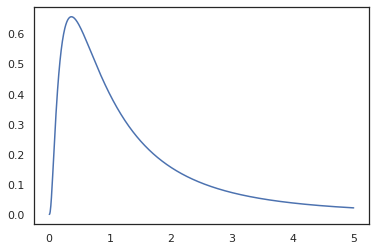
Bởi vì chúng tôi đã chú thích chức năng với random_variable , log_prob là nhận thức được rằng có một cuộc gọi đến tfd.Normal(0., 1.).sample và sử dụng tfd.Normal(0., 1.).log_prob để tính toán sự phân bố cơ sở đăng nhập thử nghiệm. Để xử lý các jnp.exp , ppl.log_prob tự động tính toán mật độ thông qua chức năng song ánh, theo dõi các thay đổi khối lượng trong việc tính toán sự thay đổi-of-biến.

Trong Oryx, chúng ta có thể lấy chương trình và chuyển đổi chúng bằng biến đổi chức năng - ví dụ, jax.jit hoặc log_prob . Oryx không thể làm điều này với bất kỳ chương trình nào; nó yêu cầu các chức năng lấy mẫu đã đăng ký chức năng mật độ nhật ký của họ với Oryx. May mắn thay, Oryx tự động đăng ký TensorFlow Xác suất phân phối (TFP) trong hệ thống của mình.

Các công cụ lập trình xác suất của Oryx

Oryx có một số biến đổi chức năng hướng tới lập trình xác suất. Chúng tôi sẽ xem xét hầu hết chúng và cung cấp một số ví dụ. Cuối cùng, chúng tôi sẽ tổng hợp tất cả lại thành một nghiên cứu điển hình MCMC. Bạn cũng có thể tham khảo các tài liệu cho core.ppl.transformations để biết thêm chi tiết.

random_variable

random_variable có hai mảnh chính của chức năng, cả hai đều tập trung vào chú thích chức năng Python với thông tin có thể được sử dụng trong biến đổi.

1. random_variable 'hoạt động như chức năng nhận dạng bằng cách mặc định, nhưng có thể sử dụng đăng ký loại cụ thể các đối tượng chuyển đổi thành programs.` xác suất

   Đối với các loại callable (chức năng Python, lambdas, functools.partial s, vv) và tùy object s (như JAX DeviceArray s) nó sẽ chỉ trở lại đầu vào của nó.

   random_variable(x: object) == x
   random_variable(f: Callable[...]) == f
   

   Oryx tự động đăng ký TensorFlow Xác suất (TFP) phân phối, mà được chuyển đổi thành chương trình xác suất mà gọi của phân phối sample phương pháp.

   random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235
   

   Oryx cũng nhúng thông tin về phân phối TFP vào dấu vết JAX để cho phép tự động tính toán mật độ nhật ký.

2. random_variable giá trị có thể tag với tên, làm cho chúng hữu ích cho biến đổi hạ lưu, bằng cách cung cấp một tùy chọn name tham số từ khóa để random_variable . Khi chúng tôi vượt qua một mảng vào random_variable cùng với một name (ví dụ random_variable(x, name='x') ), nó chỉ thẻ giá trị và trả về nó. Nếu chúng ta vượt qua trong một callable hoặc phân phối TFP, random_variable lợi nhuận một chương trình thẻ mẫu sản lượng của nó với name .

Những chú thích này không làm thay đổi ngữ nghĩa của chương trình khi thực hiện, nhưng chỉ khi chuyển đổi (tức là chương trình sẽ trả về giá trị tương tự có hoặc không có việc sử dụng các random_variable ).

Hãy xem qua một ví dụ trong đó chúng ta sử dụng cả hai phần chức năng cùng nhau.

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

Trong chương trình này, chúng tôi đã gắn thẻ các chất trung gian z và x , mà làm cho biến đổi joint_sample , intervene , conditional và graph_replace biết trong những cái tên 'z' và 'x' . Chúng ta sẽ xem xét chính xác cách mỗi chuyển đổi sử dụng tên sau.

log_prob

Các log_prob chuyển đổi chức năng chuyển đổi một Oryx chương trình xác suất vào hàm log-mật độ của nó. Hàm mật độ nhật ký này lấy một mẫu tiềm năng từ chương trình làm đầu vào và trả về mật độ nhật ký của nó theo phân phối lấy mẫu cơ bản.

log_prob :: Program -> (Sample -> LogDensity)

Giống như random_variable , nó hoạt động thông qua một registry của các loại nơi phân phối TFP sẽ được tự động đăng ký, vì vậy log_prob(tfd.Normal(0., 1.)) gọi tfd.Normal(0., 1.).log_prob . Tuy nhiên, đối với chức năng Python, log_prob dấu vết các chương trình sử dụng JAX và ngoại hình cho lấy mẫu báo cáo. Các log_prob chuyển đổi hoạt động trên hầu hết các chương trình quay trở lại các biến ngẫu nhiên, trực tiếp hoặc thông qua biến đổi nghịch nhưng không phải trên các chương trình mà các giá trị mẫu nội bộ mà không được trả lại. Nếu nó không thể đảo ngược các hoạt động cần thiết trong chương trình, log_prob sẽ ném một lỗi.

Dưới đây là một số ví dụ về log_prob áp dụng cho các chương trình khác nhau.

1. log_prob hoạt động trên các chương trình trực tiếp mẫu từ phân phối TFP (hoặc các loại đăng ký khác) và trở về giá trị của họ.

def normal(key):
  return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))

-0.9189385

1. log_prob có khả năng tính toán log-mật độ của các mẫu từ các chương trình chuyển đổi variates ngẫu nhiên sử dụng chức năng song ánh (ví dụ jnp.exp , jnp.tanh , jnp.split ).

def log_normal(key):
  return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))

-1.159165

Để tính toán một mẫu từ log_normal 's log-mật, trước tiên chúng ta cần phải đảo ngược exp , lấy log của mẫu, và sau đó thêm một sự điều chỉnh âm lượng thay đổi bằng cách sử dụng log-det ngược Jacobian của exp (xem sự thay đổi của biến thức từ Wikipedia).

1. log_prob làm việc với chương trình cơ cấu sản lượng mẫu thích, từ điển Python hoặc tuples.

def normal_2d(key):
  x = random_variable(
    tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
  x1, x2 = jnp.split(x, 2, 0)
  return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))

{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546

1. log_prob đi biểu đồ tính toán truy chức năng, tính cả hai giá trị về phía trước và ngược lại (và log-det của họ Jacobians) khi cần thiết trong một nỗ lực để kết nối các giá trị trở lại với cơ sở giá trị lấy mẫu của họ thông qua một sự thay đổi rõ ràng của các biến. Lấy chương trình ví dụ sau:

def complex_program(key):
  k1, k2 = random.split(key)
  z = random_variable(tfd.Normal(0., 1.))(k1)
  x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
  return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))

(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32))
-1.0967848

Trong chương trình này, chúng tôi mẫu x có điều kiện về z , có nghĩa là chúng ta cần giá trị của z trước khi chúng tôi có thể tính toán log-mật độ x . Tuy nhiên, để tính toán z , trước tiên chúng ta phải đảo ngược jnp.exp áp dụng cho z . Như vậy, để tính toán log-mật độ của x và z , log_prob nhu cầu đầu tiên nghịch sản lượng đầu tiên, và sau đó vượt qua nó về phía trước thông qua jax.nn.relu để tính toán giá trị trung bình của p(x | z) .

Lưu ý: trong khi log_prob sẽ không làm việc trên các chương trình mà các biến ngẫu nhiên mẫu mà không được trở lại như đầu ra, joint_sample có thể chuyển đổi một chương trình thành một mà không.

Để biết thêm thông tin về log_prob , bạn có thể tham khảo core.interpreters.log_prob . Trong thực hiện, log_prob là chặt chẽ dựa tắt của inverse chuyển JAX; để tìm hiểu thêm về inverse , xem core.interpreters.inverse .

joint_sample

Để xác định các chương trình phức tạp và thú vị hơn, chúng tôi sẽ sử dụng một số biến ngẫu nhiên tiềm ẩn, tức là các biến ngẫu nhiên có giá trị không được quan sát. Hãy tham khảo các latent_normal chương trình mẫu một giá trị ngẫu nhiên z được sử dụng như giá trị trung bình của một giá trị ngẫu nhiên x .

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

Trong chương trình này, z là rất tiềm ẩn nếu chúng ta chỉ cần gọi latent_normal(random.PRNGKey(0)) chúng ta sẽ không biết giá trị thực tế của z đó là trách nhiệm tạo ra x .

joint_sample là một sự chuyển đổi đó biến đổi một chương trình vào một chương trình khác mà lợi nhuận một cuốn từ điển chuỗi lập bản đồ tên (tags) để giá trị của họ. Để hoạt động, chúng ta cần đảm bảo rằng chúng ta gắn thẻ các biến tiềm ẩn để đảm bảo chúng xuất hiện trong đầu ra của hàm đã biến đổi.

joint_sample(latent_normal)(random.PRNGKey(0))

{'x': DeviceArray(0.01873656, dtype=float32),
 'z': DeviceArray(0.14389044, dtype=float32)}

Lưu ý rằng joint_sample biến đổi một chương trình vào một chương trình khác mà mẫu phân phối của doanh trên các giá trị tiềm ẩn của nó, vì vậy chúng tôi có thể tiếp tục chuyển hóa nó. Đối với các thuật toán như MCMC và VI, người ta thường tính xác suất log của phân phối chung như một phần của quy trình suy luận. log_prob(latent_normal) không làm việc vì nó đòi hỏi marginalizing ra z , nhưng chúng ta có thể sử dụng log_prob(joint_sample(latent_normal)) .

print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))

-50.03529
-5049.535

Bởi vì đây là một mô hình phổ biến như vậy, Oryx cũng có một joint_log_prob chuyển đổi mà chỉ là thành phần của log_prob và joint_sample .

print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))

-50.03529
-5049.535

block

Các block chuyển đổi mất trong một chương trình và một chuỗi các tên và trả về một chương trình mà cư xử hệt ngoại trừ trong biến đổi hạ lưu (như joint_sample ), những cái tên được cung cấp sẽ được bỏ qua. Một ví dụ về nơi block là tiện dụng được chuyển đổi một phân phối chung vào một trước khi qua các biến tiềm ẩn bằng cách "chặn" các giá trị lấy mẫu trong khả năng. Ví dụ, hãy latent_normal , mà đầu tiên vẽ một z ~ N(0, 1) sau đó một x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) là một chương trình mà da của x tên, vì vậy nếu chúng ta làm joint_sample(block(latent_normal, names=['x'])) , chúng tôi có được một cuốn từ điển chỉ với z trong đó .

blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))

{'z': DeviceArray(0.14389044, dtype=float32)}

intervene

Các intervene clobbers chuyển đổi mẫu trong một chương trình xác suất với giá trị từ bên ngoài. Trở lại với chúng tôi latent_normal chương trình, chúng ta hãy nói chúng tôi đã quan tâm đến việc chạy chương trình tương tự nhưng muốn z được cố định để 4. Thay vì viết một chương trình mới, chúng ta có thể sử dụng intervene để ghi đè lên giá trị của z .

intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();

/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

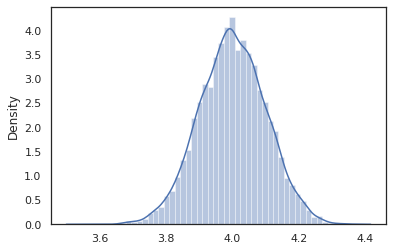
Các intervened mẫu chức năng từ p(x | do(z = 4)) mà chỉ là một phân phối chuẩn chuẩn tập trung ở 4. Khi chúng ta intervene vào một giá trị đặc biệt, giá trị đó không còn được coi là một biến ngẫu nhiên. Điều này có nghĩa rằng một z giá trị sẽ không được gắn thẻ trong khi thực hiện intervened .

conditional

conditional biến đổi một chương trình mẫu tiềm ẩn giá trị vào một trong những điều kiện về những giá trị tiềm ẩn. Quay trở lại với chúng tôi latent_normal chương trình, trong đó mẫu p(x) với một tiềm ẩn z , chúng tôi có thể chuyển đổi nó thành một chương trình có điều kiện p(x | z) .

cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()

99.87485
49.874847
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

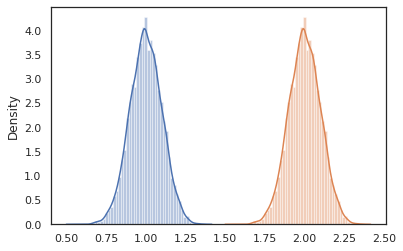
nest

Khi chúng ta bắt đầu soạn các chương trình xác suất để xây dựng những chương trình phức tạp hơn, chúng ta thường sử dụng lại các hàm có một số logic quan trọng. Ví dụ, nếu chúng ta muốn xây dựng một mạng lưới thần kinh Bayesian, có thể có một quan trọng dense chương trình mẫu trọng và thực thi một về phía trước vượt qua.

Nếu chúng ta tái sử dụng các chức năng, tuy nhiên, chúng ta có thể kết thúc với giá trị được gắn thẻ trùng lặp trong chương trình cuối cùng, đó là không được phép bởi biến đổi như joint_sample . Chúng tôi có thể sử dụng nest để tạo ra thẻ "phạm vi", nơi bất kỳ mẫu bên trong một phạm vi tên sẽ được chèn vào một cuốn từ điển lồng nhau.

def f(key):
  return random_variable(tfd.Normal(0., 1.), name='x')(key)

def g(key):
  k1, k2 = random.split(key)
  return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))

{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
 'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }

Nghiên cứu điển hình: Mạng nơ-ron Bayes

Hãy thử tay của chúng tôi tại đào tạo một mạng lưới thần kinh Bayesian để phân loại cổ điển Fisher Iris dataset. Nó tương đối nhỏ và có chiều thấp nên chúng tôi có thể thử lấy mẫu trực tiếp phần sau với MCMC.

Đầu tiên, hãy nhập tập dữ liệu và một số tiện ích bổ sung từ Oryx.

from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']

num_features = features.shape[-1]
num_classes = len(iris.target_names)

from oryx.experimental import mcmc
from oryx.util import summary, get_summaries

Chúng tôi bắt đầu bằng cách triển khai một lớp dày đặc, lớp này sẽ có giá trị gốc bình thường so với trọng lượng và độ lệch. Để làm điều này, đầu tiên chúng ta định nghĩa một dense chức năng bậc cao mà mất trong kích thước đầu ra và kích hoạt chức năng mong muốn. Các dense hàm trả về một chương trình xác suất đại diện cho một phân phối có điều kiện p(h | x) nơi h là sản phẩm của một lớp dày đặc và x là đầu vào của nó. Nó mẫu đầu tiên cân nặng và thiên vị và sau đó áp dụng chúng để x .

def dense(dim_out, activation=jax.nn.relu):
  def forward(key, x):
    dim_in = x.shape[-1]
    w_key, b_key = random.split(key)
    w = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
          name='w')(w_key)
    b = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
          name='b')(b_key)
    return activation(jnp.dot(w, x) + b)
  return forward

Để soạn một vài dense lớp với nhau, chúng tôi sẽ thực hiện một mlp (đa Perceptron) chức năng bậc cao mà mất trong một danh sách các kích cỡ ẩn và một số lớp. Nó trả về một chương trình mà liên tục gọi dense sử dụng thích hợp hidden_size và cuối cùng trả logits cho mỗi lớp trong lớp chính thức. Lưu ý việc sử dụng các nest mà tạo ra phạm vi tên cho mỗi lớp.

def mlp(hidden_sizes, num_classes):
  num_hidden = len(hidden_sizes)
  def forward(key, x):
    keys = random.split(key, num_hidden + 1)
    for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
      x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
    logits = nest(dense(num_classes, activation=lambda x: x),
                  scope=f'layer_{num_hidden + 1}')(keys[-1], x)
    return logits
  return forward

Để triển khai mô hình đầy đủ, chúng ta sẽ cần lập mô hình các nhãn dưới dạng các biến ngẫu nhiên phân loại. Chúng tôi sẽ xác định một predict chức năng mà mất trong một tập dữ liệu của xs (tính năng) sau đó được truyền vào một mlp sử dụng vmap . Khi chúng ta sử dụng vmap(partial(mlp, mlp_key)) , chúng tôi nếm thử một bộ trọng lượng, nhưng bản đồ đường chuyền về phía trước trên tất cả các đầu vào xs . Điều này tạo ra một tập hợp các logits mà parameterizes phân phối phân loại độc lập.

def predict(mlp):
  def forward(key, xs):
    mlp_key, label_key = random.split(key)
    logits = vmap(partial(mlp, mlp_key))(xs)
    return random_variable(
        tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
  return forward

Đó là mô hình đầy đủ! Hãy sử dụng MCMC để lấy mẫu sau của dữ liệu trọng số BNN đã cho; đầu tiên chúng ta xây dựng một BNN "mẫu" sử dụng mlp .

bnn = mlp([200, 200], num_classes)

Để xây dựng một điểm khởi đầu cho chuỗi Markov của chúng tôi, chúng tôi có thể sử dụng joint_sample với một đầu vào dummy.

weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())

dict_keys(['layer_1', 'layer_2', 'layer_3'])

Việc tính toán xác suất nhật ký phân phối chung là đủ cho nhiều thuật toán suy luận. Hãy bây giờ nói rằng chúng ta quan sát x và muốn lấy mẫu sau p(z | x) . Đối với các bản phân phối phức tạp, chúng tôi sẽ không thể để cách ly ra x (mặc dù cho latent_normal chúng ta có thể) nhưng chúng ta có thể tính toán một unnormalized mật độ ghi log p(z, x) nơi x là cố định một giá trị cụ thể. Chúng ta có thể sử dụng xác suất nhật ký không chuẩn hóa với MCMC để lấy mẫu sau. Hãy viết hàm prob log "được ghim" này.

def target_log_prob(weights):
  return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)

Bây giờ chúng ta có thể sử dụng tfp.mcmc để lấy mẫu sau sử dụng hàm mật độ log unnormalized của chúng tôi. Lưu ý rằng chúng tôi sẽ phải sử dụng một "phẳng" phiên bản của trọng lượng lồng nhau của chúng tôi từ điển để tương thích với tfp.mcmc , vì vậy chúng tôi sử dụng các tiện ích cây JAX để san bằng và unflatten.

@jit
def run_chain(key, weights):
  flat_state, sample_tree = jax.tree_flatten(weights)

  def flat_log_prob(*states):
    return target_log_prob(jax.tree_unflatten(sample_tree, states))

  def trace_fn(_, results):
    return results.inner_results.accepted_results.target_log_prob

  flat_states, log_probs = tfp.mcmc.sample_chain(
    1000,
    num_burnin_steps=9000,
    kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
        tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
        9000, target_accept_prob=0.7),
    trace_fn=trace_fn,
    current_state=flat_state,
    seed=key)
  samples = jax.tree_unflatten(sample_tree, flat_states)
  return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)

plt.plot(log_probs)
plt.show()

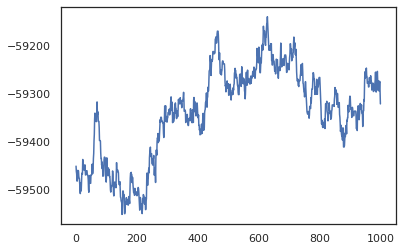
Chúng tôi có thể sử dụng các mẫu của mình để lấy ước tính trung bình theo mô hình Bayesian (BMA) về độ chính xác của quá trình huấn luyện. Để tính toán nó, chúng ta có thể sử dụng intervene với bnn để "bơm" sau trọng lượng ở vị trí của những người được lấy mẫu từ chìa khóa. Để tính toán logits cho mỗi điểm dữ liệu cho mỗi mẫu sau, chúng ta có thể tăng gấp đôi vmap qua posterior_weights và features .

output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
    random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)

print('Average sample accuracy:', (
    output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
    output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())

Average sample accuracy: 0.9874067
BMA accuracy: 0.99333334

Sự kết luận

Trong Oryx, các chương trình xác suất chỉ là các hàm JAX lấy ngẫu nhiên (giả) làm đầu vào. Do sự tích hợp chặt chẽ của Oryx với hệ thống chuyển đổi chức năng của JAX, chúng tôi có thể viết và thao tác các chương trình xác suất giống như chúng tôi đang viết mã JAX. Điều này dẫn đến một hệ thống đơn giản nhưng linh hoạt để xây dựng các mô hình phức tạp và thực hiện suy luận.