Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Le bruit est présent dans les ordinateurs quantiques modernes. Qubits sont sensibles aux interférences de l'environnement, la fabrication imparfaite, TLS et parfois même des rayons gamma . Jusqu'à ce qu'une correction d'erreurs à grande échelle soit atteinte, les algorithmes d'aujourd'hui doivent pouvoir rester fonctionnels en présence de bruit. Cela fait du test d'algorithmes sous bruit une étape importante pour valider les algorithmes/modèles quantiques qui fonctionneront sur les ordinateurs quantiques d'aujourd'hui.
Dans ce tutoriel , vous découvrirez les bases de la simulation de circuit bruyant TFQ par le haut niveau tfq.layers API.
Installer
pip install tensorflow==2.4.1 tensorflow-quantum
pip install -q git+https://github.com/tensorflow/docs
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
import random
import cirq
import sympy
import tensorflow_quantum as tfq
import tensorflow as tf
import numpy as np
# Plotting
import matplotlib.pyplot as plt
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
2021-10-12 11:23:10.079578: E tensorflow/stream_executor/cuda/cuda_driver.cc:328] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Comprendre le bruit quantique
1.1 Bruit du circuit de base
Le bruit sur un ordinateur quantique a un impact sur les échantillons de chaînes de bits que vous pouvez mesurer à partir de celui-ci. Une façon intuitive de commencer à y penser est qu'un ordinateur quantique bruyant « insérera », « supprimera » ou « remplacera » des portes à des endroits aléatoires comme le diagramme ci-dessous :
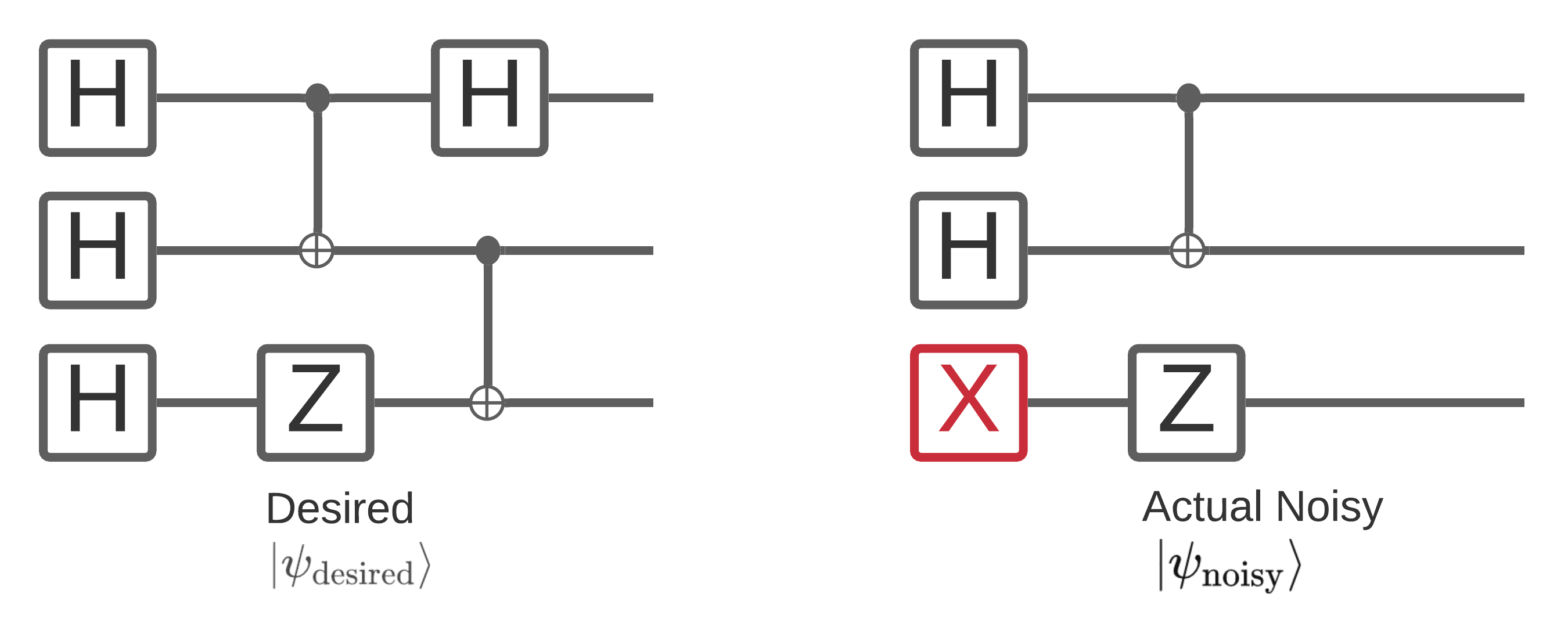
S'appuyant sur cette intuition, en traitant avec le bruit, vous n'utilisez un seul état pur \(|\psi \rangle\) , mais au lieu d'un traitement ensemble de toutes les réalisations possibles bruyantes de votre circuit souhaité: \(\rho = \sum_j p_j |\psi_j \rangle \langle \psi_j |\) . Où \(p_j\) donne la probabilité que le système est en \(|\psi_j \rangle\) .
En reprenant l'image ci-dessus, si nous savions à l'avance que 90% du temps notre système s'est parfaitement exécuté, ou s'est trompé 10% du temps avec ce seul mode de défaillance, alors notre ensemble serait :
\(\rho = 0.9 |\psi_\text{desired} \rangle \langle \psi_\text{desired}| + 0.1 |\psi_\text{noisy} \rangle \langle \psi_\text{noisy}| \)
S'il y avait plus d'une façon que notre circuit pourrait erreur, l'ensemble \(\rho\) contiendrait plus que deux termes (un pour chaque nouvelle réalisation bruyante qui pourrait se produire). \(\rho\) est appelée la matrice de densité décrivant votre système bruyant.
1.2 Utilisation de canaux pour modéliser le bruit de circuit
Malheureusement, dans la pratique, il est presque impossible de connaître toutes les erreurs possibles de votre circuit et leurs probabilités exactes. Une hypothèse simplificatrice que vous pouvez faire est que , après chaque opération dans votre circuit il y a une sorte de canal qui à peu près comment cette opération capture pourrait l' erreur. Vous pouvez rapidement créer un circuit avec du bruit :
def x_circuit(qubits):
"""Produces an X wall circuit on `qubits`."""
return cirq.Circuit(cirq.X.on_each(*qubits))
def make_noisy(circuit, p):
"""Add a depolarization channel to all qubits in `circuit` before measurement."""
return circuit + cirq.Circuit(cirq.depolarize(p).on_each(*circuit.all_qubits()))
my_qubits = cirq.GridQubit.rect(1, 2)
my_circuit = x_circuit(my_qubits)
my_noisy_circuit = make_noisy(my_circuit, 0.5)
my_circuit
my_noisy_circuit
Vous pouvez examiner la matrice de densité sans bruit \(\rho\) avec:
rho = cirq.final_density_matrix(my_circuit)
np.round(rho, 3)
array([[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 1.+0.j]], dtype=complex64)
Et la matrice de densité bruyante \(\rho\) avec:
rho = cirq.final_density_matrix(my_noisy_circuit)
np.round(rho, 3)
array([[0.111+0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0.222+0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0.222+0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0.444+0.j]], dtype=complex64)
En comparant les deux différents \( \rho \) « vous pouvez voir est que le bruit a eu un impact les amplitudes de l'état (et les probabilités d' échantillonnage en conséquence). Dans le cas sans bruit que vous attendez toujours goûter à la \( |11\rangle \) état. Mais dans l'état bruyant , il est maintenant une probabilité non nulle d'échantillonnage \( |00\rangle \) ou \( |01\rangle \) ou \( |10\rangle \) ainsi:
"""Sample from my_noisy_circuit."""
def plot_samples(circuit):
samples = cirq.sample(circuit + cirq.measure(*circuit.all_qubits(), key='bits'), repetitions=1000)
freqs, _ = np.histogram(samples.data['bits'], bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
plot_samples(my_noisy_circuit)
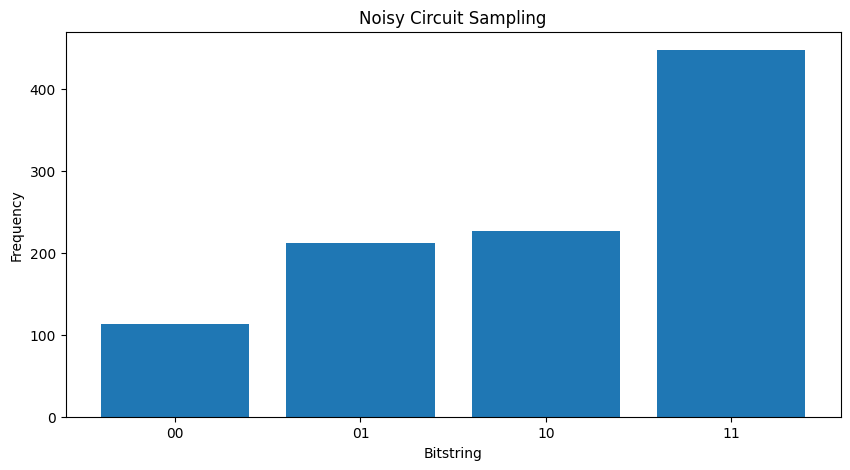
Sans bruit que vous obtiendrez toujours \(|11\rangle\):
"""Sample from my_circuit."""
plot_samples(my_circuit)
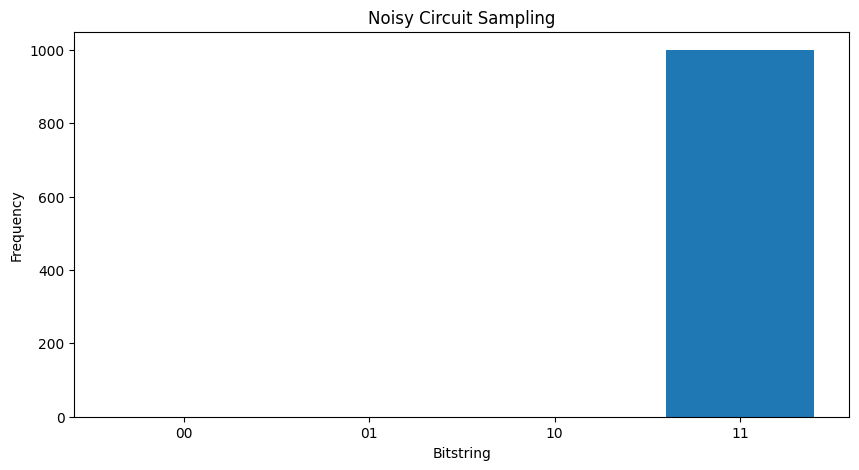
Si vous augmentez le bruit un peu plus loin , il deviendra de plus en plus difficile de distinguer le comportement souhaité (échantillonnage \(|11\rangle\) ) du bruit:
my_really_noisy_circuit = make_noisy(my_circuit, 0.75)
plot_samples(my_really_noisy_circuit)
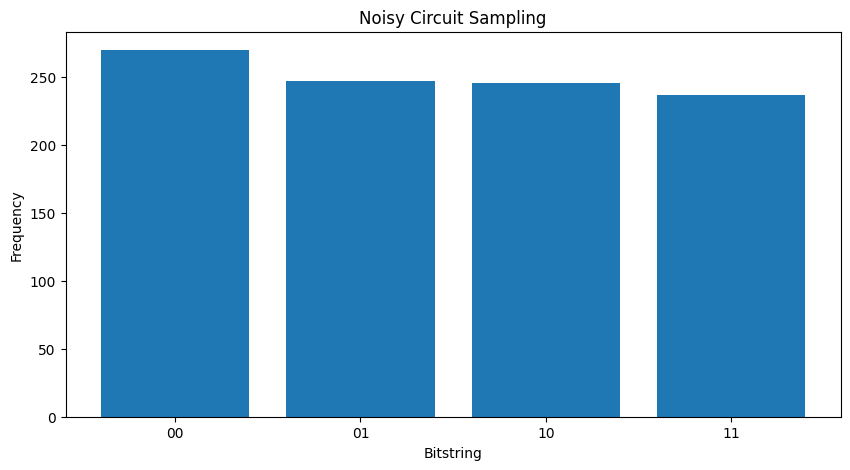
2. Bruit de base dans TFQ
Avec cette compréhension de l'impact du bruit sur l'exécution du circuit, vous pouvez explorer le fonctionnement du bruit dans TFQ. TensorFlow Quantum utilise la simulation basée sur monte-carlo/trajectoire comme alternative à la simulation matricielle de densité. En effet, la complexité de la mémoire de la simulation matricielle de densité limite les grandes simulations à <= 20 qubits avec les méthodes traditionnelles de simulation matricielle pleine densité. Monte-carlo / trajectoire troque ce coût en mémoire contre un surcoût dans le temps. Le backend='noisy' - tfq.layers.Sample tfq.layers.SampledExpectation tfq.layers.Expectation Expectation repetitions backend='noisy' option disponible pour tous tfq.layers.Sample , tfq.layers.SampledExpectation et tfq.layers.Expectation (Dans le cas d' Expectation cela n'ajoute une nécessaire repetitions paramètre).
2.1 Échantillonnage bruité dans TFQ
Pour recréer les parcelles ci - dessus à l' aide de la simulation et de la trajectoire TFQ vous pouvez utiliser tfq.layers.Sample
"""Draw bitstring samples from `my_noisy_circuit`"""
bitstrings = tfq.layers.Sample(backend='noisy')(my_noisy_circuit, repetitions=1000)
numeric_values = np.einsum('ijk,k->ij', bitstrings.to_tensor().numpy(), [1, 2])[0]
freqs, _ = np.histogram(numeric_values, bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
<BarContainer object of 4 artists>
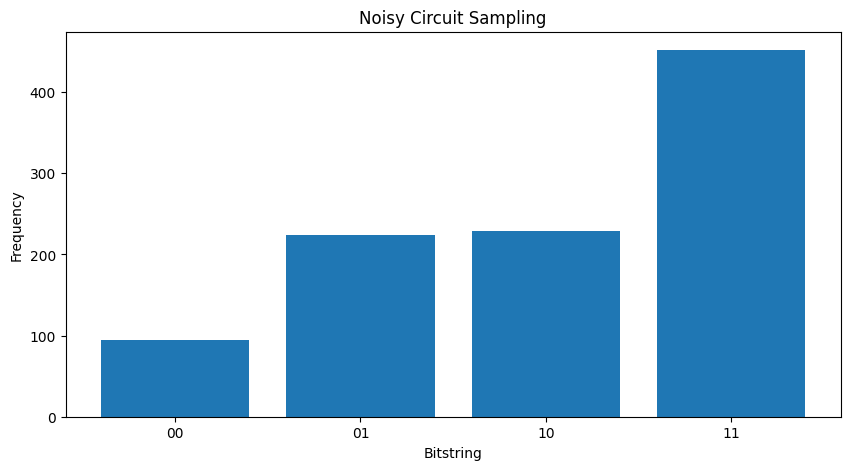
2.2 Attente basée sur un échantillon bruyant
Pour ce faire , le calcul de l' attente sur la base de l' échantillon bruyant , vous pouvez utiliser tfq.layers.SampleExpectation :
some_observables = [cirq.X(my_qubits[0]), cirq.Z(my_qubits[0]), 3.0 * cirq.Y(my_qubits[1]) + 1]
some_observables
[cirq.X(cirq.GridQubit(0, 0)),
cirq.Z(cirq.GridQubit(0, 0)),
cirq.PauliSum(cirq.LinearDict({frozenset({(cirq.GridQubit(0, 1), cirq.Y)}): (3+0j), frozenset(): (1+0j)}))]
Calculez les estimations d'attente sans bruit via l'échantillonnage du circuit :
noiseless_sampled_expectation = tfq.layers.SampledExpectation(backend='noiseless')(
my_circuit, operators=some_observables, repetitions=10000
)
noiseless_sampled_expectation.numpy()
array([[ 0.0076, -1. , 0.9796]], dtype=float32)
Comparez-les avec les versions bruyantes :
noisy_sampled_expectation = tfq.layers.SampledExpectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_sampled_expectation.numpy()
array([[ 0.0208 , -0.32099998, 1.0731999 ],
[-0.0126 , 0.0062 , 1.012 ]], dtype=float32)
Vous pouvez voir que le bruit a particulièrement impacté le \(\langle \psi | Z | \psi \rangle\) précision, avec my_really_noisy_circuit se concentrant très rapidement vers 0.
2.3 Calcul de l'espérance analytique bruyante
Faire des calculs d'attente analytique bruyants est presque identique à ci-dessus :
noiseless_analytic_expectation = tfq.layers.Expectation(backend='noiseless')(
my_circuit, operators=some_observables
)
noiseless_analytic_expectation.numpy()
array([[ 1.9106853e-15, -1.0000000e+00, 1.0000002e+00]], dtype=float32)
noisy_analytic_expectation = tfq.layers.Expectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_analytic_expectation.numpy()
array([[ 1.9106853e-15, -3.2819998e-01, 1.0000000e+00],
[ 1.9106855e-15, 1.3200002e-02, 1.0000000e+00]], dtype=float32)
3. Modèles hybrides et bruit de données quantiques
Maintenant que vous avez implémenté des simulations de circuits bruyants dans TFQ, vous pouvez expérimenter l'impact du bruit sur les modèles classiques quantiques et hybrides quantiques, en comparant et en contrastant leurs performances avec bruit et sans bruit. Une bonne première vérification pour voir si un modèle ou un algorithme est robuste au bruit consiste à tester sous un modèle de dépolarisation à l'échelle du circuit qui ressemble à ceci :
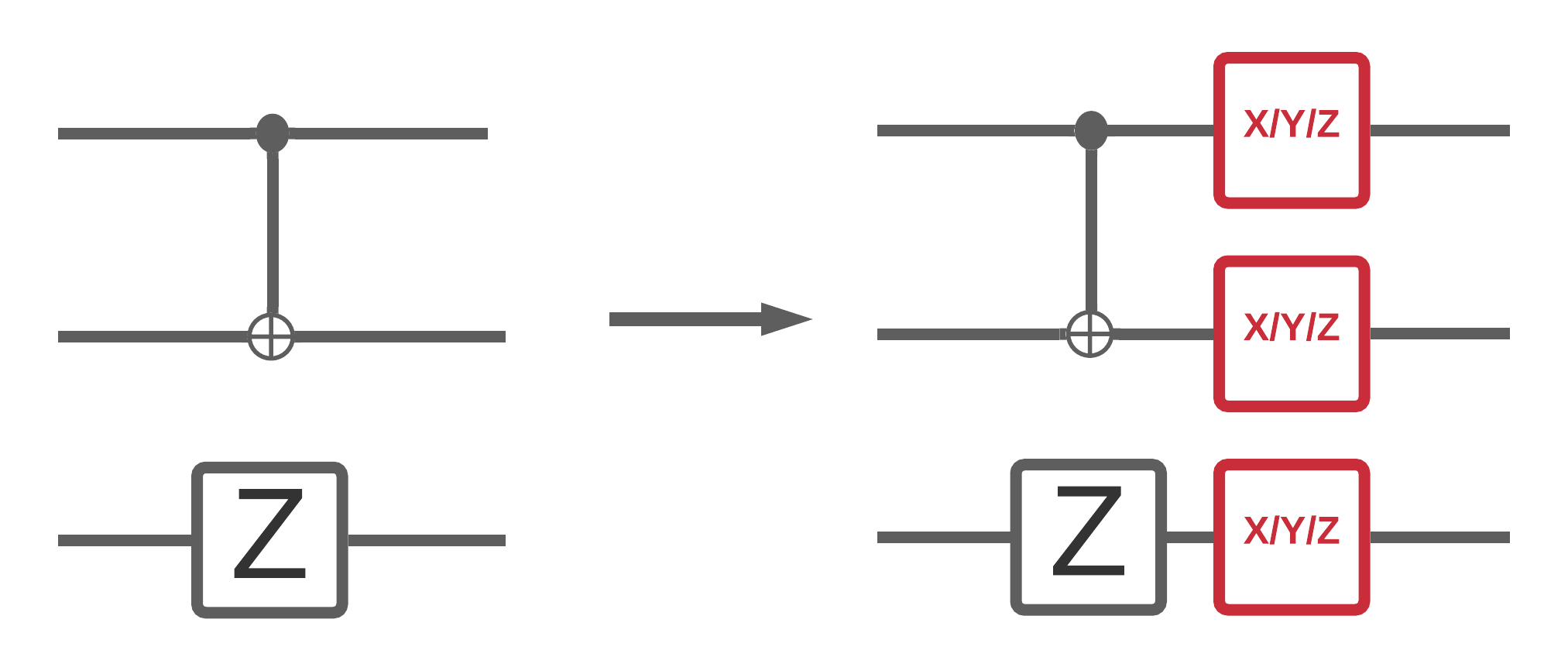
Où chaque tranche de temps du circuit (parfois appelée moment) a un canal de dépolarisation ajouté après chaque opération de porte dans cette tranche de temps. Le canal dépolarisants d'appliquer l' une des \(\{X, Y, Z \}\) avec une probabilité \(p\) ou appliquer rien (gardez l'opération d' origine) avec une probabilité \(1-p\).
3.1 Données
Pour cet exemple , vous pouvez utiliser des circuits préparés dans le tfq.datasets module comme données de formation:
qubits = cirq.GridQubit.rect(1, 8)
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
circuits[0]
Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/quantum/spin_systems/XXZ_chain.zip 184451072/184449737 [==============================] - 1s 0us/step
L'écriture d'une petite fonction d'assistance aidera à générer les données pour le cas bruyant vs sans bruit :
def get_data(qubits, depolarize_p=0.):
"""Return quantum data circuits and labels in `tf.Tensor` form."""
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
if depolarize_p >= 1e-5:
circuits = [circuit.with_noise(cirq.depolarize(depolarize_p)) for circuit in circuits]
tmp = list(zip(circuits, labels))
random.shuffle(tmp)
circuits_tensor = tfq.convert_to_tensor([x[0] for x in tmp])
labels_tensor = tf.convert_to_tensor([x[1] for x in tmp])
return circuits_tensor, labels_tensor
3.2 Définir un circuit modèle
Maintenant que vous avez des données quantiques sous forme de circuits, vous aurez besoin d'un circuit pour modéliser ces données, comme avec les données vous pouvez écrire une fonction d'assistance pour générer ce circuit contenant éventuellement du bruit :
def modelling_circuit(qubits, depth, depolarize_p=0.):
"""A simple classifier circuit."""
dim = len(qubits)
ret = cirq.Circuit(cirq.H.on_each(*qubits))
for i in range(depth):
# Entangle layer.
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[::2], qubits[1::2]))
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[1::2], qubits[2::2]))
# Learnable rotation layer.
# i_params = sympy.symbols(f'layer-{i}-0:{dim}')
param = sympy.Symbol(f'layer-{i}')
single_qb = cirq.X
if i % 2 == 1:
single_qb = cirq.Y
ret += cirq.Circuit(single_qb(q) ** param for q in qubits)
if depolarize_p >= 1e-5:
ret = ret.with_noise(cirq.depolarize(depolarize_p))
return ret, [op(q) for q in qubits for op in [cirq.X, cirq.Y, cirq.Z]]
modelling_circuit(qubits, 3)[0]
3.3 Construction de modèles et formation
Avec vos données et le circuit de modèle construit, la fonction d'assistance finale , vous aurez besoin est celui qui peut monter à la fois un bruit ou un hybride quantique sans bruit tf.keras.Model :
def build_keras_model(qubits, depolarize_p=0.):
"""Prepare a noisy hybrid quantum classical Keras model."""
spin_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
circuit_and_readout = modelling_circuit(qubits, 4, depolarize_p)
if depolarize_p >= 1e-5:
quantum_model = tfq.layers.NoisyPQC(*circuit_and_readout, sample_based=False, repetitions=10)(spin_input)
else:
quantum_model = tfq.layers.PQC(*circuit_and_readout)(spin_input)
intermediate = tf.keras.layers.Dense(4, activation='sigmoid')(quantum_model)
post_process = tf.keras.layers.Dense(1)(intermediate)
return tf.keras.Model(inputs=[spin_input], outputs=[post_process])
4. Comparez les performances
4.1 Ligne de base silencieuse
Avec votre génération de données et votre code de construction de modèle, vous pouvez maintenant comparer et contraster les performances du modèle dans les paramètres silencieux et bruyant, vous pouvez d'abord exécuter une formation sans bruit de référence :
training_histories = dict()
depolarize_p = 0.
n_epochs = 50
phase_classifier = build_keras_model(qubits, depolarize_p)
phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
# Show the keras plot of the model
tf.keras.utils.plot_model(phase_classifier, show_shapes=True, dpi=70)
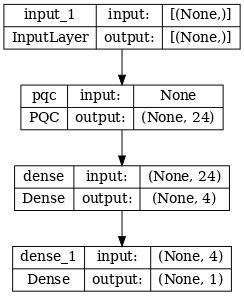
noiseless_data, noiseless_labels = get_data(qubits, depolarize_p)
training_histories['noiseless'] = phase_classifier.fit(x=noiseless_data,
y=noiseless_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 1s 218ms/step - loss: 0.7061 - accuracy: 0.5354 - val_loss: 0.6503 - val_accuracy: 0.6667 Epoch 2/50 4/4 [==============================] - 0s 86ms/step - loss: 0.6802 - accuracy: 0.5396 - val_loss: 0.6689 - val_accuracy: 0.6667 Epoch 3/50 4/4 [==============================] - 0s 83ms/step - loss: 0.6861 - accuracy: 0.4500 - val_loss: 0.6975 - val_accuracy: 0.6667 Epoch 4/50 4/4 [==============================] - 0s 82ms/step - loss: 0.6710 - accuracy: 0.4417 - val_loss: 0.7223 - val_accuracy: 0.6667 Epoch 5/50 4/4 [==============================] - 0s 82ms/step - loss: 0.6695 - accuracy: 0.4729 - val_loss: 0.7348 - val_accuracy: 0.6667 Epoch 6/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6526 - accuracy: 0.6146 - val_loss: 0.7379 - val_accuracy: 0.9167 Epoch 7/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6480 - accuracy: 0.7875 - val_loss: 0.7291 - val_accuracy: 1.0000 Epoch 8/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6365 - accuracy: 0.7771 - val_loss: 0.7116 - val_accuracy: 1.0000 Epoch 9/50 4/4 [==============================] - 0s 78ms/step - loss: 0.6311 - accuracy: 0.7521 - val_loss: 0.6915 - val_accuracy: 0.9167 Epoch 10/50 4/4 [==============================] - 0s 79ms/step - loss: 0.6081 - accuracy: 0.7000 - val_loss: 0.6706 - val_accuracy: 0.9167 Epoch 11/50 4/4 [==============================] - 0s 86ms/step - loss: 0.6163 - accuracy: 0.6771 - val_loss: 0.6395 - val_accuracy: 0.8333 Epoch 12/50 4/4 [==============================] - 0s 83ms/step - loss: 0.5897 - accuracy: 0.6500 - val_loss: 0.6194 - val_accuracy: 0.8333 Epoch 13/50 4/4 [==============================] - 1s 148ms/step - loss: 0.5791 - accuracy: 0.6708 - val_loss: 0.6012 - val_accuracy: 0.9167 Epoch 14/50 4/4 [==============================] - 0s 83ms/step - loss: 0.5650 - accuracy: 0.6396 - val_loss: 0.5838 - val_accuracy: 0.9167 Epoch 15/50 4/4 [==============================] - 0s 87ms/step - loss: 0.5702 - accuracy: 0.7167 - val_loss: 0.5576 - val_accuracy: 0.9167 Epoch 16/50 4/4 [==============================] - 0s 89ms/step - loss: 0.5475 - accuracy: 0.6750 - val_loss: 0.5391 - val_accuracy: 1.0000 Epoch 17/50 4/4 [==============================] - 0s 84ms/step - loss: 0.5346 - accuracy: 0.7146 - val_loss: 0.5167 - val_accuracy: 1.0000 Epoch 18/50 4/4 [==============================] - 0s 92ms/step - loss: 0.5329 - accuracy: 0.7812 - val_loss: 0.4905 - val_accuracy: 1.0000 Epoch 19/50 4/4 [==============================] - 0s 90ms/step - loss: 0.4863 - accuracy: 0.7708 - val_loss: 0.4731 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 0s 88ms/step - loss: 0.4724 - accuracy: 0.7875 - val_loss: 0.4549 - val_accuracy: 1.0000 Epoch 21/50 4/4 [==============================] - 0s 94ms/step - loss: 0.4780 - accuracy: 0.8396 - val_loss: 0.4301 - val_accuracy: 1.0000 Epoch 22/50 4/4 [==============================] - 0s 85ms/step - loss: 0.4446 - accuracy: 0.8375 - val_loss: 0.4101 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 0s 92ms/step - loss: 0.4458 - accuracy: 0.8396 - val_loss: 0.3863 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 0s 93ms/step - loss: 0.4097 - accuracy: 0.8750 - val_loss: 0.3616 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 0s 89ms/step - loss: 0.3907 - accuracy: 0.8750 - val_loss: 0.3410 - val_accuracy: 1.0000 Epoch 26/50 4/4 [==============================] - 0s 91ms/step - loss: 0.3842 - accuracy: 0.8646 - val_loss: 0.3180 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 0s 90ms/step - loss: 0.3509 - accuracy: 0.9062 - val_loss: 0.2951 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 0s 91ms/step - loss: 0.3495 - accuracy: 0.8688 - val_loss: 0.2813 - val_accuracy: 1.0000 Epoch 29/50 4/4 [==============================] - 0s 94ms/step - loss: 0.3393 - accuracy: 0.8917 - val_loss: 0.2606 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 0s 92ms/step - loss: 0.3277 - accuracy: 0.8750 - val_loss: 0.2449 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 0s 90ms/step - loss: 0.2935 - accuracy: 0.9292 - val_loss: 0.2331 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 0s 91ms/step - loss: 0.2875 - accuracy: 0.9229 - val_loss: 0.2188 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 0s 94ms/step - loss: 0.2820 - accuracy: 0.9354 - val_loss: 0.2049 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 0s 93ms/step - loss: 0.2705 - accuracy: 0.8958 - val_loss: 0.1957 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 0s 91ms/step - loss: 0.2499 - accuracy: 0.9500 - val_loss: 0.1832 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 0s 92ms/step - loss: 0.2445 - accuracy: 0.9354 - val_loss: 0.1705 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 0s 90ms/step - loss: 0.2533 - accuracy: 0.9437 - val_loss: 0.1623 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 0s 96ms/step - loss: 0.2253 - accuracy: 0.9542 - val_loss: 0.1525 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 0s 89ms/step - loss: 0.2189 - accuracy: 0.9646 - val_loss: 0.1425 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 0s 95ms/step - loss: 0.2273 - accuracy: 0.9417 - val_loss: 0.1372 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 0s 85ms/step - loss: 0.2346 - accuracy: 0.9437 - val_loss: 0.1325 - val_accuracy: 1.0000 Epoch 42/50 4/4 [==============================] - 0s 96ms/step - loss: 0.2227 - accuracy: 0.9479 - val_loss: 0.1235 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 1s 149ms/step - loss: 0.2134 - accuracy: 0.9437 - val_loss: 0.1192 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 0s 85ms/step - loss: 0.2066 - accuracy: 0.9250 - val_loss: 0.1149 - val_accuracy: 1.0000 Epoch 45/50 4/4 [==============================] - 0s 83ms/step - loss: 0.2168 - accuracy: 0.9375 - val_loss: 0.1095 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 0s 84ms/step - loss: 0.1759 - accuracy: 0.9604 - val_loss: 0.1053 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 0s 81ms/step - loss: 0.1850 - accuracy: 0.9833 - val_loss: 0.0980 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 0s 81ms/step - loss: 0.1910 - accuracy: 0.9479 - val_loss: 0.0913 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 0s 80ms/step - loss: 0.1698 - accuracy: 0.9250 - val_loss: 0.0911 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 0s 83ms/step - loss: 0.1698 - accuracy: 0.9542 - val_loss: 0.0855 - val_accuracy: 1.0000
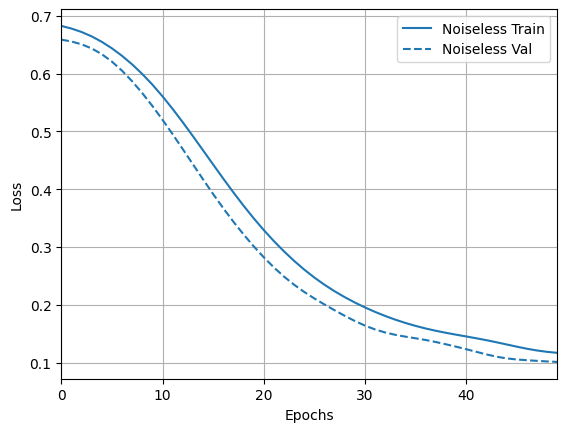
Et explorez les résultats et la précision :
loss_plotter = tfdocs.plots.HistoryPlotter(metric = 'loss', smoothing_std=10)
loss_plotter.plot(training_histories)
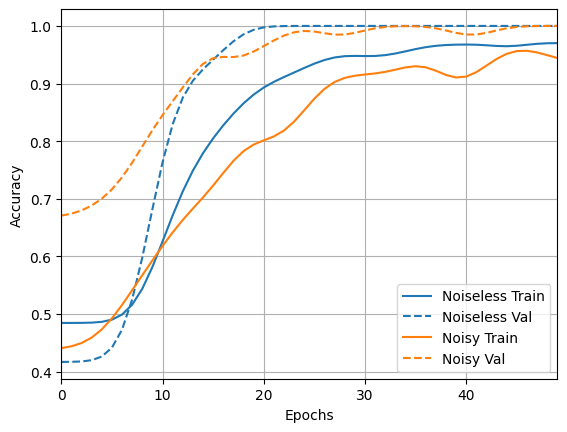
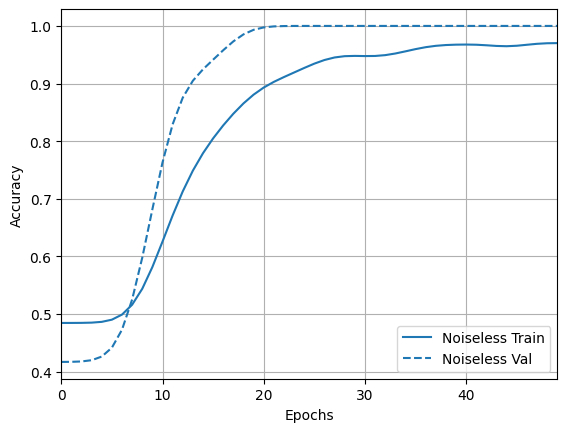
acc_plotter = tfdocs.plots.HistoryPlotter(metric = 'accuracy', smoothing_std=10)
acc_plotter.plot(training_histories)
4.2 Comparaison du bruit
Vous pouvez maintenant créer un nouveau modèle avec une structure bruyante et comparer à ce qui précède, le code est presque identique :
depolarize_p = 0.001
n_epochs = 50
noisy_phase_classifier = build_keras_model(qubits, depolarize_p)
noisy_phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
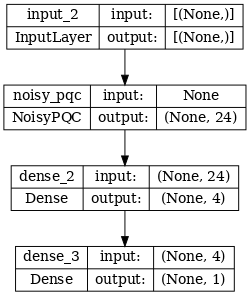
# Show the keras plot of the model
tf.keras.utils.plot_model(noisy_phase_classifier, show_shapes=True, dpi=70)
noisy_data, noisy_labels = get_data(qubits, depolarize_p)
training_histories['noisy'] = noisy_phase_classifier.fit(x=noisy_data,
y=noisy_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 8s 2s/step - loss: 0.6710 - accuracy: 0.3771 - val_loss: 0.8007 - val_accuracy: 0.7500 Epoch 2/50 4/4 [==============================] - 7s 2s/step - loss: 0.6745 - accuracy: 0.4271 - val_loss: 0.7787 - val_accuracy: 0.7500 Epoch 3/50 4/4 [==============================] - 7s 2s/step - loss: 0.6698 - accuracy: 0.4354 - val_loss: 0.7603 - val_accuracy: 0.7500 Epoch 4/50 4/4 [==============================] - 7s 2s/step - loss: 0.6528 - accuracy: 0.4083 - val_loss: 0.7550 - val_accuracy: 0.7500 Epoch 5/50 4/4 [==============================] - 7s 2s/step - loss: 0.6535 - accuracy: 0.4313 - val_loss: 0.7370 - val_accuracy: 0.8333 Epoch 6/50 4/4 [==============================] - 7s 2s/step - loss: 0.6445 - accuracy: 0.4979 - val_loss: 0.7201 - val_accuracy: 0.8333 Epoch 7/50 4/4 [==============================] - 7s 2s/step - loss: 0.6333 - accuracy: 0.4917 - val_loss: 0.7185 - val_accuracy: 0.8333 Epoch 8/50 4/4 [==============================] - 7s 2s/step - loss: 0.6152 - accuracy: 0.5854 - val_loss: 0.6988 - val_accuracy: 0.9167 Epoch 9/50 4/4 [==============================] - 7s 2s/step - loss: 0.5806 - accuracy: 0.6562 - val_loss: 0.6805 - val_accuracy: 0.9167 Epoch 10/50 4/4 [==============================] - 7s 2s/step - loss: 0.5872 - accuracy: 0.6854 - val_loss: 0.6599 - val_accuracy: 0.9167 Epoch 11/50 4/4 [==============================] - 7s 2s/step - loss: 0.5753 - accuracy: 0.7875 - val_loss: 0.6401 - val_accuracy: 0.9167 Epoch 12/50 4/4 [==============================] - 7s 2s/step - loss: 0.5682 - accuracy: 0.8354 - val_loss: 0.6097 - val_accuracy: 0.9167 Epoch 13/50 4/4 [==============================] - 7s 2s/step - loss: 0.5380 - accuracy: 0.8396 - val_loss: 0.5732 - val_accuracy: 0.9167 Epoch 14/50 4/4 [==============================] - 7s 2s/step - loss: 0.5061 - accuracy: 0.7708 - val_loss: 0.5657 - val_accuracy: 0.9167 Epoch 15/50 4/4 [==============================] - 7s 2s/step - loss: 0.5043 - accuracy: 0.8604 - val_loss: 0.5254 - val_accuracy: 1.0000 Epoch 16/50 4/4 [==============================] - 7s 2s/step - loss: 0.4795 - accuracy: 0.8708 - val_loss: 0.4805 - val_accuracy: 1.0000 Epoch 17/50 4/4 [==============================] - 7s 2s/step - loss: 0.4456 - accuracy: 0.8000 - val_loss: 0.4539 - val_accuracy: 1.0000 Epoch 18/50 4/4 [==============================] - 7s 2s/step - loss: 0.4512 - accuracy: 0.9021 - val_loss: 0.4331 - val_accuracy: 1.0000 Epoch 19/50 4/4 [==============================] - 7s 2s/step - loss: 0.4210 - accuracy: 0.8688 - val_loss: 0.4411 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 7s 2s/step - loss: 0.4167 - accuracy: 0.8646 - val_loss: 0.3781 - val_accuracy: 0.9167 Epoch 21/50 4/4 [==============================] - 7s 2s/step - loss: 0.3550 - accuracy: 0.9375 - val_loss: 0.3492 - val_accuracy: 1.0000 Epoch 22/50 4/4 [==============================] - 7s 2s/step - loss: 0.3720 - accuracy: 0.9000 - val_loss: 0.3550 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 7s 2s/step - loss: 0.3251 - accuracy: 0.9292 - val_loss: 0.3234 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 7s 2s/step - loss: 0.3264 - accuracy: 0.9333 - val_loss: 0.2942 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 7s 2s/step - loss: 0.2937 - accuracy: 0.9125 - val_loss: 0.3439 - val_accuracy: 0.9167 Epoch 26/50 4/4 [==============================] - 7s 2s/step - loss: 0.2798 - accuracy: 0.9250 - val_loss: 0.2842 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 7s 2s/step - loss: 0.2835 - accuracy: 0.9479 - val_loss: 0.2385 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 7s 2s/step - loss: 0.2610 - accuracy: 0.9417 - val_loss: 0.2352 - val_accuracy: 1.0000 Epoch 29/50 4/4 [==============================] - 7s 2s/step - loss: 0.2916 - accuracy: 0.8875 - val_loss: 0.2221 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 7s 2s/step - loss: 0.2620 - accuracy: 0.9417 - val_loss: 0.2054 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 7s 2s/step - loss: 0.2015 - accuracy: 0.9417 - val_loss: 0.2074 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 7s 2s/step - loss: 0.2462 - accuracy: 0.9292 - val_loss: 0.1961 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 7s 2s/step - loss: 0.2042 - accuracy: 0.9938 - val_loss: 0.1820 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 7s 2s/step - loss: 0.1951 - accuracy: 0.9667 - val_loss: 0.1748 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 7s 2s/step - loss: 0.2175 - accuracy: 0.9271 - val_loss: 0.1628 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 7s 2s/step - loss: 0.1792 - accuracy: 0.9563 - val_loss: 0.1569 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 7s 2s/step - loss: 0.1809 - accuracy: 0.9229 - val_loss: 0.1613 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 7s 2s/step - loss: 0.1747 - accuracy: 0.9313 - val_loss: 0.1622 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 7s 2s/step - loss: 0.1588 - accuracy: 1.0000 - val_loss: 0.1483 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 7s 2s/step - loss: 0.1709 - accuracy: 0.9437 - val_loss: 0.1428 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 7s 2s/step - loss: 0.1743 - accuracy: 0.9563 - val_loss: 0.1420 - val_accuracy: 0.9167 Epoch 42/50 4/4 [==============================] - 7s 2s/step - loss: 0.2167 - accuracy: 0.9021 - val_loss: 0.1526 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 7s 2s/step - loss: 0.1694 - accuracy: 0.9271 - val_loss: 0.1315 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 7s 2s/step - loss: 0.1597 - accuracy: 0.9646 - val_loss: 0.1601 - val_accuracy: 0.9167 Epoch 45/50 4/4 [==============================] - 7s 2s/step - loss: 0.1764 - accuracy: 0.9437 - val_loss: 0.1094 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 7s 2s/step - loss: 0.1582 - accuracy: 0.9542 - val_loss: 0.1403 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 7s 2s/step - loss: 0.1879 - accuracy: 0.9542 - val_loss: 0.0674 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 7s 2s/step - loss: 0.1812 - accuracy: 0.9708 - val_loss: 0.0751 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 7s 2s/step - loss: 0.1231 - accuracy: 0.9875 - val_loss: 0.1512 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 7s 2s/step - loss: 0.1537 - accuracy: 0.9292 - val_loss: 0.0958 - val_accuracy: 1.0000
loss_plotter.plot(training_histories)
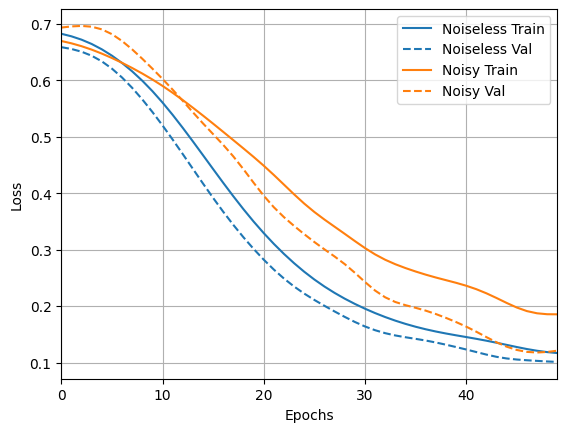
acc_plotter.plot(training_histories)