 TensorFlow.org에서 보기 TensorFlow.org에서 보기 |  Google Colab에서 실행 Google Colab에서 실행 |  GitHub에서 소스 보기 GitHub에서 소스 보기 |  노트북 다운로드 노트북 다운로드 |
이 튜토리얼은 변환적으로 불변 인 고전적인 길쌈 신경망에 대한 제안된 양자 유사체인 단순화된 양자 길쌈 신경망 (QCNN)을 구현합니다.
이 예는 양자 센서 또는 장치의 복잡한 시뮬레이션과 같은 양자 데이터 소스의 특정 속성을 감지하는 방법을 보여줍니다. 양자 데이터 소스는 여기가 있을 수도 있고 없을 수도 있는 클러스터 상태 이며 QCNN이 감지하는 방법을 학습합니다(논문에서 사용된 데이터 세트는 SPT 위상 분류였습니다).
설정
pip install tensorflow==2.7.0
TensorFlow Quantum 설치:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
이제 TensorFlow 및 모듈 종속성을 가져옵니다.
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:43:45.380301: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. QCNN 구축
1.1 TensorFlow 그래프에서 회로 조립
TensorFlow Quantum(TFQ)은 그래프 내 회로 구성을 위해 설계된 계층 클래스를 제공합니다. 한 가지 예는 tf.keras.Layer 에서 상속되는 tfq.layers.AddCircuit 레이어입니다. 이 레이어는 다음 그림과 같이 회로의 입력 배치 앞에 추가하거나 추가할 수 있습니다.

다음 스니펫은 이 레이어를 사용합니다.
qubit = cirq.GridQubit(0, 0)
# Define some circuits.
circuit1 = cirq.Circuit(cirq.X(qubit))
circuit2 = cirq.Circuit(cirq.H(qubit))
# Convert to a tensor.
input_circuit_tensor = tfq.convert_to_tensor([circuit1, circuit2])
# Define a circuit that we want to append
y_circuit = cirq.Circuit(cirq.Y(qubit))
# Instantiate our layer
y_appender = tfq.layers.AddCircuit()
# Run our circuit tensor through the layer and save the output.
output_circuit_tensor = y_appender(input_circuit_tensor, append=y_circuit)
입력 텐서를 검사합니다.
print(tfq.from_tensor(input_circuit_tensor))
[cirq.Circuit([
cirq.Moment(
cirq.X(cirq.GridQubit(0, 0)),
),
])
cirq.Circuit([
cirq.Moment(
cirq.H(cirq.GridQubit(0, 0)),
),
]) ]
그리고 출력 텐서를 검사합니다.
print(tfq.from_tensor(output_circuit_tensor))
[cirq.Circuit([
cirq.Moment(
cirq.X(cirq.GridQubit(0, 0)),
),
cirq.Moment(
cirq.Y(cirq.GridQubit(0, 0)),
),
])
cirq.Circuit([
cirq.Moment(
cirq.H(cirq.GridQubit(0, 0)),
),
cirq.Moment(
cirq.Y(cirq.GridQubit(0, 0)),
),
]) ]
tfq.layers.AddCircuit 를 사용하지 않고 아래 예제를 실행할 수 있지만 TensorFlow 컴퓨팅 그래프에 복잡한 기능을 포함할 수 있는 방법을 이해할 수 있는 좋은 기회입니다.
1.2 문제 개요
클러스터 상태 를 준비하고 양자 분류기를 훈련하여 "흥분된" 상태인지 여부를 감지합니다. 클러스터 상태는 복잡하게 얽혀 있지만 고전적인 컴퓨터에서 반드시 어려운 것은 아닙니다. 명확성을 위해 이것은 논문에서 사용된 것보다 간단한 데이터 세트입니다.
이 분류 작업을 위해 다음과 같은 이유로 깊은 MERA 와 같은 QCNN 아키텍처를 구현합니다.
- QCNN과 마찬가지로 링의 클러스터 상태는 변환적으로 불변입니다.
- 클러스터 상태가 심하게 얽혀 있습니다.
이 아키텍처는 얽힘을 줄이는 데 효과적이어야 하며 단일 큐비트를 읽어서 분류를 얻습니다.

"흥분된" 클러스터 상태는 큐비트에 cirq.rx 게이트가 적용된 클러스터 상태로 정의됩니다. Qconv 및 QPool은 이 자습서의 뒷부분에서 설명합니다.
1.3 TensorFlow를 위한 빌딩 블록

TensorFlow Quantum으로 이 문제를 해결하는 한 가지 방법은 다음을 구현하는 것입니다.
- 모델에 대한 입력은 빈 회로 또는 여기를 나타내는 특정 큐비트의 X 게이트인 회로 텐서입니다.
- 모델의 나머지 양자 구성 요소는
tfq.layers.AddCircuit레이어로 구성됩니다. - 추론을 위해
tfq.layers.PQC레이어가 사용됩니다. 이것은 \(\langle \hat{Z} \rangle\) 을 읽고 들뜬 상태의 경우 레이블 1과 비교하거나 비 여기 상태의 경우 -1과 비교합니다.
1.4 데이터
모델을 구축하기 전에 데이터를 생성할 수 있습니다. 이 경우 클러스터 상태에 대한 여기가 될 것입니다(원본 논문은 더 복잡한 데이터 세트를 사용함). 가진은 cirq.rx 게이트로 표시됩니다. 충분히 큰 회전은 여기로 간주되어 1 로 표시되고 충분히 크지 않은 회전은 -1 로 표시되어 여기가 아닌 것으로 간주됩니다.
def generate_data(qubits):
"""Generate training and testing data."""
n_rounds = 20 # Produces n_rounds * n_qubits datapoints.
excitations = []
labels = []
for n in range(n_rounds):
for bit in qubits:
rng = np.random.uniform(-np.pi, np.pi)
excitations.append(cirq.Circuit(cirq.rx(rng)(bit)))
labels.append(1 if (-np.pi / 2) <= rng <= (np.pi / 2) else -1)
split_ind = int(len(excitations) * 0.7)
train_excitations = excitations[:split_ind]
test_excitations = excitations[split_ind:]
train_labels = labels[:split_ind]
test_labels = labels[split_ind:]
return tfq.convert_to_tensor(train_excitations), np.array(train_labels), \
tfq.convert_to_tensor(test_excitations), np.array(test_labels)
일반 기계 학습과 마찬가지로 모델을 벤치마킹하는 데 사용할 훈련 및 테스트 세트를 생성하는 것을 볼 수 있습니다. 다음을 사용하여 일부 데이터 포인트를 빠르게 볼 수 있습니다.
sample_points, sample_labels, _, __ = generate_data(cirq.GridQubit.rect(1, 4))
print('Input:', tfq.from_tensor(sample_points)[0], 'Output:', sample_labels[0])
print('Input:', tfq.from_tensor(sample_points)[1], 'Output:', sample_labels[1])
Input: (0, 0): ───X^0.449─── Output: 1 Input: (0, 1): ───X^-0.74─── Output: -1
1.5 레이어 정의
이제 TensorFlow에서 위 그림에 표시된 레이어를 정의합니다.
1.5.1 클러스터 상태
첫 번째 단계는 양자 회로 프로그래밍을 위해 Google에서 제공하는 프레임워크인 Cirq 를 사용하여 클러스터 상태 를 정의하는 것입니다. 이것은 모델의 정적 부분 tfq.layers.AddCircuit 기능을 사용하여 포함합니다.
def cluster_state_circuit(bits):
"""Return a cluster state on the qubits in `bits`."""
circuit = cirq.Circuit()
circuit.append(cirq.H.on_each(bits))
for this_bit, next_bit in zip(bits, bits[1:] + [bits[0]]):
circuit.append(cirq.CZ(this_bit, next_bit))
return circuit
cirq.GridQubit 의 직사각형에 대한 클러스터 상태 회로를 표시합니다.
SVGCircuit(cluster_state_circuit(cirq.GridQubit.rect(1, 4)))
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
1.5.2 QCNN 계층
Cong 및 Lukin QCNN 페이퍼 를 사용하여 모델을 구성하는 레이어를 정의합니다. 몇 가지 전제 조건이 있습니다.
- Tucci 논문 에서 1 및 2 큐비트 매개변수화된 단일 행렬.
- 일반적인 매개변수화된 2큐비트 풀링 작업입니다.
def one_qubit_unitary(bit, symbols):
"""Make a Cirq circuit enacting a rotation of the bloch sphere about the X,
Y and Z axis, that depends on the values in `symbols`.
"""
return cirq.Circuit(
cirq.X(bit)**symbols[0],
cirq.Y(bit)**symbols[1],
cirq.Z(bit)**symbols[2])
def two_qubit_unitary(bits, symbols):
"""Make a Cirq circuit that creates an arbitrary two qubit unitary."""
circuit = cirq.Circuit()
circuit += one_qubit_unitary(bits[0], symbols[0:3])
circuit += one_qubit_unitary(bits[1], symbols[3:6])
circuit += [cirq.ZZ(*bits)**symbols[6]]
circuit += [cirq.YY(*bits)**symbols[7]]
circuit += [cirq.XX(*bits)**symbols[8]]
circuit += one_qubit_unitary(bits[0], symbols[9:12])
circuit += one_qubit_unitary(bits[1], symbols[12:])
return circuit
def two_qubit_pool(source_qubit, sink_qubit, symbols):
"""Make a Cirq circuit to do a parameterized 'pooling' operation, which
attempts to reduce entanglement down from two qubits to just one."""
pool_circuit = cirq.Circuit()
sink_basis_selector = one_qubit_unitary(sink_qubit, symbols[0:3])
source_basis_selector = one_qubit_unitary(source_qubit, symbols[3:6])
pool_circuit.append(sink_basis_selector)
pool_circuit.append(source_basis_selector)
pool_circuit.append(cirq.CNOT(control=source_qubit, target=sink_qubit))
pool_circuit.append(sink_basis_selector**-1)
return pool_circuit
생성한 것을 보려면 1큐비트 단일 회로를 인쇄하십시오.
SVGCircuit(one_qubit_unitary(cirq.GridQubit(0, 0), sympy.symbols('x0:3')))
그리고 2-큐비트 단일 회로:
SVGCircuit(two_qubit_unitary(cirq.GridQubit.rect(1, 2), sympy.symbols('x0:15')))
그리고 2큐비트 풀링 회로:
SVGCircuit(two_qubit_pool(*cirq.GridQubit.rect(1, 2), sympy.symbols('x0:6')))
1.5.2.1 양자 컨볼루션
Cong 및 Lukin 논문에서와 같이 1D 양자 컨볼루션을 1의 보폭으로 인접한 큐비트의 모든 쌍에 2-큐비트 매개변수화된 단일체를 적용하는 것으로 정의합니다.
def quantum_conv_circuit(bits, symbols):
"""Quantum Convolution Layer following the above diagram.
Return a Cirq circuit with the cascade of `two_qubit_unitary` applied
to all pairs of qubits in `bits` as in the diagram above.
"""
circuit = cirq.Circuit()
for first, second in zip(bits[0::2], bits[1::2]):
circuit += two_qubit_unitary([first, second], symbols)
for first, second in zip(bits[1::2], bits[2::2] + [bits[0]]):
circuit += two_qubit_unitary([first, second], symbols)
return circuit
(매우 수평적인) 회로 표시:
SVGCircuit(
quantum_conv_circuit(cirq.GridQubit.rect(1, 8), sympy.symbols('x0:15')))
1.5.2.2 양자 풀링
양자 풀링 레이어는 위에 정의된 2큐비트 풀을 사용하여 \(\frac{N}{2}\) \(N\) 비트에서 l10n-placeholder3 큐비트로 풀링됩니다.
def quantum_pool_circuit(source_bits, sink_bits, symbols):
"""A layer that specifies a quantum pooling operation.
A Quantum pool tries to learn to pool the relevant information from two
qubits onto 1.
"""
circuit = cirq.Circuit()
for source, sink in zip(source_bits, sink_bits):
circuit += two_qubit_pool(source, sink, symbols)
return circuit
풀링 구성 요소 회로를 검사합니다.
test_bits = cirq.GridQubit.rect(1, 8)
SVGCircuit(
quantum_pool_circuit(test_bits[:4], test_bits[4:], sympy.symbols('x0:6')))
1.6 모델 정의
이제 정의된 레이어를 사용하여 순수한 양자 CNN을 구성합니다. 8개의 큐비트로 시작하여 1개로 풀링한 다음 \(\langle \hat{Z} \rangle\)를 측정합니다.
def create_model_circuit(qubits):
"""Create sequence of alternating convolution and pooling operators
which gradually shrink over time."""
model_circuit = cirq.Circuit()
symbols = sympy.symbols('qconv0:63')
# Cirq uses sympy.Symbols to map learnable variables. TensorFlow Quantum
# scans incoming circuits and replaces these with TensorFlow variables.
model_circuit += quantum_conv_circuit(qubits, symbols[0:15])
model_circuit += quantum_pool_circuit(qubits[:4], qubits[4:],
symbols[15:21])
model_circuit += quantum_conv_circuit(qubits[4:], symbols[21:36])
model_circuit += quantum_pool_circuit(qubits[4:6], qubits[6:],
symbols[36:42])
model_circuit += quantum_conv_circuit(qubits[6:], symbols[42:57])
model_circuit += quantum_pool_circuit([qubits[6]], [qubits[7]],
symbols[57:63])
return model_circuit
# Create our qubits and readout operators in Cirq.
cluster_state_bits = cirq.GridQubit.rect(1, 8)
readout_operators = cirq.Z(cluster_state_bits[-1])
# Build a sequential model enacting the logic in 1.3 of this notebook.
# Here you are making the static cluster state prep as a part of the AddCircuit and the
# "quantum datapoints" are coming in the form of excitation
excitation_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
cluster_state = tfq.layers.AddCircuit()(
excitation_input, prepend=cluster_state_circuit(cluster_state_bits))
quantum_model = tfq.layers.PQC(create_model_circuit(cluster_state_bits),
readout_operators)(cluster_state)
qcnn_model = tf.keras.Model(inputs=[excitation_input], outputs=[quantum_model])
# Show the keras plot of the model
tf.keras.utils.plot_model(qcnn_model,
show_shapes=True,
show_layer_names=False,
dpi=70)

1.7 모델 훈련
이 예제를 단순화하기 위해 전체 배치에 대해 모델을 훈련시키십시오.
# Generate some training data.
train_excitations, train_labels, test_excitations, test_labels = generate_data(
cluster_state_bits)
# Custom accuracy metric.
@tf.function
def custom_accuracy(y_true, y_pred):
y_true = tf.squeeze(y_true)
y_pred = tf.map_fn(lambda x: 1.0 if x >= 0 else -1.0, y_pred)
return tf.keras.backend.mean(tf.keras.backend.equal(y_true, y_pred))
qcnn_model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.losses.mse,
metrics=[custom_accuracy])
history = qcnn_model.fit(x=train_excitations,
y=train_labels,
batch_size=16,
epochs=25,
verbose=1,
validation_data=(test_excitations, test_labels))
Epoch 1/25 7/7 [==============================] - 2s 176ms/step - loss: 0.8961 - custom_accuracy: 0.7143 - val_loss: 0.8012 - val_custom_accuracy: 0.7500 Epoch 2/25 7/7 [==============================] - 1s 140ms/step - loss: 0.7736 - custom_accuracy: 0.7946 - val_loss: 0.7355 - val_custom_accuracy: 0.8542 Epoch 3/25 7/7 [==============================] - 1s 138ms/step - loss: 0.7319 - custom_accuracy: 0.8393 - val_loss: 0.7045 - val_custom_accuracy: 0.8125 Epoch 4/25 7/7 [==============================] - 1s 137ms/step - loss: 0.6976 - custom_accuracy: 0.8482 - val_loss: 0.6829 - val_custom_accuracy: 0.8333 Epoch 5/25 7/7 [==============================] - 1s 143ms/step - loss: 0.6696 - custom_accuracy: 0.8750 - val_loss: 0.6749 - val_custom_accuracy: 0.7917 Epoch 6/25 7/7 [==============================] - 1s 137ms/step - loss: 0.6631 - custom_accuracy: 0.8750 - val_loss: 0.6718 - val_custom_accuracy: 0.7917 Epoch 7/25 7/7 [==============================] - 1s 135ms/step - loss: 0.6536 - custom_accuracy: 0.8929 - val_loss: 0.6638 - val_custom_accuracy: 0.8750 Epoch 8/25 7/7 [==============================] - 1s 141ms/step - loss: 0.6376 - custom_accuracy: 0.8750 - val_loss: 0.6311 - val_custom_accuracy: 0.8542 Epoch 9/25 7/7 [==============================] - 1s 137ms/step - loss: 0.6208 - custom_accuracy: 0.8750 - val_loss: 0.5995 - val_custom_accuracy: 0.8542 Epoch 10/25 7/7 [==============================] - 1s 134ms/step - loss: 0.5887 - custom_accuracy: 0.8661 - val_loss: 0.5655 - val_custom_accuracy: 0.8333 Epoch 11/25 7/7 [==============================] - 1s 144ms/step - loss: 0.5796 - custom_accuracy: 0.8482 - val_loss: 0.5681 - val_custom_accuracy: 0.8333 Epoch 12/25 7/7 [==============================] - 1s 143ms/step - loss: 0.5630 - custom_accuracy: 0.7946 - val_loss: 0.5179 - val_custom_accuracy: 0.8333 Epoch 13/25 7/7 [==============================] - 1s 137ms/step - loss: 0.5405 - custom_accuracy: 0.8304 - val_loss: 0.5003 - val_custom_accuracy: 0.8333 Epoch 14/25 7/7 [==============================] - 1s 138ms/step - loss: 0.5259 - custom_accuracy: 0.8036 - val_loss: 0.4787 - val_custom_accuracy: 0.8333 Epoch 15/25 7/7 [==============================] - 1s 137ms/step - loss: 0.5077 - custom_accuracy: 0.8482 - val_loss: 0.4741 - val_custom_accuracy: 0.8125 Epoch 16/25 7/7 [==============================] - 1s 136ms/step - loss: 0.5082 - custom_accuracy: 0.8214 - val_loss: 0.4739 - val_custom_accuracy: 0.8125 Epoch 17/25 7/7 [==============================] - 1s 137ms/step - loss: 0.5138 - custom_accuracy: 0.8214 - val_loss: 0.4859 - val_custom_accuracy: 0.8750 Epoch 18/25 7/7 [==============================] - 1s 133ms/step - loss: 0.5073 - custom_accuracy: 0.8304 - val_loss: 0.4879 - val_custom_accuracy: 0.8333 Epoch 19/25 7/7 [==============================] - 1s 138ms/step - loss: 0.5084 - custom_accuracy: 0.8304 - val_loss: 0.4745 - val_custom_accuracy: 0.8542 Epoch 20/25 7/7 [==============================] - 1s 139ms/step - loss: 0.5057 - custom_accuracy: 0.8571 - val_loss: 0.4702 - val_custom_accuracy: 0.8333 Epoch 21/25 7/7 [==============================] - 1s 135ms/step - loss: 0.4939 - custom_accuracy: 0.8304 - val_loss: 0.4734 - val_custom_accuracy: 0.8750 Epoch 22/25 7/7 [==============================] - 1s 138ms/step - loss: 0.4942 - custom_accuracy: 0.8750 - val_loss: 0.4725 - val_custom_accuracy: 0.8750 Epoch 23/25 7/7 [==============================] - 1s 140ms/step - loss: 0.4982 - custom_accuracy: 0.9107 - val_loss: 0.4695 - val_custom_accuracy: 0.8958 Epoch 24/25 7/7 [==============================] - 1s 135ms/step - loss: 0.4936 - custom_accuracy: 0.8661 - val_loss: 0.4731 - val_custom_accuracy: 0.8750 Epoch 25/25 7/7 [==============================] - 1s 136ms/step - loss: 0.4866 - custom_accuracy: 0.8571 - val_loss: 0.4631 - val_custom_accuracy: 0.8958
plt.plot(history.history['loss'][1:], label='Training')
plt.plot(history.history['val_loss'][1:], label='Validation')
plt.title('Training a Quantum CNN to Detect Excited Cluster States')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

2. 하이브리드 모델
양자 컨볼루션을 사용하여 8개 큐비트에서 1개 큐비트로 이동할 필요가 없습니다. 양자 컨볼루션을 한두 번 수행하고 그 결과를 고전적인 신경망에 입력할 수 있습니다. 이 섹션에서는 양자-고전 하이브리드 모델을 살펴봅니다.
2.1 단일 양자 필터가 있는 하이브리드 모델
모든 비트에서 \(\langle \hat{Z}_n \rangle\) 를 읽은 다음 조밀하게 연결된 신경망이 뒤따르는 양자 컨볼루션의 한 레이어를 적용합니다.

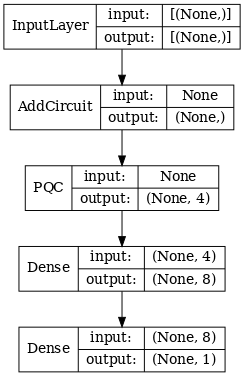
2.1.1 모델 정의
# 1-local operators to read out
readouts = [cirq.Z(bit) for bit in cluster_state_bits[4:]]
def multi_readout_model_circuit(qubits):
"""Make a model circuit with less quantum pool and conv operations."""
model_circuit = cirq.Circuit()
symbols = sympy.symbols('qconv0:21')
model_circuit += quantum_conv_circuit(qubits, symbols[0:15])
model_circuit += quantum_pool_circuit(qubits[:4], qubits[4:],
symbols[15:21])
return model_circuit
# Build a model enacting the logic in 2.1 of this notebook.
excitation_input_dual = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
cluster_state_dual = tfq.layers.AddCircuit()(
excitation_input_dual, prepend=cluster_state_circuit(cluster_state_bits))
quantum_model_dual = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_dual)
d1_dual = tf.keras.layers.Dense(8)(quantum_model_dual)
d2_dual = tf.keras.layers.Dense(1)(d1_dual)
hybrid_model = tf.keras.Model(inputs=[excitation_input_dual], outputs=[d2_dual])
# Display the model architecture
tf.keras.utils.plot_model(hybrid_model,
show_shapes=True,
show_layer_names=False,
dpi=70)
2.1.2 모델 훈련
hybrid_model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.losses.mse,
metrics=[custom_accuracy])
hybrid_history = hybrid_model.fit(x=train_excitations,
y=train_labels,
batch_size=16,
epochs=25,
verbose=1,
validation_data=(test_excitations,
test_labels))
Epoch 1/25 7/7 [==============================] - 1s 113ms/step - loss: 0.9848 - custom_accuracy: 0.5179 - val_loss: 0.9635 - val_custom_accuracy: 0.5417 Epoch 2/25 7/7 [==============================] - 1s 86ms/step - loss: 0.8095 - custom_accuracy: 0.6339 - val_loss: 0.6800 - val_custom_accuracy: 0.7083 Epoch 3/25 7/7 [==============================] - 1s 85ms/step - loss: 0.4045 - custom_accuracy: 0.9375 - val_loss: 0.3342 - val_custom_accuracy: 0.8750 Epoch 4/25 7/7 [==============================] - 1s 86ms/step - loss: 0.2308 - custom_accuracy: 0.9643 - val_loss: 0.2027 - val_custom_accuracy: 0.9792 Epoch 5/25 7/7 [==============================] - 1s 84ms/step - loss: 0.2232 - custom_accuracy: 0.9554 - val_loss: 0.1761 - val_custom_accuracy: 1.0000 Epoch 6/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1760 - custom_accuracy: 0.9821 - val_loss: 0.2541 - val_custom_accuracy: 0.9167 Epoch 7/25 7/7 [==============================] - 1s 85ms/step - loss: 0.1919 - custom_accuracy: 0.9643 - val_loss: 0.1967 - val_custom_accuracy: 0.9792 Epoch 8/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1892 - custom_accuracy: 0.9554 - val_loss: 0.1870 - val_custom_accuracy: 0.9792 Epoch 9/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1777 - custom_accuracy: 0.9911 - val_loss: 0.2208 - val_custom_accuracy: 0.9583 Epoch 10/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1728 - custom_accuracy: 0.9732 - val_loss: 0.2147 - val_custom_accuracy: 0.9583 Epoch 11/25 7/7 [==============================] - 1s 85ms/step - loss: 0.1704 - custom_accuracy: 0.9732 - val_loss: 0.1810 - val_custom_accuracy: 0.9792 Epoch 12/25 7/7 [==============================] - 1s 85ms/step - loss: 0.1739 - custom_accuracy: 0.9732 - val_loss: 0.2038 - val_custom_accuracy: 0.9792 Epoch 13/25 7/7 [==============================] - 1s 81ms/step - loss: 0.1705 - custom_accuracy: 0.9732 - val_loss: 0.1855 - val_custom_accuracy: 0.9792 Epoch 14/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1788 - custom_accuracy: 0.9643 - val_loss: 0.2152 - val_custom_accuracy: 0.9583 Epoch 15/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1760 - custom_accuracy: 0.9732 - val_loss: 0.1994 - val_custom_accuracy: 1.0000 Epoch 16/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1737 - custom_accuracy: 0.9732 - val_loss: 0.2035 - val_custom_accuracy: 0.9792 Epoch 17/25 7/7 [==============================] - 1s 82ms/step - loss: 0.1749 - custom_accuracy: 0.9911 - val_loss: 0.1983 - val_custom_accuracy: 0.9583 Epoch 18/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1875 - custom_accuracy: 0.9732 - val_loss: 0.1916 - val_custom_accuracy: 0.9583 Epoch 19/25 7/7 [==============================] - 1s 82ms/step - loss: 0.1605 - custom_accuracy: 0.9732 - val_loss: 0.1782 - val_custom_accuracy: 0.9792 Epoch 20/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1668 - custom_accuracy: 0.9911 - val_loss: 0.2276 - val_custom_accuracy: 0.9583 Epoch 21/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1700 - custom_accuracy: 0.9911 - val_loss: 0.2080 - val_custom_accuracy: 0.9583 Epoch 22/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1621 - custom_accuracy: 0.9732 - val_loss: 0.1851 - val_custom_accuracy: 0.9375 Epoch 23/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1695 - custom_accuracy: 0.9911 - val_loss: 0.1882 - val_custom_accuracy: 0.9792 Epoch 24/25 7/7 [==============================] - 1s 82ms/step - loss: 0.1583 - custom_accuracy: 0.9911 - val_loss: 0.2017 - val_custom_accuracy: 0.9583 Epoch 25/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1557 - custom_accuracy: 0.9911 - val_loss: 0.1907 - val_custom_accuracy: 0.9792
plt.plot(history.history['val_custom_accuracy'], label='QCNN')
plt.plot(hybrid_history.history['val_custom_accuracy'], label='Hybrid CNN')
plt.title('Quantum vs Hybrid CNN performance')
plt.xlabel('Epochs')
plt.legend()
plt.ylabel('Validation Accuracy')
plt.show()

보시다시피, 매우 적당한 고전적 지원으로 하이브리드 모델은 일반적으로 순수한 양자 버전보다 빠르게 수렴됩니다.
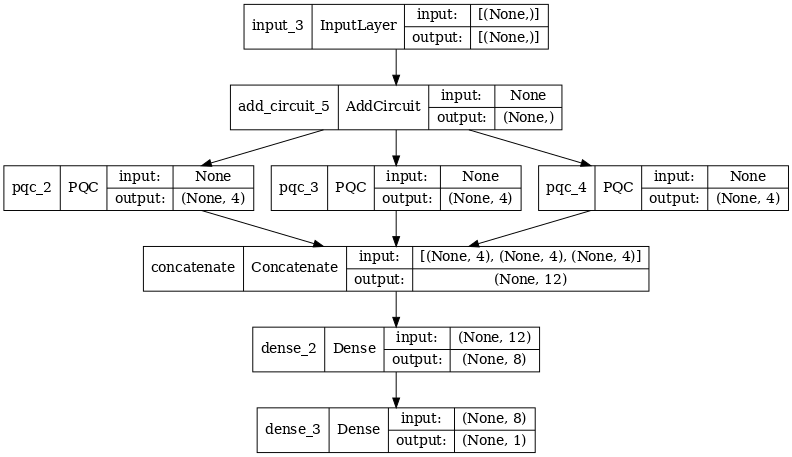
2.2 다중 양자 필터를 사용한 하이브리드 컨볼루션
이제 다중 양자 회선과 고전적인 신경망을 사용하여 이를 결합하는 아키텍처를 사용해 보겠습니다.

2.2.1 모델 정의
excitation_input_multi = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
cluster_state_multi = tfq.layers.AddCircuit()(
excitation_input_multi, prepend=cluster_state_circuit(cluster_state_bits))
# apply 3 different filters and measure expectation values
quantum_model_multi1 = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_multi)
quantum_model_multi2 = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_multi)
quantum_model_multi3 = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_multi)
# concatenate outputs and feed into a small classical NN
concat_out = tf.keras.layers.concatenate(
[quantum_model_multi1, quantum_model_multi2, quantum_model_multi3])
dense_1 = tf.keras.layers.Dense(8)(concat_out)
dense_2 = tf.keras.layers.Dense(1)(dense_1)
multi_qconv_model = tf.keras.Model(inputs=[excitation_input_multi],
outputs=[dense_2])
# Display the model architecture
tf.keras.utils.plot_model(multi_qconv_model,
show_shapes=True,
show_layer_names=True,
dpi=70)
2.2.2 모델 훈련
multi_qconv_model.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.losses.mse,
metrics=[custom_accuracy])
multi_qconv_history = multi_qconv_model.fit(x=train_excitations,
y=train_labels,
batch_size=16,
epochs=25,
verbose=1,
validation_data=(test_excitations,
test_labels))
Epoch 1/25 7/7 [==============================] - 2s 143ms/step - loss: 0.9425 - custom_accuracy: 0.6429 - val_loss: 0.8120 - val_custom_accuracy: 0.7083 Epoch 2/25 7/7 [==============================] - 1s 109ms/step - loss: 0.5778 - custom_accuracy: 0.7946 - val_loss: 0.5920 - val_custom_accuracy: 0.7500 Epoch 3/25 7/7 [==============================] - 1s 103ms/step - loss: 0.4954 - custom_accuracy: 0.9018 - val_loss: 0.4568 - val_custom_accuracy: 0.7708 Epoch 4/25 7/7 [==============================] - 1s 95ms/step - loss: 0.2855 - custom_accuracy: 0.9196 - val_loss: 0.2792 - val_custom_accuracy: 0.9375 Epoch 5/25 7/7 [==============================] - 1s 93ms/step - loss: 0.1902 - custom_accuracy: 0.9821 - val_loss: 0.2212 - val_custom_accuracy: 0.9375 Epoch 6/25 7/7 [==============================] - 1s 94ms/step - loss: 0.1685 - custom_accuracy: 0.9821 - val_loss: 0.2341 - val_custom_accuracy: 0.9583 Epoch 7/25 7/7 [==============================] - 1s 104ms/step - loss: 0.1671 - custom_accuracy: 0.9911 - val_loss: 0.2062 - val_custom_accuracy: 0.9792 Epoch 8/25 7/7 [==============================] - 1s 97ms/step - loss: 0.1511 - custom_accuracy: 0.9821 - val_loss: 0.2096 - val_custom_accuracy: 0.9792 Epoch 9/25 7/7 [==============================] - 1s 96ms/step - loss: 0.1432 - custom_accuracy: 0.9911 - val_loss: 0.2330 - val_custom_accuracy: 0.9375 Epoch 10/25 7/7 [==============================] - 1s 92ms/step - loss: 0.1668 - custom_accuracy: 0.9821 - val_loss: 0.2344 - val_custom_accuracy: 0.9583 Epoch 11/25 7/7 [==============================] - 1s 106ms/step - loss: 0.1893 - custom_accuracy: 0.9732 - val_loss: 0.2148 - val_custom_accuracy: 0.9583 Epoch 12/25 7/7 [==============================] - 1s 104ms/step - loss: 0.1857 - custom_accuracy: 0.9732 - val_loss: 0.2739 - val_custom_accuracy: 0.9583 Epoch 13/25 7/7 [==============================] - 1s 106ms/step - loss: 0.1748 - custom_accuracy: 0.9732 - val_loss: 0.2366 - val_custom_accuracy: 0.9583 Epoch 14/25 7/7 [==============================] - 1s 103ms/step - loss: 0.1515 - custom_accuracy: 0.9821 - val_loss: 0.2012 - val_custom_accuracy: 0.9583 Epoch 15/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1552 - custom_accuracy: 0.9911 - val_loss: 0.2404 - val_custom_accuracy: 0.9375 Epoch 16/25 7/7 [==============================] - 1s 97ms/step - loss: 0.1572 - custom_accuracy: 0.9911 - val_loss: 0.2779 - val_custom_accuracy: 0.9375 Epoch 17/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1546 - custom_accuracy: 0.9821 - val_loss: 0.2104 - val_custom_accuracy: 0.9583 Epoch 18/25 7/7 [==============================] - 1s 102ms/step - loss: 0.1418 - custom_accuracy: 0.9911 - val_loss: 0.2647 - val_custom_accuracy: 0.9583 Epoch 19/25 7/7 [==============================] - 1s 98ms/step - loss: 0.1590 - custom_accuracy: 0.9732 - val_loss: 0.2154 - val_custom_accuracy: 0.9583 Epoch 20/25 7/7 [==============================] - 1s 104ms/step - loss: 0.1363 - custom_accuracy: 1.0000 - val_loss: 0.2470 - val_custom_accuracy: 0.9375 Epoch 21/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1442 - custom_accuracy: 0.9821 - val_loss: 0.2383 - val_custom_accuracy: 0.9375 Epoch 22/25 7/7 [==============================] - 1s 99ms/step - loss: 0.1415 - custom_accuracy: 0.9911 - val_loss: 0.2324 - val_custom_accuracy: 0.9583 Epoch 23/25 7/7 [==============================] - 1s 97ms/step - loss: 0.1424 - custom_accuracy: 0.9821 - val_loss: 0.2188 - val_custom_accuracy: 0.9583 Epoch 24/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1417 - custom_accuracy: 0.9821 - val_loss: 0.2340 - val_custom_accuracy: 0.9375 Epoch 25/25 7/7 [==============================] - 1s 103ms/step - loss: 0.1471 - custom_accuracy: 0.9732 - val_loss: 0.2252 - val_custom_accuracy: 0.9583
plt.plot(history.history['val_custom_accuracy'][:25], label='QCNN')
plt.plot(hybrid_history.history['val_custom_accuracy'][:25], label='Hybrid CNN')
plt.plot(multi_qconv_history.history['val_custom_accuracy'][:25],
label='Hybrid CNN \n Multiple Quantum Filters')
plt.title('Quantum vs Hybrid CNN performance')
plt.xlabel('Epochs')
plt.legend()
plt.ylabel('Validation Accuracy')
plt.show()

