برنامه نویسی احتمالی در Oryx

pip install -q -U jax jaxlib
pip install -q -Uq oryx -I
pip install -q tfp-nightly --upgrade

from functools import partial

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')

import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random

from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions

import oryx

برنامه نویسی احتمالی این ایده است که ما می توانیم مدل های احتمالی را با استفاده از ویژگی های یک زبان برنامه نویسی بیان کنیم. سپس کارهایی مانند استنتاج بیزی یا حاشیه سازی به عنوان ویژگی های زبان ارائه می شوند و به طور بالقوه می توانند خودکار شوند.

Oryx یک سیستم برنامه نویسی احتمالی را ارائه می دهد که در آن برنامه های احتمالی فقط به عنوان توابع پایتون بیان می شوند. این برنامه‌ها سپس از طریق تبدیل‌های تابع قابل ترکیب مانند آنهایی که در JAX هستند، تبدیل می‌شوند! ایده این است که با برنامه‌های ساده شروع کنیم (مانند نمونه‌برداری از یک نرمال تصادفی) و آنها را با هم ترکیب کنیم تا مدل‌هایی را تشکیل دهیم (مانند شبکه عصبی بیزی). یک نکته مهم از طراحی PPL اوریکس این است که قادر می سازد برنامه به مانند توابع شما در حال حاضر می خواهم ارسال و استفاده در JAX نگاه کنید، اما هستند و مشروح به تحولات از آنها آگاه است.

بیایید ابتدا عملکرد اصلی PPL Oryx را وارد کنیم.

from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest

برنامه های احتمالی در Oryx چیست؟

در Oryx، برنامه‌های احتمالی فقط توابع پایتون خالص هستند که بر روی مقادیر JAX و کلیدهای شبه تصادفی عمل می‌کنند و یک نمونه تصادفی را برمی‌گردانند. با طراحی، آنها سازگار با تحولات مانند jit و vmap . با این حال، سیستم های برنامه نویسی احتمالاتی اوریکس ابزار است که شما را قادر به حاشیه نویسی توابع خود را در راه مفید است.

پس از فلسفه JAX از توابع خالص، یک برنامه احتمالی اوریکس یک تابع پایتون که طول می کشد JAX است PRNGKey به عنوان آرگومان اول و هر تعداد آرگومان تهویه متعاقب آن. خروجی تابع "نمونه" و محدودیت های که به درخواست به نام jit -ed و vmap توابع -ed به برنامه های احتمالی (به عنوان مثال هیچ جریان وابسته به داده های کنترل، هیچ عوارض جانبی، و غیره) اعمال می شود. این با بسیاری از سیستم‌های برنامه‌نویسی احتمالی ضروری که در آنها یک «نمونه» کل ردیابی اجرا، از جمله مقادیر داخلی اجرای برنامه است، متفاوت است. خواهیم دید که چگونه می توانید اوریکس ارزش های داخلی با استفاده از دسترسی به joint_sample ، مورد بحث قرار گرفته است.

Program :: PRNGKey -> ... -> Sample

در اینجا یک برنامه "سلام جهان" است که نمونه ها از توزیع لوگ نرمال .

def log_normal(key):
  return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))

print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
0.8139614
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

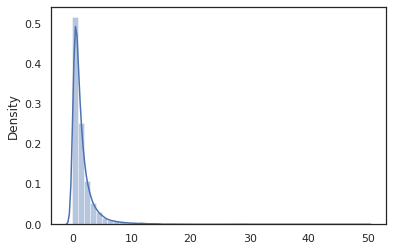
log_normal تابع لفاف بسته بندی نازک در اطراف یک است Tensorflow احتمال (TFP) توزیع، اما به جای فراخوانی tfd.Normal(0., 1.).sample ، ما استفاده کرده ایم random_variable به جای. همانطور که بعدا خواهیم دید، random_variable ما را قادر به تبدیل اشیاء را به برنامه های احتمالی، همراه با دیگر قابلیت های مفید.

ما می توانیم تبدیل log_normal را به یک تابع ورود به سیستم با چگالی با استفاده از log_prob تحول:

print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()

-0.9189385

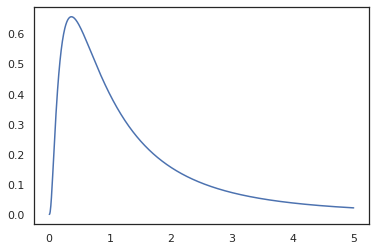
از آنجا که ما تابع با مشروح این random_variable ، log_prob آگاه است که یک تماس به وجود tfd.Normal(0., 1.).sample و با استفاده از tfd.Normal(0., 1.).log_prob برای محاسبه توزیع پایه مشکل ورود برای رسیدگی به jnp.exp ، ppl.log_prob به طور خودکار محاسبه تراکم از طریق توابع دوسویی، پیگیری تغییرات حجم در محاسبه تغییر از متغیر.

در اوریکس، ما می توانیم برنامه ها و تبدیل آنها با استفاده از تحولات تابع - برای مثال، jax.jit یا log_prob . البته Oryx نمی تواند این کار را با هیچ برنامه ای انجام دهد. به توابع نمونه‌گیری نیاز دارد که تابع چگالی log خود را با Oryx ثبت کرده باشند. خوشبختانه، اوریکس به طور خودکار TensorFlow احتمال توزیع (TFP) در سیستم آن است.

ابزارهای برنامه نویسی احتمالی Oryx

Oryx چندین تغییر تابع دارد که به سمت برنامه‌نویسی احتمالی تنظیم شده‌اند. ما به بیشتر آنها می پردازیم و نمونه هایی را ارائه می دهیم. در پایان، همه آن‌ها را در یک مطالعه موردی MCMC قرار می‌دهیم. شما همچنین می توانید به اسناد و مدارک برای مراجعه core.ppl.transformations برای جزئیات بیشتر.

random_variable

random_variable دو قطعه اصلی قابلیت، هر دو در حاشیه نویسی توابع پایتون با اطلاعات است که می تواند در تحولات استفاده متمرکز شده است.

1. random_variable ، عمل به عنوان تابع هویت به طور پیش فرض، اما می تواند ثبت نام نوع خاص به اشیاء تبدیل به programs.` احتمالاتی استفاده

   انواع قابل فراخوانی (توابع پایتون لامبداها، functools.partial بازدید کنندگان، و غیره) و خودسرانه object بازدید کنندگان (مانند JAX DeviceArray بازدید کنندگان) این فقط ورودی آن باز خواهد گشت.

   random_variable(x: object) == x
   random_variable(f: Callable[...]) == f
   

   غزال به طور خودکار TensorFlow احتمال (TFP) توزیع، که به برنامه های احتمالی که توزیع را پاسخ تبدیل sample روش.

   random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235
   

   Oryx علاوه بر این اطلاعات مربوط به توزیع TFP را در ردیابی های JAX تعبیه می کند که امکان محاسبه خودکار چگالی گزارش ها را فراهم می کند.

2. random_variable ارزش های برچسب می توانید با نام، آنها را برای تحولات پایین دست مفید است، با ارائه یک اختیاری name استدلال کلمه کلیدی را به random_variable . هنگامی که ما یک آرایه را تصویب به random_variable همراه با name (به عنوان مثال random_variable(x, name='x') )، آن را فقط برچسب ارزش و بازده آن. اگر ما در یک، قابل فراخوانی و یا توزیع TFP عبور random_variable بازده برنامه ای است که دستورات نمونه خروجی آن با name .

این یادداشت ها معناشناسی برنامه تغییر دهید زمانی که اجرا می شود، اما تنها زمانی که تبدیل (یعنی برنامه ارزش با یا بدون استفاده از بازگشت random_variable ).

بیایید مثالی را مرور کنیم که در آن از هر دو بخش عملکرد با هم استفاده می کنیم.

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

در این برنامه ما به واسطه کلیدواژه z و x ، که باعث می تحولات joint_sample ، intervene ، conditional و graph_replace از نام آگاه 'z' و 'x' . در ادامه به نحوه استفاده از نام‌ها توسط هر تبدیل خواهیم پرداخت.

log_prob

log_prob تحول تابع یک برنامه احتمالی اوریکس به تابع ورود چگالی آن تبدیل می کند. این تابع log-density یک نمونه بالقوه از برنامه را به عنوان ورودی می گیرد و لگ چگالی آن را تحت توزیع نمونه گیری زیربنایی برمی گرداند.

log_prob :: Program -> (Sample -> LogDensity)

مانند random_variable ، آن را از طریق رجیستری از انواع که در آن توزیع بهره وری کل عوامل به طور خودکار ثبت کار می کند، به طوری که log_prob(tfd.Normal(0., 1.)) می نامد tfd.Normal(0., 1.).log_prob . برای توابع پایتون، با این حال، log_prob آثار برنامه با استفاده از JAX و به نظر می رسد برای نمونه برداری اظهارات. log_prob تحول این نسخهها کار در اکثر برنامه هایی که متغیرهای تصادفی بازگشت، به طور مستقیم و یا از طریق تحولات وارون اما نه در برنامه هایی که مقادیر نمونه داخلی که بازگشت نیست. اگر آن را می توانید عملیات لازم در برنامه معکوس نیست، log_prob خواهد خطا بزنند.

در اینجا چند نمونه از می log_prob اعمال شده به برنامه های مختلف.

1. log_prob این نسخهها کار در برنامه هایی که به طور مستقیم نمونه از توزیع های بهره وری کل عوامل (یا دیگر انواع ثبت نام شده) و بازگشت ارزش های خود را.

def normal(key):
  return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))

-0.9189385

1. log_prob قادر به محاسبه ورود تراکم نمونه ها از برنامه هایی که تبدیل متغیرهای تصادفی با استفاده از توابع bijective است (به عنوان مثال jnp.exp ، jnp.tanh ، jnp.split ).

def log_normal(key):
  return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))

-1.159165

به منظور محاسبه یک نمونه از log_normal را ورود به سیستم با چگالی، ما اول نیاز به معکوس exp ، در نظر گرفتن log از نمونه، و سپس اضافه کردن تصحیح حجم تغییر با استفاده از ورود DET معکوس ژاکوبین از exp (را ببینید تغییر متغیر فرمول از ویکیپدیا).

1. log_prob آثار با برنامه هایی که ساختار خروجی از نمونه را دوست دارید، واژه نامه ها پایتون یا چندتایی ها.

def normal_2d(key):
  x = random_variable(
    tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
  x1, x2 = jnp.split(x, 2, 0)
  return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))

{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546

1. log_prob پیاده روی نمودار محاسبات ترسیم تابع، محاسبه مقادیر رو به جلو و معکوس (و ورود DET خود Jacobians) در صورت لزوم در تلاش برای اتصال مقادیر بازگردانده با ارزش نمونه پایه خود را از طریق یک تغییر به خوبی تعریف متغیر. نمونه برنامه زیر را در نظر بگیرید:

def complex_program(key):
  k1, k2 = random.split(key)
  z = random_variable(tfd.Normal(0., 1.))(k1)
  x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
  return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))

(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32))
-1.0967848

در این برنامه، ما نمونه x مشروط بر z ، به این معنی که ما نیاز ارزش z قبل از ما می توانید ورود به سیستم تراکم محاسبه x . با این حال، به منظور محاسبه z ، ابتدا باید معکوس jnp.exp اعمال شده به z . بنابراین، به منظور محاسبه ورود تراکم x و z ، log_prob نیازهای به اولین معکوس خروجی اول، و سپس تصویب آن جلو را از طریق jax.nn.relu برای محاسبه میانگین p(x | z) .

توجه: در حالی که log_prob کار بر روی برنامه هایی که متغیرهای تصادفی نمونه که به عنوان خروجی برگردانده نشده است، نمی joint_sample می توانید یک برنامه را به یکی که می کند تبدیل کنید.

برای کسب اطلاعات بیشتر در مورد log_prob ، شما می توانید برای اشاره core.interpreters.log_prob . در اجرا، log_prob است که از نزدیک کردن از اساس inverse تحول JAX؛ برای کسب اطلاعات بیشتر در مورد inverse ، و core.interpreters.inverse .

joint_sample

برای تعریف برنامه‌های پیچیده‌تر و جالب‌تر، از چند متغیر تصادفی پنهان، یعنی متغیرهای تصادفی با مقادیر مشاهده نشده استفاده می‌کنیم. اجازه دهید به مراجعه latent_normal برنامه ای است که نمونه یک مقدار تصادفی z است که به عنوان یکی دیگر از میانگین مقدار تصادفی استفاده x .

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

در این برنامه، z بنابراین نهفته اگر ما به تنها پاسخ است latent_normal(random.PRNGKey(0)) ما ارزش واقعی مطمئن شوید که z است که مسئول تولید x .

joint_sample یک تغییر و تحول است که تبدیل یک برنامه به برنامه دیگر که بازده یک فرهنگ لغت نام رشته نقشه برداری (برچسب ها) به ارزش های خود. برای اینکه کار کنیم، باید مطمئن شویم که متغیرهای پنهان را برچسب گذاری کرده ایم تا مطمئن شویم که در خروجی تابع تبدیل شده ظاهر می شوند.

joint_sample(latent_normal)(random.PRNGKey(0))

{'x': DeviceArray(0.01873656, dtype=float32),
 'z': DeviceArray(0.14389044, dtype=float32)}

توجه داشته باشید که joint_sample تبدیل یک برنامه به برنامه دیگر که نمونه توزیع مشترک بر سر ارزشهای نهفته خود را، به طوری که ما می توانیم بیشتر از آن را متحول کند. برای الگوریتم هایی مانند MCMC و VI، محاسبه احتمال ورود به سیستم توزیع مشترک به عنوان بخشی از روش استنتاج معمول است. log_prob(latent_normal) کار نمی کند چرا که نیاز به حاشیه راندن خارج z ، اما ما می توانید استفاده کنید log_prob(joint_sample(latent_normal)) .

print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))

-50.03529
-5049.535

از آنجا که این چنین الگوی رایج است، اوریکس همچنین دارای یک joint_log_prob تحول است که فقط از ترکیب log_prob و joint_sample .

print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))

-50.03529
-5049.535

block

block تحول طول می کشد در یک برنامه و یک دنباله از نام ها و برنامه ای است که رفتار یکسان با این تفاوت که در تحولات پایین دست (مانند گرداند joint_sample )، نام ارائه نادیده گرفته می شوند. یک نمونه از آن block مفید است تبدیل به یک توزیع مشترک به یک قبل بر متغیرهای نهفته شده توسط "مسدود کردن" ارزش ها نمونه در احتمال. به عنوان مثال، latent_normal که برای اولین بار تساوی یک z ~ N(0, 1) پس از آن یک x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) یک برنامه است که پنهان است x نام، بنابراین اگر ما joint_sample(block(latent_normal, names=['x'])) ، ما یک فرهنگ لغت تنها با به دست آوردن z در آن .

blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))

{'z': DeviceArray(0.14389044, dtype=float32)}

intervene

intervene clobbers تحول نمونه در یک برنامه احتمالی با ارزش از خارج. رفتن به ما latent_normal برنامه، اجازه دهید بگویم ما در حال اجرا برنامه همان علاقه مند بودند اما می خواستم z به جای 4. ثابت شود از نوشتن یک برنامه جدید، ما می توانیم با استفاده از intervene به نادیده گرفتن ارزش z .

intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();

/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

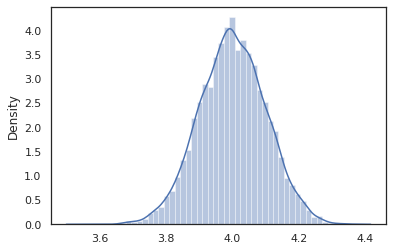
intervened نمونه تابع از p(x | do(z = 4)) است که فقط یک توزیع نرمال استاندارد محور در 4. هنگامی که ما intervene در یک مقدار خاص، که ارزش دیگر یک متغیر تصادفی در نظر گرفته. این بدان معنی است که z ارزش خواهد شد در حالی برچسب نمی شود اجرای intervened .

conditional

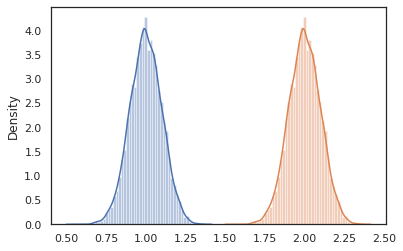
conditional تبدیل برنامه ای است که نمونه نهفته ارزش را به یکی که شرایط در آن ارزش ها نهفته است. بازگشت به ما latent_normal برنامه، که نمونه p(x) با پنهان z ، ما می توانیم آن را به یک برنامه مشروط تبدیل p(x | z) .

cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()

99.87485
49.874847
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

nest

هنگامی که ما شروع به نوشتن برنامه های احتمالی برای ساختن برنامه های پیچیده تر می کنیم، استفاده مجدد از توابعی که دارای منطق مهمی هستند معمول است. برای مثال، اگر ما می خواهم برای ساخت یک شبکه عصبی بیزی، ممکن است مهم dense برنامه ای است که نمونه وزن و اجرا یک پاس رو به جلو.

اگر ما توابع استفاده مجدد، با این حال، ما ممکن است با ارزش برچسب گذاشته شده توسط های تکراری در برنامه نهایی، است که توسط تحولات مانند مجاز پایان joint_sample . ما می توانیم با استفاده از nest به ایجاد برچسب "حوزه" که در آن هر نمونه ها در داخل از یک دامنه به نام خواهد شد را به یک فرهنگ لغت تو در تو قرار داده است.

def f(key):
  return random_variable(tfd.Normal(0., 1.), name='x')(key)

def g(key):
  k1, k2 = random.split(key)
  return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))

{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
 'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }

مطالعه موردی: شبکه عصبی بیزی

بیایید دست ما در آموزش شبکه عصبی بیزی برای طبقه بندی کلاسیک سعی کنید فیشر جنس زنبق و سوسن مجموعه داده. نسبتاً کوچک و کم‌بعد است، بنابراین می‌توانیم مستقیماً نمونه‌برداری پشتی را با MCMC امتحان کنیم.

ابتدا، بیایید مجموعه داده و برخی ابزارهای دیگر را از Oryx وارد کنیم.

from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']

num_features = features.shape[-1]
num_classes = len(iris.target_names)

from oryx.experimental import mcmc
from oryx.util import summary, get_summaries

ما با اجرای یک لایه متراکم شروع می کنیم، که دارای اولویت های عادی نسبت به وزن ها و بایاس است. برای انجام این کار، ابتدا یک تعریف dense تابع مرتبه بالاتر که طول می کشد در بعد خروجی و فعال سازی تابع مورد نظر. dense تابع یک برنامه احتمالاتی است که نشان دهنده یک توزیع مشروط گرداند p(h | x) که در آن h از خروجی یک لایه متراکم است و x ورودی آن است. این برای اولین بار نمونه وزن و تعصب و سپس آنها را به اعمال x .

def dense(dim_out, activation=jax.nn.relu):
  def forward(key, x):
    dim_in = x.shape[-1]
    w_key, b_key = random.split(key)
    w = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
          name='w')(w_key)
    b = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
          name='b')(b_key)
    return activation(jnp.dot(w, x) + b)
  return forward

به سرودن چند dense لایه با هم، ما یک اجرای mlp (پرسپترون چند) تابع مرتبه بالاتر که طول می کشد در یک لیست از اندازه های مخفی و تعدادی از کلاس های. این برنامه ای است که بارها و بارها خواستار گرداند dense با استفاده از مناسب hidden_size و در نهایت می گرداند logits برای هر کلاس در لایه نهایی. توجه داشته باشید که استفاده از nest که ایجاد نام حوزه برای هر لایه.

def mlp(hidden_sizes, num_classes):
  num_hidden = len(hidden_sizes)
  def forward(key, x):
    keys = random.split(key, num_hidden + 1)
    for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
      x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
    logits = nest(dense(num_classes, activation=lambda x: x),
                  scope=f'layer_{num_hidden + 1}')(keys[-1], x)
    return logits
  return forward

برای پیاده سازی مدل کامل، باید برچسب ها را به عنوان متغیرهای تصادفی طبقه بندی کنیم. ما تعریف یک predict عملکرد که طول می کشد در یک مجموعه از xs (ویژگی های) هستند که پس از به تصویب mlp با استفاده از vmap . هنگامی که ما با استفاده از vmap(partial(mlp, mlp_key)) ، ما نمونه یک مجموعه واحد از وزن، اما نقشه پاس رو به جلو بیش از همه ورودی xs . این تولید مجموعه ای از logits که parameterizes توزیع طبقه مستقل است.

def predict(mlp):
  def forward(key, xs):
    mlp_key, label_key = random.split(key)
    logits = vmap(partial(mlp, mlp_key))(xs)
    return random_variable(
        tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
  return forward

این مدل کامل است! بیایید از MCMC برای نمونه برداری از داده های داده شده وزن BNN استفاده کنیم. در ابتدا ما یک BNN "قالب" ساخت با استفاده از mlp .

bnn = mlp([200, 200], num_classes)

برای ساخت یک نقطه شروع برای زنجیره مارکوف ما، ما می توانید استفاده کنید joint_sample با یک ورودی ساختگی.

weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())

dict_keys(['layer_1', 'layer_2', 'layer_3'])

محاسبه احتمال گزارش توزیع مشترک برای بسیاری از الگوریتم‌های استنتاج کافی است. اکنون بیایید می گویند که ما مشاهده x و می خواهید برای نمونه خلفی p(z | x) . برای توزیع پیچیده، ما قادر نخواهد بود برای به حاشیه راندن خارج x (هر چند برای latent_normal ما می توانیم) اما ما می توانیم چگالی ورود به سیستم unnormalized محاسبه log p(z, x) که در آن x به یک مقدار خاص ثابت شده است. می‌توانیم از احتمال لاگ غیرعادی‌شده با MCMC برای نمونه‌برداری از قسمت خلفی استفاده کنیم. بیایید این تابع log prob "پین شده" را بنویسیم.

def target_log_prob(weights):
  return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)

در حال حاضر ما می توانید استفاده کنید tfp.mcmc به نمونه خلفی با استفاده از تابع چگالی ورود به سیستم unnormalized ما است. توجه داشته باشید که ما مجبور به استفاده از "مسطح" نسخه از وزن تو در تو ما واژه نامه که سازگار با tfp.mcmc ، بنابراین ما استفاده از آب و برق درخت JAX به صاف و unflatten.

@jit
def run_chain(key, weights):
  flat_state, sample_tree = jax.tree_flatten(weights)

  def flat_log_prob(*states):
    return target_log_prob(jax.tree_unflatten(sample_tree, states))

  def trace_fn(_, results):
    return results.inner_results.accepted_results.target_log_prob

  flat_states, log_probs = tfp.mcmc.sample_chain(
    1000,
    num_burnin_steps=9000,
    kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
        tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
        9000, target_accept_prob=0.7),
    trace_fn=trace_fn,
    current_state=flat_state,
    seed=key)
  samples = jax.tree_unflatten(sample_tree, flat_states)
  return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)

plt.plot(log_probs)
plt.show()

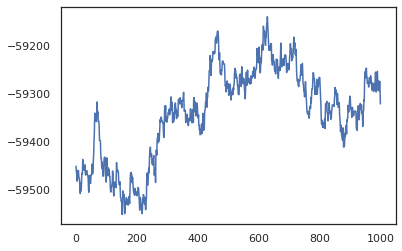
ما می‌توانیم از نمونه‌های خود برای تخمین میانگین‌گیری مدل بیزی (BMA) از دقت تمرین استفاده کنیم. برای محاسبه آن، ما می توانید استفاده کنید intervene با bnn "تزریق" خلفی وزن در محل از آنهایی هستند که از کلید نمونه. برای محاسبه logits برای هر نقطه داده ها برای هر نمونه خلفی، ما می توانیم دو برابر vmap بیش از posterior_weights و features .

output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
    random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)

print('Average sample accuracy:', (
    output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
    output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())

Average sample accuracy: 0.9874067
BMA accuracy: 0.99333334

نتیجه

در Oryx، برنامه های احتمالی فقط توابع JAX هستند که تصادفی (شبه) را به عنوان ورودی می گیرند. به دلیل ادغام شدید Oryx با سیستم تبدیل تابع JAX، می‌توانیم برنامه‌های احتمالی را مانند نوشتن کد JAX بنویسیم و دستکاری کنیم. این منجر به یک سیستم ساده اما انعطاف پذیر برای ساخت مدل های پیچیده و انجام استنتاج می شود.