Programmazione probabilistica in Oryx

pip install -q -U jax jaxlib
pip install -q -Uq oryx -I
pip install -q tfp-nightly --upgrade

from functools import partial

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='white')

import jax
import jax.numpy as jnp
from jax import jit, vmap, grad
from jax import random

from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions

import oryx

La programmazione probabilistica è l'idea che possiamo esprimere modelli probabilistici usando le caratteristiche di un linguaggio di programmazione. Attività come l'inferenza bayesiana o l'emarginazione vengono quindi fornite come funzionalità del linguaggio e possono essere potenzialmente automatizzate.

Oryx fornisce un sistema di programmazione probabilistico in cui i programmi probabilistici sono semplicemente espressi come funzioni Python; questi programmi vengono poi trasformati tramite trasformazioni di funzioni componibili come quelle in JAX! L'idea è di iniziare con programmi semplici (come il campionamento da una normale casuale) e comporli insieme per formare modelli (come una rete neurale bayesiana). Un punto importante del disegno di PPL Oryx è quello di consentire i programmi a guardare come le funzioni che ci si già scrivere e uso di JAX, ma sono annotati per fare trasformazioni a conoscenza.

Per prima cosa importiamo la funzionalità PPL principale di Oryx.

from oryx.core.ppl import random_variable
from oryx.core.ppl import log_prob
from oryx.core.ppl import joint_sample
from oryx.core.ppl import joint_log_prob
from oryx.core.ppl import block
from oryx.core.ppl import intervene
from oryx.core.ppl import conditional
from oryx.core.ppl import graph_replace
from oryx.core.ppl import nest

Quali sono i programmi probabilistici in Oryx?

In Oryx, i programmi probabilistici sono solo funzioni Python pure che operano su valori JAX e chiavi pseudocasuali e restituiscono un campione casuale. In base alla progettazione, sono compatibili con le trasformazioni come jit e vmap . Tuttavia, il sistema di programmazione probabilistico Oryx fornisce strumenti che consentono di annotare le funzioni in modi utili.

Seguendo la filosofia JAX delle funzioni pure, un programma probabilistico Oryx è una funzione Python che prende un JAX PRNGKey come primo argomento e qualsiasi numero di ulteriori argomentazioni di condizionamento. L'uscita della funzione è chiamato "campione" e le stesse restrizioni che valgono per jit -ed e vmap funzioni -ed applicano ai programmi probabilistici (es alcun flusso dipendente dai dati di controllo, senza effetti collaterali, ecc). Questo differisce da molti sistemi di programmazione probabilistica imperativa in cui un "campione" è l'intera traccia di esecuzione, inclusi i valori interni all'esecuzione del programma. Vedremo più avanti come Oryx può accedere valori interni usando l' joint_sample , discusso di seguito.

Program :: PRNGKey -> ... -> Sample

Ecco un programma "ciao mondo" che i campioni provenienti da una distribuzione log-normale .

def log_normal(key):
  return jnp.exp(random_variable(tfd.Normal(0., 1.))(key))

print(log_normal(random.PRNGKey(0)))
sns.distplot(jit(vmap(log_normal))(random.split(random.PRNGKey(0), 10000)))
plt.show()

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
0.8139614
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

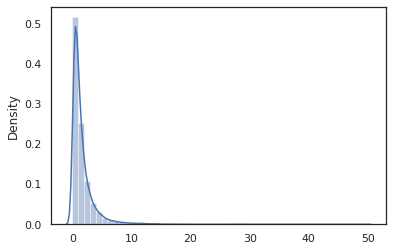
La log_normal funzione è un involucro leggero intorno ad un tensorflow Probabilità (TFP) di distribuzione, ma invece di chiamare tfd.Normal(0., 1.).sample , abbiamo utilizzato random_variable invece. Come vedremo più avanti, random_variable ci permette di convertire gli oggetti in programmi probabilistiche, insieme ad altre funzionalità utili.

Siamo in grado di convertire log_normal in una funzione di log densità utilizzando il log_prob trasformazione:

print(log_prob(log_normal)(1.))
x = jnp.linspace(0., 5., 1000)
plt.plot(x, jnp.exp(vmap(log_prob(log_normal))(x)))
plt.show()

-0.9189385

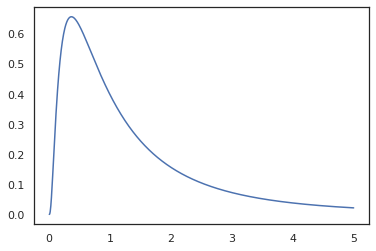
Perché abbiamo annotato la funzione con random_variable , log_prob è consapevole del fatto che c'era una chiamata a tfd.Normal(0., 1.).sample e usa tfd.Normal(0., 1.).log_prob per calcolare la distribuzione di base log prob. Per gestire il jnp.exp , ppl.log_prob calcola automaticamente densità attraverso funzioni biunivoche, tenere traccia dei cambiamenti di volume nel calcolo di cambio di variabile.

In Oryx, siamo in grado di prendere i programmi e trasformarli utilizzando le trasformazioni di funzione - ad esempio, jax.jit o log_prob . Oryx non può farlo con qualsiasi programma però; richiede funzioni di campionamento che hanno registrato la loro funzione di densità logaritmica con Oryx. Fortunatamente, Oryx registra automaticamente tensorflow Probabilità distribuzioni (TFP) nel suo sistema.

Gli strumenti di programmazione probabilistica di Oryx

Oryx ha diverse trasformazioni di funzioni orientate alla programmazione probabilistica. Ne esamineremo la maggior parte e forniremo alcuni esempi. Alla fine, metteremo tutto insieme in un caso di studio MCMC. Si può anche fare riferimento alla documentazione per core.ppl.transformations per maggiori dettagli.

random_variable

random_variable ha due parti principali di funzionalità, entrambi orientati annotando funzioni Python con le informazioni che possono essere utilizzate nelle trasformazioni.

1. random_variable 'opera come la funzione identità di default, ma può usare il tipo-specifici iscrizioni agli oggetti convertire in programs.` probabilistico

   Per i tipi richiamabili (funzioni Python, lambda, functools.partial s, etc.) e arbitrario object s (come JAX DeviceArray s) sarà solo ritorno suo ingresso.

   random_variable(x: object) == x
   random_variable(f: Callable[...]) == f
   

   Oryx registra automaticamente tensorflow Probabilità (PTF) distribuzioni, che vengono convertiti in programmi probabilistiche che chiamano della distribuzione sample metodo.

   random_variable(tfd.Normal(0., 1.))(random.PRNGKey(0)) # ==> -0.20584235
   

   Oryx incorpora inoltre le informazioni sulla distribuzione TFP nelle tracce JAX che consentono il calcolo automatico delle densità dei log.

2. random_variable valori può tag con nomi, che li rende utili per le trasformazioni a valle, fornendo un optional name argomento chiave di random_variable . Quando si passa un array in random_variable oltre ad name (es random_variable(x, name='x') ), solo tag il valore e lo restituisce. Se passiamo in un callable o distribuzione TFP, random_variable restituisce un programma che i tag il suo campione di uscita con name .

Queste annotazioni non cambiano la semantica del programma quando eseguito, ma solo quando trasformato (cioè il programma restituirà lo stesso valore con o senza l'uso di random_variable ).

Esaminiamo un esempio in cui usiamo entrambe le funzionalità insieme.

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

In questo programma abbiamo etichettato l'intermedi z e x , che rende il trasformazioni joint_sample , intervene , conditional e graph_replace a conoscenza dei nomi 'z' e 'x' . Esamineremo esattamente come ogni trasformazione utilizza i nomi in seguito.

log_prob

La log_prob trasformazione funzione converte un programma probabilistica Oryx nella sua funzione di log-densità. Questa funzione log-density prende un potenziale campione dal programma come input e restituisce la sua log-density sotto la distribuzione di campionamento sottostante.

log_prob :: Program -> (Sample -> LogDensity)

Come random_variable , funziona tramite un registro dei tipi in cui le distribuzioni TFP sono registrate automaticamente, in modo da log_prob(tfd.Normal(0., 1.)) chiama tfd.Normal(0., 1.).log_prob . Per le funzioni Python, tuttavia, log_prob ripercorre il programma utilizzando JAX e guarda per il campionamento dichiarazioni. Il log_prob trasformazione funziona sulla maggior parte dei programmi che restituiscono variabili casuali, direttamente o tramite trasformazioni invertibili ma non su programmi che i valori di esempio internamente che non vengono restituiti. Se non è possibile invertire le operazioni necessarie nel programma, log_prob genera un errore.

Ecco alcuni esempi di log_prob applicate ai vari programmi.

1. log_prob lavora su programmi che direttamente dal campione distribuzioni TFP (o altri tipi registrati) e restituire i loro valori.

def normal(key):
  return random_variable(tfd.Normal(0., 1.))(key)
print(log_prob(normal)(0.))

-0.9189385

1. log_prob è in grado di calcolare log-densità di campioni da programmi che trasformano variabili casuali utilizzando funzioni biunivoche (es jnp.exp , jnp.tanh , jnp.split ).

def log_normal(key):
  return 2 * jnp.exp(random_variable(tfd.Normal(0., 1.))(key))
print(log_prob(log_normal)(1.))

-1.159165

Al fine di calcolare un campione da log_normal 's log-densità, in primo luogo abbiamo bisogno di invertire exp , prendendo il log del campione, e quindi aggiungere una correzione del volume cambiamento utilizzando il registro-det inversa Jacobiano di exp (vedere il cambiamento variabile formula da Wikipedia).

1. log_prob opere con programmi che le strutture di uscita dei campioni piace, dizionari Python o tuple.

def normal_2d(key):
  x = random_variable(
    tfd.MultivariateNormalDiag(jnp.zeros(2), jnp.ones(2)))(key)
  x1, x2 = jnp.split(x, 2, 0)
  return dict(x1=x1, x2=x2)
sample = normal_2d(random.PRNGKey(0))
print(sample)
print(log_prob(normal_2d)(sample))

{'x1': DeviceArray([-0.7847661], dtype=float32), 'x2': DeviceArray([0.8564447], dtype=float32)}
-2.5125546

1. log_prob cammina il grafico calcolo tracciato della funzione, calcolando valori sia in avanti e inversi (e loro log-det Jacobiani) quando necessario in un tentativo di connessione valori restituiti con i valori campionati di base tramite un cambiamento ben definito di variabili. Prendi il seguente programma di esempio:

def complex_program(key):
  k1, k2 = random.split(key)
  z = random_variable(tfd.Normal(0., 1.))(k1)
  x = random_variable(tfd.Normal(jax.nn.relu(z), 1.))(k2)
  return jnp.exp(z), jax.nn.sigmoid(x)
sample = complex_program(random.PRNGKey(0))
print(sample)
print(log_prob(complex_program)(sample))

(DeviceArray(1.1547576, dtype=float32), DeviceArray(0.24830955, dtype=float32))
-1.0967848

In questo programma, noi campioni x condizionalmente su z , il che significa che abbiamo bisogno del valore di z prima di poter calcolare il registro densità di x . Tuttavia, al fine di calcolare z , dobbiamo prima di invertire il jnp.exp applicata a z . Pertanto, per calcolare i log-densità di x e z , log_prob esigenze al primo invertito la prima uscita, e quindi passare avanti attraverso la jax.nn.relu per calcolare la media di p(x | z) .

Nota: mentre log_prob non funzionerà su programmi che variabili casuali di esempio che non vengono restituiti come uscite, joint_sample possono convertire un programma in quello che fa.

Per ulteriori informazioni su log_prob , è possibile fare riferimento a core.interpreters.log_prob . In attuazione, log_prob si basa strettamente iniziale del inverse trasformazione JAX; per saperne di più su inverse , vedere core.interpreters.inverse .

joint_sample

Per definire programmi più complessi e interessanti, utilizzeremo alcune variabili casuali latenti, cioè variabili casuali con valori non osservati. Facciamo riferimento al latent_normal programma che campiona un valore casuale z che viene utilizzato come mezzo di un altro valore casuale x .

def latent_normal(key):
  z_key, x_key = random.split(key)
  z = random_variable(tfd.Normal(0., 1.), name='z')(z_key)
  return random_variable(tfd.Normal(z, 1e-1), name='x')(x_key)

In questo programma, z è così latente se dovessimo chiamare solo latent_normal(random.PRNGKey(0)) non avremmo conoscere il valore effettivo di z che è responsabile della generazione x .

joint_sample è una trasformazione che trasforma un programma in un altro programma che restituisce un dizionario di nomi di stringa mappatura (tag) ai loro valori. Per funzionare, dobbiamo assicurarci di taggare le variabili latenti per assicurarci che appaiano nell'output della funzione trasformata.

joint_sample(latent_normal)(random.PRNGKey(0))

{'x': DeviceArray(0.01873656, dtype=float32),
 'z': DeviceArray(0.14389044, dtype=float32)}

Si noti che joint_sample trasforma un programma in un altro programma che campiona la distribuzione congiunto, sulle valori latenti, così possiamo trasformare ulteriormente. Per algoritmi come MCMC e VI, è comune calcolare la probabilità logaritmica della distribuzione congiunta come parte della procedura di inferenza. log_prob(latent_normal) non funziona perché richiede emarginando su z , ma possiamo utilizzare log_prob(joint_sample(latent_normal)) .

print(log_prob(joint_sample(latent_normal))(dict(x=0., z=1.)))
print(log_prob(joint_sample(latent_normal))(dict(x=0., z=-10.)))

-50.03529
-5049.535

Poiché questo è un modello così comune, Orice ha anche una joint_log_prob trasformazione che è solo la composizione di log_prob e joint_sample .

print(joint_log_prob(latent_normal)(dict(x=0., z=1.)))
print(joint_log_prob(latent_normal)(dict(x=0., z=-10.)))

-50.03529
-5049.535

block

Il block trasformazione avviene in un programma ed una sequenza di nomi e restituisce un programma che si comporta in modo identico eccetto che nelle trasformazioni a valle (come joint_sample ), i nomi forniti vengono ignorati. Un esempio in cui block è utile è la conversione di una distribuzione congiunta in una prima sulle variabili latenti "blocco" i valori campionati della probabilità. Ad esempio, prendere latent_normal , che prima disegna una z ~ N(0, 1) poi una x | z ~ N(z, 1e-1) . block(latent_normal, names=['x']) è un programma che nasconde il x nome, quindi se facciamo joint_sample(block(latent_normal, names=['x'])) , si ottiene un dizionario con solo z in esso .

blocked = block(latent_normal, names=['x'])
joint_sample(blocked)(random.PRNGKey(0))

{'z': DeviceArray(0.14389044, dtype=float32)}

intervene

Il intervene trasformazione clobbers campioni in un programma probabilistico con valori dall'esterno. Tornando al nostro latent_normal programma, diciamo che erano interessati a correre lo stesso programma ma ha voluto z da fissare a 4. Piuttosto che scrivere un nuovo programma, possiamo usare intervene per sostituire il valore di z .

intervened = intervene(latent_normal, z=4.)
sns.distplot(vmap(intervened)(random.split(random.PRNGKey(0), 10000)))
plt.show();

/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

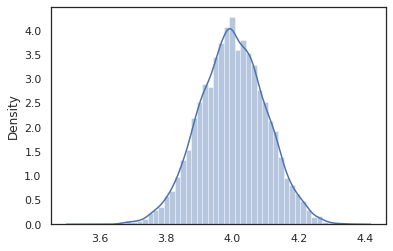
I intervened campioni funzione di p(x | do(z = 4)) che è solo una distribuzione normale standard centrata a 4. Quando si intervene su un valore particolare, tale valore non è più considerato una variabile casuale. Ciò significa che un z valore non verranno contrassegnate durante l'esecuzione intervened .

conditional

conditional trasforma un programma che i campioni latenti valori in uno che condizioni tali valori latenti. Tornando al nostro latent_normal programma, che i campioni p(x) con una latente z , possiamo convertirlo in un programma condizionale p(x | z) .

cond_program = conditional(latent_normal, 'z')
print(cond_program(random.PRNGKey(0), 100.))
print(cond_program(random.PRNGKey(0), 50.))
sns.distplot(vmap(lambda key: cond_program(key, 1.))(random.split(random.PRNGKey(0), 10000)))
sns.distplot(vmap(lambda key: cond_program(key, 2.))(random.split(random.PRNGKey(0), 10000)))
plt.show()

99.87485
49.874847
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)
/home/kbuilder/.local/lib/python3.6/site-packages/seaborn/distributions.py:2551: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
  warnings.warn(msg, FutureWarning)

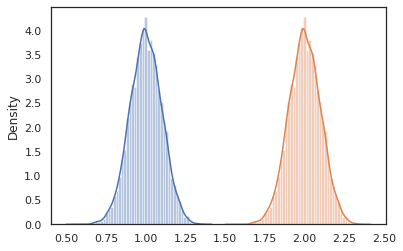
nest

Quando iniziamo a comporre programmi probabilistici per costruirne di più complessi, è comune riutilizzare funzioni che hanno una logica importante. Ad esempio, se ci piacerebbe costruire una rete neurale bayesiana, ci potrebbe essere un importante dense programma che campioni pesi e esegue un passaggio in avanti.

Se riutilizziamo funzioni, tuttavia, potremmo finire con i valori con tag duplicati nel programma definitivo, che viene annullato da trasformazioni come joint_sample . Possiamo usare il nest per creare tag "Scopes" in cui verranno inseriti in un dizionario nidificato eventuali campioni all'interno di un ambito di nome.

def f(key):
  return random_variable(tfd.Normal(0., 1.), name='x')(key)

def g(key):
  k1, k2 = random.split(key)
  return nest(f, scope='x1')(k1) + nest(f, scope='x2')(k2)
joint_sample(g)(random.PRNGKey(0))

{'x1': {'x': DeviceArray(0.14389044, dtype=float32)},
 'x2': {'x': DeviceArray(-1.2515389, dtype=float32)} }

Caso di studio: rete neurale bayesiana

Proviamo la nostra mano a formare una rete neurale bayesiana per classificare il classico Fisher Iris set di dati. È relativamente piccolo e di dimensioni ridotte, quindi possiamo provare a campionare direttamente il posteriore con MCMC.

Per prima cosa, importiamo il set di dati e alcune utilità aggiuntive da Oryx.

from sklearn import datasets
iris = datasets.load_iris()
features, labels = iris['data'], iris['target']

num_features = features.shape[-1]
num_classes = len(iris.target_names)

from oryx.experimental import mcmc
from oryx.util import summary, get_summaries

Iniziamo implementando uno strato denso, che avrà normali precedenti sui pesi e sul bias. Per fare questo, prima si definisce una dense funzione di ordine superiore che porta nella funzione dimensione di uscita e l'attivazione desiderato. La dense funzione restituisce un programma probabilistica che rappresenta una distribuzione condizionata p(h | x) dove h è l'uscita di uno strato denso e x è il suo ingresso. It primi campioni del peso e polarizzazione e poi li applica a x .

def dense(dim_out, activation=jax.nn.relu):
  def forward(key, x):
    dim_in = x.shape[-1]
    w_key, b_key = random.split(key)
    w = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out, dim_in)),
          name='w')(w_key)
    b = random_variable(
          tfd.Sample(tfd.Normal(0., 1.), sample_shape=(dim_out,)),
          name='b')(b_key)
    return activation(jnp.dot(w, x) + b)
  return forward

Per comporre diversi dense strati insieme, implementeremo un mlp funzione di ordine superiore (multistrato percettrone) che tiene in un elenco di dimensioni nascoste e un numero di classi. Esso restituisce un programma che chiama ripetutamente dense usando l'apposito hidden_size e, infine, restituisce logit per ogni classe nel livello finale. Si noti l'uso del nest che crea nome scopi per ogni strato.

def mlp(hidden_sizes, num_classes):
  num_hidden = len(hidden_sizes)
  def forward(key, x):
    keys = random.split(key, num_hidden + 1)
    for i, (subkey, hidden_size) in enumerate(zip(keys[:-1], hidden_sizes)):
      x = nest(dense(hidden_size), scope=f'layer_{i + 1}')(subkey, x)
    logits = nest(dense(num_classes, activation=lambda x: x),
                  scope=f'layer_{num_hidden + 1}')(keys[-1], x)
    return logits
  return forward

Per implementare il modello completo, avremo bisogno di modellare le etichette come variabili casuali categoriali. Ci definiamo una predict funzione che prende in un set di dati di xs (le caratteristiche) che vengono poi passati in un mlp utilizzando vmap . Quando usiamo vmap(partial(mlp, mlp_key)) , campioniamo un unico insieme di pesi, ma mappare il passo in avanti su tutti gli ingressi xs . Questo produce un insieme di logits che parametrizza distribuzioni categoriali indipendenti.

def predict(mlp):
  def forward(key, xs):
    mlp_key, label_key = random.split(key)
    logits = vmap(partial(mlp, mlp_key))(xs)
    return random_variable(
        tfd.Independent(tfd.Categorical(logits=logits), 1), name='y')(label_key)
  return forward

Questo è il modello completo! Usiamo MCMC per campionare il posteriore dei pesi BNN dati dati; prima costruiamo un BNN "template" utilizzando mlp .

bnn = mlp([200, 200], num_classes)

Per costruire un punto di partenza per la nostra catena Markov, possiamo usare joint_sample con un ingresso manichino.

weights = joint_sample(bnn)(random.PRNGKey(0), jnp.ones(num_features))
print(weights.keys())

dict_keys(['layer_1', 'layer_2', 'layer_3'])

Il calcolo della probabilità logaritmica della distribuzione congiunta è sufficiente per molti algoritmi di inferenza. Vediamo ora dicono che osserviamo x e vogliamo assaggiare posteriore p(z | x) . Per le distribuzioni complesse, non saremo in grado di marginalizzare su x (se per latent_normal possiamo) ma possiamo calcolare una densità non normalizzata log log p(z, x) dove x è fissato ad un valore particolare. Possiamo usare la probabilità logaritmica non normalizzata con MCMC per campionare il posteriore. Scriviamo questa funzione log prob "bloccata".

def target_log_prob(weights):
  return joint_log_prob(predict(bnn))(dict(weights, y=labels), features)

Ora possiamo usare tfp.mcmc per assaggiare posteriore usando la nostra funzione di densità di registro non normalizzato. Si noti che dovremo utilizzare una versione "appiattita" dei nostri pesi nidificate dizionario per essere compatibile con tfp.mcmc , in modo da utilizzare le utilità albero di JAX per appiattire e unflatten.

@jit
def run_chain(key, weights):
  flat_state, sample_tree = jax.tree_flatten(weights)

  def flat_log_prob(*states):
    return target_log_prob(jax.tree_unflatten(sample_tree, states))

  def trace_fn(_, results):
    return results.inner_results.accepted_results.target_log_prob

  flat_states, log_probs = tfp.mcmc.sample_chain(
    1000,
    num_burnin_steps=9000,
    kernel=tfp.mcmc.DualAveragingStepSizeAdaptation(
        tfp.mcmc.HamiltonianMonteCarlo(flat_log_prob, 1e-3, 100),
        9000, target_accept_prob=0.7),
    trace_fn=trace_fn,
    current_state=flat_state,
    seed=key)
  samples = jax.tree_unflatten(sample_tree, flat_states)
  return samples, log_probs
posterior_weights, log_probs = run_chain(random.PRNGKey(0), weights)

plt.plot(log_probs)
plt.show()

Possiamo utilizzare i nostri campioni per ottenere una stima della media del modello bayesiano (BMA) dell'accuratezza dell'addestramento. Per calcolare, possiamo usare intervene con bnn a "iniezione" posteriore pesi al posto di quelli che vengono campionati dalla chiave. Per calcolare logit per ogni punto di dati per ogni campione posteriori, possiamo raddoppiare vmap oltre posterior_weights e features .

output_logits = vmap(lambda weights: vmap(lambda x: intervene(bnn, **weights)(
    random.PRNGKey(0), x))(features))(posterior_weights)
output_probs = jax.nn.softmax(output_logits)

print('Average sample accuracy:', (
    output_probs.argmax(axis=-1) == labels[None]).mean())
print('BMA accuracy:', (
    output_probs.mean(axis=0).argmax(axis=-1) == labels[None]).mean())

Average sample accuracy: 0.9874067
BMA accuracy: 0.99333334

Conclusione

In Oryx, i programmi probabilistici sono solo funzioni JAX che accettano la (pseudo)casualità come input. Grazie alla stretta integrazione di Oryx con il sistema di trasformazione delle funzioni di JAX, possiamo scrivere e manipolare programmi probabilistici come se stessimo scrivendo codice JAX. Ciò si traduce in un sistema semplice ma flessibile per costruire modelli complessi e fare inferenze.