আরএল এবং ডিপ কিউ নেটওয়ার্কের পরিচিতি

TensorFlow.org এ দেখুন Google Colab-এ চালান GitHub-এ উৎস দেখুন নোটবুক ডাউনলোড করুন

ভূমিকা

রিইনফোর্সমেন্ট লার্নিং (RL) হল একটি সাধারণ কাঠামো যেখানে এজেন্টরা একটি পরিবেশে কর্ম সম্পাদন করতে শেখে যাতে একটি পুরস্কার সর্বাধিক করা যায়। দুটি প্রধান উপাদান হল পরিবেশ, যা সমাধানের জন্য সমস্যার প্রতিনিধিত্ব করে এবং এজেন্ট, যা শেখার অ্যালগরিদমকে প্রতিনিধিত্ব করে।

এজেন্ট এবং পরিবেশ ক্রমাগত একে অপরের সাথে যোগাযোগ করে। প্রতিটি সময় ধাপে, প্রতিনিধি নীতি উপর ভিত্তি করে পরিবেশ উপর ক্রিয়া লাগে \(\pi(a_t|s_t)\), যেখানে \(s_t\) পরিবেশ থেকে বর্তমান পর্যবেক্ষণ, এবং একটি পুরস্কার পায় \(r_{t+1}\) এবং পরবর্তী পর্যবেক্ষণ \(s_{t+1}\) পরিবেশ থেকে . লক্ষ্য হল নীতির উন্নতি করা যাতে পুরষ্কারের যোগফল (রিটার্ন) সর্বাধিক করা যায়।

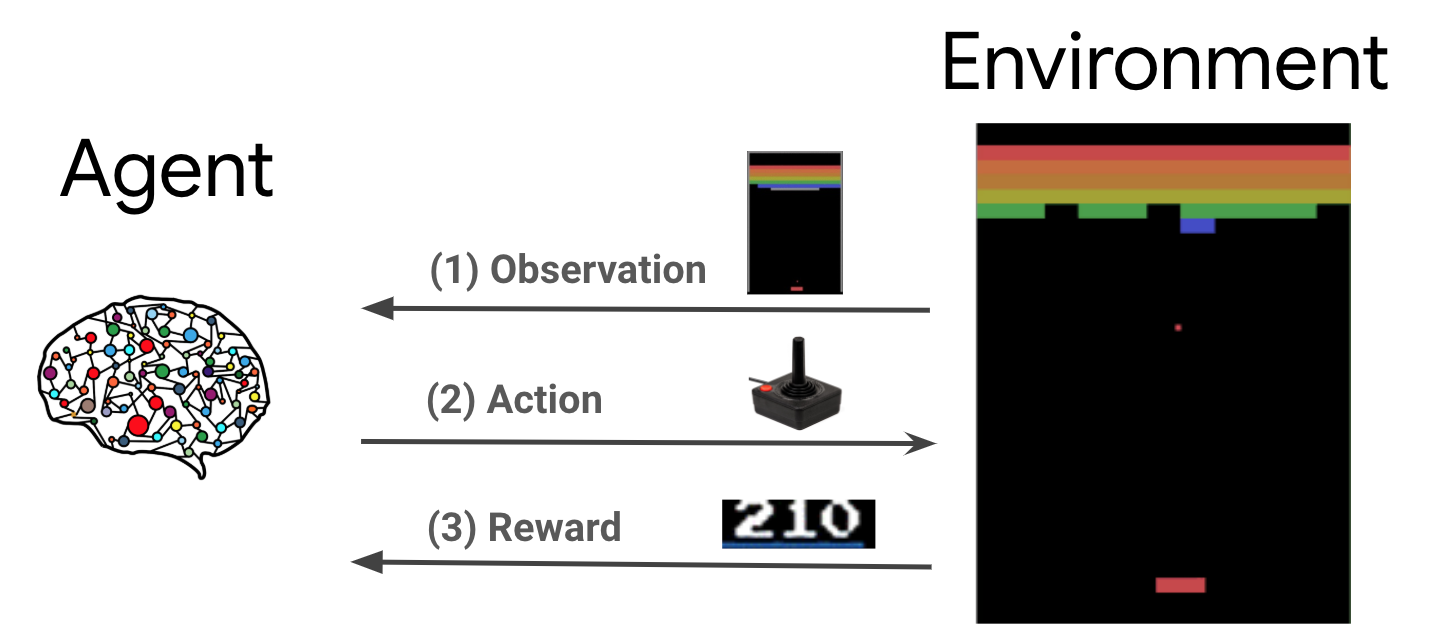
এজেন্ট-এনভায়রনমেন্ট ইন্টারেশান লুপ

এটি একটি খুব সাধারণ ফ্রেমওয়ার্ক এবং গেম, রোবোটিক্স ইত্যাদির মতো বিভিন্ন ক্রমিক সিদ্ধান্ত গ্রহণের সমস্যাগুলির মডেল করতে পারে।

কার্টপোল পরিবেশ

Cartpole পরিবেশ সবচেয়ে সুপরিচিত ক্লাসিক শক্তিবৃদ্ধি শেখার সমস্যার এক (আরএল এর "হ্যালো, বিশ্ব!") হয়। একটি খুঁটি একটি কার্টের সাথে সংযুক্ত, যা একটি ঘর্ষণহীন ট্র্যাক বরাবর চলতে পারে। মেরুটি সোজা শুরু হয় এবং লক্ষ্য হল কার্ট নিয়ন্ত্রণ করে এটিকে পড়া থেকে রোধ করা।

  • পরিবেশ থেকে পর্যবেক্ষণ \(s_t\) অবস্থান এবং কার্ট বেগ এবং কোণ এবং মেরু কৌণিক বেগ প্রতিনিধিত্বমূলক একটি 4D বাহক।
  • এজেন্ট 2 ক্রিয়ার মধ্যে একটি গ্রহণ করে সিস্টেম নিয়ন্ত্রণ করতে পারেন \(a_t\): ধাক্কা কার্ট অধিকার (+1 টি) অথবা বামে (-1)।
  • একটি পুরস্কার \(r_{t+1} = 1\) প্রত্যেক timestep যে মেরু ন্যায়পরায়ণ অবশেষ জন্য প্রদান করা হয়। নিম্নলিখিতগুলির একটি সত্য হলে পর্বটি শেষ হয়:
    • কিছু কোণ সীমা উপর মেরু টিপস
    • কার্টটি বিশ্বের প্রান্তের বাইরে চলে যায়
    • 200 সময় ধাপ পাস.

এজেন্ট লক্ষ্য একটি নীতি শিখতে \(\pi(a_t|s_t)\) তাই হিসাবে একটি পর্বের পুরস্কার এর সমষ্টি বাড়ানোর লক্ষ্যে \(\sum_{t=0}^{T} \gamma^t r_t\)। এখানে \(\gamma\) একটি ডিসকাউন্ট ফ্যাক্টর \([0, 1]\) যে ডিসকাউন্ট ভবিষ্যৎ অবিলম্বে পুরষ্কার আপেক্ষিক প্রতিদান দিয়ে থাকেন। এই প্যারামিটারটি আমাদের নীতিতে ফোকাস করতে সাহায্য করে, এটি দ্রুত পুরষ্কার পাওয়ার বিষয়ে আরও যত্নশীল করে তোলে।

ডিকিউএন এজেন্ট

DQN (গভীর কিউ-নেটওয়ার্ক) অ্যালগরিদম 2015. DeepMind দ্বারা উন্নত ছিল এটা মাত্রায় শক্তিবৃদ্ধি শেখার এবং গভীর স্নায়ুর নেটওয়ার্ক মিশ্রন দ্বারা Atari -এ গেম বিস্তৃত (অতিমানবীয় স্তর কিছু) সমাধান করতে সক্ষম হন। অ্যালগরিদম গভীর নিউরাল নেটওয়ার্ক এবং একটি কৌশল নামক অভিজ্ঞতা রিপ্লে সঙ্গে কিউ-লার্নিং নামক একটি ক্লাসিক আরএল অ্যালগরিদম বৃদ্ধিকারী দ্বারা উন্নত ছিল।

প্রশ্ন-শিক্ষা

Q-লার্নিং একটি Q-ফাংশনের ধারণার উপর ভিত্তি করে। একটি নীতির প্রশ্ন ফাংশনের (ওরফে রাষ্ট্রীয় কর্ম মান ফাংশন) \(\pi\), \(Q^{\pi}(s, a)\), পরিমাপ প্রত্যাশিত রিটার্ন বা ছাড় সমষ্টি রাষ্ট্র থেকে প্রাপ্ত পুরস্কারের \(s\) ব্যবস্থা গ্রহণের দ্বারা \(a\) প্রথম ও নীতি অনুসরণ \(\pi\) তারপরে। আমরা অনুকূল কিউ-ফাংশন নির্ধারণ \(Q^*(s, a)\) সর্বাধিক রিটার্ন যে পর্যবেক্ষণের থেকে শুরু প্রাপ্ত করা যাবে যেমন \(s\), ব্যবস্থা গ্রহণের \(a\) এবং তারপরে অনুকূল নীতি নিম্নলিখিত। অনুকূল কিউ-ফাংশন আনুগত্য নিম্নলিখিত বেলম্যান optimality সমীকরণ:

\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)

এর অর্থ এই যে রাষ্ট্র থেকে সর্বোচ্চ রিটার্ন \(s\) এবং কর্ম \(a\) তাৎক্ষণিক পুরস্কার এর সমষ্টি \(r\) এবং বিনিময়ে (দ্বারা ছাড় \(\gamma\)) পর্বের শেষ না হওয়া পর্যন্ত তারপরে অনুকূল নীতি অনুসরণ করে প্রাপ্ত ( অর্থাত, পরবর্তী রাষ্ট্র থেকে সর্বোচ্চ পুরস্কার \(s'\))। প্রত্যাশা উভয় অবিলম্বে পুরষ্কার বিতরণের উপর নির্ণয় করা হয় \(r\) এবং সম্ভব পরবর্তী রাজ্যের \(s'\)।

কিউ-লার্নিং পিছনে মৌলিক ধারণা একটি পুনরাবৃত্ত আপডেট হিসাবে বেলম্যান optimality সমীকরণ ব্যবহার করা \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\), এবং এটি দেখানো যেতে পারে যে অনুকূল এই এগোয় \(Q\)-function, অর্থাত্ \(Q_i \rightarrow Q^*\) যেমন \(i \rightarrow \infty\) (দেখুন DQN কাগজ )।

গভীর Q-শিক্ষা

প্রায় সকল সমস্যার জন্য, এটি প্রতিনিধিত্ব করতে অকার্যকর হয় \(Q\)প্রতিটি সংযুক্তির জন্য মান ধারণকারী একটি টেবিল হিসাবে -function \(s\) এবং \(a\)। এর পরিবর্তে, আমরা এই ধরনের পরামিতি সঙ্গে একটি স্নায়ুর নেটওয়ার্ক যেমন একটি ফাংশন approximator প্রশিক্ষণ, \(\theta\)কিউ-মূল্যবোধ, অর্থাত অনুমান করার জন্য \(Q(s, a; \theta) \approx Q^*(s, a)\)। এই প্রতিটি পদক্ষেপ নিম্নলিখিত ক্ষতি কমানোর দ্বারা সম্পন্ন করতে \(i\):

\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) যেখানে \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)

এখানে, \(y_i\) : TD (সময়গত পার্থক্য) লক্ষ্য বলা হয়, এবং \(y_i - Q\) : TD ত্রুটি বলা হয়। \(\rho\) আচরণ বন্টন, ট্রানজিশন উপর বন্টন প্রতিনিধিত্ব করে \(\{s, a, r, s'\}\) পরিবেশ থেকে সংগ্রহ করেছিলেন।

নোট যে আগের পুনরাবৃত্তির থেকে পরামিতি \(\theta_{i-1}\) ঠিক করা হয়েছে এবং আপডেট না। অনুশীলনে আমরা শেষ পুনরাবৃত্তির পরিবর্তে কয়েকটি পুনরাবৃত্তি আগে থেকে নেটওয়ার্ক প্যারামিটারের একটি স্ন্যাপশট ব্যবহার করি। এই অনুলিপিটি লক্ষ্য নেটওয়ার্কের বলা হয়।

কিউ-লার্নিং একটি অফ-নীতি অ্যালগরিদম যে লোভী নীতি সম্বন্ধে শেখে হয় \(a = \max_{a} Q(s, a; \theta)\) / পরিবেশে অভিনয় তথ্য সংগ্রহের জন্য একটি আলাদা আচরণ নীতি ব্যবহার করে না। এই আচরণ নীতি সাধারণত একটি হল \(\epsilon\)-greedy নীতি নির্বাচন সম্ভাব্যতা সঙ্গে লোভী কর্ম \(1-\epsilon\) এবং সম্ভাব্যতা সঙ্গে একটি র্যান্ডম কর্ম \(\epsilon\) রাষ্ট্রীয় কর্ম স্থান ভাল কভারেজ নিশ্চিত করতে হবে।

অভিজ্ঞতা রিপ্লে

DQN ক্ষতির সম্পূর্ণ প্রত্যাশা গণনা এড়াতে, আমরা স্টোকাস্টিক গ্রেডিয়েন্ট ডিসেন্ট ব্যবহার করে এটি কমিয়ে আনতে পারি। ক্ষয় মাত্র গত রূপান্তরটি ব্যবহার করে গণনা করা হয়, তাহলে \(\{s, a, r, s'\}\), এই মান কিউ-শেখার হ্রাস করা হয়।

Atari DQN কাজ নেটওয়ার্ক আপডেটগুলিকে আরও স্থিতিশীল করতে এক্সপেরিয়েন্স রিপ্লে নামে একটি কৌশল চালু করেছে। সংগৃহীত ডাটা প্রতিটি সময় ধাপ অনুযায়ী, ট্রানজিশন একটি বৃত্তাকার বাফার রিপ্লে বাফার নামক যোগ করা হয়। তারপরে প্রশিক্ষণের সময়, ক্ষতি এবং এর গ্রেডিয়েন্ট গণনা করার জন্য কেবলমাত্র সর্বশেষ রূপান্তর ব্যবহার করার পরিবর্তে, আমরা রিপ্লে বাফার থেকে নমুনাকৃত রূপান্তরের একটি মিনি-ব্যাচ ব্যবহার করে তাদের গণনা করি। এর দুটি সুবিধা রয়েছে: অনেকগুলি আপডেটে প্রতিটি ট্রানজিশন পুনঃব্যবহার করে আরও ভাল ডেটা দক্ষতা এবং একটি ব্যাচে অসম্পর্কিত রূপান্তর ব্যবহার করে আরও ভাল স্থিতিশীলতা।

TF-এজেন্টে কার্টপোলে DQN

TF-Agents একটি DQN এজেন্টকে প্রশিক্ষণ দেওয়ার জন্য প্রয়োজনীয় সমস্ত উপাদান প্রদান করে, যেমন এজেন্ট নিজেই, পরিবেশ, নীতি, নেটওয়ার্ক, রিপ্লে বাফার, ডেটা সংগ্রহের লুপ এবং মেট্রিক্স। এই উপাদানগুলি পাইথন ফাংশন বা টেনসরফ্লো গ্রাফ অপস হিসাবে প্রয়োগ করা হয় এবং আমাদের কাছে তাদের মধ্যে রূপান্তর করার জন্য মোড়ক রয়েছে। উপরন্তু, TF-Agents TensorFlow 2.0 মোড সমর্থন করে, যা আমাদেরকে প্রয়োজনীয় মোডে TF ব্যবহার করতে সক্ষম করে।

এর পরে, কটাক্ষপাত করা মেমরি-এজেন্ট ব্যবহার Cartpole পরিবেশের ওপর DQN এজেন্ট প্রশিক্ষণ জন্য টিউটোরিয়াল ।