ลิขสิทธิ์ 2021 The TF-Agents Authors.
 ดูบน TensorFlow.org ดูบน TensorFlow.org |  ทำงานใน Google Colab ทำงานใน Google Colab |  ดูแหล่งที่มาบน GitHub ดูแหล่งที่มาบน GitHub |  ดาวน์โหลดโน๊ตบุ๊ค ดาวน์โหลดโน๊ตบุ๊ค |
บทนำ
การเรียนรู้การเสริมแรง (RL) เป็นกรอบการทำงานทั่วไปที่ตัวแทนเรียนรู้ที่จะดำเนินการในสภาพแวดล้อมเพื่อให้ได้รางวัลสูงสุด องค์ประกอบหลักสองอย่างคือ สภาพแวดล้อม ซึ่งแสดงถึงปัญหาที่จะแก้ไข และตัวแทน ซึ่งแสดงถึงอัลกอริธึมการเรียนรู้
ตัวแทนและสิ่งแวดล้อมมีปฏิสัมพันธ์ซึ่งกันและกันอย่างต่อเนื่อง ในแต่ละขั้นตอนเวลาที่ตัวแทนจะใช้เวลาดำเนินการในสภาพแวดล้อมที่อยู่บนพื้นฐานของนโยบาย \(\pi(a_t|s_t)\)ที่ \(s_t\) เป็นข้อสังเกตในปัจจุบันจากสภาพแวดล้อมและได้รับรางวัล \(r_{t+1}\) และสังเกตต่อไป \(s_{t+1}\) จากสภาพแวดล้อม . เป้าหมายคือการปรับปรุงนโยบายเพื่อให้ได้ผลตอบแทนสูงสุด (ผลตอบแทน) สูงสุด
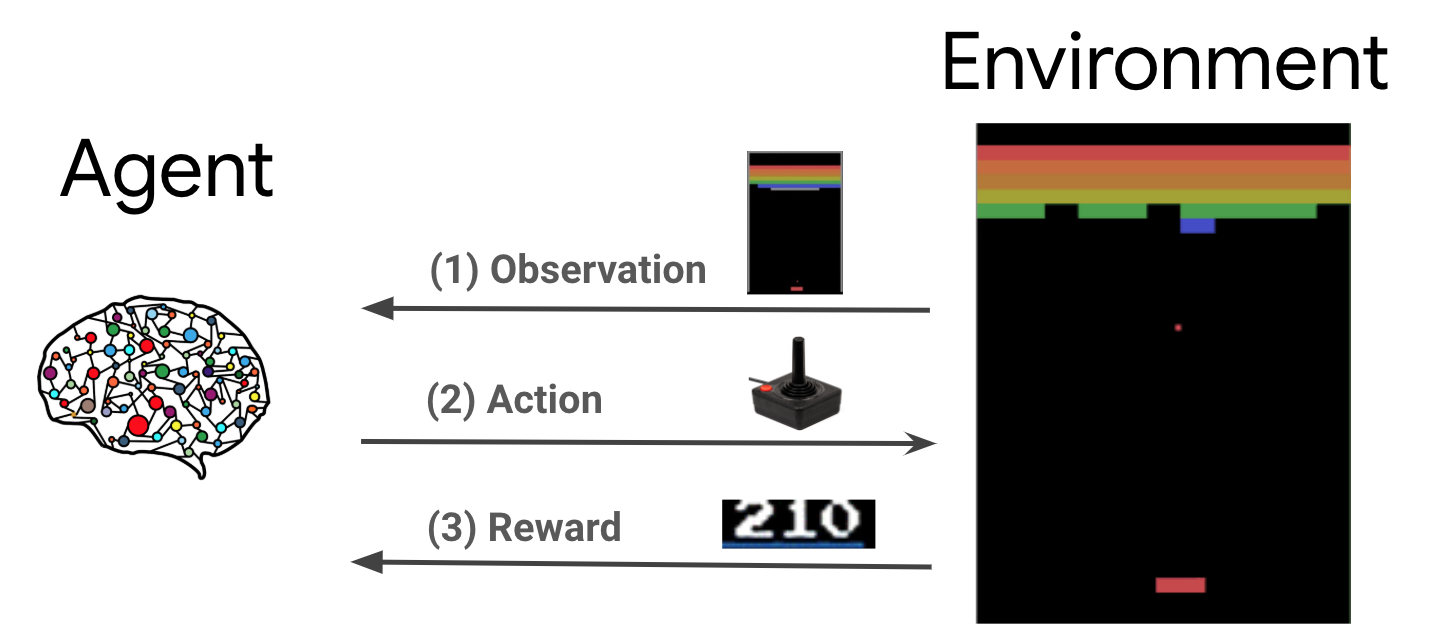
นี่เป็นกรอบงานทั่วไป และสามารถจำลองปัญหาการตัดสินใจตามลำดับได้หลากหลาย เช่น เกม วิทยาการหุ่นยนต์ เป็นต้น
สิ่งแวดล้อม Cartpole
สภาพแวดล้อม Cartpole เป็นหนึ่งในที่รู้จักกันดีที่สุดปัญหาการเรียนรู้การเสริมแรงคลาสสิก ( "Hello World!" ของ RL) เสาติดอยู่กับเกวียนซึ่งสามารถเคลื่อนที่ไปตามรางที่ไม่มีการเสียดสี เสาเริ่มตั้งตรงและมีเป้าหมายเพื่อป้องกันไม่ให้ล้มโดยการควบคุมรถเข็น
- สังเกตจากสภาพแวดล้อม \(s_t\) เป็นเวกเตอร์ 4D เป็นตัวแทนของตำแหน่งและความเร็วของรถเข็นและมุมและความเร็วเชิงมุมของเสา
- ตัวแทนสามารถควบคุมระบบโดยการหนึ่งของการดำเนินการ 2 \(a_t\): ผลักดันรถเข็นขวา (+1) หรือซ้าย (-1)
- รางวัล \(r_{t+1} = 1\) มีให้สำหรับทุก timestep ที่เสายังคงตรง ตอนจะสิ้นสุดลงเมื่อข้อใดข้อหนึ่งต่อไปนี้เป็นจริง:
- ปลายขั้วเหนือขีด จำกัด บางมุม
- เกวียนเคลื่อนออกนอกขอบโลก
- 200 ก้าวผ่านไป
เป้าหมายของตัวแทนคือการเรียนรู้นโยบาย \(\pi(a_t|s_t)\) เพื่อเพิ่มผลรวมของผลตอบแทนในตอน \(\sum_{t=0}^{T} \gamma^t r_t\)นี่ \(\gamma\) เป็นปัจจัยราคาถูกใน \([0, 1]\) ว่าส่วนลดในอนาคตผลตอบแทนเมื่อเทียบกับผลตอบแทนทันที พารามิเตอร์นี้ช่วยให้เรามุ่งเน้นนโยบาย ทำให้ให้ความสำคัญกับการได้รับรางวัลอย่างรวดเร็วมากขึ้น
ตัวแทน DQN
อัลกอริทึม (Deep Q-Network) DQN รับการพัฒนาโดย DeepMind ในปี 2015 มันก็สามารถที่จะแก้ปัญหาที่หลากหลายของเกมอาตาริ (บางคนให้อยู่ในระดับเหนือมนุษย์) โดยการรวมการเรียนรู้การเสริมแรงและเครือข่ายประสาทลึกในระดับ อัลกอริทึมได้รับการพัฒนาโดยการเสริมสร้างอัลกอริทึม RL คลาสสิกที่เรียกว่า Q-การเรียนรู้กับเครือข่ายประสาทลึกและเทคนิคที่เรียกว่ารีเพลย์ประสบการณ์
Q-การเรียนรู้
Q-Learning ขึ้นอยู่กับแนวคิดของฟังก์ชัน Q Q-ฟังก์ชั่น (aka ฟังก์ชั่นคุ้มค่าของรัฐกระทำ) ของนโยบาย \(\pi\), \(Q^{\pi}(s, a)\)มาตรการตอบแทนที่คาดหวังหรือผลรวมที่ลดจากผลตอบแทนที่ได้รับจากรัฐ \(s\) โดยการดำเนินการ \(a\) แรกและต่อไปนี้นโยบาย \(\pi\) หลังจากนั้น เรากำหนดที่ดีที่สุด Q-ฟังก์ชั่น \(Q^*(s, a)\) เป็นผลตอบแทนสูงสุดที่สามารถรับได้เริ่มต้นจากการสังเกต \(s\), การดำเนินการ \(a\) และทำตามนโยบายที่ดีที่สุดหลังจากนั้น อัตราส่วน Q-ฟังก์ชั่นเชื่อฟังสม optimality ยามต่อไปนี้:
\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)
ซึ่งหมายความว่าผลตอบแทนสูงสุดจากรัฐ \(s\) และการกระทำ \(a\) คือผลรวมของรางวัลทันที \(r\) และผลตอบแทน (ลดด้วย \(\gamma\)) ที่ได้จากการปฏิบัติตามนโยบายที่ดีที่สุดหลังจากนั้นจนจบตอนที่ ( คือรางวัลสูงสุดจากรัฐต่อไป \(s'\)) ความคาดหวังคือการคำนวณทั้งกระจายของรางวัลทันที \(r\) และรัฐต่อไปเป็นไปได้ \(s'\)
ความคิดพื้นฐานหลัง Q-การเรียนรู้คือการใช้สมการ optimality ยามเป็นการปรับปรุงซ้ำ \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\)และก็สามารถที่จะแสดงให้เห็นว่าลู่นี้ไปยังที่ดีที่สุด \(Q\)ฟังก์ชั่คือ \(Q_i \rightarrow Q^*\) เป็น \(i \rightarrow \infty\) (ดู DQN กระดาษ )
การเรียนรู้ Q ลึก
สำหรับปัญหาส่วนใหญ่ก็จะทำไม่ได้จะเป็นตัวแทนของ \(Q\)ฟังก์ชั่เป็นตารางที่มีค่าสำหรับการรวมกันของแต่ละ \(s\) และ \(a\)แต่เราฝึก approximator ฟังก์ชั่นเช่นเครือข่ายประสาทกับพารามิเตอร์ \(\theta\)เพื่อประเมิน Q-ค่าเช่น \(Q(s, a; \theta) \approx Q^*(s, a)\)นี้สามารถทำได้โดยการลดการสูญเสียต่อไปในแต่ละขั้นตอน \(i\):
\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) ที่ \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)
นี่ \(y_i\) เรียกว่า TD (ความแตกต่างชั่วคราว) เป้าหมายและ \(y_i - Q\) เรียกว่าข้อผิดพลาดการ TD \(\rho\) หมายถึงการกระจายพฤติกรรมการจัดจำหน่ายในช่วงการเปลี่ยน \(\{s, a, r, s'\}\) เก็บรวบรวมจากสภาพแวดล้อม
โปรดทราบว่าพารามิเตอร์จากการย้ำก่อนหน้า \(\theta_{i-1}\) จะคงอยู่และไม่ได้ปรับปรุง ในทางปฏิบัติ เราใช้สแนปชอตของพารามิเตอร์เครือข่ายจากการวนซ้ำหลายครั้งที่ผ่านมา แทนที่จะใช้การวนซ้ำครั้งล่าสุด สำเนานี้เรียกว่าเครือข่ายเป้าหมาย
Q-การเรียนรู้เป็นขั้นตอนวิธีการออกนโยบายที่เรียนรู้เกี่ยวกับนโยบายโลภ \(a = \max_{a} Q(s, a; \theta)\) ในขณะที่ใช้นโยบายพฤติกรรมที่แตกต่างกันสำหรับการทำหน้าที่ในสภาพแวดล้อม / การเก็บรวบรวมข้อมูล นโยบายนี้เป็นพฤติกรรมปกติ \(\epsilon\)นโยบาย -greedy ที่เลือกการกระทำโลภกับความน่าจะ \(1-\epsilon\) และการกระทำที่สุ่มที่มีความน่าจะเป็น \(\epsilon\) เพื่อให้มั่นใจความคุ้มครองที่ดีของพื้นที่ของรัฐดำเนินการ
เล่นซ้ำประสบการณ์
เพื่อหลีกเลี่ยงการคำนวณความคาดหวังทั้งหมดในการสูญเสีย DQN เราสามารถย่อให้เล็กสุดโดยใช้การไล่ระดับสีแบบสุ่ม หากการสูญเสียที่มีการคำนวณโดยใช้เพียงการเปลี่ยนแปลงล่าสุด \(\{s, a, r, s'\}\)นี้จะลดให้เป็นมาตรฐาน Q-Learning
งาน Atari DQN ได้แนะนำเทคนิคที่เรียกว่า Experience Replay เพื่อทำให้การอัปเดตเครือข่ายมีเสถียรภาพมากขึ้น ในแต่ละขั้นตอนเวลาของการเก็บรวบรวมข้อมูลการเปลี่ยนจะมีการเพิ่มกันชนกลมเรียกว่าบัฟเฟอร์รีเพลย์ จากนั้นในระหว่างการฝึกอบรม แทนที่จะใช้เพียงช่วงการเปลี่ยนภาพล่าสุดในการคำนวณการสูญเสียและการไล่ระดับสี เราคำนวณโดยใช้การเปลี่ยนชุดย่อยขนาดเล็กที่สุ่มตัวอย่างจากบัฟเฟอร์การเล่นซ้ำ มีข้อดีสองประการ: ประสิทธิภาพของข้อมูลที่ดีขึ้นโดยการนำการเปลี่ยนแปลงแต่ละครั้งมาใช้ซ้ำในการอัปเดตจำนวนมาก และความเสถียรที่ดีขึ้นโดยใช้การเปลี่ยนที่ไม่สัมพันธ์กันในชุดงาน
DQN บน Cartpole ใน TF-Agents
TF-Agents จัดเตรียมส่วนประกอบทั้งหมดที่จำเป็นในการฝึกเอเจนต์ DQN เช่น เอเจนต์เอง สภาพแวดล้อม นโยบาย เครือข่าย บัฟเฟอร์การเล่นซ้ำ ลูปการรวบรวมข้อมูล และเมทริก ส่วนประกอบเหล่านี้ถูกนำไปใช้เป็นฟังก์ชัน Python หรือ TensorFlow กราฟ ops และเรายังมี wrapper สำหรับการแปลงระหว่างกัน นอกจากนี้ TF-Agents ยังรองรับโหมด TensorFlow 2.0 ซึ่งช่วยให้เราใช้ TF ในโหมดจำเป็นได้
ถัดไปให้ดูที่การ กวดวิชาสำหรับการฝึกอบรมตัวแทน DQN ต่อสิ่งแวดล้อม Cartpole ใช้ตัวแทน TF
