Wprowadzenie do RL i Deep Q Networks

Copyright 2021 Autorzy TF-Agents.

Wstęp

Uczenie się przez wzmacnianie (RL) to ogólna struktura, w której agenci uczą się wykonywać działania w środowisku, aby zmaksymalizować nagrodę. Dwa główne komponenty to środowisko, które reprezentuje problem do rozwiązania, oraz agent, który reprezentuje algorytm uczenia.

Agent i środowisko stale oddziałują na siebie. Na każdym kroku czasowym, agent wykonuje działania na środowisko na podstawie jego polityki \(\pi(a_t|s_t)\), gdzie \(s_t\) jest bieżąca obserwacja ze środowiska, a otrzymuje nagrodę \(r_{t+1}\) i obok obserwacji \(s_{t+1}\) ze środowiska . Celem jest udoskonalenie polityki tak, aby zmaksymalizować sumę nagród (zwrotu).

Uwaga: Ważne jest rozróżnienie między state środowiska i observation , która jest częścią środowiska state , że agent może zobaczyć, na przykład w grze w pokera, stan środowiska składa się z kart należących do wszystkich graczy i karty wspólne, ale agent może obserwować tylko własne karty i kilka kart wspólnych. W większości z literatury wszystkie te określenia stosuje się zamiennie i obserwacja jest również określana jako \(s\).

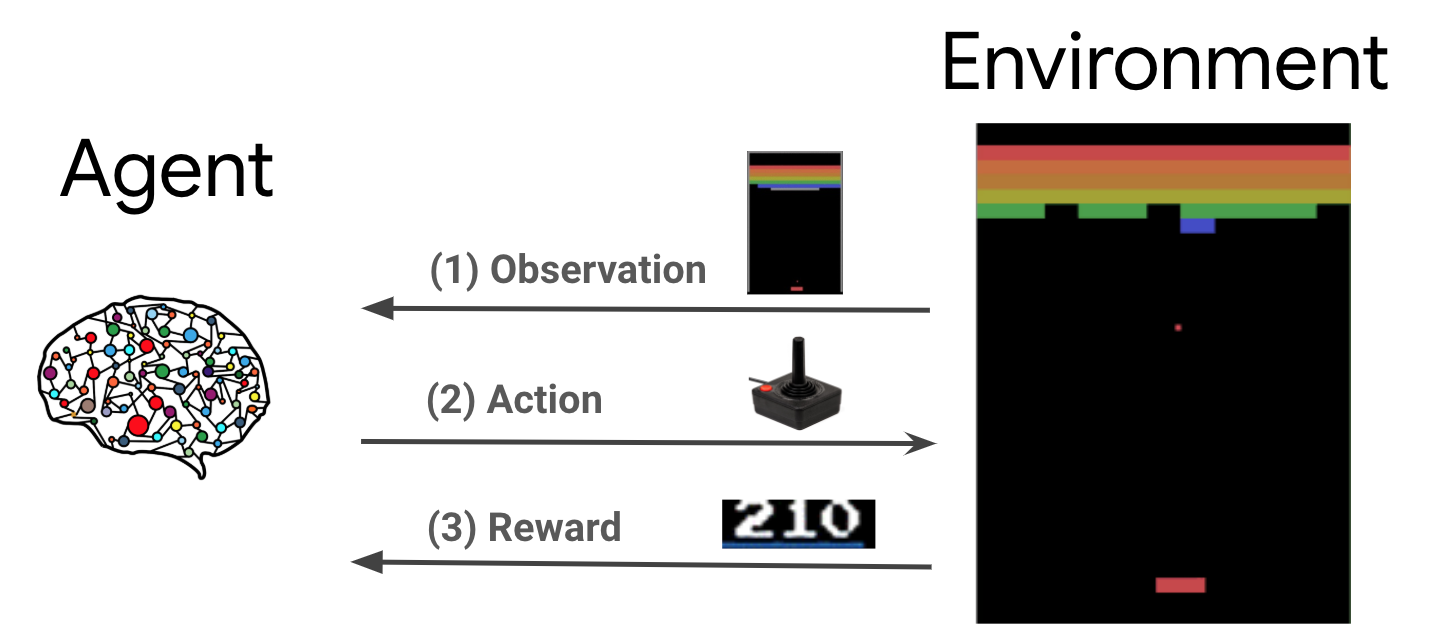
Jest to bardzo ogólna struktura i może modelować różne sekwencyjne problemy związane z podejmowaniem decyzji, takie jak gry, robotyka itp.

Środowisko Cartpole

Środowisko Cartpole jest jednym z najbardziej znanych klasycznych problemów w uczeniu się zbrojenie (dalej „Hello, World!” RL). Do wózka przymocowany jest drążek, który może poruszać się po torze pozbawionym tarcia. Słup zaczyna się pionowo, a celem jest zapobieganie jego przewróceniu poprzez kontrolowanie wózka.

• Obserwacja ze środowiska \(s_t\) jest wektorem 4D reprezentujący położenie i prędkość wózka, a kąt i prędkość kątową bieguna.
• Środek można sterować systemem poprzez podejmowanie działań jednego z 2 \(a_t\): popchnąć wózek prawo (+1) lub w lewo (-1).
• Nagroda \(r_{t+1} = 1\) przewidziano każdym kroku to, że Polak pozostaje w pozycji pionowej. Odcinek kończy się, gdy spełniony jest jeden z poniższych warunków:
  • kij przechyla się powyżej pewnego kąta
  • wózek wyjeżdża poza granice świata
  • Mija 200 kroków czasu.

Celem środka jest nauczyć politykę \(\pi(a_t|s_t)\) tak aby maksymalizować sumę nagród w epizodzie \(\sum_{t=0}^{T} \gamma^t r_t\). Tutaj \(\gamma\) jest czynnikiem zniżki w \([0, 1]\) że rabaty przyszłych nagród w stosunku do natychmiastowych nagród. Ten parametr pomaga nam skoncentrować politykę, sprawiając, że bardziej zależy jej na szybkim zdobywaniu nagród.

Agent DQN

Algorytm DQN (Głębokie Q-Network) została opracowana w 2015 roku przez DeepMind To było w stanie rozwiązać szeroką gamę gier Atari (niektóre na poziomie nadludzkiej) poprzez połączenie nauki zbrojenia i głębokie sieci neuronowych w skali. Algorytm został opracowany przez zwiększanie klasyczny algorytm RL nazwie Q-learning z głębokimi sieci neuronowych i technika zwana doświadczenie powtórki.

Q-Learning

Q-Learning opiera się na pojęciu funkcji Q. Q-function (aka funkcja wartość state-action) z polityki \(\pi\), \(Q^{\pi}(s, a)\)mierzy oczekiwanego zwrotu lub zdyskontowana suma nagród otrzymanych z państwowej \(s\) poprzez podejmowanie działań \(a\) pierwszy i Poniższe zasady \(\pi\) później. Zdefiniować optymalnej funkcji P- \(Q^*(s, a)\) jako powrót maksymalnej, która może zostać uzyskane, począwszy od obserwacji \(s\)biorąc działania \(a\) i zgodnie z polityką optymalne później. Optymalna P funkcja wypełnia następujące równanie optymalność Bellman:

\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)

Oznacza to, że maksymalny zwrot z państwowej \(s\) i działanie \(a\) jest sumą natychmiastowa nagroda \(r\) i powrót (zdyskontowana przez \(\gamma\)) otrzymano zgodnie z polityką optymalną potem do końca odcinka ( czyli maksymalna nagroda od kolejnego państwa \(s'\)). Oczekiwanie jest obliczany zarówno nad dystrybucją natychmiastowych nagród \(r\) i ewentualnych kolejnych stanach \(s'\).

Podstawową ideą Q-learning jest użycie Bellman równania optymalności jako iteracyjny aktualizacji \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\)i można udowodnić, że ten jest zbieżny do optymalnego \(Q\)-function, tj \(Q_i \rightarrow Q^*\) jako \(i \rightarrow \infty\) (patrz DQN papier ).

Głębokie Q-Learning

Dla większości problemów, jest możliwa do reprezentowania \(Q\)-function jako tabeli zawierającej wartości dla każdej kombinacji \(s\) i \(a\). Zamiast tego, możemy trenować Aproksymator funkcji, takich jak sieci neuronowe z parametrami \(\theta\), aby oszacować Q-wartości, tj \(Q(s, a; \theta) \approx Q^*(s, a)\). Można to zrobić poprzez zminimalizowanie następujące straty na każdym kroku \(i\):

\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) gdzie \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)

Tutaj \(y_i\) nazywa TD (różnica czasowa) cel, a \(y_i - Q\) nazywa błąd TD. \(\rho\) przedstawia rozkład zachowaniem, a rozkład na przemian \(\{s, a, r, s'\}\) zebranych z otoczenia.

Należy zauważyć, że parametry z poprzedniej iteracji \(\theta_{i-1}\) są stałe i nie aktualizowane. W praktyce zamiast ostatniej iteracji używamy migawki parametrów sieci sprzed kilku iteracji. Ta kopia jest nazywana siecią docelową.

Q-learning jest algorytmem off-polityka, który dowiaduje się o polityce chciwy \(a = \max_{a} Q(s, a; \theta)\) podczas korzystania inną politykę zachowanie dla działających w środowisku / zbieranie danych. Ta polityka zachowanie jest zwykle \(\epsilon\)-greedy polityka, który wybiera chciwy akcja z prawdopodobieństwem \(1-\epsilon\) i przypadkowej akcji z prawdopodobieństwem \(\epsilon\) aby zapewnić dobre pokrycie przestrzeni state-action.

Przeżyj powtórkę

Aby uniknąć obliczania pełnej wartości oczekiwanej straty DQN, możemy ją zminimalizować za pomocą stochastycznego spadku gradientu. Jeśli ubytek jest obliczany za pomocą tylko ostatniego przejścia \(\{s, a, r, s'\}\), zmniejsza standardowej Q Nauk.

Prace Atari DQN wprowadziły technikę o nazwie Experience Replay, aby uczynić aktualizacje sieci bardziej stabilnymi. Na każdym etapie w czasie zbierania danych, dodawane są do przejścia w buforze cyklicznym zwany bufor do odtwarzania. Następnie podczas treningu, zamiast używać tylko ostatniego przejścia do obliczenia straty i jej gradientu, obliczamy je za pomocą mini-partii przejść próbkowanych z bufora powtórek. Ma to dwie zalety: lepszą wydajność danych dzięki ponownemu wykorzystaniu każdego przejścia w wielu aktualizacjach oraz lepszą stabilność przy użyciu nieskorelowanych przejść w partii.

DQN na Cartpole w TF-Agents

TF-Agents zapewnia wszystkie komponenty niezbędne do szkolenia agenta DQN, takie jak sam agent, środowisko, polityki, sieci, bufory odtwarzania, pętle zbierania danych i metryki. Komponenty te są zaimplementowane jako funkcje Pythona lub operacje wykresów TensorFlow, a także mamy wrappery do konwersji między nimi. Dodatkowo TF-Agents obsługuje tryb TensorFlow 2.0, który umożliwia nam używanie TF w trybie imperatywnym.

Następnie spojrzeć w poradniku do szkolenia agenta DQN na środowisko Cartpole używając TF-Agentów .