View on TensorFlow.org View on TensorFlow.org
|
 Run in Google Colab Run in Google Colab
|
 View source on GitHub View source on GitHub
|
 Download notebook Download notebook
|
In this example we show how to fit regression models using TFP's "probabilistic layers."
Dependencies & Prerequisites
Import
from pprint import pprint
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow as tf
import tf_keras
import tensorflow_probability as tfp
sns.reset_defaults()
#sns.set_style('whitegrid')
#sns.set_context('talk')
sns.set_context(context='talk',font_scale=0.7)
%matplotlib inline
tfd = tfp.distributions
Make things Fast!
Before we dive in, let's make sure we're using a GPU for this demo.
To do this, select "Runtime" -> "Change runtime type" -> "Hardware accelerator" -> "GPU".
The following snippet will verify that we have access to a GPU.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
WARNING: GPU device not found.
Motivation
Wouldn't it be great if we could use TFP to specify a probabilistic model then simply minimize the negative log-likelihood, i.e.,
negloglik = lambda y, rv_y: -rv_y.log_prob(y)
Well not only is it possible, but this colab shows how! (In context of linear regression problems.)
Synthesize dataset.
w0 = 0.125
b0 = 5.
x_range = [-20, 60]
def load_dataset(n=150, n_tst=150):
np.random.seed(43)
def s(x):
g = (x - x_range[0]) / (x_range[1] - x_range[0])
return 3 * (0.25 + g**2.)
x = (x_range[1] - x_range[0]) * np.random.rand(n) + x_range[0]
eps = np.random.randn(n) * s(x)
y = (w0 * x * (1. + np.sin(x)) + b0) + eps
x = x[..., np.newaxis]
x_tst = np.linspace(*x_range, num=n_tst).astype(np.float32)
x_tst = x_tst[..., np.newaxis]
return y, x, x_tst
y, x, x_tst = load_dataset()
Case 1: No Uncertainty
# Build model.
model = tf_keras.Sequential([
tf_keras.layers.Dense(1),
tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])
# Do inference.
model.compile(optimizer=tf_keras.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
0.13032457 5.13029
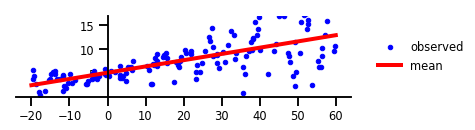
Figure 1: No uncertainty.
w = np.squeeze(model.layers[-2].kernel.numpy())
b = np.squeeze(model.layers[-2].bias.numpy())
plt.figure(figsize=[6, 1.5]) # inches
#plt.figure(figsize=[8, 5]) # inches
plt.plot(x, y, 'b.', label='observed');
plt.plot(x_tst, yhat.mean(),'r', label='mean', linewidth=4);
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig1.png', bbox_inches='tight', dpi=300)
Case 2: Aleatoric Uncertainty
# Build model.
model = tf_keras.Sequential([
tf_keras.layers.Dense(1 + 1),
tfp.layers.DistributionLambda(
lambda t: tfd.Normal(loc=t[..., :1],
scale=1e-3 + tf.math.softplus(0.05 * t[...,1:]))),
])
# Do inference.
model.compile(optimizer=tf_keras.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
[0.14738432 0.1815331 ] [4.4812164 1.2219843]
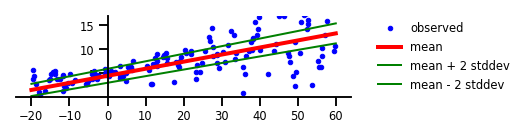
Figure 2: Aleatoric Uncertainty
plt.figure(figsize=[6, 1.5]) # inches
plt.plot(x, y, 'b.', label='observed');
m = yhat.mean()
s = yhat.stddev()
plt.plot(x_tst, m, 'r', linewidth=4, label='mean');
plt.plot(x_tst, m + 2 * s, 'g', linewidth=2, label=r'mean + 2 stddev');
plt.plot(x_tst, m - 2 * s, 'g', linewidth=2, label=r'mean - 2 stddev');
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig2.png', bbox_inches='tight', dpi=300)
Case 3: Epistemic Uncertainty
# Specify the surrogate posterior over `keras.layers.Dense` `kernel` and `bias`.
def posterior_mean_field(kernel_size, bias_size=0, dtype=None):
n = kernel_size + bias_size
c = np.log(np.expm1(1.))
return tf_keras.Sequential([
tfp.layers.VariableLayer(2 * n, dtype=dtype),
tfp.layers.DistributionLambda(lambda t: tfd.Independent(
tfd.Normal(loc=t[..., :n],
scale=1e-5 + tf.nn.softplus(c + t[..., n:])),
reinterpreted_batch_ndims=1)),
])
# Specify the prior over `keras.layers.Dense` `kernel` and `bias`.
def prior_trainable(kernel_size, bias_size=0, dtype=None):
n = kernel_size + bias_size
return tf_keras.Sequential([
tfp.layers.VariableLayer(n, dtype=dtype),
tfp.layers.DistributionLambda(lambda t: tfd.Independent(
tfd.Normal(loc=t, scale=1),
reinterpreted_batch_ndims=1)),
])
# Build model.
model = tf_keras.Sequential([
tfp.layers.DenseVariational(1, posterior_mean_field, prior_trainable, kl_weight=1/x.shape[0]),
tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])
# Do inference.
model.compile(optimizer=tf_keras.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
[ 0.1387333 5.125723 -4.112224 -2.2171402] [0.12476114 5.147452 ]
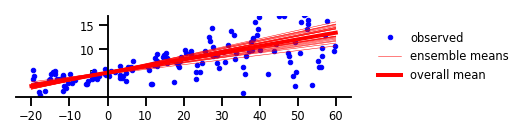
Figure 3: Epistemic Uncertainty
plt.figure(figsize=[6, 1.5]) # inches
plt.clf();
plt.plot(x, y, 'b.', label='observed');
yhats = [model(x_tst) for _ in range(100)]
avgm = np.zeros_like(x_tst[..., 0])
for i, yhat in enumerate(yhats):
m = np.squeeze(yhat.mean())
s = np.squeeze(yhat.stddev())
if i < 25:
plt.plot(x_tst, m, 'r', label='ensemble means' if i == 0 else None, linewidth=0.5)
avgm += m
plt.plot(x_tst, avgm/len(yhats), 'r', label='overall mean', linewidth=4)
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig3.png', bbox_inches='tight', dpi=300)
Case 4: Aleatoric & Epistemic Uncertainty
# Build model.
model = tf_keras.Sequential([
tfp.layers.DenseVariational(1 + 1, posterior_mean_field, prior_trainable, kl_weight=1/x.shape[0]),
tfp.layers.DistributionLambda(
lambda t: tfd.Normal(loc=t[..., :1],
scale=1e-3 + tf.math.softplus(0.01 * t[...,1:]))),
])
# Do inference.
model.compile(optimizer=tf_keras.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
[ 0.12753433 2.7504077 5.160624 3.8251898 -3.4283297 -0.8961645 -2.2378397 0.1496858 ] [0.14511648 2.7104297 5.1248145 3.7724588 ]
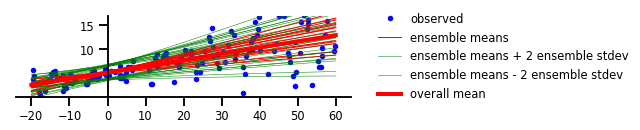
Figure 4: Both Aleatoric & Epistemic Uncertainty
plt.figure(figsize=[6, 1.5]) # inches
plt.plot(x, y, 'b.', label='observed');
yhats = [model(x_tst) for _ in range(100)]
avgm = np.zeros_like(x_tst[..., 0])
for i, yhat in enumerate(yhats):
m = np.squeeze(yhat.mean())
s = np.squeeze(yhat.stddev())
if i < 15:
plt.plot(x_tst, m, 'r', label='ensemble means' if i == 0 else None, linewidth=1.)
plt.plot(x_tst, m + 2 * s, 'g', linewidth=0.5, label='ensemble means + 2 ensemble stdev' if i == 0 else None);
plt.plot(x_tst, m - 2 * s, 'g', linewidth=0.5, label='ensemble means - 2 ensemble stdev' if i == 0 else None);
avgm += m
plt.plot(x_tst, avgm/len(yhats), 'r', label='overall mean', linewidth=4)
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig4.png', bbox_inches='tight', dpi=300)
Case 5: Functional Uncertainty
Custom PSD Kernel
class RBFKernelFn(tf_keras.layers.Layer):
def __init__(self, **kwargs):
super(RBFKernelFn, self).__init__(**kwargs)
dtype = kwargs.get('dtype', None)
self._amplitude = self.add_variable(
initializer=tf.constant_initializer(0),
dtype=dtype,
name='amplitude')
self._length_scale = self.add_variable(
initializer=tf.constant_initializer(0),
dtype=dtype,
name='length_scale')
def call(self, x):
# Never called -- this is just a layer so it can hold variables
# in a way Keras understands.
return x
@property
def kernel(self):
return tfp.math.psd_kernels.ExponentiatedQuadratic(
amplitude=tf.nn.softplus(0.1 * self._amplitude),
length_scale=tf.nn.softplus(5. * self._length_scale)
)
# For numeric stability, set the default floating-point dtype to float64
tf_keras.backend.set_floatx('float64')
# Build model.
num_inducing_points = 40
model = tf_keras.Sequential([
tf_keras.layers.InputLayer(input_shape=[1]),
tf_keras.layers.Dense(1, kernel_initializer='ones', use_bias=False),
tfp.layers.VariationalGaussianProcess(
num_inducing_points=num_inducing_points,
kernel_provider=RBFKernelFn(),
event_shape=[1],
inducing_index_points_initializer=tf.constant_initializer(
np.linspace(*x_range, num=num_inducing_points,
dtype=x.dtype)[..., np.newaxis]),
unconstrained_observation_noise_variance_initializer=(
tf.constant_initializer(np.array(0.54).astype(x.dtype))),
),
])
# Do inference.
batch_size = 32
loss = lambda y, rv_y: rv_y.variational_loss(
y, kl_weight=np.array(batch_size, x.dtype) / x.shape[0])
model.compile(optimizer=tf_keras.optimizers.Adam(learning_rate=0.01), loss=loss)
model.fit(x, y, batch_size=batch_size, epochs=1000, verbose=False)
# Profit.
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
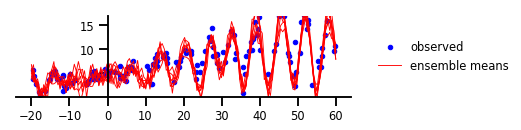
Figure 5: Functional Uncertainty
y, x, _ = load_dataset()
plt.figure(figsize=[6, 1.5]) # inches
plt.plot(x, y, 'b.', label='observed');
num_samples = 7
for i in range(num_samples):
sample_ = yhat.sample().numpy()
plt.plot(x_tst,
sample_[..., 0].T,
'r',
linewidth=0.9,
label='ensemble means' if i == 0 else None);
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig5.png', bbox_inches='tight', dpi=300)