此笔记本说明了将结构时间序列模型拟合到时间序列并使用它们生成预测和解释的两个示例。
 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 运行 在 Google Colab 运行
|
 在 Github 上查看源代码 在 Github 上查看源代码
|
 下载笔记本 下载笔记本
|
依赖项和前提条件
Import and set ups
%matplotlib inline
import matplotlib as mpl
from matplotlib import pylab as plt
import matplotlib.dates as mdates
import seaborn as sns
import collections
import numpy as np
import jax
from jax.config import config
config.update('jax_enable_x64', True)
from tensorflow_probability.substrates import jax as tfp
import jax.numpy as jnp
import optax
tfd = tfp.distributions
sts = tfp.sts
加快速度!
在深入探究之前,请确保我们在此演示中使用 GPU。
为此,请选择“Runtime -> Change runtime type -> Hardware accelerator -> GPU”。
以下代码段将验证我们是否可以使用 GPU。
if jax.default_backend() != 'gpu':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU.')
SUCCESS: Found GPU.
注:如果由于某种原因无法使用 GPU,则此 Colab 仍然有效。(训练将花费更长时间。)
绘制设置
绘制时间序列和预测的 Helper 方法。
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
sns.set_context("notebook", font_scale=1.)
sns.set_style("whitegrid")
%config InlineBackend.figure_format = 'retina'
def plot_forecast(x, y,
forecast_mean, forecast_scale, forecast_samples,
title, x_locator=None, x_formatter=None):
"""Plot a forecast distribution against the 'true' time series."""
colors = sns.color_palette()
c1, c2 = colors[0], colors[1]
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(1, 1, 1)
num_steps = len(y)
num_steps_forecast = forecast_mean.shape[-1]
num_steps_train = num_steps - num_steps_forecast
ax.plot(x, y, lw=2, color=c1, label='ground truth')
forecast_steps = np.arange(
x[num_steps_train],
x[num_steps_train]+num_steps_forecast,
dtype=x.dtype)
ax.plot(forecast_steps, forecast_samples.T, lw=1, color=c2, alpha=0.1)
ax.plot(forecast_steps, forecast_mean, lw=2, ls='--', color=c2,
label='forecast')
ax.fill_between(forecast_steps,
forecast_mean-2*forecast_scale,
forecast_mean+2*forecast_scale, color=c2, alpha=0.2)
ymin, ymax = min(jnp.min(forecast_samples), jnp.min(y)), max(jnp.max(forecast_samples), jnp.max(y))
yrange = ymax-ymin
ax.set_ylim([ymin - yrange*0.1, ymax + yrange*0.1])
ax.set_title("{}".format(title))
ax.legend()
if x_locator is not None:
ax.xaxis.set_major_locator(x_locator)
ax.xaxis.set_major_formatter(x_formatter)
fig.autofmt_xdate()
return fig, ax
def plot_components(dates,
component_means_dict,
component_stddevs_dict,
x_locator=None,
x_formatter=None):
"""Plot the contributions of posterior components in a single figure."""
colors = sns.color_palette()
c1, c2 = colors[0], colors[1]
axes_dict = collections.OrderedDict()
num_components = len(component_means_dict)
fig = plt.figure(figsize=(12, 2.5 * num_components))
for i, component_name in enumerate(component_means_dict.keys()):
component_mean = component_means_dict[component_name]
component_stddev = component_stddevs_dict[component_name]
ax = fig.add_subplot(num_components,1,1+i)
ax.plot(dates, component_mean, lw=2)
ax.fill_between(dates,
component_mean-2*component_stddev,
component_mean+2*component_stddev,
color=c2, alpha=0.5)
ax.set_title(component_name)
if x_locator is not None:
ax.xaxis.set_major_locator(x_locator)
ax.xaxis.set_major_formatter(x_formatter)
axes_dict[component_name] = ax
fig.autofmt_xdate()
fig.tight_layout()
return fig, axes_dict
def plot_one_step_predictive(dates, observed_time_series,
one_step_mean, one_step_scale,
x_locator=None, x_formatter=None):
"""Plot a time series against a model's one-step predictions."""
colors = sns.color_palette()
c1, c2 = colors[0], colors[1]
fig=plt.figure(figsize=(12, 6))
ax = fig.add_subplot(1,1,1)
num_timesteps = one_step_mean.shape[-1]
ax.plot(dates, observed_time_series, label="observed time series", color=c1)
ax.plot(dates, one_step_mean, label="one-step prediction", color=c2)
ax.fill_between(dates,
one_step_mean - one_step_scale,
one_step_mean + one_step_scale,
alpha=0.1, color=c2)
ax.legend()
if x_locator is not None:
ax.xaxis.set_major_locator(x_locator)
ax.xaxis.set_major_formatter(x_formatter)
fig.autofmt_xdate()
fig.tight_layout()
return fig, ax
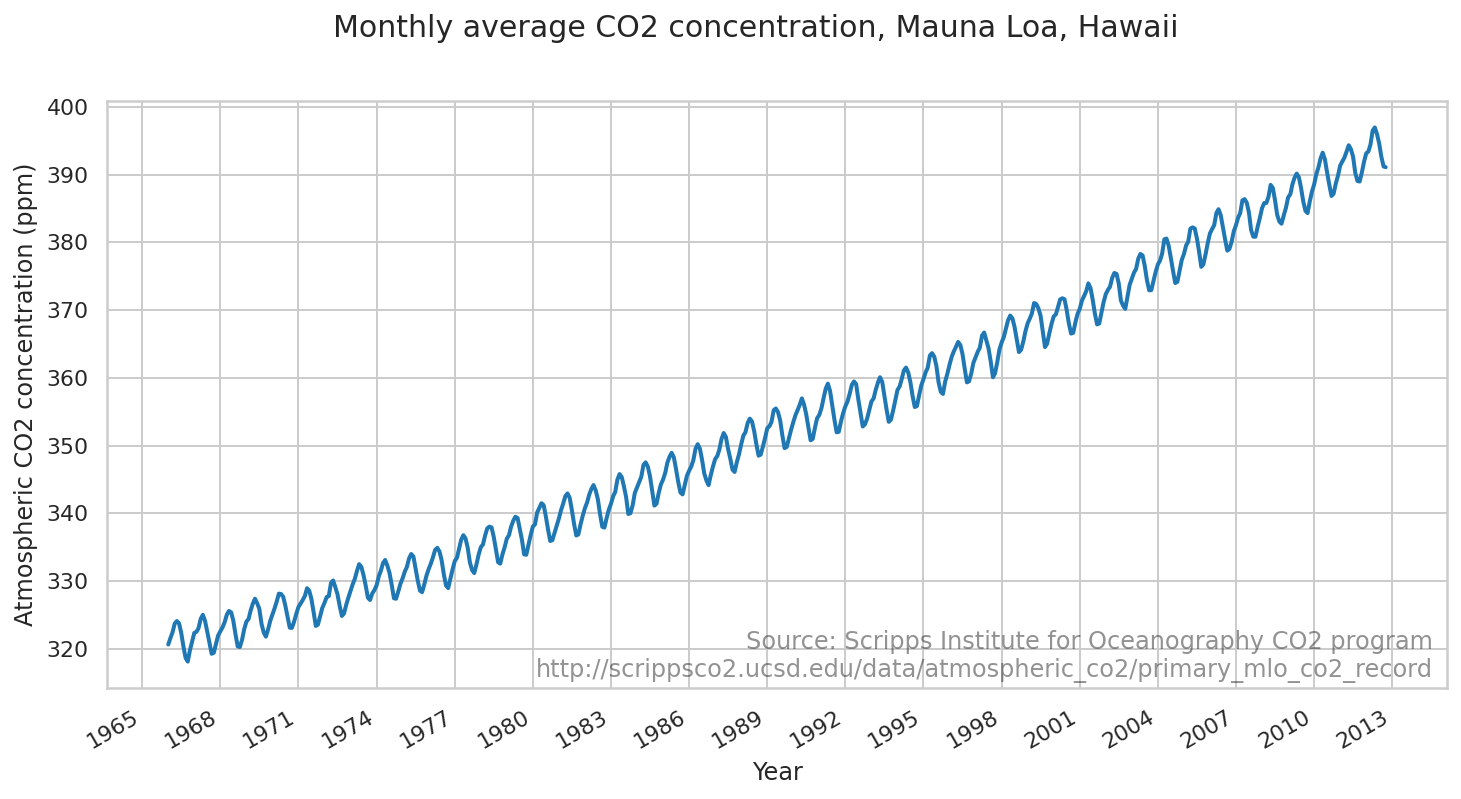
茂纳罗亚火山 CO2 记录
我们会演示如何将模型拟合到来自茂纳罗亚火山天文台的大气 CO2 读数。
数据
# CO2 readings from Mauna Loa observatory, monthly beginning January 1966
# Original source: http://scrippsco2.ucsd.edu/data/atmospheric_co2/primary_mlo_co2_record
co2_by_month = np.array('320.62,321.6,322.39,323.7,324.08,323.75,322.37,320.36,318.64,318.1,319.78,321.02,322.33,322.5,323.03,324.41,325,324.09,322.54,320.92,319.25,319.39,320.72,321.95,322.57,323.15,323.89,325.02,325.57,325.36,324.14,322.11,320.33,320.25,321.32,322.89,324,324.41,325.63,326.66,327.38,326.71,325.88,323.66,322.38,321.78,322.85,324.11,325.06,325.99,326.93,328.13,328.08,327.67,326.34,324.68,323.1,323.07,324.01,325.13,326.17,326.68,327.18,327.78,328.93,328.57,327.36,325.43,323.36,323.56,324.8,326.01,326.77,327.63,327.75,329.72,330.07,329.09,328.04,326.32,324.84,325.2,326.5,327.55,328.55,329.56,330.3,331.5,332.48,332.07,330.87,329.31,327.52,327.19,328.16,328.65,329.36,330.71,331.49,332.65,333.1,332.26,331.18,329.4,327.44,327.38,328.46,329.58,330.41,331.41,332.05,333.32,333.98,333.62,331.91,330.06,328.57,328.35,329.5,330.77,331.76,332.58,333.5,334.59,334.89,334.34,333.06,330.95,329.31,328.95,330.32,331.69,332.94,333.43,334.71,336.08,336.76,336.28,334.93,332.76,331.6,331.17,332.41,333.86,334.98,335.4,336.65,337.76,338.02,337.91,336.55,334.69,332.77,332.56,333.93,334.96,336.24,336.77,337.97,338.89,339.48,339.3,337.74,336.1,333.93,333.87,335.3,336.74,338.03,338.37,340.09,340.78,341.48,341.19,339.57,337.61,335.9,336.03,337.12,338.23,339.25,340.5,341.4,342.52,342.93,342.27,340.5,338.45,336.71,336.88,338.38,339.63,340.77,341.63,342.72,343.59,344.16,343.37,342.07,339.83,338,337.88,339.28,340.51,341.4,342.54,343.12,344.96,345.78,345.34,344,342.4,339.89,340.01,341.16,342.98,343.82,344.62,345.38,347.15,347.52,346.88,345.47,343.34,341.13,341.4,343.02,344.25,344.99,346.01,347.43,348.34,348.92,348.24,346.54,344.64,343.06,342.78,344.21,345.53,346.28,346.93,347.83,349.53,350.19,349.54,347.92,345.88,344.83,344.15,345.64,346.88,348,348.47,349.41,350.97,351.84,351.25,349.5,348.08,346.44,346.1,347.54,348.69,350.16,351.47,351.96,353.33,353.97,353.55,352.14,350.19,348.5,348.66,349.85,351.12,352.55,352.86,353.48,355.21,355.47,354.92,353.7,351.47,349.61,349.79,351.09,352.32,353.46,354.5,355.19,356,356.96,356.04,354.62,352.71,350.77,350.99,352.64,354.02,354.53,355.55,356.96,358.4,359.14,358.04,355.98,353.81,351.95,352.02,353.55,354.79,355.79,356.52,357.61,358.95,359.46,359.05,356.82,354.8,352.81,353.11,353.96,355.2,356.5,356.97,358.18,359.26,360.08,359.4,357.38,355.33,353.5,353.8,355.15,356.62,358.19,358.73,359.79,361.09,361.51,360.78,359.38,357.31,355.68,355.83,357.42,358.87,359.81,360.84,361.48,363.3,363.64,363.11,361.75,359.31,357.91,357.62,359.42,360.56,361.91,363.11,363.89,364.58,365.29,364.84,363.52,361.35,359.32,359.48,360.64,362.21,363.06,363.87,364.44,366.23,366.68,365.52,364.36,362.39,360.08,360.67,362.32,364.17,365.22,366.04,367.2,368.5,369.19,368.77,367.53,365.67,363.8,364.13,365.36,366.87,368.05,368.77,369.49,371.04,370.9,370.25,369.17,366.83,364.54,365.04,366.58,367.92,369.05,369.37,370.42,371.57,371.74,371.6,370.02,368.03,366.53,366.64,368.2,369.44,370.2,371.42,372.04,372.78,373.94,373.23,371.54,369.47,367.88,368.02,369.6,371.16,372.36,373,373.44,374.77,375.48,375.33,373.95,371.41,370.63,370.18,372.01,373.71,374.61,375.55,376.04,377.58,378.28,378.07,376.54,374.42,372.92,372.94,374.29,375.63,376.73,377.31,378.33,380.44,380.56,379.49,377.71,375.77,373.99,374.17,375.79,377.39,378.29,379.56,380.07,382.01,382.21,382.05,380.63,378.64,376.38,376.77,378.27,379.92,381.33,381.98,382.53,384.33,384.89,384,382.25,380.44,378.77,379.03,380.11,381.63,382.55,383.68,384.31,386.2,386.38,385.85,384.42,381.81,380.83,380.83,382.32,383.58,385.04,385.81,385.8,386.74,388.48,388.02,386.22,384.05,383.05,382.75,383.98,385.08,386.63,387.1,388.5,389.54,390.15,389.6,388.05,386.06,384.64,384.32,386.05,387.48,388.55,390.08,391.02,392.39,393.24,392.26,390.35,388.53,386.85,387.18,388.69,389.83,391.33,391.96,392.49,393.4,394.33,393.75,392.64,390.25,389.05,388.98,390.3,391.86,393.13,393.42,394.43,396.51,396.96,395.97,394.6,392.61,391.2,391.09,393.03,394.42,395.69,396.94,397.35,398.44,400.06,398.96,397.45,395.49,393.47,393.77,395.27,396.9,398.01,398.18,399.56,401.44,401.98,401.41,399.17,397.3,395.49,395.74,397.32,398.88,399.94,400.4,401.6,403.52,404.03,402.81,401.54,398.93,397.43,398.22,400.17,401.82,402.58,404.09,404.79,407.5,407.59,406.94,404.43,402.17,400.95,401.43,403.57,404.48,406,406.57,406.99,408.88,409.84,409.05,407.13,405.17,403.2,403.57,405.1,406.68,407.98,408.36,409.21,410.24,411.23,410.81,408.83,407.02,405.53,405.93,408.04,409.17,410.85,411.59,411.91,413.46,414.76,413.89,411.78,410.01,408.48,408.4,410.16,411.81,413.3,414.05,414.45,416.11,417.15,416.29,414.42,412.52,411.18,411.12,412.88,413.89,415.15,416.47,417.16,418.24,418.95,418.7,416.65,414.34,412.91,413.55,414.82,416.43,418.01,418.99,418.45,420.02,420.77,420.68,418.68,416.76,415.41,415.31'.split(',')).astype(np.float32)
co2_by_month = co2_by_month
num_forecast_steps = 12 * 10 # Forecast the final ten years, given previous data
co2_by_month_training_data = co2_by_month[:-num_forecast_steps]
co2_dates = np.arange("1966-01", "2022-11", dtype="datetime64[M]")
co2_loc = mdates.YearLocator(3)
co2_fmt = mdates.DateFormatter('%Y')
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(1, 1, 1)
ax.plot(co2_dates[:-num_forecast_steps], co2_by_month_training_data, lw=2, label="training data")
ax.xaxis.set_major_locator(co2_loc)
ax.xaxis.set_major_formatter(co2_fmt)
ax.set_ylabel("Atmospheric CO2 concentration (ppm)")
ax.set_xlabel("Year")
fig.suptitle("Monthly average CO2 concentration, Mauna Loa, Hawaii",
fontsize=15)
ax.text(0.99, .02,
"Source: Scripps Institute for Oceanography CO2 program\nhttp://scrippsco2.ucsd.edu/data/atmospheric_co2/primary_mlo_co2_record",
transform=ax.transAxes,
horizontalalignment="right",
alpha=0.5)
fig.autofmt_xdate()
模型与拟合
我们将使用局部线性趋势以及一年中某个月的季节性效应对此序列进行建模。
def build_model(observed_time_series):
trend = sts.LocalLinearTrend(observed_time_series=observed_time_series)
seasonal = tfp.sts.Seasonal(
num_seasons=12, observed_time_series=observed_time_series)
model = sts.Sum([trend, seasonal], observed_time_series=observed_time_series)
return model
我们将使用变分推断来拟合模型。这涉及运行优化器以最小化变分损失函数,即负证据下限 (ELBO)。这会拟合参数的一组近似后验分布(实际上,我们假设它们是转换为每个参数的支持空间的独立法线)。
tfp.sts 预测方法需要后验样本作为输入,因此我们将通过从变分后验中抽取一组样本来结束。
co2_model = build_model(co2_by_month_training_data)
# Build the variational surrogate posteriors `qs`.
init_fn, build_surrogate_fn = (
tfp.sts.build_factored_surrogate_posterior_stateless(model=co2_model))
Minimize the variational loss.
# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 200 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)
seed = jax.random.PRNGKey(42)
init_seed, fit_seed, sample_seed = jax.random.split(seed, 3)
initial_parameters = init_fn(init_seed)
jd = co2_model.joint_distribution(co2_by_month_training_data)
# Build and optimize the variational loss function.
optimized_parameters, elbo_loss_curve = tfp.vi.fit_surrogate_posterior_stateless(
target_log_prob_fn=jd.log_prob,
initial_parameters=initial_parameters,
build_surrogate_posterior_fn=build_surrogate_fn,
optimizer=optax.adam(0.1),
num_steps=num_variational_steps,
seed=fit_seed)
plt.plot(elbo_loss_curve)
plt.show()
# Draw samples from the variational posterior.
variational_posteriors = build_surrogate_fn(optimized_parameters)
q_samples_co2_ = variational_posteriors.sample(50, seed=sample_seed)
print("Inferred parameters:")
for param in co2_model.parameters:
print("{}: {} +- {}".format(param.name,
jnp.mean(q_samples_co2_[param.name], axis=0),
jnp.std(q_samples_co2_[param.name], axis=0)))
Inferred parameters: observation_noise_scale: 0.1685197800397873 +- 0.007219966035336256 LocalLinearTrend_level_scale: 0.18049846589565277 +- 0.011273686774075031 LocalLinearTrend_slope_scale: 0.009398984722793102 +- 0.0021420123521238565 Seasonal_drift_scale: 0.03475992754101753 +- 0.005793483462184668
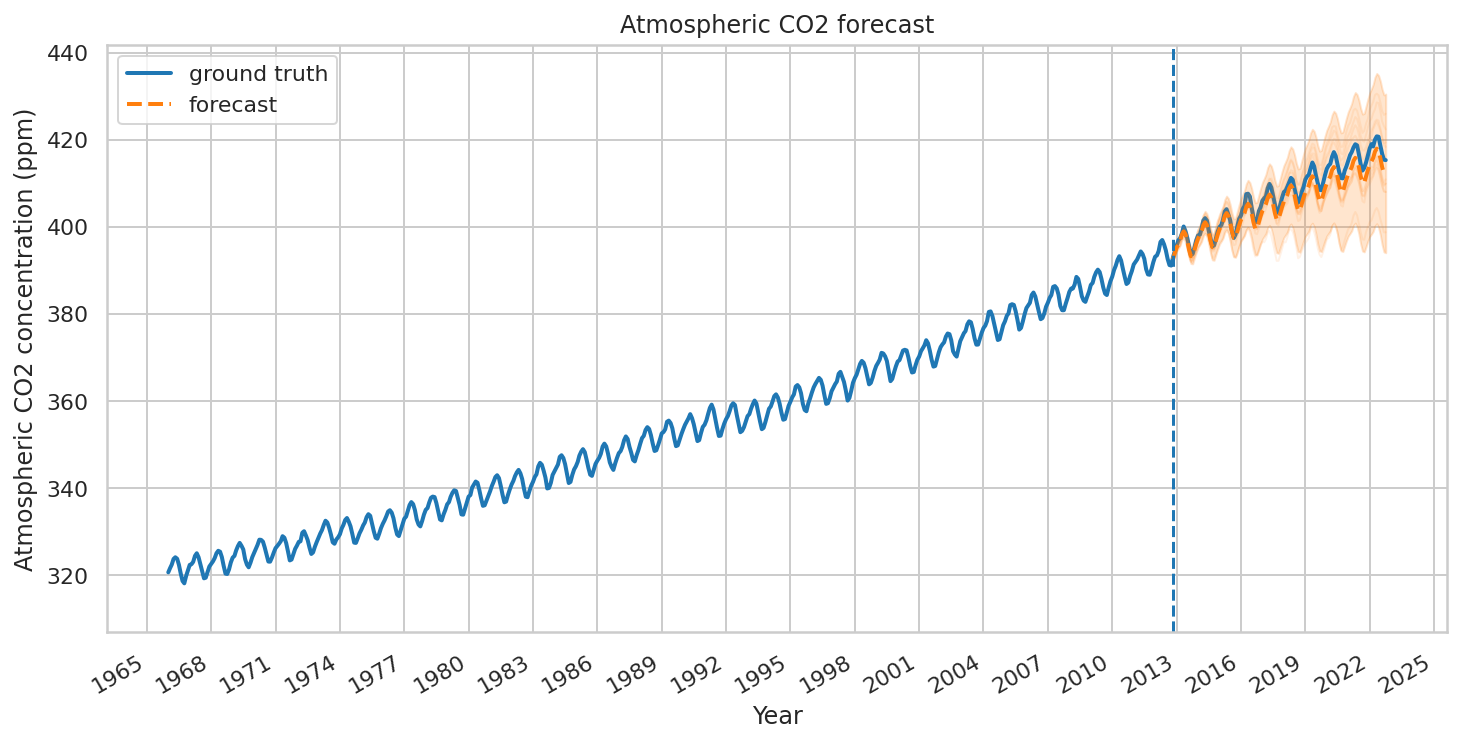
预测与驳斥
现在,我们使用拟合模型来构造预测。我们只调用 tfp.sts.forecast,它会返回一个 TensorFlow Distribution 实例,表示在未来时间步骤的预测分布。
co2_forecast_dist = tfp.sts.forecast(
co2_model,
observed_time_series=co2_by_month_training_data,
parameter_samples=q_samples_co2_,
num_steps_forecast=num_forecast_steps)
特别是,预测分布的 mean 和 stddev 会为我们提供在每个时间步骤具有边际不确定性的预测,而且我们还可以绘制可能的未来的样本。
num_samples=10
co2_forecast_mean, co2_forecast_scale, co2_forecast_samples = (
co2_forecast_dist.mean()[..., 0],
co2_forecast_dist.stddev()[..., 0],
co2_forecast_dist.sample(num_samples, seed=sample_seed)[..., 0])
fig, ax = plot_forecast(
co2_dates, co2_by_month,
co2_forecast_mean, co2_forecast_scale, co2_forecast_samples,
x_locator=co2_loc,
x_formatter=co2_fmt,
title="Atmospheric CO2 forecast")
ax.axvline(co2_dates[-num_forecast_steps], linestyle="--")
ax.legend(loc="upper left")
ax.set_ylabel("Atmospheric CO2 concentration (ppm)")
ax.set_xlabel("Year")
fig.autofmt_xdate()
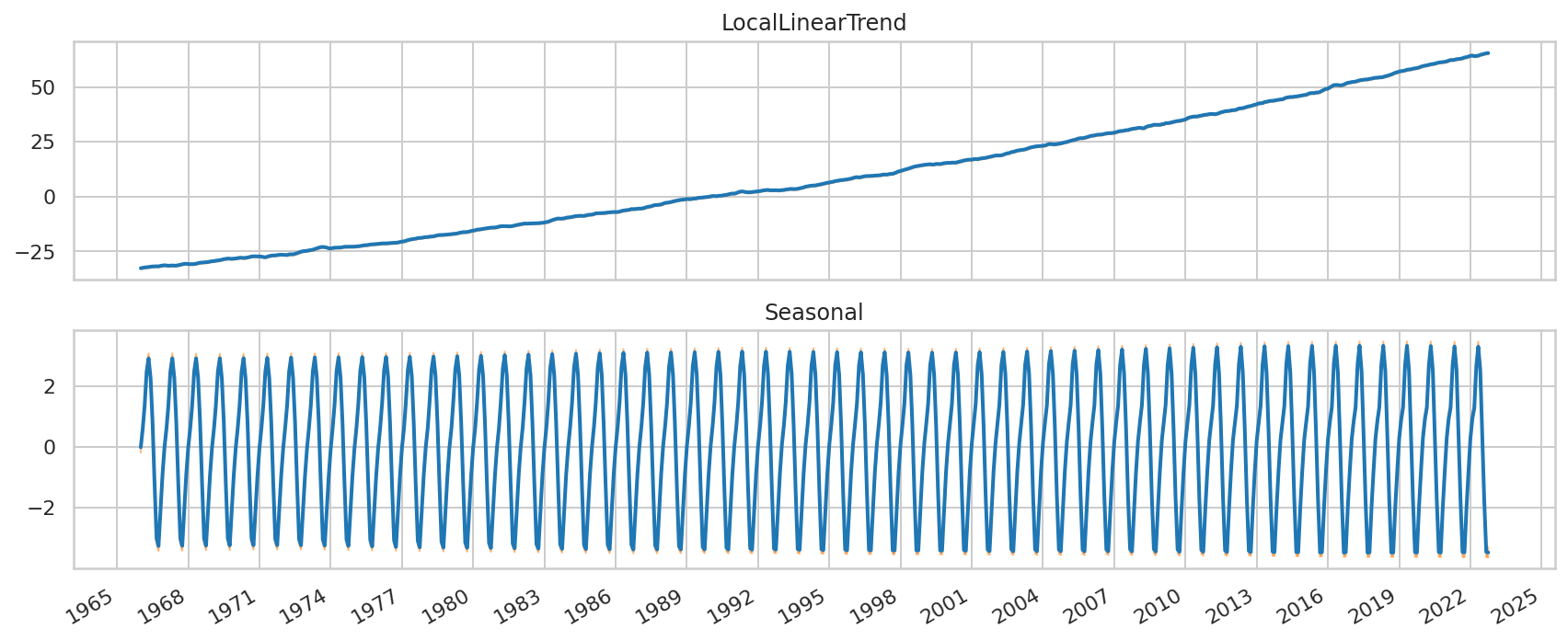
我们可以通过将模型分解为个别时间序列的贡献来进一步理解模型的拟合:
# Build a dict mapping components to distributions over
# their contribution to the observed signal.
component_dists = sts.decompose_by_component(
co2_model,
observed_time_series=co2_by_month,
parameter_samples=q_samples_co2_)
co2_component_means_, co2_component_stddevs_ = (
{k.name: c.mean() for k, c in component_dists.items()},
{k.name: c.stddev() for k, c in component_dists.items()})
_ = plot_components(co2_dates, co2_component_means_, co2_component_stddevs_,
x_locator=co2_loc, x_formatter=co2_fmt)
电力需求预测
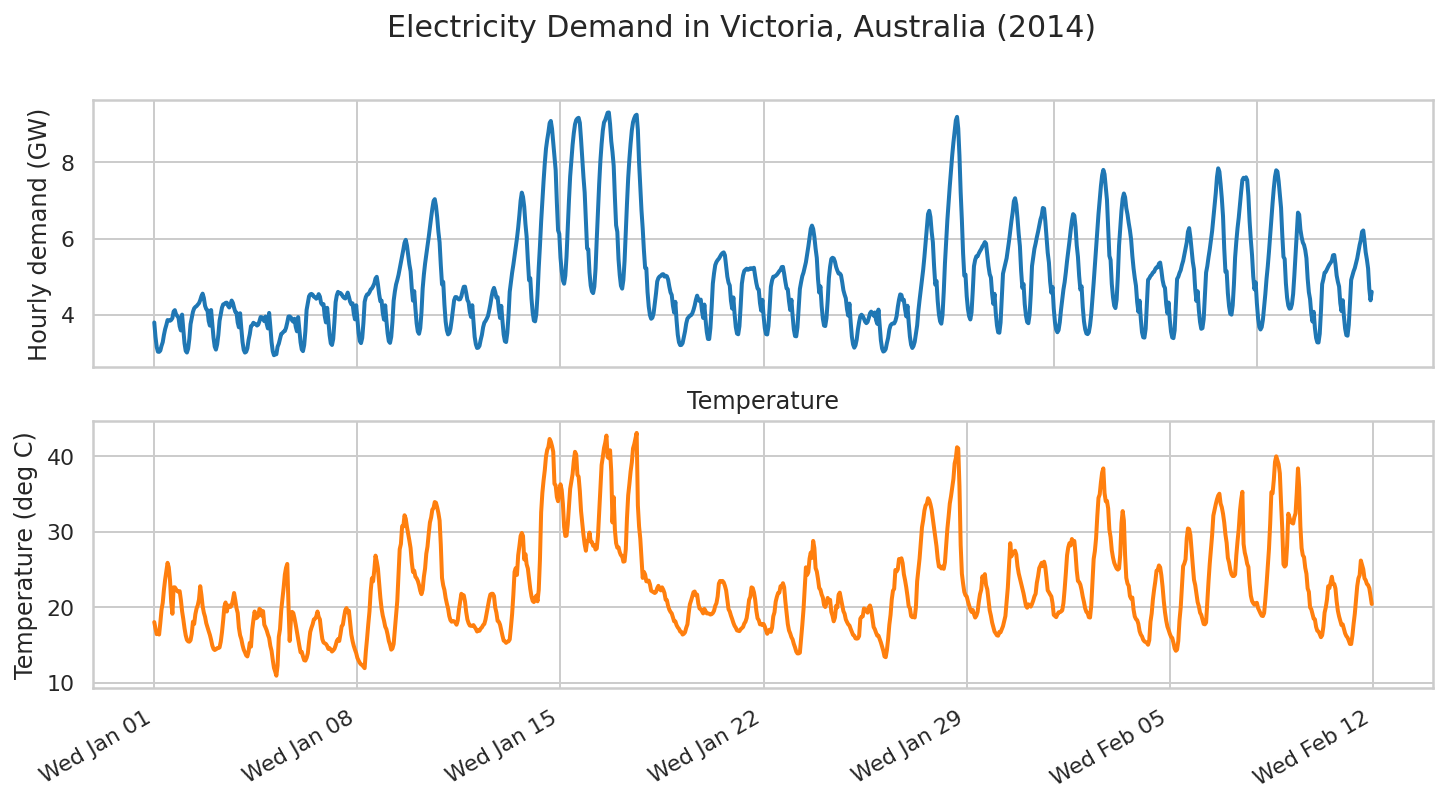
现在,我们考虑一个更复杂的示例:预测澳大利亚维多利亚州的电力需求。
首先,我们将构建数据集:
# Victoria electricity demand dataset, as presented at
# https://otexts.com/fpp2/scatterplots.html
# and downloaded from https://github.com/robjhyndman/fpp2-package/blob/master/data/elecdaily.rda
# This series contains the first eight weeks (starting Jan 1). The original
# dataset was half-hourly data; here we've downsampled to hourly data by taking
# every other timestep.
demand_dates = np.arange('2014-01-01', '2014-02-26', dtype='datetime64[h]')
demand_loc = mdates.WeekdayLocator(byweekday=mdates.WE)
demand_fmt = mdates.DateFormatter('%a %b %d')
demand = np.array("3.794,3.418,3.152,3.026,3.022,3.055,3.180,3.276,3.467,3.620,3.730,3.858,3.851,3.839,3.861,3.912,4.082,4.118,4.011,3.965,3.932,3.693,3.585,4.001,3.623,3.249,3.047,3.004,3.104,3.361,3.749,3.910,4.075,4.165,4.202,4.225,4.265,4.301,4.381,4.484,4.552,4.440,4.233,4.145,4.116,3.831,3.712,4.121,3.764,3.394,3.159,3.081,3.216,3.468,3.838,4.012,4.183,4.269,4.280,4.310,4.315,4.233,4.188,4.263,4.370,4.308,4.182,4.075,4.057,3.791,3.667,4.036,3.636,3.283,3.073,3.003,3.023,3.113,3.335,3.484,3.697,3.723,3.786,3.763,3.748,3.714,3.737,3.828,3.937,3.929,3.877,3.829,3.950,3.756,3.638,4.045,3.682,3.283,3.036,2.933,2.956,2.959,3.157,3.236,3.370,3.493,3.516,3.555,3.570,3.656,3.792,3.950,3.953,3.926,3.849,3.813,3.891,3.683,3.562,3.936,3.602,3.271,3.085,3.041,3.201,3.570,4.123,4.307,4.481,4.533,4.545,4.524,4.470,4.457,4.418,4.453,4.539,4.473,4.301,4.260,4.276,3.958,3.796,4.180,3.843,3.465,3.246,3.203,3.360,3.808,4.328,4.509,4.598,4.562,4.566,4.532,4.477,4.442,4.424,4.486,4.579,4.466,4.338,4.270,4.296,4.034,3.877,4.246,3.883,3.520,3.306,3.252,3.387,3.784,4.335,4.465,4.529,4.536,4.589,4.660,4.691,4.747,4.819,4.950,4.994,4.798,4.540,4.352,4.370,4.047,3.870,4.245,3.848,3.509,3.302,3.258,3.419,3.809,4.363,4.605,4.793,4.908,5.040,5.204,5.358,5.538,5.708,5.888,5.966,5.817,5.571,5.321,5.141,4.686,4.367,4.618,4.158,3.771,3.555,3.497,3.646,4.053,4.687,5.052,5.342,5.586,5.808,6.038,6.296,6.548,6.787,6.982,7.035,6.855,6.561,6.181,5.899,5.304,4.795,4.862,4.264,3.820,3.588,3.481,3.514,3.632,3.857,4.116,4.375,4.462,4.460,4.422,4.398,4.407,4.480,4.621,4.732,4.735,4.572,4.385,4.323,4.069,3.940,4.247,3.821,3.416,3.220,3.124,3.132,3.181,3.337,3.469,3.668,3.788,3.834,3.894,3.964,4.109,4.275,4.472,4.623,4.703,4.594,4.447,4.459,4.137,3.913,4.231,3.833,3.475,3.302,3.279,3.519,3.975,4.600,4.864,5.104,5.308,5.542,5.759,6.005,6.285,6.617,6.993,7.207,7.095,6.839,6.387,6.048,5.433,4.904,4.959,4.425,4.053,3.843,3.823,4.017,4.521,5.229,5.802,6.449,6.975,7.506,7.973,8.359,8.596,8.794,9.030,9.090,8.885,8.525,8.147,7.797,6.938,6.215,6.123,5.495,5.140,4.896,4.812,5.024,5.536,6.293,7.000,7.633,8.030,8.459,8.768,9.000,9.113,9.155,9.173,9.039,8.606,8.095,7.617,7.208,6.448,5.740,5.718,5.106,4.763,4.610,4.566,4.737,5.204,5.988,6.698,7.438,8.040,8.484,8.837,9.052,9.114,9.214,9.307,9.313,9.006,8.556,8.275,7.911,7.077,6.348,6.175,5.455,5.041,4.759,4.683,4.908,5.411,6.199,6.923,7.593,8.090,8.497,8.843,9.058,9.159,9.231,9.253,8.852,7.994,7.388,6.735,6.264,5.690,5.227,5.220,4.593,4.213,3.984,3.891,3.919,4.031,4.287,4.558,4.872,4.963,5.004,5.017,5.057,5.064,5.000,5.023,5.007,4.923,4.740,4.586,4.517,4.236,4.055,4.337,3.848,3.473,3.273,3.198,3.204,3.252,3.404,3.560,3.767,3.896,3.934,3.972,3.985,4.032,4.122,4.239,4.389,4.499,4.406,4.356,4.396,4.106,3.914,4.265,3.862,3.546,3.360,3.359,3.649,4.180,4.813,5.086,5.301,5.384,5.434,5.470,5.529,5.582,5.618,5.636,5.561,5.291,5.000,4.840,4.767,4.364,4.160,4.452,4.011,3.673,3.503,3.483,3.695,4.213,4.810,5.028,5.149,5.182,5.208,5.179,5.190,5.220,5.202,5.216,5.232,5.019,4.828,4.686,4.657,4.304,4.106,4.389,3.955,3.643,3.489,3.479,3.695,4.187,4.732,4.898,4.997,5.001,5.022,5.052,5.094,5.143,5.178,5.250,5.255,5.075,4.867,4.691,4.665,4.352,4.121,4.391,3.966,3.615,3.437,3.430,3.666,4.149,4.674,4.851,5.011,5.105,5.242,5.378,5.576,5.790,6.030,6.254,6.340,6.253,6.039,5.736,5.490,4.936,4.580,4.742,4.230,3.895,3.712,3.700,3.906,4.364,4.962,5.261,5.463,5.495,5.477,5.394,5.250,5.159,5.081,5.083,5.038,4.857,4.643,4.526,4.428,4.141,3.975,4.290,3.809,3.423,3.217,3.132,3.192,3.343,3.606,3.803,3.963,3.998,3.962,3.894,3.814,3.776,3.808,3.914,4.033,4.079,4.027,3.974,4.057,3.859,3.759,4.132,3.716,3.325,3.111,3.030,3.046,3.096,3.254,3.390,3.606,3.718,3.755,3.768,3.768,3.834,3.957,4.199,4.393,4.532,4.516,4.380,4.390,4.142,3.954,4.233,3.795,3.425,3.209,3.124,3.177,3.288,3.498,3.715,4.092,4.383,4.644,4.909,5.184,5.518,5.889,6.288,6.643,6.729,6.567,6.179,5.903,5.278,4.788,4.885,4.363,4.011,3.823,3.762,3.998,4.598,5.349,5.898,6.487,6.941,7.381,7.796,8.185,8.522,8.825,9.103,9.198,8.889,8.174,7.214,6.481,5.611,5.026,5.052,4.484,4.148,3.955,3.873,4.060,4.626,5.272,5.441,5.535,5.534,5.610,5.671,5.724,5.793,5.838,5.908,5.868,5.574,5.276,5.065,4.976,4.554,4.282,4.547,4.053,3.720,3.536,3.524,3.792,4.420,5.075,5.208,5.344,5.482,5.701,5.936,6.210,6.462,6.683,6.979,7.059,6.893,6.535,6.121,5.797,5.152,4.705,4.805,4.272,3.975,3.805,3.775,3.996,4.535,5.275,5.509,5.730,5.870,6.034,6.175,6.340,6.500,6.603,6.804,6.787,6.460,6.043,5.627,5.367,4.866,4.575,4.728,4.157,3.795,3.607,3.537,3.596,3.803,4.125,4.398,4.660,4.853,5.115,5.412,5.669,5.930,6.216,6.466,6.641,6.605,6.316,5.821,5.520,5.016,4.657,4.746,4.197,3.823,3.613,3.505,3.488,3.532,3.716,4.011,4.421,4.836,5.296,5.766,6.233,6.646,7.011,7.380,7.660,7.804,7.691,7.364,7.019,6.260,5.545,5.437,4.806,4.457,4.235,4.172,4.396,5.002,5.817,6.266,6.732,7.049,7.184,7.085,6.798,6.632,6.408,6.218,5.968,5.544,5.217,4.964,4.758,4.328,4.074,4.367,3.883,3.536,3.404,3.396,3.624,4.271,4.916,4.953,5.016,5.048,5.106,5.124,5.200,5.244,5.242,5.341,5.368,5.166,4.910,4.762,4.700,4.276,4.035,4.318,3.858,3.550,3.399,3.382,3.590,4.261,4.937,4.994,5.094,5.168,5.303,5.410,5.571,5.740,5.900,6.177,6.274,6.039,5.700,5.389,5.192,4.672,4.359,4.614,4.118,3.805,3.627,3.646,3.882,4.470,5.106,5.274,5.507,5.711,5.950,6.200,6.527,6.884,7.196,7.615,7.845,7.759,7.437,7.059,6.584,5.742,5.125,5.139,4.564,4.218,4.025,4.000,4.245,4.783,5.504,5.920,6.271,6.549,6.894,7.231,7.535,7.597,7.562,7.609,7.534,7.118,6.448,5.963,5.565,5.005,4.666,4.850,4.302,3.905,3.678,3.610,3.672,3.869,4.204,4.541,4.944,5.265,5.651,6.090,6.547,6.935,7.318,7.625,7.793,7.760,7.510,7.145,6.805,6.103,5.520,5.462,4.824,4.444,4.237,4.157,4.164,4.275,4.545,5.033,5.594,6.176,6.681,6.628,6.238,6.039,5.897,5.832,5.701,5.483,4.949,4.589,4.407,4.027,3.820,4.075,3.650,3.388,3.271,3.268,3.498,4.086,4.800,4.933,5.102,5.126,5.194,5.260,5.319,5.364,5.419,5.559,5.568,5.332,5.027,4.864,4.738,4.303,4.093,4.379,3.952,3.632,3.461,3.446,3.732,4.294,4.911,5.021,5.138,5.223,5.348,5.479,5.661,5.832,5.966,6.178,6.212,5.949,5.640,5.449,5.213,4.678,4.376,4.601,4.147,3.815,3.610,3.605,3.879,4.468,5.090,5.226,5.406,5.561,5.740,5.899,6.095,6.272,6.402,6.610,6.585,6.265,5.925,5.747,5.497,4.932,4.580,4.763,4.298,4.026,3.871,3.827,4.065,4.643,5.317,5.494,5.685,5.814,5.912,5.999,6.097,6.176,6.136,6.131,6.049,5.796,5.532,5.475,5.254,4.742,4.453,4.660,4.176,3.895,3.726,3.717,3.910,4.479,5.135,5.306,5.520,5.672,5.737,5.785,5.829,5.893,5.892,5.921,5.817,5.557,5.304,5.234,5.074,4.656,4.396,4.599,4.064,3.749,3.560,3.475,3.552,3.783,4.045,4.258,4.539,4.762,4.938,5.049,5.037,5.066,5.151,5.197,5.201,5.132,4.908,4.725,4.568,4.222,3.939,4.215,3.741,3.380,3.174,3.076,3.071,3.172,3.328,3.427,3.603,3.738,3.765,3.777,3.705,3.690,3.742,3.859,4.032,4.113,4.032,4.066,4.011,3.712,3.530,3.905,3.556,3.283,3.136,3.146,3.400,4.009,4.717,4.827,4.909,4.973,5.036,5.079,5.160,5.228,5.241,5.343,5.350,5.184,4.941,4.797,4.615,4.160,3.904,4.213,3.810,3.528,3.369,3.381,3.609,4.178,4.861,4.918,5.006,5.102,5.239,5.385,5.528,5.724,5.845,6.048,6.097,5.838,5.507,5.267,5.003,4.462,4.184,4.431,3.969,3.660,3.480,3.470,3.693,4.313,4.955,5.083,5.251,5.268,5.293,5.285,5.308,5.349,5.322,5.328,5.151,4.975,4.741,4.678,4.458,4.056,3.868,4.226,3.799,3.428,3.253,3.228,3.452,4.040,4.726,4.709,4.721,4.741,4.846,4.864,4.868,4.836,4.799,4.890,4.946,4.800,4.646,4.693,4.546,4.117,3.897,4.259,3.893,3.505,3.341,3.334,3.623,4.240,4.925,4.986,5.028,4.987,4.984,4.975,4.912,4.833,4.686,4.710,4.718,4.577,4.454,4.532,4.407,4.064,3.883,4.221,3.792,3.445,3.261,3.221,3.295,3.521,3.804,4.038,4.200,4.226,4.198,4.182,4.078,4.018,4.002,4.066,4.158,4.154,4.084,4.104,4.001,3.773,3.700,4.078,3.702,3.349,3.143,3.052,3.070,3.181,3.327,3.440,3.616,3.678,3.694,3.710,3.706,3.764,3.852,4.009,4.202,4.323,4.249,4.275,4.162,3.848,3.706,4.060,3.703,3.401,3.251,3.239,3.455,4.041,4.743,4.815,4.916,4.931,4.966,5.063,5.218,5.381,5.458,5.550,5.566,5.376,5.104,5.022,4.793,4.335,4.108,4.410,4.008,3.666,3.497,3.464,3.698,4.333,4.998,5.094,5.272,5.459,5.648,5.853,6.062,6.258,6.236,6.226,5.957,5.455,5.066,4.968,4.742,4.304,4.105,4.410".split(",")).astype(np.float32)
temperature = np.array("18.050,17.200,16.450,16.650,16.400,17.950,19.700,20.600,22.350,23.700,24.800,25.900,25.300,23.650,20.700,19.150,22.650,22.650,22.400,22.150,22.050,22.150,21.000,19.500,18.450,17.250,16.300,15.700,15.500,15.450,15.650,16.500,18.100,17.800,19.100,19.850,20.300,21.050,22.800,21.650,20.150,19.300,18.750,17.900,17.350,16.850,16.350,15.700,14.950,14.500,14.350,14.450,14.600,14.600,14.700,15.450,16.700,18.300,20.100,20.650,19.450,20.200,20.250,20.050,20.250,20.950,21.900,21.000,19.900,19.250,17.300,16.300,15.800,15.000,14.400,14.050,13.650,13.500,14.150,15.300,14.800,17.050,18.350,19.450,18.550,18.650,18.850,19.800,19.650,18.900,19.500,17.700,17.350,16.950,16.400,15.950,14.900,14.250,13.050,12.000,11.500,10.950,12.300,16.100,17.100,19.600,21.100,22.600,24.350,25.250,25.750,20.350,15.550,18.300,19.400,19.250,18.550,17.700,16.750,15.800,14.900,14.050,14.100,13.500,13.000,12.950,13.300,13.900,15.400,16.750,17.300,17.750,18.400,18.500,18.800,19.450,18.750,18.400,16.950,15.800,15.350,15.250,15.150,14.900,14.500,14.600,14.400,14.150,14.300,14.500,14.950,15.550,15.800,15.550,16.450,17.500,17.700,18.750,19.600,19.900,19.350,19.550,17.900,16.400,15.550,14.900,14.400,13.950,13.300,12.950,12.650,12.450,12.350,12.150,11.950,14.150,15.850,17.750,19.450,22.150,23.850,23.450,24.950,26.850,26.100,25.150,23.250,21.300,19.850,18.900,18.250,17.450,17.100,16.400,15.550,15.050,14.400,14.550,15.150,17.050,18.850,20.850,24.250,27.700,28.400,30.750,30.700,32.200,31.750,30.650,29.750,28.850,27.850,25.950,24.700,24.850,24.050,23.850,23.500,22.950,22.200,21.750,22.350,24.050,25.150,27.100,28.050,29.750,31.250,31.900,32.950,33.150,33.950,33.850,33.250,32.500,31.500,28.300,23.900,22.900,22.300,21.250,20.500,19.850,18.850,18.300,18.100,18.200,18.150,18.000,17.700,18.250,19.700,20.750,21.800,21.500,21.600,20.800,19.400,18.400,17.900,17.600,17.550,17.550,17.650,17.400,17.150,16.800,17.000,16.900,17.200,17.350,17.650,17.800,18.400,19.300,20.200,21.050,21.700,21.800,21.800,21.500,20.000,19.300,18.200,18.100,17.700,16.950,16.250,15.600,15.500,15.300,15.450,15.500,15.750,17.350,19.150,21.650,24.700,25.200,24.300,26.900,28.100,29.450,29.850,29.450,26.350,27.050,25.700,25.150,23.850,22.450,21.450,20.850,20.700,21.300,21.550,20.800,22.300,26.300,32.600,35.150,36.800,38.150,39.950,40.850,41.250,42.300,41.950,41.350,40.600,36.350,36.150,34.600,34.050,35.400,36.300,35.550,33.700,30.650,29.450,29.500,31.000,33.300,35.700,36.650,37.650,39.400,40.600,40.250,37.550,37.300,35.400,32.750,31.200,29.600,28.350,27.500,28.750,28.900,29.900,28.700,28.650,28.150,28.250,27.650,27.800,29.450,32.500,35.750,38.850,39.900,41.100,41.800,42.750,39.900,39.750,40.800,37.950,31.250,34.600,30.250,28.500,27.900,27.950,27.300,26.900,26.800,26.050,26.100,27.700,31.850,34.850,36.350,38.000,39.200,41.050,41.600,42.350,43.100,33.500,30.700,29.100,26.400,23.900,24.700,24.350,23.450,23.450,23.550,23.050,22.200,22.100,22.000,21.900,22.050,22.550,22.850,22.450,22.250,22.650,22.350,21.900,21.000,20.950,20.200,19.700,19.400,19.200,18.650,18.150,18.150,17.650,17.350,17.150,16.800,16.750,16.400,16.500,16.700,17.300,17.750,19.200,20.400,20.900,21.450,22.000,22.100,21.600,21.700,20.500,19.850,19.750,19.500,19.200,19.800,19.500,19.200,19.200,19.150,19.050,19.100,19.250,19.550,20.200,20.550,21.450,23.150,23.500,23.400,23.500,23.300,22.850,22.250,20.950,19.750,19.450,18.900,18.450,17.950,17.550,17.300,16.950,16.900,16.850,17.100,17.250,17.400,17.850,18.100,18.600,19.700,21.000,21.400,22.650,22.550,22.000,21.050,19.550,18.550,18.300,17.750,17.800,17.650,17.800,17.450,16.950,16.500,16.900,17.050,16.750,17.300,18.800,19.350,20.750,21.400,21.900,21.950,22.800,22.750,23.200,22.650,20.800,19.250,17.800,16.950,16.550,16.050,15.750,15.150,14.700,14.150,13.900,13.900,14.000,15.800,17.650,19.700,22.500,25.300,24.300,24.650,26.450,27.250,26.550,28.800,27.850,25.200,24.750,23.750,22.550,22.350,21.700,21.300,20.300,20.050,20.500,21.250,20.850,21.000,19.400,18.900,18.150,18.650,20.200,20.000,21.650,21.950,21.150,20.400,19.500,19.150,18.400,18.050,17.750,17.600,17.150,16.750,16.350,16.250,15.900,15.850,15.900,16.200,18.500,18.750,18.800,19.850,19.750,19.600,19.300,20.000,20.250,19.700,18.600,17.400,17.100,16.650,16.250,16.250,15.800,15.350,14.800,14.250,13.500,13.400,14.350,15.800,17.700,19.000,21.050,22.200,22.450,24.950,24.750,25.050,26.400,26.200,26.500,25.850,24.400,23.600,22.650,21.500,20.150,19.900,18.850,18.700,18.750,18.650,20.050,23.450,24.900,26.450,28.550,30.600,31.550,32.800,33.500,33.700,34.450,34.200,33.650,32.900,31.750,30.500,29.250,28.100,26.450,25.400,25.400,25.150,25.400,25.100,25.950,28.100,30.400,32.000,33.750,34.700,35.800,37.000,39.050,39.750,41.200,41.050,36.050,28.250,24.450,23.150,22.050,21.600,21.450,20.800,20.250,19.700,19.400,19.650,19.100,18.650,18.900,19.400,20.700,21.750,22.350,24.100,23.350,24.400,22.950,22.400,20.950,19.600,18.900,18.000,17.400,16.800,16.550,16.300,16.250,16.750,16.700,17.100,17.500,18.150,18.850,20.650,22.600,25.600,28.500,26.750,27.200,27.300,27.500,27.000,25.450,24.500,23.850,23.200,22.550,21.850,21.050,20.200,19.950,20.400,20.300,20.100,20.450,20.900,21.450,21.800,23.250,24.100,25.200,25.550,25.900,25.450,26.050,25.350,23.900,22.250,22.000,21.700,21.450,20.550,19.000,18.850,18.700,19.050,19.350,19.350,19.450,19.600,20.550,22.400,24.550,26.900,27.950,28.500,28.200,29.050,28.700,28.800,27.150,24.900,23.500,23.350,23.000,22.300,21.400,20.700,19.850,19.400,19.250,18.700,18.650,20.200,23.400,26.400,27.450,29.150,32.050,34.500,34.950,36.550,37.850,38.400,35.150,34.050,34.100,33.100,30.300,29.300,27.550,26.600,25.900,25.500,25.150,25.000,25.150,27.000,31.150,32.750,31.500,26.900,23.900,23.150,22.850,21.500,21.150,21.300,19.700,18.800,18.450,18.300,17.800,16.850,16.400,16.150,15.700,15.500,15.400,15.300,15.050,15.650,18.100,19.200,21.050,22.350,23.450,24.850,24.950,25.550,25.300,24.250,22.750,20.850,19.350,18.250,17.450,17.000,16.500,16.100,15.950,15.300,14.550,14.250,14.400,15.550,18.300,20.000,22.750,25.450,25.800,26.350,29.150,30.450,30.350,29.600,27.550,25.550,23.650,22.950,21.850,20.700,20.150,19.300,19.000,18.400,17.800,17.750,18.000,20.800,23.400,25.750,27.750,29.600,32.150,32.900,33.650,34.300,34.800,35.050,33.750,33.250,32.400,31.250,29.650,28.550,26.550,25.950,25.000,24.400,24.150,24.150,24.350,26.900,28.750,30.350,32.750,34.250,35.300,28.400,27.250,26.600,25.750,25.350,23.150,21.550,20.850,20.550,20.350,20.550,20.600,19.900,19.550,19.200,18.900,18.850,19.250,21.000,23.050,25.350,27.700,31.050,35.250,35.100,36.850,39.250,40.000,39.450,38.950,37.750,33.850,30.400,25.700,25.400,25.600,28.150,32.400,31.850,31.350,31.200,31.100,31.950,32.450,35.200,38.400,35.850,30.700,27.850,26.900,26.650,25.250,24.450,22.500,22.050,20.000,19.750,19.100,18.500,18.400,17.400,16.900,16.800,16.450,16.050,16.300,17.450,19.300,20.000,21.050,22.800,22.550,23.300,24.050,23.100,23.100,22.500,20.800,19.550,18.800,18.200,17.650,17.750,17.150,16.550,16.200,16.000,15.600,15.150,15.150,16.250,17.800,19.150,21.000,22.800,23.850,24.250,26.200,25.650,25.050,23.850,23.600,23.100,22.950,22.550,21.550,20.450,19.600,18.700,18.300,18.000,17.550,17.300,17.200,17.950,19.450,21.100,23.050,24.650,25.050,25.850,25.300,26.650,25.500,25.900,26.250,25.300,25.150,23.600,22.050,21.700,21.150,20.550,20.500,20.200,20.500,20.600,20.900,21.700,22.000,22.250,23.400,23.900,25.250,26.200,26.000,25.300,25.200,25.300,25.500,25.350,25.050,24.850,24.050,23.150,22.300,21.900,21.150,20.300,19.650,19.700,19.750,20.250,21.500,23.600,24.600,25.900,25.450,24.850,25.900,26.150,26.250,26.350,26.250,25.850,25.300,24.600,23.750,22.250,21.750,21.450,21.500,21.300,21.250,21.200,21.600,22.000,23.650,25.200,26.400,25.500,25.150,26.950,28.350,25.650,25.000,25.500,24.150,22.900,21.600,21.750,21.500,21.550,20.450,19.500,18.750,18.650,18.200,17.300,17.900,18.050,17.400,16.850,17.950,20.550,21.950,22.600,22.300,22.400,22.300,21.100,20.250,19.200,18.900,18.600,18.350,17.700,17.200,16.850,16.900,16.800,16.800,16.600,16.350,17.200,18.350,19.550,20.300,21.600,21.800,23.300,23.200,24.550,24.950,24.900,23.700,22.000,19.650,18.250,17.700,17.250,16.900,16.550,16.050,16.450,15.400,14.900,14.700,16.100,18.450,19.800,23.000,25.250,27.600,27.900,28.550,29.450,29.700,29.350,27.000,23.550,21.900,20.750,20.150,19.600,19.150,18.800,18.550,18.200,17.750,17.650,17.800,18.750,19.600,20.450,21.950,23.700,23.150,24.150,24.550,21.400,19.150,19.050,16.500,15.900,14.850,15.300,14.100,13.800,13.600,13.450,13.400,13.050,12.750,12.800,12.750,13.600,14.950,16.100,17.500,18.500,19.300,19.400,19.750,19.400,19.450,19.450,18.900,17.650,16.800,15.900,15.050,14.550,14.250,13.800,13.850,13.700,13.650,13.350,13.400,14.050,15.000,16.650,17.850,18.450,18.200,18.900,19.850,20.000,19.700,18.800,17.500,16.600,16.250,16.000,16.300,16.400,15.800,15.850,14.600,14.650,15.200,14.900,14.600,15.150,16.000,16.350,17.000,18.300,19.050,19.300,19.400,18.650,18.750,19.100,18.300,17.950,17.550,16.900,16.450,15.850,15.800,15.650,15.200,14.700,14.950,15.250,15.200,15.800,16.800,17.900,19.700,21.050,21.600,22.550,22.750,22.900,22.500,21.950,20.450,19.600,19.200,18.000,16.950,16.450,16.150,15.600,15.150,15.250,15.200,14.750,15.050,15.600,17.750,18.450,20.050,21.350,22.500,23.550,24.100,22.600,23.150,24.100,22.650,21.250,19.900,19.100,18.250,17.750,17.500,16.600,16.100,15.850,15.750,15.700,16.350,19.600,25.750,27.800,30.050,32.350,31.900,32.450,29.600,28.850,23.450,21.100,20.100,20.100,19.900,19.300,19.050,18.850".split(",")).astype(np.float32)
num_forecast_steps = 24 * 7 * 2 # Two weeks.
demand_training_data = demand[:-num_forecast_steps]
colors = sns.color_palette()
c1, c2 = colors[0], colors[1]
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(2, 1, 1)
ax.plot(demand_dates[:-num_forecast_steps],
demand[:-num_forecast_steps], lw=2, label="training data")
ax.set_ylabel("Hourly demand (GW)")
ax = fig.add_subplot(2, 1, 2)
ax.plot(demand_dates[:-num_forecast_steps],
temperature[:-num_forecast_steps], lw=2, label="training data", c=c2)
ax.set_ylabel("Temperature (deg C)")
ax.set_title("Temperature")
ax.xaxis.set_major_locator(demand_loc)
ax.xaxis.set_major_formatter(demand_fmt)
fig.suptitle("Electricity Demand in Victoria, Australia (2014)",
fontsize=15)
fig.autofmt_xdate()
模型与拟合
我们的模型结合了一天中某个小时和一周中某一天的季节性、对温度影响进行建模的线性回归以及处理有界方差残差的自回归过程。
def build_model(observed_time_series):
hour_of_day_effect = sts.Seasonal(
num_seasons=24,
observed_time_series=observed_time_series,
name='hour_of_day_effect')
day_of_week_effect = sts.Seasonal(
num_seasons=7, num_steps_per_season=24,
observed_time_series=observed_time_series,
name='day_of_week_effect')
temperature_effect = sts.LinearRegression(
design_matrix=jnp.reshape(temperature - jnp.mean(temperature),
(-1, 1)), name='temperature_effect')
autoregressive = sts.Autoregressive(
order=1,
observed_time_series=observed_time_series,
name='autoregressive')
model = sts.Sum([hour_of_day_effect,
day_of_week_effect,
temperature_effect,
autoregressive],
observed_time_series=observed_time_series)
return model
如上所述,我们将使用变分推断拟合模型并从后验中绘制样本。
demand_model = build_model(demand_training_data)
# Build the variational surrogate posteriors `qs`.
# variational_posteriors = tfp.sts.build_factored_surrogate_posterior(
# model=demand_model)
init_fn, build_surrogate_fn = (
tfp.sts.build_factored_surrogate_posterior_stateless(model=demand_model))
Minimize the variational loss.
# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 200 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)
seed = tfp.random.sanitize_seed(jax.random.PRNGKey(42), salt='fit_stateless')
init_seed, fit_seed, sample_seed = tfp.random.split_seed(seed, n=3)
initial_parameters = init_fn(init_seed)
jd = demand_model.joint_distribution(demand_training_data)
# Build and optimize the variational loss function.
optimized_parameters, elbo_loss_curve = tfp.vi.fit_surrogate_posterior_stateless(
target_log_prob_fn=jd.log_prob,
initial_parameters=initial_parameters,
build_surrogate_posterior_fn=build_surrogate_fn,
optimizer=optax.adam(learning_rate=0.1),
num_steps=num_variational_steps,
seed=fit_seed)
plt.plot(elbo_loss_curve)
plt.show()
# Draw samples from the variational posterior.
surrogate_posterior = build_surrogate_fn(optimized_parameters)
q_samples_demand_ = surrogate_posterior.sample(50, seed=sample_seed)
print("Inferred parameters:")
for param in demand_model.parameters:
print("{}: {} +- {}".format(param.name,
jnp.mean(q_samples_demand_[param.name], axis=0),
jnp.std(q_samples_demand_[param.name], axis=0)))
Inferred parameters: observation_noise_scale: 0.007361860014498234 +- 0.001575619913637638 hour_of_day_effect_drift_scale: 0.002189201768487692 +- 0.0007748314528726041 day_of_week_effect_drift_scale: 0.01211678609251976 +- 0.018613168969750404 temperature_effect_weights: [0.06205687] +- [0.00406887] autoregressive_coefficients: [0.9839599] +- [0.00560341] autoregressive_level_scale: 0.14477692544460297 +- 0.003696543164551258
预测与驳斥
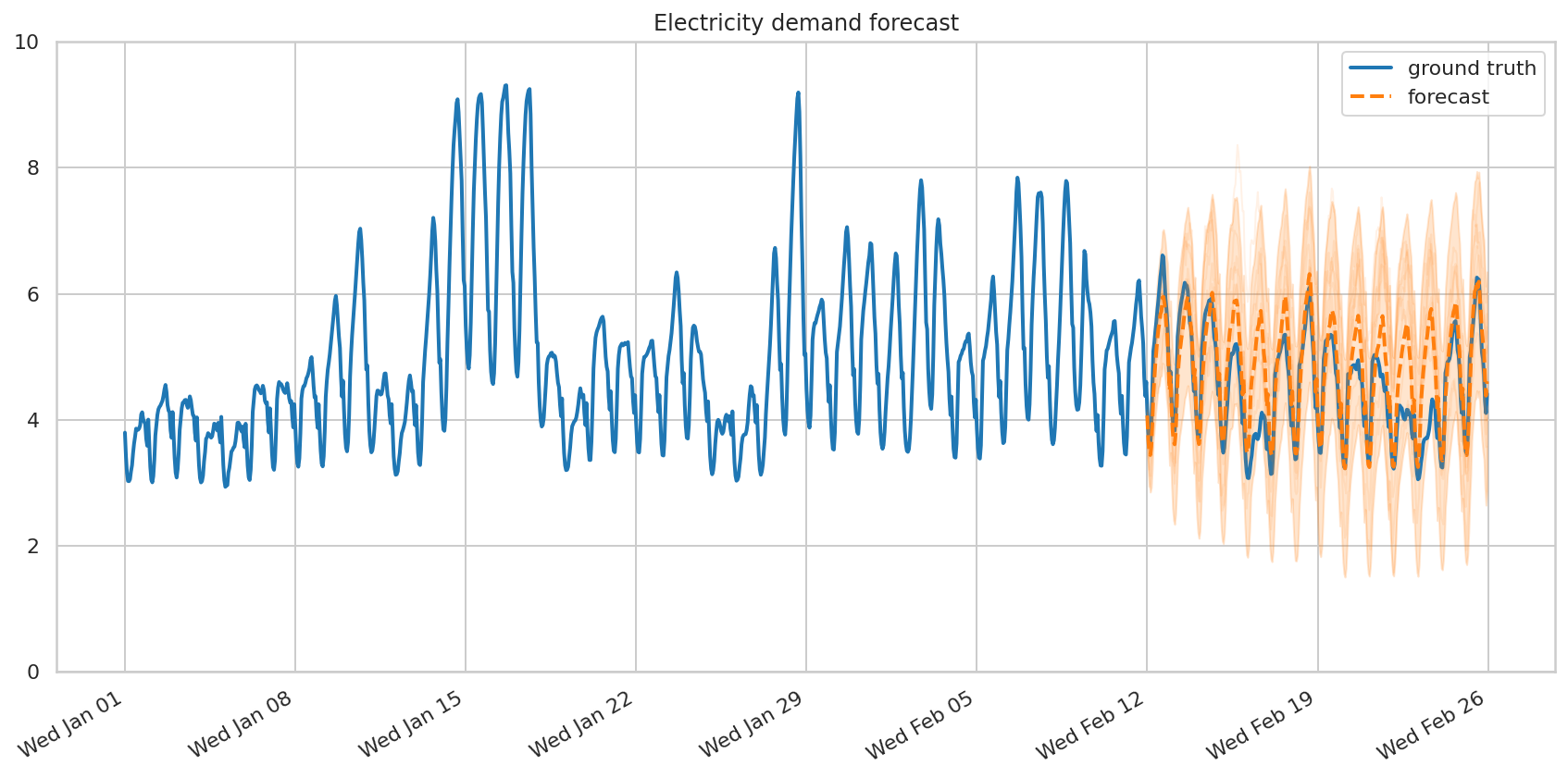
同样,我们只需要使用我们的模型、时间序列和采样参数调用 tfp.sts.forecast 来创建预测。
demand_forecast_dist = tfp.sts.forecast(
model=demand_model,
observed_time_series=demand_training_data,
parameter_samples=q_samples_demand_,
num_steps_forecast=num_forecast_steps)
num_samples=10
demand_forecast_mean = demand_forecast_dist.mean()[..., 0]
demand_forecast_scale = demand_forecast_dist.stddev()[..., 0]
demand_forecast_samples =demand_forecast_dist.sample(
num_samples, seed=sample_seed)[..., 0]
fig, ax = plot_forecast(demand_dates, demand,
demand_forecast_mean,
demand_forecast_scale,
demand_forecast_samples,
title="Electricity demand forecast",
x_locator=demand_loc, x_formatter=demand_fmt)
ax.set_ylim([0, 10])
fig.tight_layout()
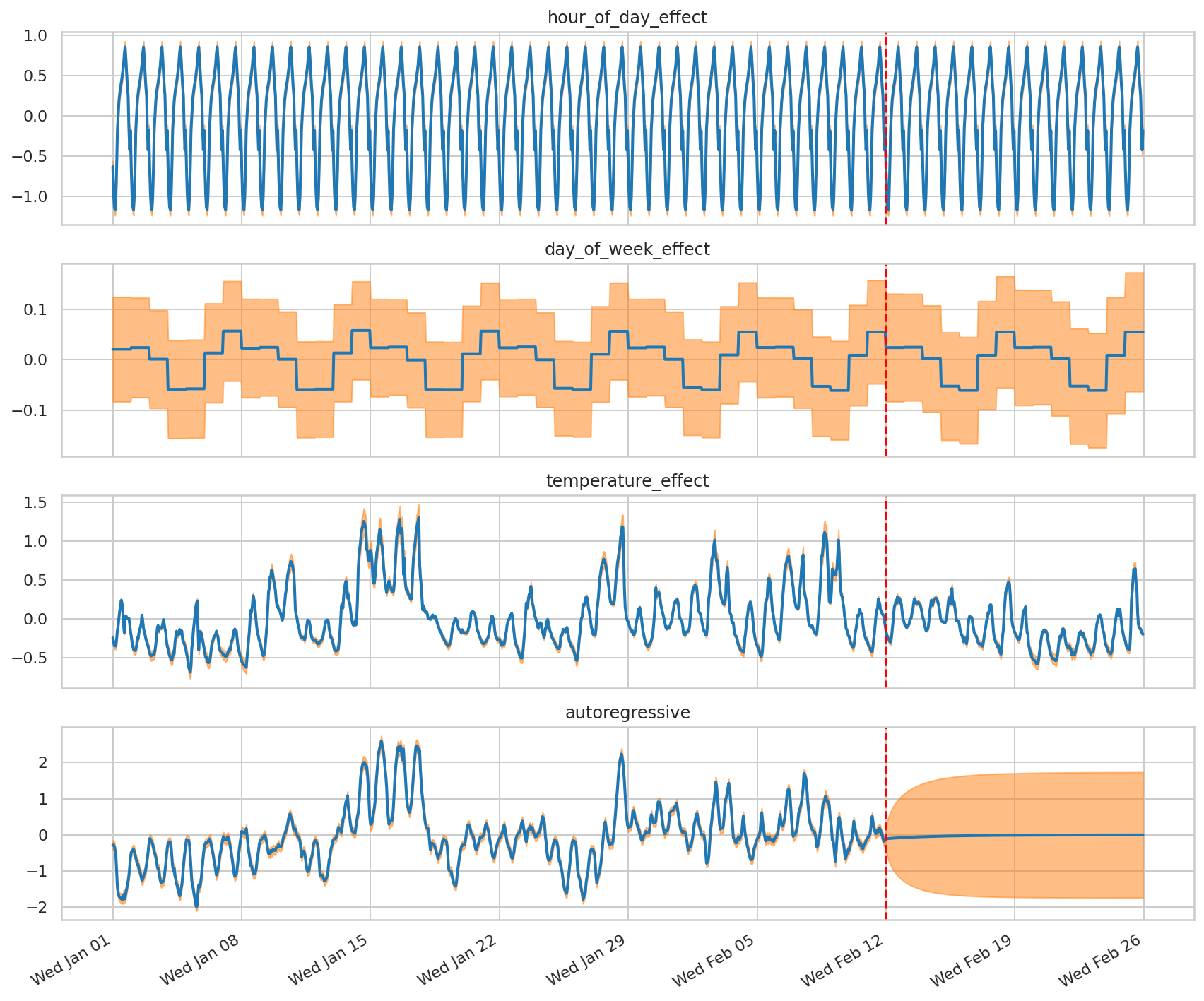
我们将观测到和预测的序列的分解呈现为各个组件:
# Get the distributions over component outputs from the posterior marginals on
# training data, and from the forecast model.
component_dists = sts.decompose_by_component(
demand_model,
observed_time_series=demand_training_data,
parameter_samples=q_samples_demand_)
forecast_component_dists = sts.decompose_forecast_by_component(
demand_model,
forecast_dist=demand_forecast_dist,
parameter_samples=q_samples_demand_)
demand_component_means_, demand_component_stddevs_ = (
{k.name: c.mean() for k, c in component_dists.items()},
{k.name: c.stddev() for k, c in component_dists.items()})
(
demand_forecast_component_means_,
demand_forecast_component_stddevs_
) = (
{k.name: c.mean() for k, c in forecast_component_dists.items()},
{k.name: c.stddev() for k, c in forecast_component_dists.items()}
)
# Concatenate the training data with forecasts for plotting.
component_with_forecast_means_ = collections.OrderedDict()
component_with_forecast_stddevs_ = collections.OrderedDict()
for k in demand_component_means_.keys():
component_with_forecast_means_[k] = jnp.concatenate([
demand_component_means_[k],
demand_forecast_component_means_[k]], axis=-1)
component_with_forecast_stddevs_[k] = jnp.concatenate([
demand_component_stddevs_[k],
demand_forecast_component_stddevs_[k]], axis=-1)
fig, axes = plot_components(
demand_dates,
component_with_forecast_means_,
component_with_forecast_stddevs_,
x_locator=demand_loc, x_formatter=demand_fmt)
for ax in axes.values():
ax.axvline(demand_dates[-num_forecast_steps], linestyle="--", color='red')
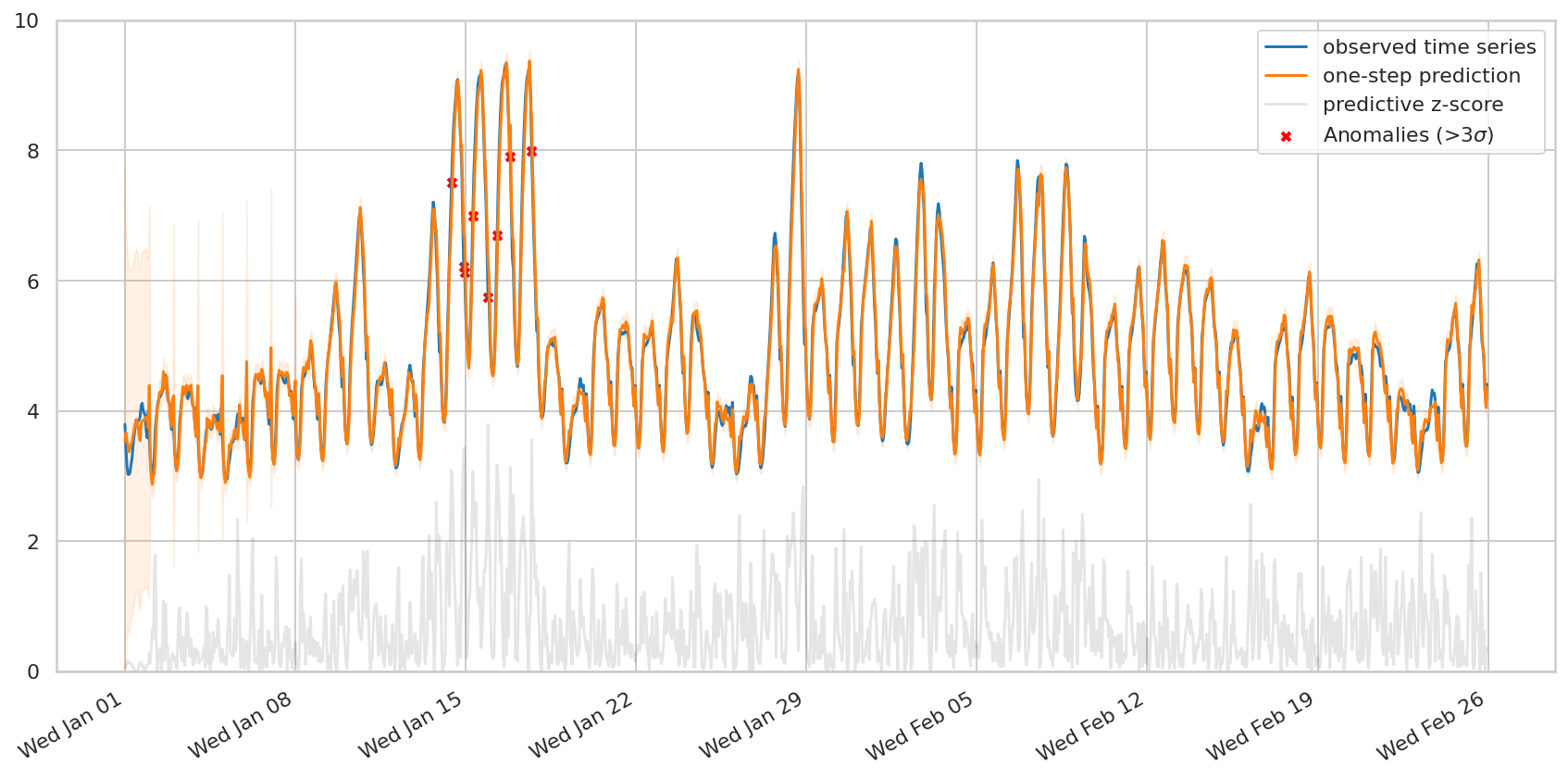
如果我们想检测观测到的序列中的异常,可能还会对一步预测分布感兴趣:每个时间步骤的预测,只给出到该点的时间步骤。tfp.sts.one_step_predictive 一次可以计算所有一步预测分布:
demand_one_step_dist = sts.one_step_predictive(
demand_model,
observed_time_series=demand,
parameter_samples=q_samples_demand_)
demand_one_step_mean, demand_one_step_scale = (
demand_one_step_dist.mean(), demand_one_step_dist.stddev())
一种简单的异常检测方案是标记所有时间步骤,其中观测值与预测值之间相差超过三个标准偏差 – 根据模型,这些是最“令人惊讶的”时间步骤。
fig, ax = plot_one_step_predictive(
demand_dates, demand,
demand_one_step_mean, demand_one_step_scale,
x_locator=demand_loc, x_formatter=demand_fmt)
ax.set_ylim(0, 10)
# Use the one-step-ahead forecasts to detect anomalous timesteps.
zscores = jnp.abs((demand - demand_one_step_mean) /
demand_one_step_scale)
anomalies = zscores > 3.0
ax.scatter(demand_dates[anomalies],
demand[anomalies],
c="red", marker="x", s=20, linewidth=2, label=r"Anomalies (>3$\sigma$)")
ax.plot(demand_dates, zscores, color="black", alpha=0.1, label='predictive z-score')
ax.legend()
plt.show()