הצג באתר TensorFlow.org הצג באתר TensorFlow.org |  הפעל בגוגל קולאב הפעל בגוגל קולאב |  צפה במקור ב-GitHub צפה במקור ב-GitHub |  הורד מחברת הורד מחברת |
בדוגמה זו אנו מראים כיצד להתאים מודלים של רגרסיה באמצעות "שכבות הסתברותיות" של TFP.
תלות ותנאים מוקדמים
יְבוּא
from pprint import pprint
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
sns.reset_defaults()
#sns.set_style('whitegrid')
#sns.set_context('talk')
sns.set_context(context='talk',font_scale=0.7)
%matplotlib inline
tfd = tfp.distributions
הפוך דברים מהר!
לפני שנצלול פנימה, בואו נוודא שאנחנו משתמשים ב-GPU עבור הדגמה זו.
כדי לעשות זאת, בחר "זמן ריצה" -> "שנה סוג זמן ריצה" -> "מאיץ חומרה" -> "GPU".
הקטע הבא יאמת שיש לנו גישה ל-GPU.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
WARNING: GPU device not found.
מוֹטִיבָצִיָה
האם זה לא יהיה נהדר אם נוכל להשתמש ב-TFP כדי לציין מודל הסתברותי ואז פשוט למזער את סבירות היומן השליליות, כלומר,
negloglik = lambda y, rv_y: -rv_y.log_prob(y)
ובכן, לא רק שזה אפשרי, אלא שהקולאב הזה מראה איך! (בהקשר של בעיות רגרסיה לינארית.)
סנתז מערך נתונים.
w0 = 0.125
b0 = 5.
x_range = [-20, 60]
def load_dataset(n=150, n_tst=150):
np.random.seed(43)
def s(x):
g = (x - x_range[0]) / (x_range[1] - x_range[0])
return 3 * (0.25 + g**2.)
x = (x_range[1] - x_range[0]) * np.random.rand(n) + x_range[0]
eps = np.random.randn(n) * s(x)
y = (w0 * x * (1. + np.sin(x)) + b0) + eps
x = x[..., np.newaxis]
x_tst = np.linspace(*x_range, num=n_tst).astype(np.float32)
x_tst = x_tst[..., np.newaxis]
return y, x, x_tst
y, x, x_tst = load_dataset()
מקרה 1: אין אי ודאות
# Build model.
model = tf.keras.Sequential([
tf.keras.layers.Dense(1),
tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
0.13032457 5.13029
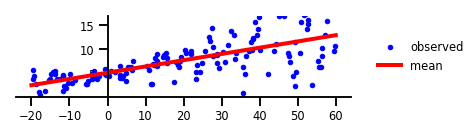
איור 1: אין אי ודאות.
w = np.squeeze(model.layers[-2].kernel.numpy())
b = np.squeeze(model.layers[-2].bias.numpy())
plt.figure(figsize=[6, 1.5]) # inches
#plt.figure(figsize=[8, 5]) # inches
plt.plot(x, y, 'b.', label='observed');
plt.plot(x_tst, yhat.mean(),'r', label='mean', linewidth=4);
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig1.png', bbox_inches='tight', dpi=300)
מקרה 2: אי ודאות אליאטורית
# Build model.
model = tf.keras.Sequential([
tf.keras.layers.Dense(1 + 1),
tfp.layers.DistributionLambda(
lambda t: tfd.Normal(loc=t[..., :1],
scale=1e-3 + tf.math.softplus(0.05 * t[...,1:]))),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
[0.14738432 0.1815331 ] [4.4812164 1.2219843]
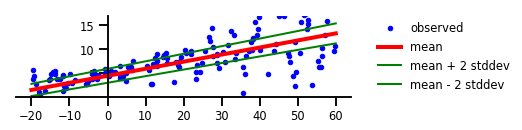
איור 2: אי ודאות אליאטורית
plt.figure(figsize=[6, 1.5]) # inches
plt.plot(x, y, 'b.', label='observed');
m = yhat.mean()
s = yhat.stddev()
plt.plot(x_tst, m, 'r', linewidth=4, label='mean');
plt.plot(x_tst, m + 2 * s, 'g', linewidth=2, label=r'mean + 2 stddev');
plt.plot(x_tst, m - 2 * s, 'g', linewidth=2, label=r'mean - 2 stddev');
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig2.png', bbox_inches='tight', dpi=300)
מקרה 3: אי ודאות אפיסטמית
# Specify the surrogate posterior over `keras.layers.Dense` `kernel` and `bias`.
def posterior_mean_field(kernel_size, bias_size=0, dtype=None):
n = kernel_size + bias_size
c = np.log(np.expm1(1.))
return tf.keras.Sequential([
tfp.layers.VariableLayer(2 * n, dtype=dtype),
tfp.layers.DistributionLambda(lambda t: tfd.Independent(
tfd.Normal(loc=t[..., :n],
scale=1e-5 + tf.nn.softplus(c + t[..., n:])),
reinterpreted_batch_ndims=1)),
])
# Specify the prior over `keras.layers.Dense` `kernel` and `bias`.
def prior_trainable(kernel_size, bias_size=0, dtype=None):
n = kernel_size + bias_size
return tf.keras.Sequential([
tfp.layers.VariableLayer(n, dtype=dtype),
tfp.layers.DistributionLambda(lambda t: tfd.Independent(
tfd.Normal(loc=t, scale=1),
reinterpreted_batch_ndims=1)),
])
# Build model.
model = tf.keras.Sequential([
tfp.layers.DenseVariational(1, posterior_mean_field, prior_trainable, kl_weight=1/x.shape[0]),
tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
[ 0.1387333 5.125723 -4.112224 -2.2171402] [0.12476114 5.147452 ]
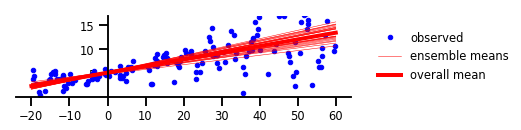
איור 3: אי ודאות אפיסטמית
plt.figure(figsize=[6, 1.5]) # inches
plt.clf();
plt.plot(x, y, 'b.', label='observed');
yhats = [model(x_tst) for _ in range(100)]
avgm = np.zeros_like(x_tst[..., 0])
for i, yhat in enumerate(yhats):
m = np.squeeze(yhat.mean())
s = np.squeeze(yhat.stddev())
if i < 25:
plt.plot(x_tst, m, 'r', label='ensemble means' if i == 0 else None, linewidth=0.5)
avgm += m
plt.plot(x_tst, avgm/len(yhats), 'r', label='overall mean', linewidth=4)
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig3.png', bbox_inches='tight', dpi=300)
מקרה 4: אי ודאות אליאטורית ואפיסטמית
# Build model.
model = tf.keras.Sequential([
tfp.layers.DenseVariational(1 + 1, posterior_mean_field, prior_trainable, kl_weight=1/x.shape[0]),
tfp.layers.DistributionLambda(
lambda t: tfd.Normal(loc=t[..., :1],
scale=1e-3 + tf.math.softplus(0.01 * t[...,1:]))),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);
# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
[ 0.12753433 2.7504077 5.160624 3.8251898 -3.4283297 -0.8961645 -2.2378397 0.1496858 ] [0.14511648 2.7104297 5.1248145 3.7724588 ]
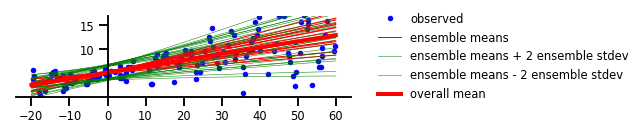
איור 4: אי-ודאות אליאטורית וגם אפיסטמית
plt.figure(figsize=[6, 1.5]) # inches
plt.plot(x, y, 'b.', label='observed');
yhats = [model(x_tst) for _ in range(100)]
avgm = np.zeros_like(x_tst[..., 0])
for i, yhat in enumerate(yhats):
m = np.squeeze(yhat.mean())
s = np.squeeze(yhat.stddev())
if i < 15:
plt.plot(x_tst, m, 'r', label='ensemble means' if i == 0 else None, linewidth=1.)
plt.plot(x_tst, m + 2 * s, 'g', linewidth=0.5, label='ensemble means + 2 ensemble stdev' if i == 0 else None);
plt.plot(x_tst, m - 2 * s, 'g', linewidth=0.5, label='ensemble means - 2 ensemble stdev' if i == 0 else None);
avgm += m
plt.plot(x_tst, avgm/len(yhats), 'r', label='overall mean', linewidth=4)
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig4.png', bbox_inches='tight', dpi=300)
מקרה 5: אי ודאות תפקודית
ליבת PSD מותאמת אישית
class RBFKernelFn(tf.keras.layers.Layer):
def __init__(self, **kwargs):
super(RBFKernelFn, self).__init__(**kwargs)
dtype = kwargs.get('dtype', None)
self._amplitude = self.add_variable(
initializer=tf.constant_initializer(0),
dtype=dtype,
name='amplitude')
self._length_scale = self.add_variable(
initializer=tf.constant_initializer(0),
dtype=dtype,
name='length_scale')
def call(self, x):
# Never called -- this is just a layer so it can hold variables
# in a way Keras understands.
return x
@property
def kernel(self):
return tfp.math.psd_kernels.ExponentiatedQuadratic(
amplitude=tf.nn.softplus(0.1 * self._amplitude),
length_scale=tf.nn.softplus(5. * self._length_scale)
)
# For numeric stability, set the default floating-point dtype to float64
tf.keras.backend.set_floatx('float64')
# Build model.
num_inducing_points = 40
model = tf.keras.Sequential([
tf.keras.layers.InputLayer(input_shape=[1]),
tf.keras.layers.Dense(1, kernel_initializer='ones', use_bias=False),
tfp.layers.VariationalGaussianProcess(
num_inducing_points=num_inducing_points,
kernel_provider=RBFKernelFn(),
event_shape=[1],
inducing_index_points_initializer=tf.constant_initializer(
np.linspace(*x_range, num=num_inducing_points,
dtype=x.dtype)[..., np.newaxis]),
unconstrained_observation_noise_variance_initializer=(
tf.constant_initializer(np.array(0.54).astype(x.dtype))),
),
])
# Do inference.
batch_size = 32
loss = lambda y, rv_y: rv_y.variational_loss(
y, kl_weight=np.array(batch_size, x.dtype) / x.shape[0])
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=loss)
model.fit(x, y, batch_size=batch_size, epochs=1000, verbose=False)
# Profit.
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)
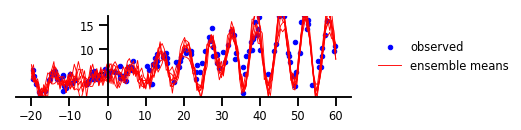
איור 5: אי ודאות תפקודית
y, x, _ = load_dataset()
plt.figure(figsize=[6, 1.5]) # inches
plt.plot(x, y, 'b.', label='observed');
num_samples = 7
for i in range(num_samples):
sample_ = yhat.sample().numpy()
plt.plot(x_tst,
sample_[..., 0].T,
'r',
linewidth=0.9,
label='ensemble means' if i == 0 else None);
plt.ylim(-0.,17);
plt.yticks(np.linspace(0, 15, 4)[1:]);
plt.xticks(np.linspace(*x_range, num=9));
ax=plt.gca();
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
#ax.spines['left'].set_smart_bounds(True)
#ax.spines['bottom'].set_smart_bounds(True)
plt.legend(loc='center left', fancybox=True, framealpha=0., bbox_to_anchor=(1.05, 0.5))
plt.savefig('/tmp/fig5.png', bbox_inches='tight', dpi=300)