 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
W tym samouczku zaimplementowano uproszczoną Quantum Convolutional Neural Network (QCNN), proponowany kwantowy odpowiednik klasycznej konwolucyjnej sieci neuronowej, która jest również translacyjna niezmienna .
Ten przykład pokazuje, jak wykryć określone właściwości źródła danych kwantowych, takie jak czujnik kwantowy lub złożona symulacja z urządzenia. Źródłem danych kwantowych jest stan klastra, który może, ale nie musi, mieć wzbudzenie — to, co QCNN nauczy się wykrywać (zestaw danych użyty w artykule to klasyfikacja fazy SPT).
Ustawiać
pip install tensorflow==2.7.0
Zainstaluj TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Teraz zaimportuj TensorFlow i zależności modułu:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:43:45.380301: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Zbuduj QCNN
1.1 Składanie obwodów na wykresie TensorFlow
TensorFlow Quantum (TFQ) zapewnia klasy warstw zaprojektowane do budowy obwodów w grafie. Jednym z przykładów jest warstwa tfq.layers.AddCircuit , która dziedziczy po tf.keras.Layer . Ta warstwa może być dołączana do wejściowej partii obwodów lub dołączana do niej, jak pokazano na poniższym rysunku.

Poniższy fragment kodu używa tej warstwy:
qubit = cirq.GridQubit(0, 0)
# Define some circuits.
circuit1 = cirq.Circuit(cirq.X(qubit))
circuit2 = cirq.Circuit(cirq.H(qubit))
# Convert to a tensor.
input_circuit_tensor = tfq.convert_to_tensor([circuit1, circuit2])
# Define a circuit that we want to append
y_circuit = cirq.Circuit(cirq.Y(qubit))
# Instantiate our layer
y_appender = tfq.layers.AddCircuit()
# Run our circuit tensor through the layer and save the output.
output_circuit_tensor = y_appender(input_circuit_tensor, append=y_circuit)
Sprawdź tensor wejściowy:
print(tfq.from_tensor(input_circuit_tensor))
[cirq.Circuit([
cirq.Moment(
cirq.X(cirq.GridQubit(0, 0)),
),
])
cirq.Circuit([
cirq.Moment(
cirq.H(cirq.GridQubit(0, 0)),
),
]) ]
I przyjrzyj się tensorowi wyjściowemu:
print(tfq.from_tensor(output_circuit_tensor))
[cirq.Circuit([
cirq.Moment(
cirq.X(cirq.GridQubit(0, 0)),
),
cirq.Moment(
cirq.Y(cirq.GridQubit(0, 0)),
),
])
cirq.Circuit([
cirq.Moment(
cirq.H(cirq.GridQubit(0, 0)),
),
cirq.Moment(
cirq.Y(cirq.GridQubit(0, 0)),
),
]) ]
Chociaż możliwe jest uruchomienie poniższych przykładów bez użycia tfq.layers.AddCircuit , jest to dobra okazja, aby zrozumieć, jak złożoną funkcjonalność można osadzić w wykresach obliczeniowych TensorFlow.
1.2 Przegląd problemów
Przygotujesz stan klastra i wytrenujesz klasyfikator kwantowy, aby wykryć, czy jest „podekscytowany”, czy nie. Stan klastra jest mocno powikłany, ale niekoniecznie trudny dla klasycznego komputera. Dla jasności jest to prostszy zbiór danych niż ten użyty w artykule.
W tym zadaniu klasyfikacyjnym zaimplementujesz głęboką architekturę QCNN podobną do MERA , ponieważ:
- Podobnie jak QCNN, stan klastra w pierścieniu jest translacyjny niezmienny.
- Stan klastra jest mocno uwikłany.
Ta architektura powinna skutecznie zmniejszać splątanie, uzyskując klasyfikację poprzez odczytanie pojedynczego kubitu.

„Podekscytowany” stan klastra jest definiowany jako stan klastra, w którym do dowolnego z kubitów zastosowano bramkę cirq.rx Qconv i QPool są omówione w dalszej części tego samouczka.
1.3 Bloki konstrukcyjne dla TensorFlow

Jednym ze sposobów rozwiązania tego problemu za pomocą TensorFlow Quantum jest wdrożenie następujących elementów:
- Dane wejściowe do modelu to tensor obwodu — albo pusty obwód, albo bramka X na określonym kubicie wskazująca na wzbudzenie.
- Pozostałe komponenty kwantowe modelu są konstruowane za pomocą warstw
tfq.layers.AddCircuit. - Do wnioskowania używana jest warstwa
tfq.layers.PQC. To odczytuje \(\langle \hat{Z} \rangle\) i porównuje go z etykietą 1 dla stanu wzbudzonego lub -1 dla stanu niewzbudzonego.
1.4 Dane
Przed zbudowaniem modelu możesz wygenerować swoje dane. W tym przypadku będzie to wzbudzanie stanu klastra (oryginalny artykuł używa bardziej skomplikowanego zestawu danych). Wzbudzenia są reprezentowane przez bramki cirq.rx Wystarczająco duży obrót jest uważany za wzbudzenie i jest oznaczony jako 1 , a obrót, który nie jest wystarczająco duży, jest oznaczony jako -1 i nie jest uważany za wzbudzenie.
def generate_data(qubits):
"""Generate training and testing data."""
n_rounds = 20 # Produces n_rounds * n_qubits datapoints.
excitations = []
labels = []
for n in range(n_rounds):
for bit in qubits:
rng = np.random.uniform(-np.pi, np.pi)
excitations.append(cirq.Circuit(cirq.rx(rng)(bit)))
labels.append(1 if (-np.pi / 2) <= rng <= (np.pi / 2) else -1)
split_ind = int(len(excitations) * 0.7)
train_excitations = excitations[:split_ind]
test_excitations = excitations[split_ind:]
train_labels = labels[:split_ind]
test_labels = labels[split_ind:]
return tfq.convert_to_tensor(train_excitations), np.array(train_labels), \
tfq.convert_to_tensor(test_excitations), np.array(test_labels)
Widać, że podobnie jak w przypadku zwykłego uczenia maszynowego, tworzysz zestaw treningowy i testowy, który posłuży do porównania modelu. Możesz szybko spojrzeć na niektóre punkty danych za pomocą:
sample_points, sample_labels, _, __ = generate_data(cirq.GridQubit.rect(1, 4))
print('Input:', tfq.from_tensor(sample_points)[0], 'Output:', sample_labels[0])
print('Input:', tfq.from_tensor(sample_points)[1], 'Output:', sample_labels[1])
Input: (0, 0): ───X^0.449─── Output: 1 Input: (0, 1): ───X^-0.74─── Output: -1
1.5 Zdefiniuj warstwy
Teraz zdefiniuj warstwy pokazane na powyższym rysunku w TensorFlow.
1.5.1 Stan klastra
Pierwszym krokiem jest zdefiniowanie stanu klastra za pomocą Cirq , dostarczonej przez Google platformy do programowania obwodów kwantowych. Ponieważ jest to statyczna część modelu, osadź ją za pomocą funkcji tfq.layers.AddCircuit .
def cluster_state_circuit(bits):
"""Return a cluster state on the qubits in `bits`."""
circuit = cirq.Circuit()
circuit.append(cirq.H.on_each(bits))
for this_bit, next_bit in zip(bits, bits[1:] + [bits[0]]):
circuit.append(cirq.CZ(this_bit, next_bit))
return circuit
Wyświetl obwód stanu klastra dla prostokąta cirq.GridQubit s:
SVGCircuit(cluster_state_circuit(cirq.GridQubit.rect(1, 4)))
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
1.5.2 Warstwy QCNN
Zdefiniuj warstwy, które składają się na model, korzystając z papieru Cong i Lukin QCNN . Istnieje kilka warunków wstępnych:
- Jedno- i dwukubitowe sparametryzowane macierze unitarne z papieru Tucciego .
- Ogólna sparametryzowana operacja pulowania dwóch kubitów.
def one_qubit_unitary(bit, symbols):
"""Make a Cirq circuit enacting a rotation of the bloch sphere about the X,
Y and Z axis, that depends on the values in `symbols`.
"""
return cirq.Circuit(
cirq.X(bit)**symbols[0],
cirq.Y(bit)**symbols[1],
cirq.Z(bit)**symbols[2])
def two_qubit_unitary(bits, symbols):
"""Make a Cirq circuit that creates an arbitrary two qubit unitary."""
circuit = cirq.Circuit()
circuit += one_qubit_unitary(bits[0], symbols[0:3])
circuit += one_qubit_unitary(bits[1], symbols[3:6])
circuit += [cirq.ZZ(*bits)**symbols[6]]
circuit += [cirq.YY(*bits)**symbols[7]]
circuit += [cirq.XX(*bits)**symbols[8]]
circuit += one_qubit_unitary(bits[0], symbols[9:12])
circuit += one_qubit_unitary(bits[1], symbols[12:])
return circuit
def two_qubit_pool(source_qubit, sink_qubit, symbols):
"""Make a Cirq circuit to do a parameterized 'pooling' operation, which
attempts to reduce entanglement down from two qubits to just one."""
pool_circuit = cirq.Circuit()
sink_basis_selector = one_qubit_unitary(sink_qubit, symbols[0:3])
source_basis_selector = one_qubit_unitary(source_qubit, symbols[3:6])
pool_circuit.append(sink_basis_selector)
pool_circuit.append(source_basis_selector)
pool_circuit.append(cirq.CNOT(control=source_qubit, target=sink_qubit))
pool_circuit.append(sink_basis_selector**-1)
return pool_circuit
Aby zobaczyć, co stworzyłeś, wydrukuj jednokubitowy obwód unitarny:
SVGCircuit(one_qubit_unitary(cirq.GridQubit(0, 0), sympy.symbols('x0:3')))
I dwukubitowy obwód unitarny:
SVGCircuit(two_qubit_unitary(cirq.GridQubit.rect(1, 2), sympy.symbols('x0:15')))
Oraz dwukubitowy obwód pulowania:
SVGCircuit(two_qubit_pool(*cirq.GridQubit.rect(1, 2), sympy.symbols('x0:6')))
1.5.2.1 Splot kwantowy
Podobnie jak w artykule Conga i Lukina , zdefiniuj jednowymiarowy splot kwantowy jako zastosowanie sparametryzowanej unitarnej dwóch kubitów do każdej pary sąsiednich kubitów z krokiem równym jeden.
def quantum_conv_circuit(bits, symbols):
"""Quantum Convolution Layer following the above diagram.
Return a Cirq circuit with the cascade of `two_qubit_unitary` applied
to all pairs of qubits in `bits` as in the diagram above.
"""
circuit = cirq.Circuit()
for first, second in zip(bits[0::2], bits[1::2]):
circuit += two_qubit_unitary([first, second], symbols)
for first, second in zip(bits[1::2], bits[2::2] + [bits[0]]):
circuit += two_qubit_unitary([first, second], symbols)
return circuit
Wyświetl (bardzo poziomy) obwód:
SVGCircuit(
quantum_conv_circuit(cirq.GridQubit.rect(1, 8), sympy.symbols('x0:15')))
1.5.2.2 Pule kwantowe
Warstwa puli kwantowej tworzy pule od \(N\) do \(\frac{N}{2}\) przy użyciu zdefiniowanej powyżej puli dwóch kubitów.
def quantum_pool_circuit(source_bits, sink_bits, symbols):
"""A layer that specifies a quantum pooling operation.
A Quantum pool tries to learn to pool the relevant information from two
qubits onto 1.
"""
circuit = cirq.Circuit()
for source, sink in zip(source_bits, sink_bits):
circuit += two_qubit_pool(source, sink, symbols)
return circuit
Zbadaj obwód komponentu puli:
test_bits = cirq.GridQubit.rect(1, 8)
SVGCircuit(
quantum_pool_circuit(test_bits[:4], test_bits[4:], sympy.symbols('x0:6')))
1.6 Definicja modelu
Teraz użyj zdefiniowanych warstw do skonstruowania czysto kwantowego CNN. Zacznij od ośmiu kubitów, zmniejsz pulę do jednego, a następnie zmierz \(\langle \hat{Z} \rangle\).
def create_model_circuit(qubits):
"""Create sequence of alternating convolution and pooling operators
which gradually shrink over time."""
model_circuit = cirq.Circuit()
symbols = sympy.symbols('qconv0:63')
# Cirq uses sympy.Symbols to map learnable variables. TensorFlow Quantum
# scans incoming circuits and replaces these with TensorFlow variables.
model_circuit += quantum_conv_circuit(qubits, symbols[0:15])
model_circuit += quantum_pool_circuit(qubits[:4], qubits[4:],
symbols[15:21])
model_circuit += quantum_conv_circuit(qubits[4:], symbols[21:36])
model_circuit += quantum_pool_circuit(qubits[4:6], qubits[6:],
symbols[36:42])
model_circuit += quantum_conv_circuit(qubits[6:], symbols[42:57])
model_circuit += quantum_pool_circuit([qubits[6]], [qubits[7]],
symbols[57:63])
return model_circuit
# Create our qubits and readout operators in Cirq.
cluster_state_bits = cirq.GridQubit.rect(1, 8)
readout_operators = cirq.Z(cluster_state_bits[-1])
# Build a sequential model enacting the logic in 1.3 of this notebook.
# Here you are making the static cluster state prep as a part of the AddCircuit and the
# "quantum datapoints" are coming in the form of excitation
excitation_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
cluster_state = tfq.layers.AddCircuit()(
excitation_input, prepend=cluster_state_circuit(cluster_state_bits))
quantum_model = tfq.layers.PQC(create_model_circuit(cluster_state_bits),
readout_operators)(cluster_state)
qcnn_model = tf.keras.Model(inputs=[excitation_input], outputs=[quantum_model])
# Show the keras plot of the model
tf.keras.utils.plot_model(qcnn_model,
show_shapes=True,
show_layer_names=False,
dpi=70)

1.7 Trenuj modelkę
Trenuj model na całej partii, aby uprościć ten przykład.
# Generate some training data.
train_excitations, train_labels, test_excitations, test_labels = generate_data(
cluster_state_bits)
# Custom accuracy metric.
@tf.function
def custom_accuracy(y_true, y_pred):
y_true = tf.squeeze(y_true)
y_pred = tf.map_fn(lambda x: 1.0 if x >= 0 else -1.0, y_pred)
return tf.keras.backend.mean(tf.keras.backend.equal(y_true, y_pred))
qcnn_model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.losses.mse,
metrics=[custom_accuracy])
history = qcnn_model.fit(x=train_excitations,
y=train_labels,
batch_size=16,
epochs=25,
verbose=1,
validation_data=(test_excitations, test_labels))
Epoch 1/25 7/7 [==============================] - 2s 176ms/step - loss: 0.8961 - custom_accuracy: 0.7143 - val_loss: 0.8012 - val_custom_accuracy: 0.7500 Epoch 2/25 7/7 [==============================] - 1s 140ms/step - loss: 0.7736 - custom_accuracy: 0.7946 - val_loss: 0.7355 - val_custom_accuracy: 0.8542 Epoch 3/25 7/7 [==============================] - 1s 138ms/step - loss: 0.7319 - custom_accuracy: 0.8393 - val_loss: 0.7045 - val_custom_accuracy: 0.8125 Epoch 4/25 7/7 [==============================] - 1s 137ms/step - loss: 0.6976 - custom_accuracy: 0.8482 - val_loss: 0.6829 - val_custom_accuracy: 0.8333 Epoch 5/25 7/7 [==============================] - 1s 143ms/step - loss: 0.6696 - custom_accuracy: 0.8750 - val_loss: 0.6749 - val_custom_accuracy: 0.7917 Epoch 6/25 7/7 [==============================] - 1s 137ms/step - loss: 0.6631 - custom_accuracy: 0.8750 - val_loss: 0.6718 - val_custom_accuracy: 0.7917 Epoch 7/25 7/7 [==============================] - 1s 135ms/step - loss: 0.6536 - custom_accuracy: 0.8929 - val_loss: 0.6638 - val_custom_accuracy: 0.8750 Epoch 8/25 7/7 [==============================] - 1s 141ms/step - loss: 0.6376 - custom_accuracy: 0.8750 - val_loss: 0.6311 - val_custom_accuracy: 0.8542 Epoch 9/25 7/7 [==============================] - 1s 137ms/step - loss: 0.6208 - custom_accuracy: 0.8750 - val_loss: 0.5995 - val_custom_accuracy: 0.8542 Epoch 10/25 7/7 [==============================] - 1s 134ms/step - loss: 0.5887 - custom_accuracy: 0.8661 - val_loss: 0.5655 - val_custom_accuracy: 0.8333 Epoch 11/25 7/7 [==============================] - 1s 144ms/step - loss: 0.5796 - custom_accuracy: 0.8482 - val_loss: 0.5681 - val_custom_accuracy: 0.8333 Epoch 12/25 7/7 [==============================] - 1s 143ms/step - loss: 0.5630 - custom_accuracy: 0.7946 - val_loss: 0.5179 - val_custom_accuracy: 0.8333 Epoch 13/25 7/7 [==============================] - 1s 137ms/step - loss: 0.5405 - custom_accuracy: 0.8304 - val_loss: 0.5003 - val_custom_accuracy: 0.8333 Epoch 14/25 7/7 [==============================] - 1s 138ms/step - loss: 0.5259 - custom_accuracy: 0.8036 - val_loss: 0.4787 - val_custom_accuracy: 0.8333 Epoch 15/25 7/7 [==============================] - 1s 137ms/step - loss: 0.5077 - custom_accuracy: 0.8482 - val_loss: 0.4741 - val_custom_accuracy: 0.8125 Epoch 16/25 7/7 [==============================] - 1s 136ms/step - loss: 0.5082 - custom_accuracy: 0.8214 - val_loss: 0.4739 - val_custom_accuracy: 0.8125 Epoch 17/25 7/7 [==============================] - 1s 137ms/step - loss: 0.5138 - custom_accuracy: 0.8214 - val_loss: 0.4859 - val_custom_accuracy: 0.8750 Epoch 18/25 7/7 [==============================] - 1s 133ms/step - loss: 0.5073 - custom_accuracy: 0.8304 - val_loss: 0.4879 - val_custom_accuracy: 0.8333 Epoch 19/25 7/7 [==============================] - 1s 138ms/step - loss: 0.5084 - custom_accuracy: 0.8304 - val_loss: 0.4745 - val_custom_accuracy: 0.8542 Epoch 20/25 7/7 [==============================] - 1s 139ms/step - loss: 0.5057 - custom_accuracy: 0.8571 - val_loss: 0.4702 - val_custom_accuracy: 0.8333 Epoch 21/25 7/7 [==============================] - 1s 135ms/step - loss: 0.4939 - custom_accuracy: 0.8304 - val_loss: 0.4734 - val_custom_accuracy: 0.8750 Epoch 22/25 7/7 [==============================] - 1s 138ms/step - loss: 0.4942 - custom_accuracy: 0.8750 - val_loss: 0.4725 - val_custom_accuracy: 0.8750 Epoch 23/25 7/7 [==============================] - 1s 140ms/step - loss: 0.4982 - custom_accuracy: 0.9107 - val_loss: 0.4695 - val_custom_accuracy: 0.8958 Epoch 24/25 7/7 [==============================] - 1s 135ms/step - loss: 0.4936 - custom_accuracy: 0.8661 - val_loss: 0.4731 - val_custom_accuracy: 0.8750 Epoch 25/25 7/7 [==============================] - 1s 136ms/step - loss: 0.4866 - custom_accuracy: 0.8571 - val_loss: 0.4631 - val_custom_accuracy: 0.8958
plt.plot(history.history['loss'][1:], label='Training')
plt.plot(history.history['val_loss'][1:], label='Validation')
plt.title('Training a Quantum CNN to Detect Excited Cluster States')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

2. Modele hybrydowe
Nie musisz przechodzić od ośmiu kubitów do jednego kubitu za pomocą splotu kwantowego — można było wykonać jedną lub dwie rundy splotu kwantowego i wprowadzić wyniki do klasycznej sieci neuronowej. W tej części omówiono kwantowo-klasyczne modele hybrydowe.
2.1 Model hybrydowy z pojedynczym filtrem kwantowym
Zastosuj jedną warstwę splotu kwantowego, odczytując \(\langle \hat{Z}_n \rangle\) na wszystkich bitach, a następnie gęsto połączoną sieć neuronową.

2.1.1 Definicja modelu
# 1-local operators to read out
readouts = [cirq.Z(bit) for bit in cluster_state_bits[4:]]
def multi_readout_model_circuit(qubits):
"""Make a model circuit with less quantum pool and conv operations."""
model_circuit = cirq.Circuit()
symbols = sympy.symbols('qconv0:21')
model_circuit += quantum_conv_circuit(qubits, symbols[0:15])
model_circuit += quantum_pool_circuit(qubits[:4], qubits[4:],
symbols[15:21])
return model_circuit
# Build a model enacting the logic in 2.1 of this notebook.
excitation_input_dual = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
cluster_state_dual = tfq.layers.AddCircuit()(
excitation_input_dual, prepend=cluster_state_circuit(cluster_state_bits))
quantum_model_dual = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_dual)
d1_dual = tf.keras.layers.Dense(8)(quantum_model_dual)
d2_dual = tf.keras.layers.Dense(1)(d1_dual)
hybrid_model = tf.keras.Model(inputs=[excitation_input_dual], outputs=[d2_dual])
# Display the model architecture
tf.keras.utils.plot_model(hybrid_model,
show_shapes=True,
show_layer_names=False,
dpi=70)
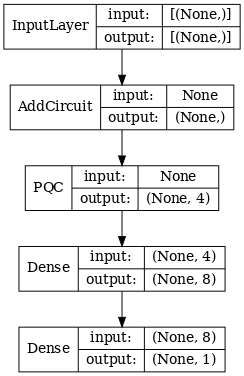
2.1.2 Trenuj modelkę
hybrid_model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.losses.mse,
metrics=[custom_accuracy])
hybrid_history = hybrid_model.fit(x=train_excitations,
y=train_labels,
batch_size=16,
epochs=25,
verbose=1,
validation_data=(test_excitations,
test_labels))
Epoch 1/25 7/7 [==============================] - 1s 113ms/step - loss: 0.9848 - custom_accuracy: 0.5179 - val_loss: 0.9635 - val_custom_accuracy: 0.5417 Epoch 2/25 7/7 [==============================] - 1s 86ms/step - loss: 0.8095 - custom_accuracy: 0.6339 - val_loss: 0.6800 - val_custom_accuracy: 0.7083 Epoch 3/25 7/7 [==============================] - 1s 85ms/step - loss: 0.4045 - custom_accuracy: 0.9375 - val_loss: 0.3342 - val_custom_accuracy: 0.8750 Epoch 4/25 7/7 [==============================] - 1s 86ms/step - loss: 0.2308 - custom_accuracy: 0.9643 - val_loss: 0.2027 - val_custom_accuracy: 0.9792 Epoch 5/25 7/7 [==============================] - 1s 84ms/step - loss: 0.2232 - custom_accuracy: 0.9554 - val_loss: 0.1761 - val_custom_accuracy: 1.0000 Epoch 6/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1760 - custom_accuracy: 0.9821 - val_loss: 0.2541 - val_custom_accuracy: 0.9167 Epoch 7/25 7/7 [==============================] - 1s 85ms/step - loss: 0.1919 - custom_accuracy: 0.9643 - val_loss: 0.1967 - val_custom_accuracy: 0.9792 Epoch 8/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1892 - custom_accuracy: 0.9554 - val_loss: 0.1870 - val_custom_accuracy: 0.9792 Epoch 9/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1777 - custom_accuracy: 0.9911 - val_loss: 0.2208 - val_custom_accuracy: 0.9583 Epoch 10/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1728 - custom_accuracy: 0.9732 - val_loss: 0.2147 - val_custom_accuracy: 0.9583 Epoch 11/25 7/7 [==============================] - 1s 85ms/step - loss: 0.1704 - custom_accuracy: 0.9732 - val_loss: 0.1810 - val_custom_accuracy: 0.9792 Epoch 12/25 7/7 [==============================] - 1s 85ms/step - loss: 0.1739 - custom_accuracy: 0.9732 - val_loss: 0.2038 - val_custom_accuracy: 0.9792 Epoch 13/25 7/7 [==============================] - 1s 81ms/step - loss: 0.1705 - custom_accuracy: 0.9732 - val_loss: 0.1855 - val_custom_accuracy: 0.9792 Epoch 14/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1788 - custom_accuracy: 0.9643 - val_loss: 0.2152 - val_custom_accuracy: 0.9583 Epoch 15/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1760 - custom_accuracy: 0.9732 - val_loss: 0.1994 - val_custom_accuracy: 1.0000 Epoch 16/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1737 - custom_accuracy: 0.9732 - val_loss: 0.2035 - val_custom_accuracy: 0.9792 Epoch 17/25 7/7 [==============================] - 1s 82ms/step - loss: 0.1749 - custom_accuracy: 0.9911 - val_loss: 0.1983 - val_custom_accuracy: 0.9583 Epoch 18/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1875 - custom_accuracy: 0.9732 - val_loss: 0.1916 - val_custom_accuracy: 0.9583 Epoch 19/25 7/7 [==============================] - 1s 82ms/step - loss: 0.1605 - custom_accuracy: 0.9732 - val_loss: 0.1782 - val_custom_accuracy: 0.9792 Epoch 20/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1668 - custom_accuracy: 0.9911 - val_loss: 0.2276 - val_custom_accuracy: 0.9583 Epoch 21/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1700 - custom_accuracy: 0.9911 - val_loss: 0.2080 - val_custom_accuracy: 0.9583 Epoch 22/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1621 - custom_accuracy: 0.9732 - val_loss: 0.1851 - val_custom_accuracy: 0.9375 Epoch 23/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1695 - custom_accuracy: 0.9911 - val_loss: 0.1882 - val_custom_accuracy: 0.9792 Epoch 24/25 7/7 [==============================] - 1s 82ms/step - loss: 0.1583 - custom_accuracy: 0.9911 - val_loss: 0.2017 - val_custom_accuracy: 0.9583 Epoch 25/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1557 - custom_accuracy: 0.9911 - val_loss: 0.1907 - val_custom_accuracy: 0.9792
plt.plot(history.history['val_custom_accuracy'], label='QCNN')
plt.plot(hybrid_history.history['val_custom_accuracy'], label='Hybrid CNN')
plt.title('Quantum vs Hybrid CNN performance')
plt.xlabel('Epochs')
plt.legend()
plt.ylabel('Validation Accuracy')
plt.show()

Jak widać, przy bardzo skromnej pomocy klasycznej, model hybrydowy zwykle zbiega się szybciej niż wersja czysto kwantowa.
2.2 Splot hybrydowy z wieloma filtrami kwantowymi
Wypróbujmy teraz architekturę wykorzystującą wiele splotów kwantowych i klasyczną sieć neuronową do ich połączenia.

2.2.1 Definicja modelu
excitation_input_multi = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
cluster_state_multi = tfq.layers.AddCircuit()(
excitation_input_multi, prepend=cluster_state_circuit(cluster_state_bits))
# apply 3 different filters and measure expectation values
quantum_model_multi1 = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_multi)
quantum_model_multi2 = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_multi)
quantum_model_multi3 = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_multi)
# concatenate outputs and feed into a small classical NN
concat_out = tf.keras.layers.concatenate(
[quantum_model_multi1, quantum_model_multi2, quantum_model_multi3])
dense_1 = tf.keras.layers.Dense(8)(concat_out)
dense_2 = tf.keras.layers.Dense(1)(dense_1)
multi_qconv_model = tf.keras.Model(inputs=[excitation_input_multi],
outputs=[dense_2])
# Display the model architecture
tf.keras.utils.plot_model(multi_qconv_model,
show_shapes=True,
show_layer_names=True,
dpi=70)
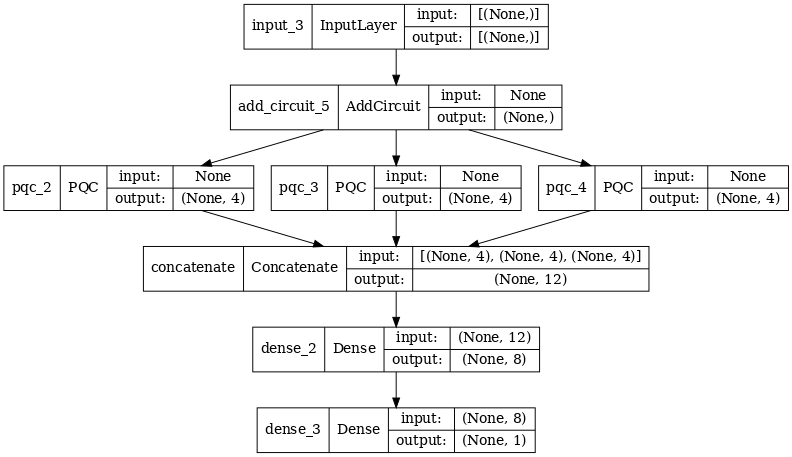
2.2.2 Trenuj modelkę
multi_qconv_model.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.losses.mse,
metrics=[custom_accuracy])
multi_qconv_history = multi_qconv_model.fit(x=train_excitations,
y=train_labels,
batch_size=16,
epochs=25,
verbose=1,
validation_data=(test_excitations,
test_labels))
Epoch 1/25 7/7 [==============================] - 2s 143ms/step - loss: 0.9425 - custom_accuracy: 0.6429 - val_loss: 0.8120 - val_custom_accuracy: 0.7083 Epoch 2/25 7/7 [==============================] - 1s 109ms/step - loss: 0.5778 - custom_accuracy: 0.7946 - val_loss: 0.5920 - val_custom_accuracy: 0.7500 Epoch 3/25 7/7 [==============================] - 1s 103ms/step - loss: 0.4954 - custom_accuracy: 0.9018 - val_loss: 0.4568 - val_custom_accuracy: 0.7708 Epoch 4/25 7/7 [==============================] - 1s 95ms/step - loss: 0.2855 - custom_accuracy: 0.9196 - val_loss: 0.2792 - val_custom_accuracy: 0.9375 Epoch 5/25 7/7 [==============================] - 1s 93ms/step - loss: 0.1902 - custom_accuracy: 0.9821 - val_loss: 0.2212 - val_custom_accuracy: 0.9375 Epoch 6/25 7/7 [==============================] - 1s 94ms/step - loss: 0.1685 - custom_accuracy: 0.9821 - val_loss: 0.2341 - val_custom_accuracy: 0.9583 Epoch 7/25 7/7 [==============================] - 1s 104ms/step - loss: 0.1671 - custom_accuracy: 0.9911 - val_loss: 0.2062 - val_custom_accuracy: 0.9792 Epoch 8/25 7/7 [==============================] - 1s 97ms/step - loss: 0.1511 - custom_accuracy: 0.9821 - val_loss: 0.2096 - val_custom_accuracy: 0.9792 Epoch 9/25 7/7 [==============================] - 1s 96ms/step - loss: 0.1432 - custom_accuracy: 0.9911 - val_loss: 0.2330 - val_custom_accuracy: 0.9375 Epoch 10/25 7/7 [==============================] - 1s 92ms/step - loss: 0.1668 - custom_accuracy: 0.9821 - val_loss: 0.2344 - val_custom_accuracy: 0.9583 Epoch 11/25 7/7 [==============================] - 1s 106ms/step - loss: 0.1893 - custom_accuracy: 0.9732 - val_loss: 0.2148 - val_custom_accuracy: 0.9583 Epoch 12/25 7/7 [==============================] - 1s 104ms/step - loss: 0.1857 - custom_accuracy: 0.9732 - val_loss: 0.2739 - val_custom_accuracy: 0.9583 Epoch 13/25 7/7 [==============================] - 1s 106ms/step - loss: 0.1748 - custom_accuracy: 0.9732 - val_loss: 0.2366 - val_custom_accuracy: 0.9583 Epoch 14/25 7/7 [==============================] - 1s 103ms/step - loss: 0.1515 - custom_accuracy: 0.9821 - val_loss: 0.2012 - val_custom_accuracy: 0.9583 Epoch 15/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1552 - custom_accuracy: 0.9911 - val_loss: 0.2404 - val_custom_accuracy: 0.9375 Epoch 16/25 7/7 [==============================] - 1s 97ms/step - loss: 0.1572 - custom_accuracy: 0.9911 - val_loss: 0.2779 - val_custom_accuracy: 0.9375 Epoch 17/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1546 - custom_accuracy: 0.9821 - val_loss: 0.2104 - val_custom_accuracy: 0.9583 Epoch 18/25 7/7 [==============================] - 1s 102ms/step - loss: 0.1418 - custom_accuracy: 0.9911 - val_loss: 0.2647 - val_custom_accuracy: 0.9583 Epoch 19/25 7/7 [==============================] - 1s 98ms/step - loss: 0.1590 - custom_accuracy: 0.9732 - val_loss: 0.2154 - val_custom_accuracy: 0.9583 Epoch 20/25 7/7 [==============================] - 1s 104ms/step - loss: 0.1363 - custom_accuracy: 1.0000 - val_loss: 0.2470 - val_custom_accuracy: 0.9375 Epoch 21/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1442 - custom_accuracy: 0.9821 - val_loss: 0.2383 - val_custom_accuracy: 0.9375 Epoch 22/25 7/7 [==============================] - 1s 99ms/step - loss: 0.1415 - custom_accuracy: 0.9911 - val_loss: 0.2324 - val_custom_accuracy: 0.9583 Epoch 23/25 7/7 [==============================] - 1s 97ms/step - loss: 0.1424 - custom_accuracy: 0.9821 - val_loss: 0.2188 - val_custom_accuracy: 0.9583 Epoch 24/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1417 - custom_accuracy: 0.9821 - val_loss: 0.2340 - val_custom_accuracy: 0.9375 Epoch 25/25 7/7 [==============================] - 1s 103ms/step - loss: 0.1471 - custom_accuracy: 0.9732 - val_loss: 0.2252 - val_custom_accuracy: 0.9583
plt.plot(history.history['val_custom_accuracy'][:25], label='QCNN')
plt.plot(hybrid_history.history['val_custom_accuracy'][:25], label='Hybrid CNN')
plt.plot(multi_qconv_history.history['val_custom_accuracy'][:25],
label='Hybrid CNN \n Multiple Quantum Filters')
plt.title('Quantum vs Hybrid CNN performance')
plt.xlabel('Epochs')
plt.legend()
plt.ylabel('Validation Accuracy')
plt.show()

