 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Bu öğretici, aynı zamanda çevirisel olarak değişmez olan klasik bir evrişimsel sinir ağına önerilen bir kuantum analogu olan basitleştirilmiş bir Kuantum Evrişimli Sinir Ağı (QCNN) uygular.
Bu örnek, bir kuantum sensörü veya bir cihazdan karmaşık bir simülasyon gibi bir kuantum veri kaynağının belirli özelliklerinin nasıl tespit edileceğini gösterir. Kuantum veri kaynağı, bir uyarıya sahip olabilen veya olmayabilen bir küme durumudur - QCNN'nin algılamayı öğreneceği şey (Kağıtta kullanılan veri kümesi SPT faz sınıflandırmasıydı).
Kurmak
pip install tensorflow==2.7.0
TensorFlow Quantum'u yükleyin:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Şimdi TensorFlow ve modül bağımlılıklarını içe aktarın:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:43:45.380301: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Bir QCNN oluşturun
1.1 Devreleri TensorFlow grafiğinde birleştirme
TensorFlow Quantum (TFQ), grafik içi devre yapımı için tasarlanmış katman sınıfları sağlar. Bir örnek, tf.keras.Layer öğesinden miras alan tfq.layers.AddCircuit tf.keras.Layer . Bu katman, aşağıdaki şekilde gösterildiği gibi, devrelerin giriş partisinin başına veya sonuna eklenebilir.

Aşağıdaki kod parçası bu katmanı kullanır:
qubit = cirq.GridQubit(0, 0)
# Define some circuits.
circuit1 = cirq.Circuit(cirq.X(qubit))
circuit2 = cirq.Circuit(cirq.H(qubit))
# Convert to a tensor.
input_circuit_tensor = tfq.convert_to_tensor([circuit1, circuit2])
# Define a circuit that we want to append
y_circuit = cirq.Circuit(cirq.Y(qubit))
# Instantiate our layer
y_appender = tfq.layers.AddCircuit()
# Run our circuit tensor through the layer and save the output.
output_circuit_tensor = y_appender(input_circuit_tensor, append=y_circuit)
Giriş tensörünü inceleyin:
print(tfq.from_tensor(input_circuit_tensor))
[cirq.Circuit([
cirq.Moment(
cirq.X(cirq.GridQubit(0, 0)),
),
])
cirq.Circuit([
cirq.Moment(
cirq.H(cirq.GridQubit(0, 0)),
),
]) ]
Ve çıkış tensörünü inceleyin:
print(tfq.from_tensor(output_circuit_tensor))
[cirq.Circuit([
cirq.Moment(
cirq.X(cirq.GridQubit(0, 0)),
),
cirq.Moment(
cirq.Y(cirq.GridQubit(0, 0)),
),
])
cirq.Circuit([
cirq.Moment(
cirq.H(cirq.GridQubit(0, 0)),
),
cirq.Moment(
cirq.Y(cirq.GridQubit(0, 0)),
),
]) ]
Aşağıdaki örnekleri tfq.layers.AddCircuit kullanmadan çalıştırmak mümkün olsa da, karmaşık işlevlerin TensorFlow hesaplama grafiklerine nasıl yerleştirilebileceğini anlamak için iyi bir fırsat.
1.2 Soruna genel bakış
Bir küme durumu hazırlayacak ve "heyecanlı" olup olmadığını saptamak için bir kuantum sınıflandırıcı eğiteceksiniz. Küme durumu oldukça karışıktır ancak klasik bir bilgisayar için mutlaka zor değildir. Anlaşılır olması açısından bu, makalede kullanılandan daha basit bir veri kümesidir.
Bu sınıflandırma görevi için derin bir MERA benzeri QCNN mimarisi uygulayacaksınız, çünkü:
- QCNN gibi, bir halkadaki küme durumu da öteleme açısından değişmezdir.
- Küme durumu oldukça karışık.
Bu mimari, tek bir kübiti okuyarak sınıflandırmayı elde ederek dolaşıklığı azaltmada etkili olmalıdır.

"Uyarılmış" bir küme durumu, herhangi bir kübitine uygulanan bir cirq.rx kapısına sahip bir küme durumu olarak tanımlanır. Qconv ve QPool bu öğreticide daha sonra tartışılacaktır.
1.3 TensorFlow için yapı taşları

Bu sorunu TensorFlow Quantum ile çözmenin bir yolu aşağıdakileri uygulamaktır:
- Modelin girdisi bir devre tensörüdür - ya boş bir devre ya da belirli bir kübit üzerindeki bir uyarımı gösteren bir X kapısı.
- Modelin kuantum bileşenlerinin geri kalanı
tfq.layers.AddCircuitkatmanlarıyla oluşturulmuştur. - Çıkarım için bir
tfq.layers.PQCkatmanı kullanılır. Bu, \(\langle \hat{Z} \rangle\) okur ve uyarılmış bir durum için 1 veya uyarılmamış bir durum için -1 etiketiyle karşılaştırır.
1.4 Veri
Modelinizi oluşturmadan önce verilerinizi oluşturabilirsiniz. Bu durumda küme durumuna yönelik uyarılar olacaktır (Orijinal makale daha karmaşık bir veri kümesi kullanır). cirq.rx kapıları ile temsil edilir. Yeterince büyük bir dönüş bir uyarı olarak kabul edilir ve 1 olarak etiketlenir ve yeterince büyük olmayan bir dönüş -1 olarak etiketlenir ve bir uyarı olarak kabul edilmez.
def generate_data(qubits):
"""Generate training and testing data."""
n_rounds = 20 # Produces n_rounds * n_qubits datapoints.
excitations = []
labels = []
for n in range(n_rounds):
for bit in qubits:
rng = np.random.uniform(-np.pi, np.pi)
excitations.append(cirq.Circuit(cirq.rx(rng)(bit)))
labels.append(1 if (-np.pi / 2) <= rng <= (np.pi / 2) else -1)
split_ind = int(len(excitations) * 0.7)
train_excitations = excitations[:split_ind]
test_excitations = excitations[split_ind:]
train_labels = labels[:split_ind]
test_labels = labels[split_ind:]
return tfq.convert_to_tensor(train_excitations), np.array(train_labels), \
tfq.convert_to_tensor(test_excitations), np.array(test_labels)
Tıpkı normal makine öğreniminde olduğu gibi, modeli kıyaslamak için kullanmak üzere bir eğitim ve test seti oluşturduğunuzu görebilirsiniz. Aşağıdakilerle bazı veri noktalarına hızlıca bakabilirsiniz:
sample_points, sample_labels, _, __ = generate_data(cirq.GridQubit.rect(1, 4))
print('Input:', tfq.from_tensor(sample_points)[0], 'Output:', sample_labels[0])
print('Input:', tfq.from_tensor(sample_points)[1], 'Output:', sample_labels[1])
Input: (0, 0): ───X^0.449─── Output: 1 Input: (0, 1): ───X^-0.74─── Output: -1
1.5 Katmanları tanımlayın
Şimdi yukarıdaki şekilde gösterilen katmanları TensorFlow'da tanımlayın.
1.5.1 Küme durumu
İlk adım, kuantum devrelerini programlamak için Google tarafından sağlanan bir çerçeve olan Cirq'i kullanarak küme durumunu tanımlamaktır. Bu, modelin statik bir parçası olduğundan, onu tfq.layers.AddCircuit işlevini kullanarak gömün.
def cluster_state_circuit(bits):
"""Return a cluster state on the qubits in `bits`."""
circuit = cirq.Circuit()
circuit.append(cirq.H.on_each(bits))
for this_bit, next_bit in zip(bits, bits[1:] + [bits[0]]):
circuit.append(cirq.CZ(this_bit, next_bit))
return circuit
cirq.GridQubit s dikdörtgeni için bir küme durumu devresi görüntüleyin:
SVGCircuit(cluster_state_circuit(cirq.GridQubit.rect(1, 4)))
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
1.5.2 QCNN katmanları
Cong ve Lukin QCNN kağıdını kullanarak modeli oluşturan katmanları tanımlayın. Birkaç önkoşul vardır:
- Tucci makalesinden bir ve iki kübitlik parametreli üniter matrisler.
- Genel bir parametreli iki kübit havuzlama işlemi.
def one_qubit_unitary(bit, symbols):
"""Make a Cirq circuit enacting a rotation of the bloch sphere about the X,
Y and Z axis, that depends on the values in `symbols`.
"""
return cirq.Circuit(
cirq.X(bit)**symbols[0],
cirq.Y(bit)**symbols[1],
cirq.Z(bit)**symbols[2])
def two_qubit_unitary(bits, symbols):
"""Make a Cirq circuit that creates an arbitrary two qubit unitary."""
circuit = cirq.Circuit()
circuit += one_qubit_unitary(bits[0], symbols[0:3])
circuit += one_qubit_unitary(bits[1], symbols[3:6])
circuit += [cirq.ZZ(*bits)**symbols[6]]
circuit += [cirq.YY(*bits)**symbols[7]]
circuit += [cirq.XX(*bits)**symbols[8]]
circuit += one_qubit_unitary(bits[0], symbols[9:12])
circuit += one_qubit_unitary(bits[1], symbols[12:])
return circuit
def two_qubit_pool(source_qubit, sink_qubit, symbols):
"""Make a Cirq circuit to do a parameterized 'pooling' operation, which
attempts to reduce entanglement down from two qubits to just one."""
pool_circuit = cirq.Circuit()
sink_basis_selector = one_qubit_unitary(sink_qubit, symbols[0:3])
source_basis_selector = one_qubit_unitary(source_qubit, symbols[3:6])
pool_circuit.append(sink_basis_selector)
pool_circuit.append(source_basis_selector)
pool_circuit.append(cirq.CNOT(control=source_qubit, target=sink_qubit))
pool_circuit.append(sink_basis_selector**-1)
return pool_circuit
Ne yarattığınızı görmek için tek kübitlik üniter devreyi yazdırın:
SVGCircuit(one_qubit_unitary(cirq.GridQubit(0, 0), sympy.symbols('x0:3')))
Ve iki kübitlik üniter devre:
SVGCircuit(two_qubit_unitary(cirq.GridQubit.rect(1, 2), sympy.symbols('x0:15')))
Ve iki kübit havuzlama devresi:
SVGCircuit(two_qubit_pool(*cirq.GridQubit.rect(1, 2), sympy.symbols('x0:6')))
1.5.2.1 Kuantum evrişim
Cong ve Lukin makalesinde olduğu gibi, 1B kuantum evrişimini, iki kübitlik parametreli bir ünitenin, bir adımlık her bitişik kübit çiftine uygulanması olarak tanımlayın.
def quantum_conv_circuit(bits, symbols):
"""Quantum Convolution Layer following the above diagram.
Return a Cirq circuit with the cascade of `two_qubit_unitary` applied
to all pairs of qubits in `bits` as in the diagram above.
"""
circuit = cirq.Circuit()
for first, second in zip(bits[0::2], bits[1::2]):
circuit += two_qubit_unitary([first, second], symbols)
for first, second in zip(bits[1::2], bits[2::2] + [bits[0]]):
circuit += two_qubit_unitary([first, second], symbols)
return circuit
(çok yatay) devreyi görüntüleyin:
SVGCircuit(
quantum_conv_circuit(cirq.GridQubit.rect(1, 8), sympy.symbols('x0:15')))
1.5.2.2 Kuantum havuzu
Bir kuantum havuzlama katmanı, yukarıda tanımlanan iki kübitlik havuzu kullanarak l10n \(N\) yer tutucu2 kübitlerden \(\frac{N}{2}\) tutucu3 kübitlere havuzlar.
def quantum_pool_circuit(source_bits, sink_bits, symbols):
"""A layer that specifies a quantum pooling operation.
A Quantum pool tries to learn to pool the relevant information from two
qubits onto 1.
"""
circuit = cirq.Circuit()
for source, sink in zip(source_bits, sink_bits):
circuit += two_qubit_pool(source, sink, symbols)
return circuit
Bir havuzlama bileşen devresini inceleyin:
test_bits = cirq.GridQubit.rect(1, 8)
SVGCircuit(
quantum_pool_circuit(test_bits[:4], test_bits[4:], sympy.symbols('x0:6')))
1.6 Model tanımı
Şimdi tamamen kuantum bir CNN oluşturmak için tanımlanmış katmanları kullanın. Sekiz kübitle başlayın, bire indirgeyin, ardından \(\langle \hat{Z} \rangle\)ölçün.
def create_model_circuit(qubits):
"""Create sequence of alternating convolution and pooling operators
which gradually shrink over time."""
model_circuit = cirq.Circuit()
symbols = sympy.symbols('qconv0:63')
# Cirq uses sympy.Symbols to map learnable variables. TensorFlow Quantum
# scans incoming circuits and replaces these with TensorFlow variables.
model_circuit += quantum_conv_circuit(qubits, symbols[0:15])
model_circuit += quantum_pool_circuit(qubits[:4], qubits[4:],
symbols[15:21])
model_circuit += quantum_conv_circuit(qubits[4:], symbols[21:36])
model_circuit += quantum_pool_circuit(qubits[4:6], qubits[6:],
symbols[36:42])
model_circuit += quantum_conv_circuit(qubits[6:], symbols[42:57])
model_circuit += quantum_pool_circuit([qubits[6]], [qubits[7]],
symbols[57:63])
return model_circuit
# Create our qubits and readout operators in Cirq.
cluster_state_bits = cirq.GridQubit.rect(1, 8)
readout_operators = cirq.Z(cluster_state_bits[-1])
# Build a sequential model enacting the logic in 1.3 of this notebook.
# Here you are making the static cluster state prep as a part of the AddCircuit and the
# "quantum datapoints" are coming in the form of excitation
excitation_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
cluster_state = tfq.layers.AddCircuit()(
excitation_input, prepend=cluster_state_circuit(cluster_state_bits))
quantum_model = tfq.layers.PQC(create_model_circuit(cluster_state_bits),
readout_operators)(cluster_state)
qcnn_model = tf.keras.Model(inputs=[excitation_input], outputs=[quantum_model])
# Show the keras plot of the model
tf.keras.utils.plot_model(qcnn_model,
show_shapes=True,
show_layer_names=False,
dpi=70)

1.7 Modeli eğitin
Bu örneği basitleştirmek için modeli tam parti üzerinde eğitin.
# Generate some training data.
train_excitations, train_labels, test_excitations, test_labels = generate_data(
cluster_state_bits)
# Custom accuracy metric.
@tf.function
def custom_accuracy(y_true, y_pred):
y_true = tf.squeeze(y_true)
y_pred = tf.map_fn(lambda x: 1.0 if x >= 0 else -1.0, y_pred)
return tf.keras.backend.mean(tf.keras.backend.equal(y_true, y_pred))
qcnn_model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.losses.mse,
metrics=[custom_accuracy])
history = qcnn_model.fit(x=train_excitations,
y=train_labels,
batch_size=16,
epochs=25,
verbose=1,
validation_data=(test_excitations, test_labels))
Epoch 1/25 7/7 [==============================] - 2s 176ms/step - loss: 0.8961 - custom_accuracy: 0.7143 - val_loss: 0.8012 - val_custom_accuracy: 0.7500 Epoch 2/25 7/7 [==============================] - 1s 140ms/step - loss: 0.7736 - custom_accuracy: 0.7946 - val_loss: 0.7355 - val_custom_accuracy: 0.8542 Epoch 3/25 7/7 [==============================] - 1s 138ms/step - loss: 0.7319 - custom_accuracy: 0.8393 - val_loss: 0.7045 - val_custom_accuracy: 0.8125 Epoch 4/25 7/7 [==============================] - 1s 137ms/step - loss: 0.6976 - custom_accuracy: 0.8482 - val_loss: 0.6829 - val_custom_accuracy: 0.8333 Epoch 5/25 7/7 [==============================] - 1s 143ms/step - loss: 0.6696 - custom_accuracy: 0.8750 - val_loss: 0.6749 - val_custom_accuracy: 0.7917 Epoch 6/25 7/7 [==============================] - 1s 137ms/step - loss: 0.6631 - custom_accuracy: 0.8750 - val_loss: 0.6718 - val_custom_accuracy: 0.7917 Epoch 7/25 7/7 [==============================] - 1s 135ms/step - loss: 0.6536 - custom_accuracy: 0.8929 - val_loss: 0.6638 - val_custom_accuracy: 0.8750 Epoch 8/25 7/7 [==============================] - 1s 141ms/step - loss: 0.6376 - custom_accuracy: 0.8750 - val_loss: 0.6311 - val_custom_accuracy: 0.8542 Epoch 9/25 7/7 [==============================] - 1s 137ms/step - loss: 0.6208 - custom_accuracy: 0.8750 - val_loss: 0.5995 - val_custom_accuracy: 0.8542 Epoch 10/25 7/7 [==============================] - 1s 134ms/step - loss: 0.5887 - custom_accuracy: 0.8661 - val_loss: 0.5655 - val_custom_accuracy: 0.8333 Epoch 11/25 7/7 [==============================] - 1s 144ms/step - loss: 0.5796 - custom_accuracy: 0.8482 - val_loss: 0.5681 - val_custom_accuracy: 0.8333 Epoch 12/25 7/7 [==============================] - 1s 143ms/step - loss: 0.5630 - custom_accuracy: 0.7946 - val_loss: 0.5179 - val_custom_accuracy: 0.8333 Epoch 13/25 7/7 [==============================] - 1s 137ms/step - loss: 0.5405 - custom_accuracy: 0.8304 - val_loss: 0.5003 - val_custom_accuracy: 0.8333 Epoch 14/25 7/7 [==============================] - 1s 138ms/step - loss: 0.5259 - custom_accuracy: 0.8036 - val_loss: 0.4787 - val_custom_accuracy: 0.8333 Epoch 15/25 7/7 [==============================] - 1s 137ms/step - loss: 0.5077 - custom_accuracy: 0.8482 - val_loss: 0.4741 - val_custom_accuracy: 0.8125 Epoch 16/25 7/7 [==============================] - 1s 136ms/step - loss: 0.5082 - custom_accuracy: 0.8214 - val_loss: 0.4739 - val_custom_accuracy: 0.8125 Epoch 17/25 7/7 [==============================] - 1s 137ms/step - loss: 0.5138 - custom_accuracy: 0.8214 - val_loss: 0.4859 - val_custom_accuracy: 0.8750 Epoch 18/25 7/7 [==============================] - 1s 133ms/step - loss: 0.5073 - custom_accuracy: 0.8304 - val_loss: 0.4879 - val_custom_accuracy: 0.8333 Epoch 19/25 7/7 [==============================] - 1s 138ms/step - loss: 0.5084 - custom_accuracy: 0.8304 - val_loss: 0.4745 - val_custom_accuracy: 0.8542 Epoch 20/25 7/7 [==============================] - 1s 139ms/step - loss: 0.5057 - custom_accuracy: 0.8571 - val_loss: 0.4702 - val_custom_accuracy: 0.8333 Epoch 21/25 7/7 [==============================] - 1s 135ms/step - loss: 0.4939 - custom_accuracy: 0.8304 - val_loss: 0.4734 - val_custom_accuracy: 0.8750 Epoch 22/25 7/7 [==============================] - 1s 138ms/step - loss: 0.4942 - custom_accuracy: 0.8750 - val_loss: 0.4725 - val_custom_accuracy: 0.8750 Epoch 23/25 7/7 [==============================] - 1s 140ms/step - loss: 0.4982 - custom_accuracy: 0.9107 - val_loss: 0.4695 - val_custom_accuracy: 0.8958 Epoch 24/25 7/7 [==============================] - 1s 135ms/step - loss: 0.4936 - custom_accuracy: 0.8661 - val_loss: 0.4731 - val_custom_accuracy: 0.8750 Epoch 25/25 7/7 [==============================] - 1s 136ms/step - loss: 0.4866 - custom_accuracy: 0.8571 - val_loss: 0.4631 - val_custom_accuracy: 0.8958-yer tutucu33 l10n-yer
plt.plot(history.history['loss'][1:], label='Training')
plt.plot(history.history['val_loss'][1:], label='Validation')
plt.title('Training a Quantum CNN to Detect Excited Cluster States')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

2. Hibrit modeller
Kuantum evrişimi kullanarak sekiz kübitten bir kübite gitmek zorunda değilsiniz - bir veya iki tur kuantum evrişimi yapabilir ve sonuçları klasik bir sinir ağına besleyebilirdiniz. Bu bölüm kuantum-klasik hibrit modelleri incelemektedir.
2.1 Tek bir kuantum filtreli hibrit model
Tüm bitlerde \(\langle \hat{Z}_n \rangle\) okuyarak bir kuantum evrişim katmanı uygulayın ve ardından yoğun bağlantılı bir sinir ağı uygulayın.

2.1.1 Model tanımı
# 1-local operators to read out
readouts = [cirq.Z(bit) for bit in cluster_state_bits[4:]]
def multi_readout_model_circuit(qubits):
"""Make a model circuit with less quantum pool and conv operations."""
model_circuit = cirq.Circuit()
symbols = sympy.symbols('qconv0:21')
model_circuit += quantum_conv_circuit(qubits, symbols[0:15])
model_circuit += quantum_pool_circuit(qubits[:4], qubits[4:],
symbols[15:21])
return model_circuit
# Build a model enacting the logic in 2.1 of this notebook.
excitation_input_dual = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
cluster_state_dual = tfq.layers.AddCircuit()(
excitation_input_dual, prepend=cluster_state_circuit(cluster_state_bits))
quantum_model_dual = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_dual)
d1_dual = tf.keras.layers.Dense(8)(quantum_model_dual)
d2_dual = tf.keras.layers.Dense(1)(d1_dual)
hybrid_model = tf.keras.Model(inputs=[excitation_input_dual], outputs=[d2_dual])
# Display the model architecture
tf.keras.utils.plot_model(hybrid_model,
show_shapes=True,
show_layer_names=False,
dpi=70)
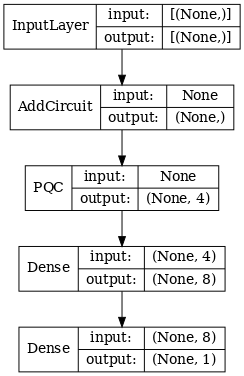
2.1.2 Modeli eğitin
hybrid_model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.losses.mse,
metrics=[custom_accuracy])
hybrid_history = hybrid_model.fit(x=train_excitations,
y=train_labels,
batch_size=16,
epochs=25,
verbose=1,
validation_data=(test_excitations,
test_labels))
Epoch 1/25 7/7 [==============================] - 1s 113ms/step - loss: 0.9848 - custom_accuracy: 0.5179 - val_loss: 0.9635 - val_custom_accuracy: 0.5417 Epoch 2/25 7/7 [==============================] - 1s 86ms/step - loss: 0.8095 - custom_accuracy: 0.6339 - val_loss: 0.6800 - val_custom_accuracy: 0.7083 Epoch 3/25 7/7 [==============================] - 1s 85ms/step - loss: 0.4045 - custom_accuracy: 0.9375 - val_loss: 0.3342 - val_custom_accuracy: 0.8750 Epoch 4/25 7/7 [==============================] - 1s 86ms/step - loss: 0.2308 - custom_accuracy: 0.9643 - val_loss: 0.2027 - val_custom_accuracy: 0.9792 Epoch 5/25 7/7 [==============================] - 1s 84ms/step - loss: 0.2232 - custom_accuracy: 0.9554 - val_loss: 0.1761 - val_custom_accuracy: 1.0000 Epoch 6/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1760 - custom_accuracy: 0.9821 - val_loss: 0.2541 - val_custom_accuracy: 0.9167 Epoch 7/25 7/7 [==============================] - 1s 85ms/step - loss: 0.1919 - custom_accuracy: 0.9643 - val_loss: 0.1967 - val_custom_accuracy: 0.9792 Epoch 8/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1892 - custom_accuracy: 0.9554 - val_loss: 0.1870 - val_custom_accuracy: 0.9792 Epoch 9/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1777 - custom_accuracy: 0.9911 - val_loss: 0.2208 - val_custom_accuracy: 0.9583 Epoch 10/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1728 - custom_accuracy: 0.9732 - val_loss: 0.2147 - val_custom_accuracy: 0.9583 Epoch 11/25 7/7 [==============================] - 1s 85ms/step - loss: 0.1704 - custom_accuracy: 0.9732 - val_loss: 0.1810 - val_custom_accuracy: 0.9792 Epoch 12/25 7/7 [==============================] - 1s 85ms/step - loss: 0.1739 - custom_accuracy: 0.9732 - val_loss: 0.2038 - val_custom_accuracy: 0.9792 Epoch 13/25 7/7 [==============================] - 1s 81ms/step - loss: 0.1705 - custom_accuracy: 0.9732 - val_loss: 0.1855 - val_custom_accuracy: 0.9792 Epoch 14/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1788 - custom_accuracy: 0.9643 - val_loss: 0.2152 - val_custom_accuracy: 0.9583 Epoch 15/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1760 - custom_accuracy: 0.9732 - val_loss: 0.1994 - val_custom_accuracy: 1.0000 Epoch 16/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1737 - custom_accuracy: 0.9732 - val_loss: 0.2035 - val_custom_accuracy: 0.9792 Epoch 17/25 7/7 [==============================] - 1s 82ms/step - loss: 0.1749 - custom_accuracy: 0.9911 - val_loss: 0.1983 - val_custom_accuracy: 0.9583 Epoch 18/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1875 - custom_accuracy: 0.9732 - val_loss: 0.1916 - val_custom_accuracy: 0.9583 Epoch 19/25 7/7 [==============================] - 1s 82ms/step - loss: 0.1605 - custom_accuracy: 0.9732 - val_loss: 0.1782 - val_custom_accuracy: 0.9792 Epoch 20/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1668 - custom_accuracy: 0.9911 - val_loss: 0.2276 - val_custom_accuracy: 0.9583 Epoch 21/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1700 - custom_accuracy: 0.9911 - val_loss: 0.2080 - val_custom_accuracy: 0.9583 Epoch 22/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1621 - custom_accuracy: 0.9732 - val_loss: 0.1851 - val_custom_accuracy: 0.9375 Epoch 23/25 7/7 [==============================] - 1s 84ms/step - loss: 0.1695 - custom_accuracy: 0.9911 - val_loss: 0.1882 - val_custom_accuracy: 0.9792 Epoch 24/25 7/7 [==============================] - 1s 82ms/step - loss: 0.1583 - custom_accuracy: 0.9911 - val_loss: 0.2017 - val_custom_accuracy: 0.9583 Epoch 25/25 7/7 [==============================] - 1s 83ms/step - loss: 0.1557 - custom_accuracy: 0.9911 - val_loss: 0.1907 - val_custom_accuracy: 0.9792-yer tutucu37 l10n-yer
plt.plot(history.history['val_custom_accuracy'], label='QCNN')
plt.plot(hybrid_history.history['val_custom_accuracy'], label='Hybrid CNN')
plt.title('Quantum vs Hybrid CNN performance')
plt.xlabel('Epochs')
plt.legend()
plt.ylabel('Validation Accuracy')
plt.show()

Gördüğünüz gibi, çok mütevazı bir klasik yardımla, hibrit model genellikle tamamen kuantum versiyonundan daha hızlı yakınsayacaktır.
2.2 Çoklu kuantum filtreli hibrit evrişim
Şimdi bunları birleştirmek için çoklu kuantum evrişimlerini ve klasik bir sinir ağını kullanan bir mimari deneyelim.

2.2.1 Model tanımı
excitation_input_multi = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
cluster_state_multi = tfq.layers.AddCircuit()(
excitation_input_multi, prepend=cluster_state_circuit(cluster_state_bits))
# apply 3 different filters and measure expectation values
quantum_model_multi1 = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_multi)
quantum_model_multi2 = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_multi)
quantum_model_multi3 = tfq.layers.PQC(
multi_readout_model_circuit(cluster_state_bits),
readouts)(cluster_state_multi)
# concatenate outputs and feed into a small classical NN
concat_out = tf.keras.layers.concatenate(
[quantum_model_multi1, quantum_model_multi2, quantum_model_multi3])
dense_1 = tf.keras.layers.Dense(8)(concat_out)
dense_2 = tf.keras.layers.Dense(1)(dense_1)
multi_qconv_model = tf.keras.Model(inputs=[excitation_input_multi],
outputs=[dense_2])
# Display the model architecture
tf.keras.utils.plot_model(multi_qconv_model,
show_shapes=True,
show_layer_names=True,
dpi=70)
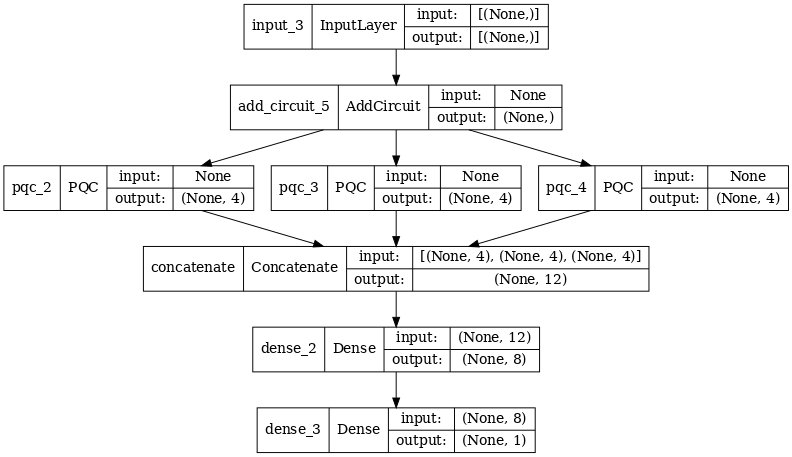
2.2.2 Modeli eğitin
multi_qconv_model.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.losses.mse,
metrics=[custom_accuracy])
multi_qconv_history = multi_qconv_model.fit(x=train_excitations,
y=train_labels,
batch_size=16,
epochs=25,
verbose=1,
validation_data=(test_excitations,
test_labels))
Epoch 1/25 7/7 [==============================] - 2s 143ms/step - loss: 0.9425 - custom_accuracy: 0.6429 - val_loss: 0.8120 - val_custom_accuracy: 0.7083 Epoch 2/25 7/7 [==============================] - 1s 109ms/step - loss: 0.5778 - custom_accuracy: 0.7946 - val_loss: 0.5920 - val_custom_accuracy: 0.7500 Epoch 3/25 7/7 [==============================] - 1s 103ms/step - loss: 0.4954 - custom_accuracy: 0.9018 - val_loss: 0.4568 - val_custom_accuracy: 0.7708 Epoch 4/25 7/7 [==============================] - 1s 95ms/step - loss: 0.2855 - custom_accuracy: 0.9196 - val_loss: 0.2792 - val_custom_accuracy: 0.9375 Epoch 5/25 7/7 [==============================] - 1s 93ms/step - loss: 0.1902 - custom_accuracy: 0.9821 - val_loss: 0.2212 - val_custom_accuracy: 0.9375 Epoch 6/25 7/7 [==============================] - 1s 94ms/step - loss: 0.1685 - custom_accuracy: 0.9821 - val_loss: 0.2341 - val_custom_accuracy: 0.9583 Epoch 7/25 7/7 [==============================] - 1s 104ms/step - loss: 0.1671 - custom_accuracy: 0.9911 - val_loss: 0.2062 - val_custom_accuracy: 0.9792 Epoch 8/25 7/7 [==============================] - 1s 97ms/step - loss: 0.1511 - custom_accuracy: 0.9821 - val_loss: 0.2096 - val_custom_accuracy: 0.9792 Epoch 9/25 7/7 [==============================] - 1s 96ms/step - loss: 0.1432 - custom_accuracy: 0.9911 - val_loss: 0.2330 - val_custom_accuracy: 0.9375 Epoch 10/25 7/7 [==============================] - 1s 92ms/step - loss: 0.1668 - custom_accuracy: 0.9821 - val_loss: 0.2344 - val_custom_accuracy: 0.9583 Epoch 11/25 7/7 [==============================] - 1s 106ms/step - loss: 0.1893 - custom_accuracy: 0.9732 - val_loss: 0.2148 - val_custom_accuracy: 0.9583 Epoch 12/25 7/7 [==============================] - 1s 104ms/step - loss: 0.1857 - custom_accuracy: 0.9732 - val_loss: 0.2739 - val_custom_accuracy: 0.9583 Epoch 13/25 7/7 [==============================] - 1s 106ms/step - loss: 0.1748 - custom_accuracy: 0.9732 - val_loss: 0.2366 - val_custom_accuracy: 0.9583 Epoch 14/25 7/7 [==============================] - 1s 103ms/step - loss: 0.1515 - custom_accuracy: 0.9821 - val_loss: 0.2012 - val_custom_accuracy: 0.9583 Epoch 15/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1552 - custom_accuracy: 0.9911 - val_loss: 0.2404 - val_custom_accuracy: 0.9375 Epoch 16/25 7/7 [==============================] - 1s 97ms/step - loss: 0.1572 - custom_accuracy: 0.9911 - val_loss: 0.2779 - val_custom_accuracy: 0.9375 Epoch 17/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1546 - custom_accuracy: 0.9821 - val_loss: 0.2104 - val_custom_accuracy: 0.9583 Epoch 18/25 7/7 [==============================] - 1s 102ms/step - loss: 0.1418 - custom_accuracy: 0.9911 - val_loss: 0.2647 - val_custom_accuracy: 0.9583 Epoch 19/25 7/7 [==============================] - 1s 98ms/step - loss: 0.1590 - custom_accuracy: 0.9732 - val_loss: 0.2154 - val_custom_accuracy: 0.9583 Epoch 20/25 7/7 [==============================] - 1s 104ms/step - loss: 0.1363 - custom_accuracy: 1.0000 - val_loss: 0.2470 - val_custom_accuracy: 0.9375 Epoch 21/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1442 - custom_accuracy: 0.9821 - val_loss: 0.2383 - val_custom_accuracy: 0.9375 Epoch 22/25 7/7 [==============================] - 1s 99ms/step - loss: 0.1415 - custom_accuracy: 0.9911 - val_loss: 0.2324 - val_custom_accuracy: 0.9583 Epoch 23/25 7/7 [==============================] - 1s 97ms/step - loss: 0.1424 - custom_accuracy: 0.9821 - val_loss: 0.2188 - val_custom_accuracy: 0.9583 Epoch 24/25 7/7 [==============================] - 1s 100ms/step - loss: 0.1417 - custom_accuracy: 0.9821 - val_loss: 0.2340 - val_custom_accuracy: 0.9375 Epoch 25/25 7/7 [==============================] - 1s 103ms/step - loss: 0.1471 - custom_accuracy: 0.9732 - val_loss: 0.2252 - val_custom_accuracy: 0.9583-yer tutucu41 l10n-yer
plt.plot(history.history['val_custom_accuracy'][:25], label='QCNN')
plt.plot(hybrid_history.history['val_custom_accuracy'][:25], label='Hybrid CNN')
plt.plot(multi_qconv_history.history['val_custom_accuracy'][:25],
label='Hybrid CNN \n Multiple Quantum Filters')
plt.title('Quantum vs Hybrid CNN performance')
plt.xlabel('Epochs')
plt.legend()
plt.ylabel('Validation Accuracy')
plt.show()

