Выбор байесовской модели
 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запускаем в Google Colab Запускаем в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
Импорт
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
Задача: обнаружение точек изменения с несколькими точками изменения
Рассмотрим задачу обнаружения точки изменения: события происходят со скоростью, которая меняется со временем, что обусловлено внезапными изменениями (ненаблюдаемого) состояния некоторой системы или процесса, генерирующего данные.
Например, мы можем наблюдать серию таких подсчетов:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
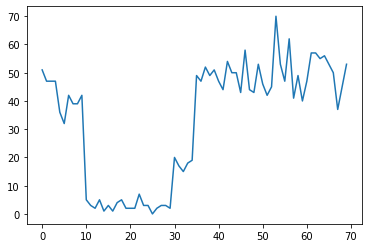
Они могут представлять количество отказов в центре обработки данных, количество посетителей веб-страницы, количество пакетов в сетевой ссылке и т. Д.
Обратите внимание, что не совсем очевидно, сколько различных режимов системы существует, просто глядя на данные. Можете ли вы сказать, где находится каждая из трех точек переключения?
Известное количество состояний
Сначала мы рассмотрим (возможно, нереальный) случай, когда количество ненаблюдаемых состояний известно априори. Здесь мы предполагаем, что знаем, что существует четыре скрытых состояния.
Мы моделировать эту проблему в качестве переключающего (неоднородного) процесса Пуассона: в каждый момент времени, число событий , которые происходят вне Пуассон распределен, и скорость событий определяются ненаблюдаемым состояние системы \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
Латентные состояния дискретны: \(z_t \in \{1, 2, 3, 4\}\), так что \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) является простой вектор , содержащий скорость Пуассона для каждого состояния. Для того, чтобы смоделировать эволюцию состояний с течением времени, мы определим простой переход модели \(p(z_t | z_{t-1})\): допустим , что на каждом шаге мы остаемся в предыдущем состоянии с некоторой вероятностью \(p\), и с вероятностью \(1-p\) мы переходе к различное состояние равномерно случайным образом. Начальное состояние также выбирается равномерно случайным образом, поэтому мы имеем:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
Эти предположения соответствуют скрытой марковской модели с выбросами Пуассона. Мы можем кодировать их в СФП с использованием tfd.HiddenMarkovModel . Сначала мы определяем матрицу перехода и равномерный априор для начального состояния:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
Далее, мы строим tfd.HiddenMarkovModel распределение, используя обучаемые переменную для представления ставки , связанные с каждым состоянием системы. Мы параметризуем ставки в лог-пространстве, чтобы обеспечить их положительное значение.
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
Наконец, мы определяем суммарную плотность журнала в модели, в то числе слабо информативный Логнормальной ранее по ставкам, и запустить оптимизатор для вычисления максимального апостериорный (MAP) прилегания к наблюдаемому количеству данных.
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
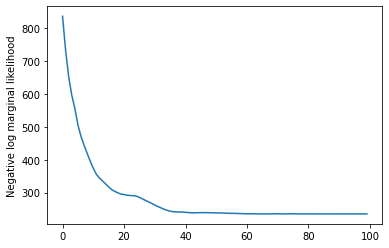
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
Это сработало! Обратите внимание, что латентные состояния в этой модели можно идентифицировать только до перестановки, поэтому восстановленные скорости находятся в другом порядке, и есть небольшой шум, но в целом они довольно хорошо совпадают.
Восстановление траектории состояния
Теперь, когда мы подобрать модель, мы могли бы восстановить состояние , которое модель считает , что система была на каждом временном шаге.
Это задняя задача умозаключения: учитывая наблюдаемые отсчеты \(x_{1:T}\) и параметры модели (ставки) \(\lambda\), мы хотим вывести последовательность дискретных латентных переменных, после заднего распределения \(p(z_{1:T} | x_{1:T}, \lambda)\). В скрытой марковской модели мы можем эффективно вычислять маргиналы и другие свойства этого распределения, используя стандартные алгоритмы передачи сообщений. В частности, posterior_marginals метод эффективного вычисления ( с использованием вперед-назад алгоритм ) предельного распределения вероятностей \(p(Z_t = z_t | x_{1:T})\) над дискретной латентного состояния \(Z_t\) на каждом временном шаге \(t\).
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
Строя апостериорные вероятности, мы восстанавливаем "объяснение" данных модели: в какие моменты времени каждое состояние является активным?
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
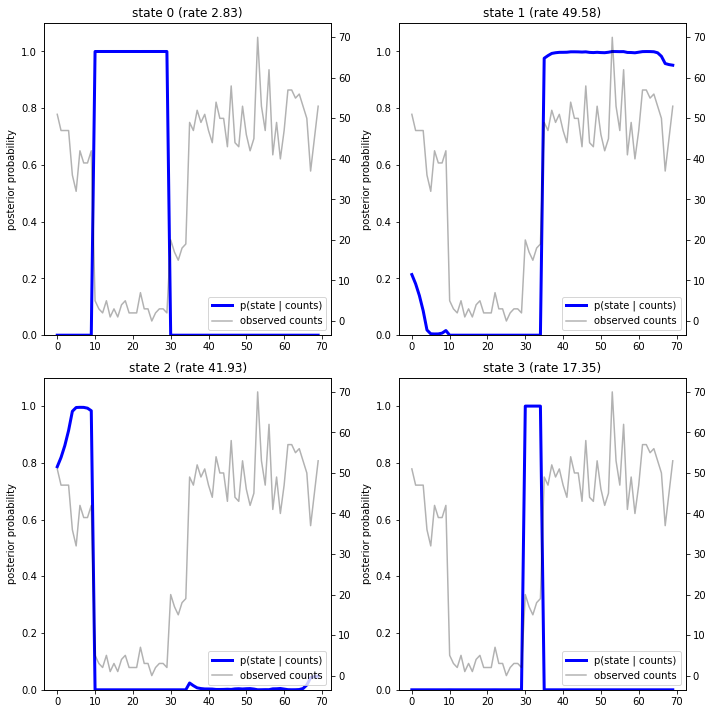
В этом (простом) случае мы видим, что модель обычно довольно надежна: на большинстве временных шагов она присваивает практически всю вероятностную массу одному из четырех состояний. К счастью, объяснения выглядят разумными!
Мы также можем представить себе эту кзади с точки зрения скорости , связанной с наиболее вероятной латентном состоянии на каждом временном шаге, конденсационные вероятностный кзади в одно объяснение:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
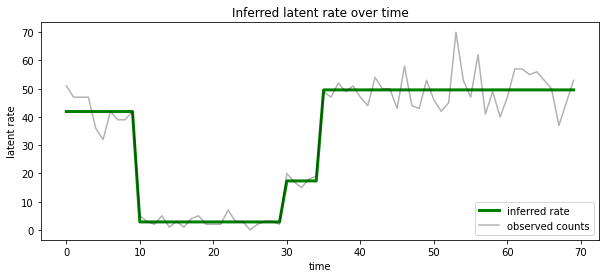
Неизвестное количество состояний
В реальных задачах мы можем не знать «истинного» числа состояний в моделируемой системе. Это не всегда может вызывать беспокойство: если вы не особо заботитесь об идентичности неизвестных состояний, вы можете просто запустить модель с большим количеством состояний, чем вы знаете, что модели потребуется, и выучить (что-то вроде) кучу дубликатов. копии актуальных состояний. Но давайте предположим, что вы действительно заботитесь об установлении «истинного» количества скрытых состояний.
Мы можем рассматривать это как случай выбора модели байесовского : у нас есть множество моделей - кандидатов, каждый из которых с различным числом скрытых состояний, и мы хотим , чтобы выбрать тот , который , скорее всего, породили наблюдаемые данные. Чтобы сделать это, мы вычислим предельную вероятность данных по каждой модели (можно также добавить до на самих моделях, но это не будет необходимости в этом анализе, в бритве байесовского Оккама оказывается достаточно , чтобы закодировать предпочтение более простым моделям).
К сожалению, истинная предельная вероятность того , что интегрирует более как дискретные состояния \(z_{1:T}\) и (вектор) параметры скорости \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) не сговорчивый для этой модели. Для удобства мы будем аппроксимировать его , используя так называемый « эмпирический Байес » или «тип максимального правдоподобия II» оценка: вместо того , чтобы полностью интегрировать из параметров (неизвестная) скорости \(\lambda\) , связанный с каждым состоянием системы, мы оптимизируем над их значениями:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
Это приближение может быть избыточным, т. Е. Оно будет отдавать предпочтение более сложным моделям, чем истинное предельное правдоподобие. Мы могли бы рассмотреть более верные приближения, например, оптимизируя вариационного нижнюю границу, или с помощью Монте - Карло оценивания , таких как отожженном выборки по значимости ; это (к сожалению) выходит за рамки этого ноутбука. (Более подробно о выборе модели байесовского и приближений, 7 -й главе превосходного машинного обучения: вероятностный перспектива является хорошим справочником.)
В принципе, мы могли бы сделать эту модель сравнение просто перезапустив оптимизации выше много раз с разными значениями num_states , но это было бы очень много работы. Здесь мы покажем , как рассмотреть несколько моделей параллельно, с использованием TFP в batch_shape механизм для векторизации.
Матрица перехода и начальное состояние до: вместо создания единого описания модели, теперь мы будем строить партию матриц перехода и предыдущего логит, по одному для каждого кандидата модели до max_num_states . Для упрощения пакетирования нам нужно убедиться, что все вычисления имеют одну и ту же «форму»: она должна соответствовать размерам самой большой модели, которую мы поместим. Для работы с более мелкими моделями мы можем «встроить» их описания в самые верхние измерения пространства состояний, эффективно обрабатывая остальные измерения как фиктивные состояния, которые никогда не используются.
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
Теперь действуем аналогично тому, как указано выше. На этот раз мы будем использовать дополнительный пакетный размер в trainable_rates отдельно соответствовать ценам для каждой рассматриваемой модели.
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
При вычислении общей логарифмической вероятности мы стараемся суммировать только априорные значения для ставок, фактически используемых каждым компонентом модели:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
Теперь мы оптимизируем пакетное цели мы сконструированный, подходят для всех моделей - кандидатов одновременно:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
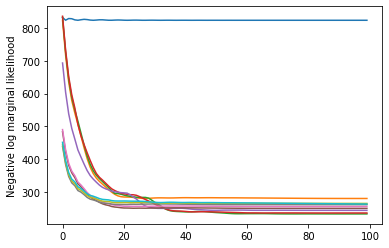
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
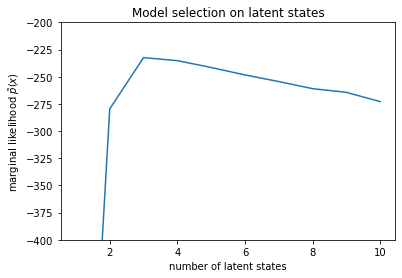
Изучая вероятности, мы видим, что (приблизительное) предельное правдоподобие имеет тенденцию предпочитать модель с тремя состояниями. Это кажется вполне правдоподобным - «истинная» модель имела четыре состояния, но, просто взглянув на данные, трудно исключить объяснение с тремя состояниями.
Мы также можем извлечь ставки, подходящие для каждой модели кандидата:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
И нанесите на график объяснения, которые каждая модель предоставляет данным:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
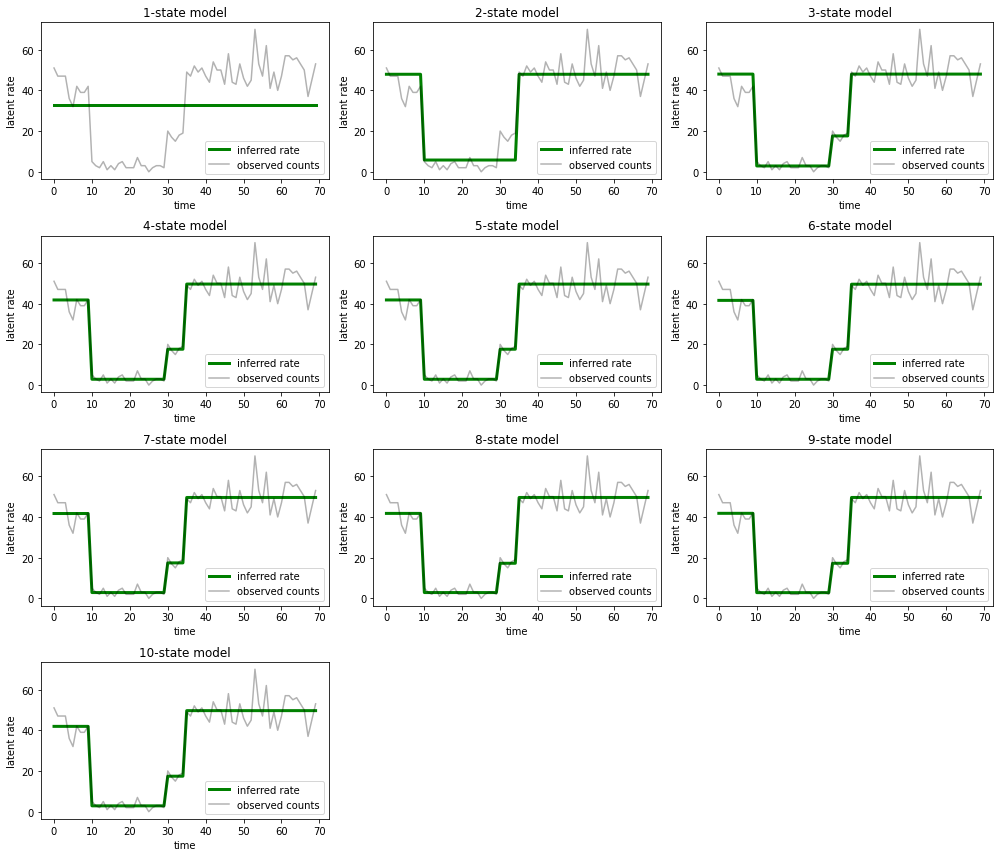
Легко увидеть, как модели с одним, двумя и (более тонко) с тремя состояниями дают неадекватные объяснения. Интересно, что все модели выше четырех состояний дают, по сути, одно и то же объяснение! Вероятно, это связано с тем, что наши «данные» относительно чисты и не оставляют места для альтернативных объяснений; на более беспорядочных реальных данных мы ожидаем, что модели с большей емкостью будут постепенно обеспечивать лучшее соответствие данным, с некоторым компромиссом, когда улучшенное соответствие перевешивается сложностью модели.
Расширения
Модели в этом ноутбуке можно легко расширить во многих отношениях. Например:
- позволяя скрытым состояниям иметь разные вероятности (некоторые состояния могут быть обычными или редкими)
- разрешение неравномерных переходов между скрытыми состояниями (например, чтобы узнать, что за отказом машины обычно следует перезагрузка системы, обычно следует период хорошей производительности и т. д.)
- другие модели выбросов, например
NegativeBinomialдля моделирования изменения дисперсии в учетных данных или непрерывных распределений , таких какNormalдля вещественных данных.
