The intent of this notebook is to help TFP 0.13.0 "come to life" via some small snippets - little demos of things you can achieve with TFP.
 View on TensorFlow.org View on TensorFlow.org
|
 Run in Google Colab Run in Google Colab
|
 View source on GitHub View source on GitHub
|
 Download notebook Download notebook
|
Installs & imports
!pip3 install -qU tensorflow==2.5.0 tensorflow_probability==0.13.0 tensorflow-datasets inference_gym
import tensorflow as tf
import tensorflow_probability as tfp
assert '0.13' in tfp.__version__, tfp.__version__
assert '2.5' in tf.__version__, tf.__version__
physical_devices = tf.config.list_physical_devices('CPU')
tf.config.set_logical_device_configuration(
physical_devices[0],
[tf.config.LogicalDeviceConfiguration(),
tf.config.LogicalDeviceConfiguration()])
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
import matplotlib.pyplot as plt
import numpy as np
import scipy.interpolate
import IPython
import seaborn as sns
import logging
|████████████████████████████████| 5.4MB 8.8MB/s
|████████████████████████████████| 3.9MB 37.1MB/s
|████████████████████████████████| 296kB 31.6MB/s
Distributions [core math]
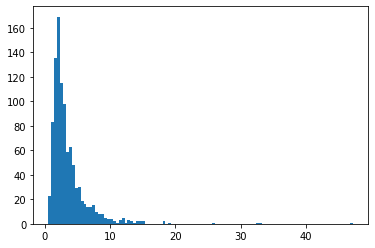
BetaQuotient
Ratio of two independent Beta-distributed random variables
plt.hist(tfd.BetaQuotient(concentration1_numerator=5.,
concentration0_numerator=2.,
concentration1_denominator=3.,
concentration0_denominator=8.).sample(1_000, seed=(1, 23)),
bins='auto');
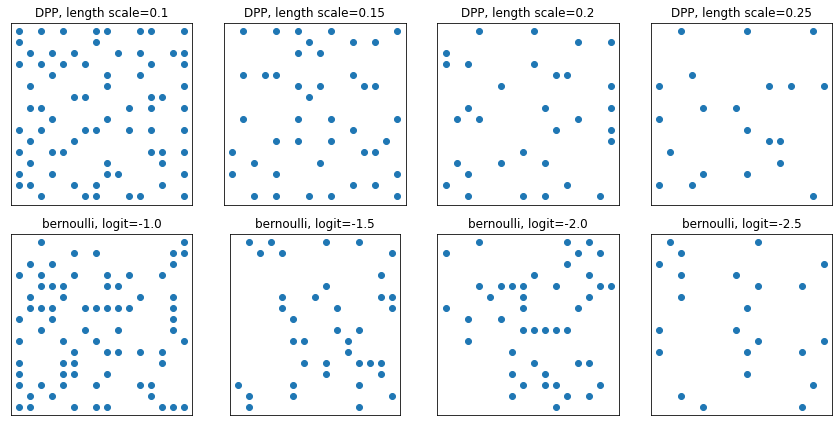
DeterminantalPointProcess
Distribution over subsets (represented as one-hot) of a given set. Samples follow a repulsivity property (probabilities are proportional to the volume spanned by vectors corresponding to the selected subset of points), which tends toward sampling diverse subsets. [Compare against i.i.d. Bernoulli samples.]
grid_size = 16
# Generate grid_size**2 pts on the unit square.
grid = np.arange(0, 1, 1./grid_size).astype(np.float32)
import itertools
points = np.array(list(itertools.product(grid, grid)))
# Create the kernel L that parameterizes the DPP.
kernel_amplitude = 2.
kernel_lengthscale = [.1, .15, .2, .25] # Increasing length scale indicates more points are "nearby", tending toward smaller subsets.
kernel = tfpk.ExponentiatedQuadratic(kernel_amplitude, kernel_lengthscale)
kernel_matrix = kernel.matrix(points, points)
eigenvalues, eigenvectors = tf.linalg.eigh(kernel_matrix)
dpp = tfd.DeterminantalPointProcess(eigenvalues, eigenvectors)
print(dpp)
# The inner-most dimension of the result of `dpp.sample` is a multi-hot
# encoding of a subset of {1, ..., ground_set_size}.
# We will compare against a bernoulli distribution.
samps_dpp = dpp.sample(seed=(1, 2)) # 4 x grid_size**2
logits = tf.broadcast_to([[-1.], [-1.5], [-2], [-2.5]], [4, grid_size**2])
samps_bern = tfd.Bernoulli(logits=logits).sample(seed=(2, 3))
plt.figure(figsize=(12, 6))
for i, (samp, samp_bern) in enumerate(zip(samps_dpp, samps_bern)):
plt.subplot(241 + i)
plt.scatter(*points[np.where(samp)].T)
plt.title(f'DPP, length scale={kernel_lengthscale[i]}')
plt.xticks([])
plt.yticks([])
plt.gca().set_aspect(1.)
plt.subplot(241 + i + 4)
plt.scatter(*points[np.where(samp_bern)].T)
plt.title(f'bernoulli, logit={logits[i,0]}')
plt.xticks([])
plt.yticks([])
plt.gca().set_aspect(1.)
plt.tight_layout()
plt.show()
tfp.distributions.DeterminantalPointProcess("DeterminantalPointProcess", batch_shape=[4], event_shape=[256], dtype=int32)
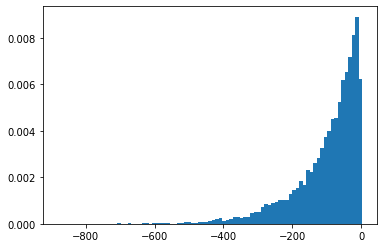
SigmoidBeta
Log-odds of two gamma distributions. More numerically stable sample space than Beta.
plt.hist(tfd.SigmoidBeta(concentration1=.01, concentration0=2.).sample(10_000, seed=(1, 23)),
bins='auto', density=True);
plt.show()
print('Old way, fractions non-finite:')
print(np.sum(~tf.math.is_finite(
tfb.Invert(tfb.Sigmoid())(tfd.Beta(concentration1=.01, concentration0=2.)).sample(10_000, seed=(1, 23)))) / 10_000)
print(np.sum(~tf.math.is_finite(
tfb.Invert(tfb.Sigmoid())(tfd.Beta(concentration1=2., concentration0=.01)).sample(10_000, seed=(2, 34)))) / 10_000)
Old way, fractions non-finite: 0.4215 0.8624
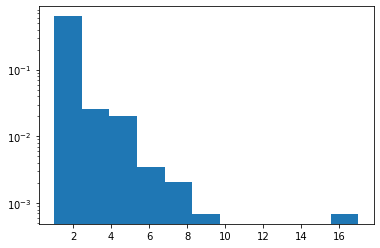
Zipf
Added JAX support.
plt.hist(tfd.Zipf(3.).sample(1_000, seed=(12, 34)).numpy(), bins='auto', density=True, log=True);
NormalInverseGaussian
Flexible parametric family that supports heavy tails, skewed, and vanilla Normal.
MatrixNormalLinearOperator
Matrix Normal distribution.
# Initialize a single 2 x 3 Matrix Normal.
mu = [[1., 2, 3], [3., 4, 5]]
col_cov = [[ 0.36, 0.12, 0.06],
[ 0.12, 0.29, -0.13],
[ 0.06, -0.13, 0.26]]
scale_column = tf.linalg.LinearOperatorLowerTriangular(tf.linalg.cholesky(col_cov))
scale_row = tf.linalg.LinearOperatorDiag([0.9, 0.8])
mvn = tfd.MatrixNormalLinearOperator(loc=mu, scale_row=scale_row, scale_column=scale_column)
mvn.sample()
WARNING:tensorflow:From /usr/local/lib/python3.7/dist-packages/tensorflow/python/ops/linalg/linear_operator_kronecker.py:224: LinearOperator.graph_parents (from tensorflow.python.ops.linalg.linear_operator) is deprecated and will be removed in a future version.
Instructions for updating:
Do not call `graph_parents`.
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[1.2495145, 1.549366 , 3.2748342],
[3.7330258, 4.3413105, 4.83423 ]], dtype=float32)>
MatrixStudentTLinearOperator
Matrix T distribution.
mu = [[1., 2, 3], [3., 4, 5]]
col_cov = [[ 0.36, 0.12, 0.06],
[ 0.12, 0.29, -0.13],
[ 0.06, -0.13, 0.26]]
scale_column = tf.linalg.LinearOperatorLowerTriangular(tf.linalg.cholesky(col_cov))
scale_row = tf.linalg.LinearOperatorDiag([0.9, 0.8])
mvn = tfd.MatrixTLinearOperator(
df=2.,
loc=mu,
scale_row=scale_row,
scale_column=scale_column)
mvn.sample()
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[1.6549466, 2.6708362, 2.8629923],
[2.1222284, 3.6904747, 5.08014 ]], dtype=float32)>
Distributions [software / wrappers]
Sharded
Shards independent event portions of a distribution across multiple processors. Aggregates log_prob across devices, handles gradients in concert with tfp.experimental.distribute.JointDistribution*. Much more in the Distributed Inference notebook.
strategy = tf.distribute.MirroredStrategy()
@tf.function
def sample_and_lp(seed):
d = tfp.experimental.distribute.Sharded(tfd.Normal(0, 1))
s = d.sample(seed=seed)
return s, d.log_prob(s)
strategy.run(sample_and_lp, args=(tf.constant([12,34]),))
WARNING:tensorflow:There are non-GPU devices in `tf.distribute.Strategy`, not using nccl allreduce.
WARNING:tensorflow:Collective ops is not configured at program startup. Some performance features may not be enabled.
INFO:tensorflow:Using MirroredStrategy with devices ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1')
INFO:tensorflow:Reduce to /job:localhost/replica:0/task:0/device:CPU:0 then broadcast to ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1').
(PerReplica:{
0: <tf.Tensor: shape=(), dtype=float32, numpy=0.0051413667>,
1: <tf.Tensor: shape=(), dtype=float32, numpy=-0.3393052>
}, PerReplica:{
0: <tf.Tensor: shape=(), dtype=float32, numpy=-1.8954543>,
1: <tf.Tensor: shape=(), dtype=float32, numpy=-1.8954543>
})
BatchBroadcast
Implicitly broadcast the batch dimensions of an underlying distribution with or to a given batch shape.
underlying = tfd.MultivariateNormalDiag(tf.zeros([7, 1, 5]), tf.ones([5]))
print('underlying:', underlying)
d = tfd.BatchBroadcast(underlying, [8, 1, 6])
print('broadcast [7, 1] *with* [8, 1, 6]:', d)
try:
tfd.BatchBroadcast(underlying, to_shape=[8, 1, 6])
except ValueError as e:
print('broadcast [7, 1] *to* [8, 1, 6] is invalid:', e)
d = tfd.BatchBroadcast(underlying, to_shape=[8, 7, 6])
print('broadcast [7, 1] *to* [8, 7, 6]:', d)
underlying: tfp.distributions.MultivariateNormalDiag("MultivariateNormalDiag", batch_shape=[7, 1], event_shape=[5], dtype=float32)
broadcast [7, 1] *with* [8, 1, 6]: tfp.distributions.BatchBroadcast("BatchBroadcastMultivariateNormalDiag", batch_shape=[8, 7, 6], event_shape=[5], dtype=float32)
broadcast [7, 1] *to* [8, 1, 6] is invalid: Argument `to_shape` ([8 1 6]) is incompatible with underlying distribution batch shape ((7, 1)).
broadcast [7, 1] *to* [8, 7, 6]: tfp.distributions.BatchBroadcast("BatchBroadcastMultivariateNormalDiag", batch_shape=[8, 7, 6], event_shape=[5], dtype=float32)
Masked
For single-program/multiple-data or sparse-as-masked-dense use-cases, a distribution that masks out the log_prob of invalid underlying distributions.
d = tfd.Masked(tfd.Normal(tf.zeros([7]), 1),
validity_mask=tf.sequence_mask([3, 4], 7))
print(d.log_prob(d.sample(seed=(1, 1))))
d = tfd.Masked(tfd.Normal(0, 1),
validity_mask=[False, True, False],
safe_sample_fn=tfd.Distribution.mode)
print(d.log_prob(d.sample(seed=(2, 2))))
tf.Tensor( [[-2.3054113 -1.8524303 -1.2220721 0. 0. 0. 0. ] [-1.118623 -1.1370811 -1.1574132 -5.884986 0. 0. 0. ]], shape=(2, 7), dtype=float32) tf.Tensor([ 0. -0.93683904 0. ], shape=(3,), dtype=float32)
Bijectors
- Bijectors
- Add bijectors to mimic
tf.nest.flatten(tfb.tree_flatten) andtf.nest.pack_sequence_as(tfb.pack_sequence_as). - Adds
tfp.experimental.bijectors.Sharded - Remove deprecated
tfb.ScaleTrilL. Usetfb.FillScaleTriLinstead. - Adds
cls.parameter_properties()annotations for Bijectors. - Extend range
tfb.Powerto all reals for odd integer powers. - Infer the log-deg-jacobian of scalar bijectors using autodiff, if not otherwise specified.
- Add bijectors to mimic
Restructuring bijectors
ex = (tf.constant(1.), dict(b=tf.constant(2.), c=tf.constant(3.)))
b = tfb.tree_flatten(ex)
print(b.forward(ex))
print(b.inverse(list(tf.constant([1., 2, 3]))))
b = tfb.pack_sequence_as(ex)
print(b.forward(list(tf.constant([1., 2, 3]))))
print(b.inverse(ex))
[<tf.Tensor: shape=(), dtype=float32, numpy=1.0>, <tf.Tensor: shape=(), dtype=float32, numpy=2.0>, <tf.Tensor: shape=(), dtype=float32, numpy=3.0>]
(<tf.Tensor: shape=(), dtype=float32, numpy=1.0>, {'b': <tf.Tensor: shape=(), dtype=float32, numpy=2.0>, 'c': <tf.Tensor: shape=(), dtype=float32, numpy=3.0>})
(<tf.Tensor: shape=(), dtype=float32, numpy=1.0>, {'b': <tf.Tensor: shape=(), dtype=float32, numpy=2.0>, 'c': <tf.Tensor: shape=(), dtype=float32, numpy=3.0>})
[<tf.Tensor: shape=(), dtype=float32, numpy=1.0>, <tf.Tensor: shape=(), dtype=float32, numpy=2.0>, <tf.Tensor: shape=(), dtype=float32, numpy=3.0>]
Sharded
SPMD reduction in log-determinant. See Sharded in Distributions, below.
strategy = tf.distribute.MirroredStrategy()
def sample_lp_logdet(seed):
d = tfd.TransformedDistribution(tfp.experimental.distribute.Sharded(tfd.Normal(0, 1), shard_axis_name='i'),
tfp.experimental.bijectors.Sharded(tfb.Sigmoid(), shard_axis_name='i'))
s = d.sample(seed=seed)
return s, d.log_prob(s), d.bijector.inverse_log_det_jacobian(s)
strategy.run(sample_lp_logdet, (tf.constant([1, 2]),))
WARNING:tensorflow:There are non-GPU devices in `tf.distribute.Strategy`, not using nccl allreduce.
WARNING:tensorflow:Collective ops is not configured at program startup. Some performance features may not be enabled.
INFO:tensorflow:Using MirroredStrategy with devices ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1')
WARNING:tensorflow:Using MirroredStrategy eagerly has significant overhead currently. We will be working on improving this in the future, but for now please wrap `call_for_each_replica` or `experimental_run` or `run` inside a tf.function to get the best performance.
INFO:tensorflow:Reduce to /job:localhost/replica:0/task:0/device:CPU:0 then broadcast to ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1').
INFO:tensorflow:Reduce to /job:localhost/replica:0/task:0/device:CPU:0 then broadcast to ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1').
(PerReplica:{
0: <tf.Tensor: shape=(), dtype=float32, numpy=0.87746525>,
1: <tf.Tensor: shape=(), dtype=float32, numpy=0.24580425>
}, PerReplica:{
0: <tf.Tensor: shape=(), dtype=float32, numpy=-0.48870325>,
1: <tf.Tensor: shape=(), dtype=float32, numpy=-0.48870325>
}, PerReplica:{
0: <tf.Tensor: shape=(), dtype=float32, numpy=3.9154015>,
1: <tf.Tensor: shape=(), dtype=float32, numpy=3.9154015>
})
VI
- Adds
build_split_flow_surrogate_posteriortotfp.experimental.vito build structured VI surrogate posteriors from normalizing flows. - Adds
build_affine_surrogate_posteriortotfp.experimental.vifor construction of ADVI surrogate posteriors from an event shape. - Adds
build_affine_surrogate_posterior_from_base_distributiontotfp.experimental.vito enable construction of ADVI surrogate posteriors with correlation structures induced by affine transformations.
VI/MAP/MLE
- Added convenience method
tfp.experimental.util.make_trainable(cls)to create trainable instances of distributions and bijectors.
d = tfp.experimental.util.make_trainable(tfd.Gamma)
print(d.trainable_variables)
print(d)
(<tf.Variable 'Gamma_trainable_variables/concentration:0' shape=() dtype=float32, numpy=1.0296053>, <tf.Variable 'Gamma_trainable_variables/log_rate:0' shape=() dtype=float32, numpy=-0.3465951>)
tfp.distributions.Gamma("Gamma", batch_shape=[], event_shape=[], dtype=float32)
MCMC
- MCMC diagnostics support arbitrary structures of states, not just lists.
remc_thermodynamic_integralsadded totfp.experimental.mcmc- Adds
tfp.experimental.mcmc.windowed_adaptive_hmc - Adds an experimental API for initializing a Markov chain from a near-zero uniform distribution in unconstrained space.
tfp.experimental.mcmc.init_near_unconstrained_zero - Adds an experimental utility for retrying Markov Chain initialization until an acceptable point is found.
tfp.experimental.mcmc.retry_init - Shuffling experimental streaming MCMC API to slot into tfp.mcmc with a minimum of disruption.
- Adds
ThinningKerneltoexperimental.mcmc. - Adds
experimental.mcmc.run_kerneldriver as a candidate streaming-based replacement tomcmc.sample_chain
init_near_unconstrained_zero, retry_init
@tfd.JointDistributionCoroutine
def model():
Root = tfd.JointDistributionCoroutine.Root
c0 = yield Root(tfd.Gamma(2, 2, name='c0'))
c1 = yield Root(tfd.Gamma(2, 2, name='c1'))
counts = yield tfd.Sample(tfd.BetaBinomial(23, c1, c0), 10, name='counts')
jd = model.experimental_pin(counts=model.sample(seed=[20, 30]).counts)
init_dist = tfp.experimental.mcmc.init_near_unconstrained_zero(jd)
print(init_dist)
tfp.experimental.mcmc.retry_init(init_dist.sample, jd.unnormalized_log_prob)
tfp.distributions.TransformedDistribution("default_joint_bijectorrestructureJointDistributionSequential", batch_shape=StructTuple(
c0=[],
c1=[]
), event_shape=StructTuple(
c0=[],
c1=[]
), dtype=StructTuple(
c0=float32,
c1=float32
))
StructTuple(
c0=<tf.Tensor: shape=(), dtype=float32, numpy=1.7879653>,
c1=<tf.Tensor: shape=(), dtype=float32, numpy=0.34548905>
)
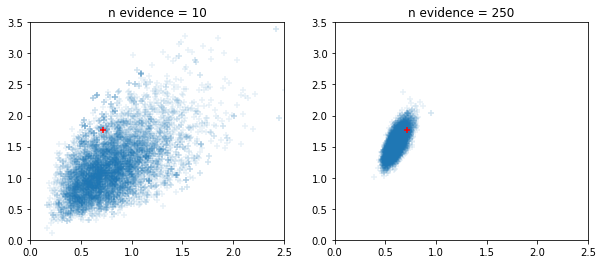
Windowed adaptive HMC and NUTS samplers
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
for i, n_evidence in enumerate((10, 250)):
ax[i].set_title(f'n evidence = {n_evidence}')
ax[i].set_xlim(0, 2.5); ax[i].set_ylim(0, 3.5)
@tfd.JointDistributionCoroutine
def model():
Root = tfd.JointDistributionCoroutine.Root
c0 = yield Root(tfd.Gamma(2, 2, name='c0'))
c1 = yield Root(tfd.Gamma(2, 2, name='c1'))
counts = yield tfd.Sample(tfd.BetaBinomial(23, c1, c0), n_evidence, name='counts')
s = model.sample(seed=[20, 30])
print(s)
jd = model.experimental_pin(counts=s.counts)
states, trace = tf.function(tfp.experimental.mcmc.windowed_adaptive_hmc)(
100, jd, num_leapfrog_steps=5, seed=[100, 200])
ax[i].scatter(states.c0.numpy().reshape(-1), states.c1.numpy().reshape(-1),
marker='+', alpha=.1)
ax[i].scatter(s.c0, s.c1, marker='+', color='r')
StructTuple(
c0=<tf.Tensor: shape=(), dtype=float32, numpy=0.7161876>,
c1=<tf.Tensor: shape=(), dtype=float32, numpy=1.7696666>,
counts=<tf.Tensor: shape=(10,), dtype=float32, numpy=array([ 6., 10., 23., 7., 2., 20., 14., 16., 22., 17.], dtype=float32)>
)
WARNING:tensorflow:6 out of the last 6 calls to <function windowed_adaptive_hmc at 0x7fda42bed8c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has reduce_retracing=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
StructTuple(
c0=<tf.Tensor: shape=(), dtype=float32, numpy=0.7161876>,
c1=<tf.Tensor: shape=(), dtype=float32, numpy=1.7696666>,
counts=<tf.Tensor: shape=(250,), dtype=float32, numpy=
array([ 6., 10., 23., 7., 2., 20., 14., 16., 22., 17., 22., 21., 6.,
21., 12., 22., 23., 16., 18., 21., 16., 17., 17., 16., 21., 14.,
23., 15., 10., 19., 8., 23., 23., 14., 1., 23., 16., 22., 20.,
20., 22., 15., 16., 20., 20., 21., 23., 22., 21., 15., 18., 23.,
12., 16., 19., 23., 18., 5., 22., 22., 22., 18., 12., 17., 17.,
16., 8., 22., 20., 23., 3., 12., 14., 18., 7., 19., 19., 9.,
10., 23., 14., 22., 22., 21., 13., 23., 14., 23., 10., 17., 23.,
17., 20., 16., 20., 19., 14., 0., 17., 22., 12., 2., 17., 15.,
14., 23., 19., 15., 23., 2., 21., 23., 21., 7., 21., 12., 23.,
17., 17., 4., 22., 16., 14., 19., 19., 20., 6., 16., 14., 18.,
21., 12., 21., 21., 22., 2., 19., 11., 6., 19., 1., 23., 23.,
14., 6., 23., 18., 8., 20., 23., 13., 20., 18., 23., 17., 22.,
23., 20., 18., 22., 16., 23., 9., 22., 21., 16., 20., 21., 16.,
23., 7., 13., 23., 19., 3., 13., 23., 23., 13., 19., 23., 20.,
18., 8., 19., 14., 12., 6., 8., 23., 3., 13., 21., 23., 22.,
23., 19., 22., 21., 15., 22., 21., 21., 23., 9., 19., 20., 23.,
11., 23., 14., 23., 14., 21., 21., 10., 23., 9., 13., 1., 8.,
8., 20., 21., 21., 21., 14., 16., 16., 9., 23., 22., 11., 23.,
12., 18., 1., 23., 9., 3., 21., 21., 23., 22., 18., 23., 16.,
3., 11., 16.], dtype=float32)>
)
Math, stats
Math/linalg
- Add
tfp.math.trapzfor trapezoidal integration. - Add
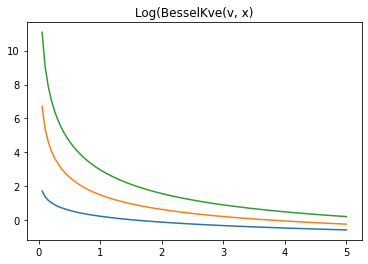
tfp.math.log_bessel_kve. - Add
no_pivot_ldltoexperimental.linalg. - Add
marginal_fnargument toGaussianProcess(seeno_pivot_ldl). - Added
tfp.math.atan_difference(x, y) - Add
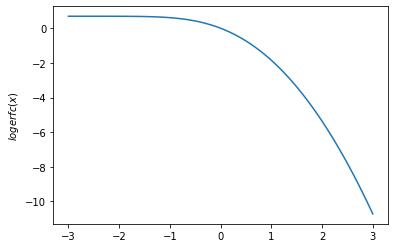
tfp.math.erfcx,tfp.math.logerfcandtfp.math.logerfcx - Add
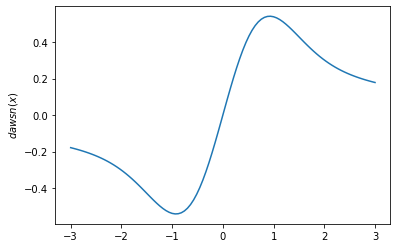
tfp.math.dawsnfor Dawson's Integral. - Add
tfp.math.igammaincinv,tfp.math.igammacinv. - Add
tfp.math.sqrt1pm1. - Add
LogitNormal.stddev_approxandLogitNormal.variance_approx - Add
tfp.math.owens_tfor the Owen's T function. - Add
bracket_rootmethod to automatically initialize bounds for a root search. - Add Chandrupatla's method for finding roots of scalar functions.
- Add
Stats
tfp.stats.windowed_meanefficiently computes windowed means.tfp.stats.windowed_varianceefficiently and accurately computes windowed variances.tfp.stats.cumulative_varianceefficiently and accurately computes cumulative variances.RunningCovarianceand friends can now be initialized from an example Tensor, not just from explicit shape and dtype.- Cleaner API for
RunningCentralMoments,RunningMean,RunningPotentialScaleReduction.
Owen's T, Erfcx, Logerfc, Logerfcx, Dawson functions
# Owen's T gives the probability that X > h, 0 < Y < a * X. Let's check that
# with random sampling.
h = np.array([1., 2.]).astype(np.float32)
a = np.array([10., 11.5]).astype(np.float32)
probs = tfp.math.owens_t(h, a)
x = tfd.Normal(0., 1.).sample(int(1e5), seed=(6, 245)).numpy()
y = tfd.Normal(0., 1.).sample(int(1e5), seed=(7, 245)).numpy()
true_values = (
(x[..., np.newaxis] > h) &
(0. < y[..., np.newaxis]) &
(y[..., np.newaxis] < a * x[..., np.newaxis]))
print('Calculated values: {}'.format(
np.count_nonzero(true_values, axis=0) / 1e5))
print('Expected values: {}'.format(probs))
Calculated values: [0.07896 0.01134] Expected values: [0.07932763 0.01137507]
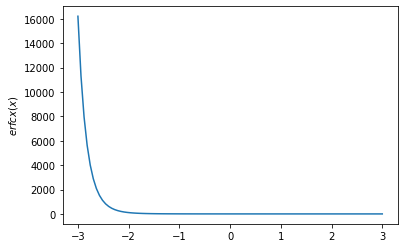
x = np.linspace(-3., 3., 100)
plt.plot(x, tfp.math.erfcx(x))
plt.ylabel('$erfcx(x)$')
plt.show()
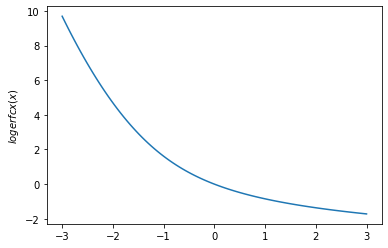
plt.plot(x, tfp.math.logerfcx(x))
plt.ylabel('$logerfcx(x)$')
plt.show()
plt.plot(x, tfp.math.logerfc(x))
plt.ylabel('$logerfc(x)$')
plt.show()
plt.plot(x, tfp.math.dawsn(x))
plt.ylabel('$dawsn(x)$')
plt.show()
igammainv / igammacinv
# Igammainv and Igammacinv are inverses to Igamma and Igammac
x = np.linspace(1., 10., 10)
y = tf.math.igamma(0.3, x)
x_prime = tfp.math.igammainv(0.3, y)
print('x: {}'.format(x))
print('igammainv(igamma(a, x)):\n {}'.format(x_prime))
y = tf.math.igammac(0.3, x)
x_prime = tfp.math.igammacinv(0.3, y)
print('\n')
print('x: {}'.format(x))
print('igammacinv(igammac(a, x)):\n {}'.format(x_prime))
x: [ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.] igammainv(igamma(a, x)): [1. 1.9999992 3.000003 4.0000024 5.0000257 5.999887 7.0002484 7.999243 8.99872 9.994673 ] x: [ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.] igammacinv(igammac(a, x)): [1. 2. 3. 4. 5. 6. 7. 8.000001 9. 9.999999]
log-kve
x = np.linspace(0., 5., 100)
for v in [0.5, 2., 3]:
plt.plot(x, tfp.math.log_bessel_kve(v, x).numpy())
plt.title('Log(BesselKve(v, x)')
Text(0.5, 1.0, 'Log(BesselKve(v, x)')
Other
STS
- Speed up STS forecasting and decomposition using internal
tf.functionwrapping. - Add option to speed up filtering in
LinearGaussianSSMwhen only the final step's results are required. - Variational Inference with joint distributions: example notebook with the Radon model.
- Add experimental support for transforming any distribution into a preconditioning bijector.
- Speed up STS forecasting and decomposition using internal
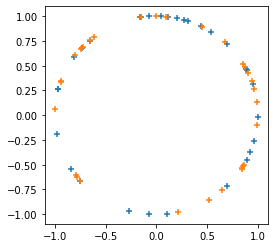
Adds
tfp.random.sanitize_seed.
plt.figure(figsize=(4, 4))
seed = tfp.random.sanitize_seed(123)
seed1, seed2 = tfp.random.split_seed(seed)
samps = tfp.random.spherical_uniform([30], dimension=2, seed=seed1)
plt.scatter(*samps.numpy().T, marker='+')
samps = tfp.random.spherical_uniform([30], dimension=2, seed=seed2)
plt.scatter(*samps.numpy().T, marker='+');