 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запускаем в Google Colab Запускаем в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
Я написал этот блокнот в качестве примера для изучения TensorFlow Probability. Проблема, которую я решил решить, - это оценка ковариационной матрицы для выборок двумерной гауссовской случайной величины со средним 0. У проблемы есть несколько приятных особенностей:
- Если мы используем обратный априор Уишарта для ковариации (общий подход), проблема имеет аналитическое решение, поэтому мы можем проверить наши результаты.
- Проблема включает выборку ограниченного параметра, что добавляет интересную сложность.
- Самое простое решение - не самое быстрое, поэтому необходимо провести некоторую оптимизацию.
Я решил описать свой опыт по ходу дела. Мне потребовалось некоторое время, чтобы осмыслить тонкости TFP, так что этот ноутбук запускается довольно просто, а затем постепенно переходит к более сложным функциям TFP. По пути я столкнулся с множеством проблем и попытался уловить как процессы, которые помогли мне их идентифицировать, так и обходные пути, которые я в итоге нашел. Я попытался включить много деталей ( в том числе много тестов , чтобы убедиться , что отдельные шаги правильны).
Зачем изучать вероятность TensorFlow?
Я нашел TensorFlow Probability привлекательным для моего проекта по нескольким причинам:
- Вероятность TensorFlow позволяет создавать прототипы сложных моделей в интерактивном режиме в записной книжке. Вы можете разбить свой код на небольшие части, которые можно тестировать в интерактивном режиме и с помощью модульных тестов.
- Когда вы будете готовы к масштабированию, вы сможете воспользоваться преимуществами всей инфраструктуры, которая у нас есть для запуска TensorFlow на нескольких оптимизированных процессорах на нескольких машинах.
- Наконец, хотя мне очень нравится Стэн, мне довольно сложно отлаживать его. Вы должны написать весь свой код моделирования на отдельном языке, который имеет очень мало инструментов, позволяющих вам тыкать в свой код, проверять промежуточные состояния и так далее.
Обратной стороной является то, что TensorFlow Probability намного новее, чем Stan и PyMC3, поэтому документация находится в стадии разработки, и есть много функций, которые еще предстоит создать. К счастью, я обнаружил, что фундамент TFP прочный, и он спроектирован по модульному принципу, что позволяет довольно просто расширять его функциональные возможности. В этой записной книжке, помимо решения тематического исследования, я покажу несколько способов расширения TFP.
Для кого это
Я предполагаю, что читатели приходят к этой записной книжке с некоторыми важными предпосылками. Вам следует:
- Знать основы байесовского вывода. (Если вы этого не сделаете, действительно хорошая первая книга Статистическая Переосмысление )
- Есть некоторое знакомство с библиотекой выборки MCMC, например Стан / PyMC3 / ОШИБКИ
- Есть твердое понимание NumPy (Один хороший интро Python для анализа данных )
- Есть по крайней мере прохождения знакомство с TensorFlow , но не обязательно опыт. ( Обучение TensorFlow это хорошо, но быстрые пути эволюции TensorFlow, что большинство книг будут немного устаревшие. Стэнфорд CS20 конечно тоже хорошо.)
Первая попытка
Вот моя первая попытка решить проблему. Спойлер: мое решение не работает, и потребуется несколько попыток, чтобы все исправить! Хотя этот процесс занимает некоторое время, каждая из приведенных ниже попыток была полезна для изучения новой части TFP.
Одно примечание: в настоящее время TFP не реализует обратное распределение Уишарта (в конце мы увидим, как развернуть собственное обратное распределение Уишарта), поэтому вместо этого я заменю задачу на оценку матрицы точности с использованием априорного распределения Уишарта.
import collections
import math
import os
import time
import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
Шаг 1: соберите все наблюдения вместе
Все мои данные здесь синтетические, так что это покажется немного более аккуратным, чем реальный пример. Однако нет причин, по которым вы не можете генерировать собственные синтетические данные.
Совет: После того как вы определились с формой вашей модели, вы можете выбрать некоторые значения параметров и использовать выбранную модель для создания некоторых данных синтетических. В качестве проверки работоспособности вашей реализации вы можете затем убедиться, что ваши оценки включают истинные значения выбранных вами параметров. Чтобы ускорить цикл отладки / тестирования, вы можете рассмотреть упрощенную версию вашей модели (например, использовать меньшее количество измерений или меньшее количество образцов).
Совет: Это проще всего работать с вашими наблюдениями как NumPy массивы. Важно отметить, что NumPy по умолчанию использует float64, тогда как TensorFlow по умолчанию использует float32.
Как правило, операции TensorFlow хотят, чтобы все аргументы имели один и тот же тип, и вам необходимо выполнить явное приведение данных для изменения типов. Если вы используете наблюдения float64, вам нужно будет добавить много операций приведения. NumPy, напротив, позаботится о преобразовании автоматически. Следовательно, гораздо проще преобразовать данные Numpy в float32 , чем заставить TensorFlow для использования float64.
Выберите некоторые значения параметров
# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)
# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))
[[4. 1.8] [1.8 1. ]] eigenvalues: [4.843075 0.15692513]
Произведите синтетические наблюдения
Обратите внимание , что TensorFlow вероятность использует соглашение , что начальный размер (ы) данных представляют примеры показателей, а окончательный размер (ы) данных представляет размерность ваших образцов.
Здесь мы хотим 100 образцов, каждый из которых представляет собой вектор длины 2. Мы будем генерировать массив my_data с формой (100, 2). my_data[i, :] является \(i\)го образца, и он представляет собой вектор длины 2.
( Не забудьте сделать my_data иметь тип float32!)
# Set the seed so the results are reproducible.
np.random.seed(123)
# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
mean=true_mean, cov=true_cov, size=100,
check_valid='ignore').astype(np.float32)
my_data.shape
(100, 2)
Вменяемость проверьте наблюдения
Один из потенциальных источников ошибок - испортить ваши синтетические данные! Сделаем несколько простых проверок.
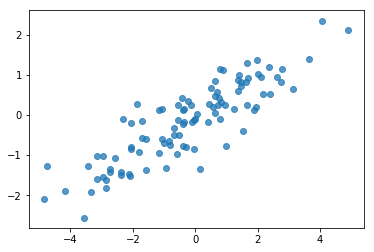
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()
print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)
mean of observations: [-0.24009615 -0.16638893] true mean: [0. 0.]
print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)
covariance of observations: [[3.95307734 1.68718486] [1.68718486 0.94910269]] true covariance: [[4. 1.8] [1.8 1. ]]
Хорошо, наши образцы выглядят разумно. Следующий шаг.
Шаг 2. Реализуйте функцию правдоподобия в NumPy
Главное, что нам нужно будет написать для выполнения выборки MCMC в TF Probability, - это функция правдоподобия журнала. В общем, написать TF немного сложнее, чем NumPy, поэтому я считаю полезным выполнить первоначальную реализацию в NumPy. Я собираюсь разделить функции правдоподобия на 2 части, функция правдоподобия данных, соответствует \(P(data | parameters)\) и предшествующей функции правдоподобия , которая соответствует \(P(parameters)\).
Обратите внимание, что эти функции NumPy не должны быть супероптимизированы / векторизованы, поскольку цель состоит в том, чтобы просто сгенерировать некоторые значения для тестирования. Правильность - ключевое соображение!
Сначала мы реализуем часть вероятности журнала данных. Это довольно просто. Единственное, что нужно помнить, это то, что мы собираемся работать с матрицами точности, поэтому мы параметризуем соответственно.
def log_lik_data_numpy(precision, data):
# np.linalg.inv is a really inefficient way to get the covariance matrix, but
# remember we don't care about speed here
cov = np.linalg.inv(precision)
rv = scipy.stats.multivariate_normal(true_mean, cov)
return np.sum(rv.logpdf(data))
# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)
-280.81822950593767
Мы будем использовать Уишарт до прецизионной матрицы , так как существует аналитическое решение для заднего (см удобного стола Википедии сопряженных настоятелей ).
Распределение Уишарта имеет 2 параметра:
- число степеней свободы (помеченный \(\nu\) в Википедии)
- шкала матрица (помеченный \(V\) в Википедии)
Среднее для распределения Уишарта с параметрами \(\nu, V\) является \(E[W] = \nu V\), а дисперсия является \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)
Некоторые полезные интуиции: Вы можете создать образец Уишарта пути создания \(\nu\) независимо рисует \(x_1 \ldots x_{\nu}\) из многовариантных нормальных случайных переменных со средним значением 0 и ковариационной \(V\) , а затем формированием суммы \(W = \sum_{i=1}^{\nu} x_i x_i^T\).
Если вы отмасштабировать образцы Уишарт путем деления их на \(\nu\), вы получите образец ковариационной матрицы \(x_i\). Этот образец ковариационная матрица должна стремиться к \(V\) как \(\nu\) увеличивается. Когда \(\nu\) мал, существует множество вариаций в образце ковариационной матрицы, так что малые значения \(\nu\) соответствует более слабым Настоятелям и большим значениям \(\nu\) соответствует более сильным априорным. Обратите внимание , что \(\nu\) должно быть по крайней мере , столь же большим как размерность пространства сэмплирования или вы будете генерировать вырожденные матрицы.
Мы будем использовать \(\nu = 3\) поэтому мы имеем слабый до, и мы будем принимать \(V = \frac{1}{\nu} I\) , который будет тянуть нашу оценку ковариационной к идентичности (напомним , что среднее значение \(\nu V\)).
PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF
def log_lik_prior_numpy(precision):
rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
return rv.logpdf(precision)
# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)
-9.103606346649766
Распределение Уишарта является сопряженным перед для оценки точности матрицы многомерных нормального с известным средним \(\mu\).
Предположим , что предыдущие параметры Уишарт являются \(\nu, V\) и что мы имеем \(n\) наблюдения нашего многомерного нормального, \(x_1, \ldots, x_n\). Задние параметры \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).
n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
(v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))
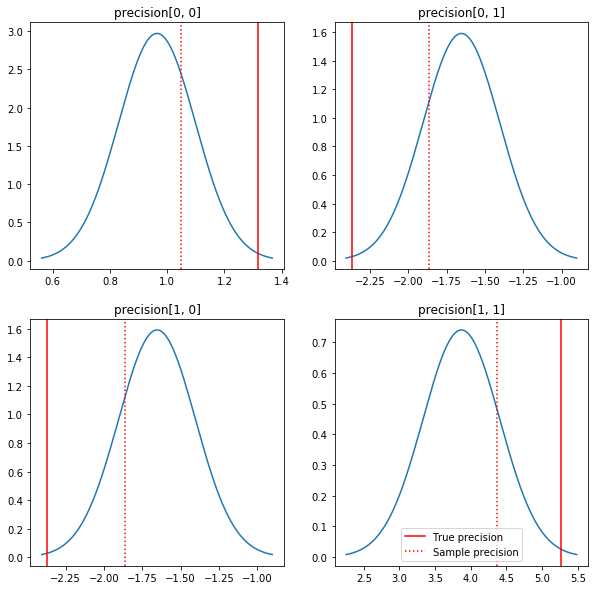
Быстрый сюжет апостериорства и истинных значений. Обратите внимание, что задние части близки к задним частям образца, но немного сужены в сторону идентичности. Также обратите внимание, что истинные значения довольно далеки от апостериорного режима - по-видимому, это связано с тем, что предыдущие значения не очень хорошо подходят для наших данных. В реальной проблеме мы бы скорее всего лучше с чем - то вроде уменьшенным обратной Wishart перед для ковариации (см, например, Эндрю Гельман комментарии на эту тему), но тогда мы бы не иметь хорошую аналитические кзади.
sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
for j in range(2):
ax = axes[i, j]
loc = posterior_mean[i, j]
scale = posterior_sd[i, j]
xmin = loc - 3.0 * scale
xmax = loc + 3.0 * scale
x = np.linspace(xmin, xmax, 1000)
y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
ax.plot(x, y)
ax.axvline(true_precision[i, j], color='red', label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()
Шаг 3. Реализуйте функцию правдоподобия в TensorFlow
Спойлер: Наша первая попытка не сработает; О том, почему, поговорим ниже.
Подсказка: используйте TensorFlow нетерпеливого режим при разработке ваших функций правдоподобия. Нетерпеливый режим делает вести себя TF больше как NumPy - все немедленно выполняется, так что вы можете отлаживать в интерактивном режиме, вместо того, чтобы использовать Session.run() . Смотрите примечания здесь .
Предварительно: классы распределения
TFP имеет набор классов распределения, которые мы будем использовать для генерации наших вероятностей журнала. Следует отметить, что эти классы работают с тензорами выборок, а не только с отдельными выборками - это позволяет осуществлять векторизацию и связанные с этим ускорения.
Распределение может работать с тензором выборок двумя разными способами. Проще всего проиллюстрировать эти два способа на конкретном примере, включающем распределение с одним скалярным параметром. Я буду использовать Пуассон распределение, которое имеет rate параметр.
- Если мы создадим Пуассона с одним значением для
rateпараметра, вызов егоsample()метод возвращает одно значение. Это значение называетсяevent, и в этом случае событие все скаляры. - Если мы создаем Пуассон с тензором значений для
rateпараметра, вызов егоsample()метода теперь возвращает несколько значений, по одному для каждого значения тензора скорости. Объект действует как совокупность независимых Poissons, каждый со своей собственной скоростью, и каждое из значений , возвращаемый вызовомsample()соответствует одному из этих Poissons. Эта коллекция независимых , но не одинаково распределенные событий называетсяbatch. -
sample()метод принимаетsample_shapeпараметр , который по умолчанию пустой кортеж. Переходя непустое значение дляsample_shapeрезультатов в выборке , вернувшихся несколько партий. Эта коллекция партий называетсяsample.
Распределение по log_prob() метод потребляет данные таким образом , чтобы параллели , как sample() генерирует его. log_prob() возвращает вероятности для образцов, т.е. для нескольких независимых партий событий.
- Если у нас есть объект Пуассон , который был создан с скалярной
rate, каждая партия является скаляром, и если мы перейдем в тензоре образцов, мы выберемся тензором того же размера журнала вероятностей. - Если у нас есть объект Пуассона , который был создан с тензором формы
Tотrateзначений, каждая партия представляет собой тензор формыT. Если мы передадим тензор выборок формы D, T, мы получим тензор логарифмических вероятностей формы D, T.
Ниже приведены несколько примеров, иллюстрирующих эти случаи. Смотрите этот ноутбук для более подробного учебника о событиях, партиях и формах.
# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))
# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters. Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))
print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())
iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385] draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]
Вероятность регистрации данных
Сначала мы реализуем функцию правдоподобия журнала данных.
VALIDATE_ARGS = True
ALLOW_NAN_STATS = False
Одним из ключевых отличий от случая NumPy является то, что наша функция правдоподобия TensorFlow должна будет обрабатывать векторы матриц точности, а не только отдельные матрицы. Векторы параметров будут использоваться при выборке из нескольких цепочек.
Мы создадим объект распределения, который работает с пакетом матриц точности (то есть по одной матрице на цепочку).
При вычислении вероятностей журнала наших данных нам потребуется, чтобы наши данные реплицировались таким же образом, как и наши параметры, чтобы на каждую переменную пакета была одна копия. Форма наших реплицированных данных должна быть следующей:
[sample shape, batch shape, event shape]
В нашем случае форма события равна 2 (поскольку мы работаем с двумерными гауссианами). Форма образца - 100, так как у нас 100 образцов. Форма пакета будет просто количеством матриц точности, с которыми мы работаем. Реплицировать данные каждый раз, когда мы вызываем функцию правдоподобия, расточительно, поэтому мы заранее реплицируем данные и передадим реплицированную версию.
Обратите внимание , что это неэффективная реализация: MultivariateNormalFullCovariance является дорогостоящим по сравнению с некоторыми альтернативами , которые мы будем говорить в разделе оптимизации в конце.
def log_lik_data(precisions, replicated_data):
n = tf.shape(precisions)[0] # number of precision matrices
# We're estimating a precision matrix; we have to invert to get log
# probabilities. Cholesky inversion should be relatively efficient,
# but as we'll see later, it's even better if we can avoid doing the Cholesky
# decomposition altogether.
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data). We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)
(100, 2, 2)
Совет: Одна вещь , которую я нашел , чтобы быть чрезвычайно полезным пишет мало вменяемости проверки моих функций TensorFlow. Очень легко испортить векторизацию в TF, поэтому наличие более простых функций NumPy - отличный способ проверить вывод TF. Думайте об этом как о небольших модульных тестах.
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
Вероятность предыдущего журнала
Предыдущее проще, поскольку нам не нужно беспокоиться о репликации данных.
@tf.function(autograph=False)
def log_lik_prior(precisions):
rv_precision = tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions)
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]))
print('tensorflow:', lik_tf[i])
0 numpy: -2.2351873809649625 tensorflow: -2.2351875 1 numpy: -9.103606346649766 tensorflow: -9.103608
Постройте функцию правдоподобия совместного журнала
Приведенная выше функция правдоподобия журнала данных зависит от наших наблюдений, но в сэмплере их не будет. Мы можем избавиться от зависимости без использования глобальной переменной с помощью [закрытия] (https://en.wikipedia.org/wiki/Closure_ (computer_programming)). Замыкания включают внешнюю функцию, которая создает среду, содержащую переменные, необходимые для внутренняя функция.
def get_log_lik(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik(precision):
return log_lik_data(precision, replicated_data) + log_lik_prior(precision)
return _log_lik
Шаг 4: образец
Хорошо, пора пробовать! Для простоты мы будем использовать только 1 цепочку, а в качестве отправной точки будем использовать единичную матрицу. Позже мы сделаем все более тщательно.
Опять же, это не сработает - мы получим исключение.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.expand_dims(tf.eye(2), axis=0)
# Use expand_dims because we want to pass in a tensor of starting values
log_lik_fn = get_log_lik(my_data, n_chains=1)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
return states
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
Cholesky decomposition was not successful. The input might not be valid.
[[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]
Function call stack:
sample
...
Function call stack:
sample
Выявление проблемы
InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. Это не очень полезно. Посмотрим, сможем ли мы узнать больше о том, что произошло.
- Мы распечатаем параметры для каждого шага, чтобы увидеть значение, при котором что-то не получается.
- Мы добавим несколько утверждений для защиты от конкретных проблем.
Утверждения сложны, потому что они являются операциями TensorFlow, и мы должны позаботиться о том, чтобы они выполнялись и не выходили за пределы графика. Это стоит прочитать этот обзор отладки TensorFlow , если вы не знакомы с утверждениями TF. Вы можете явно заставить утверждение выполнить с помощью tf.control_dependencies (см комментариев в коде ниже).
Родная TensorFlow в Print функция имеет такое же поведение , как утверждения - это операция, и вам нужно принять некоторые меры для обеспечения того , чтобы она выполняет. Print вызывает дополнительные головные боли , когда мы работаем в записной книжке: его вывод направляется в stderr , и stderr не отображается в ячейке. Мы будем использовать трюк здесь: вместо того , чтобы использовать tf.Print , мы создаем нашу собственную операцию TensorFlow печати через tf.pyfunc . Как и в случае с утверждениями, мы должны убедиться, что наш метод выполняется.
def get_log_lik_verbose(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
def _log_lik(precisions):
# An internal method we'll make into a TensorFlow operation via tf.py_func
def _print_precisions(precisions):
print('precisions:\n', precisions)
return False # operations must return something!
# Turn our method into a TensorFlow operation
print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)
# Assertions are also operations, and some care needs to be taken to ensure
# that they're executed
assert_op = tf.assert_equal(
precisions, tf.linalg.matrix_transpose(precisions),
message='not symmetrical', summarize=4, name='symmetry_check')
# The control_dependencies statement forces its arguments to be executed
# before subsequent operations
with tf.control_dependencies([print_op, assert_op]):
return (log_lik_data(precisions, replicated_data) +
log_lik_prior(precisions))
return _log_lik
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.eye(2)[tf.newaxis, ...]
log_lik_fn = get_log_lik_verbose(my_data)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[ 0.24315196 -0.2761638 ]
[-0.33882257 0.8622 ]]]
assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
[[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]
Function call stack:
sample
...
Function call stack:
sample
Почему это не удается
Самым первым новым значением параметра, которое пробует пробоотборник, является асимметричная матрица. Это приводит к сбою разложения Холецкого, поскольку оно определено только для симметричных (и положительно определенных) матриц.
Проблема здесь в том, что наш интересующий параметр представляет собой матрицу точности, а матрицы точности должны быть действительными, симметричными и положительно определенными. Сэмплер ничего не знает об этом ограничении (кроме, возможно, градиентов), поэтому вполне возможно, что сэмплер предложит недопустимое значение, что приведет к исключению, особенно если размер шага большой.
С гамильтоновым сэмплером Монте-Карло мы можем обойти проблему, используя очень маленький размер шага, поскольку градиент должен удерживать параметры вдали от недопустимых областей, но маленькие размеры шага означают медленную сходимость. С семплером Metropolis-Hastings, который ничего не знает о градиентах, мы обречены.
Версия 2: изменение параметров до неограниченных параметров
Существует простое решение проблемы, описанной выше: мы можем изменить параметры нашей модели так, чтобы новые параметры больше не имели этих ограничений. TFP предоставляет полезный набор инструментов - бижекторов - для этого.
Репараметризация бижекторами
Наша матрица точности должна быть реальной и симметричной; нам нужна альтернативная параметризация, не имеющая этих ограничений. Отправной точкой является факторизация Холецкого матрицы точности. Факторы Холецкого по-прежнему ограничены - они имеют нижний треугольник, а их диагональные элементы должны быть положительными. Однако, если мы возьмем логарифм диагоналей фактора Холецкого, то бревна больше не будут ограничены положительными значениями, а затем, если мы сгладим нижнюю треугольную часть в одномерный вектор, у нас больше не будет ограничения нижнего треугольника. . Результатом в нашем случае будет вектор длины 3 без ограничений.
(The ручной Стан имеет большой раздел об использовании преобразований для удаления различных типов ограничений на параметры.)
Эта повторная параметризация мало влияет на нашу функцию правдоподобия журнала данных - нам просто нужно инвертировать наше преобразование, чтобы мы вернули матрицу точности, - но влияние на предыдущее сложнее. Мы указали, что вероятность данной матрицы точности определяется распределением Уишарта; какова вероятность нашей преобразованной матрицы?
Напомним , что если мы применим монотонная функция \(g\) к 1-D случайная величина \(X\), \(Y = g(X)\), плотность для \(Y\) дается
\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]
Производная \(g^{-1}\) срока приходится так , что \(g\) локальных изменений объемов. Для получения более высокой размерности случайных величин, поправочный коэффициент является абсолютное значение определителя якобиану \(g^{-1}\) (см здесь ).
Нам придется добавить якобиан обратного преобразования в нашу логарифмическую функцию априорного правдоподобия. К счастью, TFP в Bijector класс может позаботиться об этом для нас.
Bijector класс используются для представления обратимых, гладкие функций , используемых для изменения переменных в функции плотности вероятности. Bijectors все имеют forward() метод , который выполняет преобразование, в inverse() метод , который переворачивает его, и forward_log_det_jacobian() и inverse_log_det_jacobian() методы , которые обеспечивают якобиевы корректировки нам нужно , когда мы reparaterize в формате PDF.
TFP предоставляет набор полезных bijectors , что мы можем объединить через композицию с помощью Chain оператора с образованием довольно сложных преобразований. В нашем случае составим следующие 3 бижектора (операции в цепочке выполняются справа налево):
- Первым шагом нашего преобразования является факторизация Холецкого матрицы точности. Для этого не существует класса Bijector; Однако
CholeskyOuterProductbijector принимает продукт 2 Холецких факторов. Мы можем использовать обратные эту операцию с помощьюInvertоператора. - Следующим шагом будет логарифм диагональных элементов фактора Холецкого. Мы достигаем этого с помощью
TransformDiagonalbijector и обратной величиныExpbijector. - Наконец , мы выравнивать нижнюю треугольную часть матрицы на вектор , используя инверсию
FillTriangularbijector.
# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
# step 3: flatten the lower triangular portion of the matrix
tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
# step 2: take the log of the diagonals
tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
# step 1: decompose the precision matrix into its Cholesky factors
tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])
# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)
# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)
print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()
print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())
single input: m: [[1. 2.] [2. 8.]] precision_to_unconstrained(m): [0.6931472 2. 0. ] inverse(precision_to_unconstrained(m)): [[1. 2.] [2. 8.]] tensor of inputs: m2: [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]] precision_to_unconstrained(m2): [[0.6931472 2. 0. ] [0. 0. 0. ]] inverse(precision_to_unconstrained(m2)): [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]]
TransformedDistribution класс автоматизирует процесс применения bijector к распределению и сделать необходимые поправки к якобиеву log_prob() . Наш новый приор становится:
def log_lik_prior_transformed(transformed_precisions):
rv_precision = tfd.TransformedDistribution(
tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS),
bijector=precision_to_unconstrained,
validate_args=VALIDATE_ARGS)
return rv_precision.log_prob(transformed_precisions)
# Check against the numpy implementation. Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow: -0.84889317 1 numpy: -7.305657151741624 tensorflow: -7.305659
Нам просто нужно инвертировать преобразование для вероятности нашего журнала данных:
precision = precision_to_unconstrained.inverse(transformed_precision)
Поскольку на самом деле нам нужна факторизация Холецкого матрицы точности, было бы более эффективно сделать здесь частичное обратное. Однако мы оставим оптимизацию на потом, а частичное обратное оставим читателю в качестве упражнения.
def log_lik_data_transformed(transformed_precisions, replicated_data):
# We recover the precision matrix by inverting our bijector. This is
# inefficient since we really want the Cholesky decomposition of the
# precision matrix, and the bijector has that in hand during the inversion,
# but we'll worry about efficiency later.
n = tf.shape(transformed_precisions)[0]
precisions = precision_to_unconstrained.inverse(transformed_precisions)
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
transformed_precisions, replicated_data).numpy()
for i in range(precisions.shape[0]):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
Снова мы завершаем наши новые функции закрытием.
def get_log_lik_transformed(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_transformed(transformed_precisions):
return (log_lik_data_transformed(transformed_precisions, replicated_data) +
log_lik_prior_transformed(transformed_precisions))
return _log_lik_transformed
# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)
[-431.5611]
Отбор проб
Теперь, когда нам не нужно беспокоиться о взрыве нашего сэмплера из-за недопустимых значений параметров, давайте сгенерируем несколько реальных сэмплов.
Сэмплер работает с неограниченной версией наших параметров, поэтому нам нужно преобразовать наше начальное значение в его неограниченную версию. Сэмплы, которые мы генерируем, также будут в неограниченной форме, поэтому нам нужно преобразовать их обратно. Бижекторы векторизованы, поэтому это легко сделать.
# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_value = initial_value_cholesky.dot(
initial_value_cholesky.T)[np.newaxis, ...]
# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
initial_value).numpy()
# Sample!
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)
num_results = 1000
num_burnin_steps = 1000
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
initial_value_transformed,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=lambda _, pkr: pkr.is_accepted,
seed=123)
# transform samples back to their constrained form
precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
Давайте сравним среднее значение выхода нашего пробоотборника с аналитическим апостериорным средним!
print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Sample mean: [[ 1.4315274 -0.25587553] [-0.25587553 0.5740424 ]]
Мы далеко! Разберемся почему. Сначала посмотрим на наши образцы.
np.reshape(precision_samples, [-1, 2, 2])
array([[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
...,
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]]], dtype=float32)
Ой, похоже, все они имеют одинаковую ценность. Разберемся почему.
kernel_results_ переменный именованный кортеж , который дает информацию о пробоотборнике в каждом штате. is_accepted поле является ключевым здесь.
# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))
[False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False] Fraction of samples accepted: 0.0
Все наши образцы были забракованы! Предположительно наш размер шага был слишком большим. Я выбрал stepsize=0.1 чисто произвольно.
Версия 3: выборка с адаптивным размером шага
Поскольку выборка с произвольным выбором размера шага не удалась, у нас есть несколько пунктов повестки дня:
- реализовать адаптивный размер шага и
- выполнить некоторые проверки сходимости.
Существует некоторый хороший пример кода в tensorflow_probability/python/mcmc/hmc.py для реализации адаптивных размеров шага. Я адаптировал его ниже.
Обратите внимание , что есть отдельный sess.run() заявление для каждого шага. Это действительно полезно для отладки, так как позволяет при необходимости легко добавлять пошаговую диагностику. Например, мы можем показать постепенный прогресс, время каждого шага и т. Д.
Совет: Один по- видимому , общий способ испортить ваш отбор проб должен иметь свой график расти в цикле. (Причина завершения графика перед запуском сеанса состоит в том, чтобы предотвратить именно такие проблемы.) Однако, если вы не использовали finalize (), полезная проверка отладки, если ваш код замедляется до обхода, - это распечатать график размер на каждом шаге через len(mygraph.get_operations()) - если длина увеличивается, вы , вероятно , делать что - то плохое.
Мы собираемся запустить здесь 3 независимых цепочки. Выполнение некоторых сравнений между цепочками поможет нам проверить сходимость.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values = []
for i in range(N_CHAINS):
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)
initial_values_transformed = precision_to_unconstrained.forward(
initial_values).numpy()
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=hmc,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values_transformed,
kernel=adapted_kernel,
trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
parallel_iterations=1)
# transform samples back to their constrained form
precision_samples = precision_to_unconstrained.inverse(states)
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
Быстрая проверка: наш показатель приемлемости во время выборки близок к нашему целевому значению 0,651.
print(np.mean(is_accepted))
0.6190666666666667
Более того, среднее значение нашей выборки и стандартное отклонение близки к тому, что мы ожидаем от аналитического решения.
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96426415 -1.6519215 ] [-1.6519215 3.8614824 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13622096 0.25235635] [0.25235635 0.5394968 ]]
Проверка сходимости
Как правило, у нас не будет аналитического решения для проверки, поэтому нам нужно убедиться, что сэмплер сошелся. Один стандартный чек является Гельман-Рубин \(\hat{R}\) статистики, которая требует нескольких цепочек выборки. \(\hat{R}\) измеряет степень , в которой дисперсия (средств) между цепями превышает то , что можно было бы ожидать , если бы цепи были одинаково распределены. Значения \(\hat{R}\) близких к 1 используются для обозначения приблизительной сходимости. Смотрите источник для деталей.
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0038308 1.0005717] [1.0005717 1.0006068]]
Модельная критика
Если бы у нас не было аналитического решения, пора было бы критиковать настоящую модель.
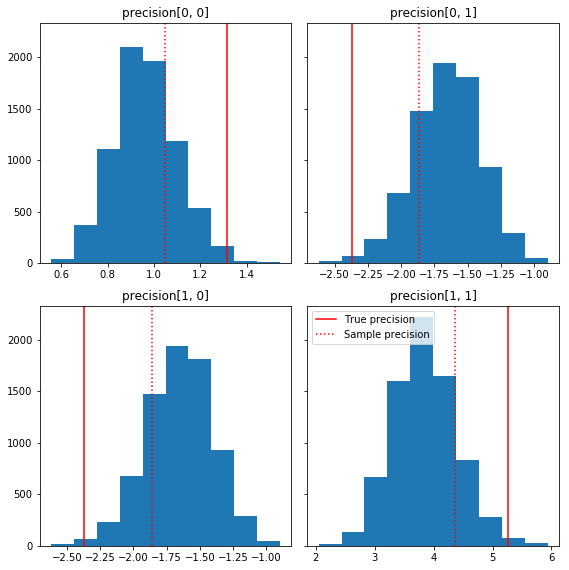
Вот несколько быстрых гистограмм компонентов выборки относительно нашей базовой истины (выделены красным). Обратите внимание, что выборки были сокращены от значений матрицы выборочной точности до единичной матрицы ранее.
fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
for j in range(2):
ax = axes[i, j]
ax.hist(precision_samples_reshaped[:, i, j])
ax.axvline(true_precision[i, j], color='red',
label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':',
label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()
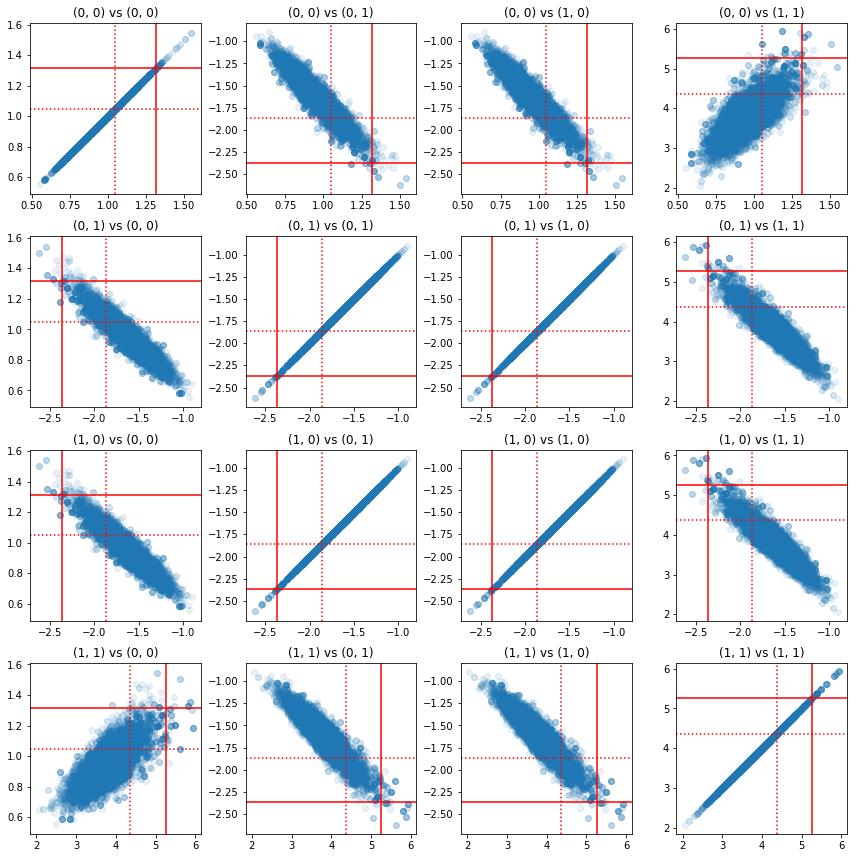
Некоторые диаграммы разброса пар компонентов точности показывают, что из-за корреляционной структуры апостериорных значений истинные апостериорные значения не так маловероятны, как они выглядят из маргиналов выше.
fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
for j1 in range(2):
index1 = 2 * i1 + j1
for i2 in range(2):
for j2 in range(2):
index2 = 2 * i2 + j2
ax = axes[index1, index2]
ax.scatter(precision_samples_reshaped[:, i1, j1],
precision_samples_reshaped[:, i2, j2], alpha=0.1)
ax.axvline(true_precision[i1, j1], color='red')
ax.axhline(true_precision[i2, j2], color='red')
ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()
Версия 4: более простая выборка ограниченных параметров
Бижекторы упростили выборку прецизионной матрицы, но потребовалось изрядное количество ручных преобразований в неограниченное представление и обратно. Есть способ попроще!
Ядро TransformedTransition
TransformedTransitionKernel упрощает этот процесс. Он обертывает ваш сэмплер и обрабатывает все преобразования. Он принимает в качестве аргумента список бижекторов, которые сопоставляют неограниченные значения параметров с ограниченными. Поэтому здесь нам нужно обратное precision_to_unconstrained bijector мы использовали выше. Мы могли бы просто использовать tfb.Invert(precision_to_unconstrained) , но это будет включать в себя взятие обратных обратных (TensorFlow не достаточно умен , чтобы упростить tf.Invert(tf.Invert()) в tf.Identity()) , так что вместо этого мы Так же напишу новый бижектор.
Сдерживающий биектор
# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
# step 3: take the product of Cholesky factors
tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: map a vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()
print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)
m: [[1.0, 2.0], [2.0, 8.0]] unconstrained_to_precision.inverse(m): [0.6931472 2. 0. ] forward(unconstrained_to_precision.inverse(m)): [[1. 2.] [2. 8.]]
Выборка с помощью TransformedTransitionKernel
С TransformedTransitionKernel , мы больше не придется делать вручную преобразования наших параметров. Наши начальные значения и наши образцы - все матрицы точности; нам просто нужно передать наш неограниченный бижектор (-ы) ядру, и оно позаботится обо всех преобразованиях.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
return states
precision_samples = sample()
Проверка сходимости
\(\hat{R}\) проверки сходимости выглядит хорошо!
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013582 1.0019467] [1.0019467 1.0011805]]
Сравнение с аналитическим апостериорным
Снова проверим с аналитическим апостериорным.
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96687526 -1.6552585 ] [-1.6552585 3.867676 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329624 0.24913791] [0.24913791 0.53983927]]
Оптимизация
Теперь, когда у нас есть сквозная работа, давайте сделаем более оптимизированную версию. Скорость не имеет большого значения для этого примера, но как только матрицы станут больше, несколько оптимизаций будут иметь большое значение.
Одно большое улучшение скорости, которое мы можем сделать, - это изменить параметры в терминах разложения Холецкого. Причина в том, что для нашей функции правдоподобия данных требуются как ковариационная, так и прецизионная матрицы. Матрица инверсия дорого (\(O(n^3)\) для \(n \times n\) матрицы), и если мы параметризация в терминах либо ковариации или прецизионной матрице, нам нужно сделать инверсию , чтобы получить другие.
В качестве напоминания, реальная, положительно определенная, симметричная матрица \(M\) можно разложить в произведение вида \(M = L L^T\) где матрица \(L\) является нижней треугольной и имеет положительные диагонали. Учитывая , разложение Холецкого из \(M\), можно более эффективно получить как \(M\) (продукт низшей и верхнюю матрицу треугольной формы) и \(M^{-1}\) (через обратной подстановки). Сама по себе факторизация Холецкого обходится недешево, но если мы параметризуем в терминах факторов Холецкого, нам нужно только вычислить факторизацию Холексы для начальных значений параметров.
Использование разложения Холецкого ковариационной матрицы
TFP имеет версию многомерного нормального распределения, MultivariateNormalTriL , что спараметрированное с точкой зрения коэффициента Холесского ковариационной матрицы. Таким образом, если бы мы параметризовали ковариационную матрицу с помощью коэффициента Холецкого, мы могли бы эффективно вычислить логарифмическое правдоподобие. Проблема состоит в том, чтобы вычислить априорную логарифмическую вероятность с аналогичной эффективностью.
Если бы у нас была версия обратного распределения Вишарта, которая работала бы с факторами Холецкого выборок, все было бы готово. Увы, нет. (Однако команда приветствовала бы отправку кода!) В качестве альтернативы мы можем использовать версию дистрибутива Wishart, которая работает с факторами Холецкого образцов вместе с цепочкой бижекторов.
На данный момент нам не хватает нескольких стандартных бижекторов, чтобы сделать вещи действительно эффективными, но я хочу показать процесс как упражнение и полезную иллюстрацию силы бижекторов TFP.
Распределение Уишарта, работающее на факторах Холецкого
Wishart распределение имеет полезный флаг, input_output_cholesky , что указывает , что входные и выходные матрицы должны быть Холецкого факторы. Работать с факторами Холецкого более эффективно и численно выгоднее, чем с полными матрицами, поэтому это желательно. Важное замечание по поводу семантики флага: это только свидетельствует о том , что представление на входе и выходе на распределение должно измениться - это не означает полный Репараметризационно распределения, которая будет включать якобиеву поправку к log_prob() функция. На самом деле мы хотим полностью изменить параметры, поэтому создадим собственный дистрибутив.
# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices. Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).
class CholeskyWishart(tfd.TransformedDistribution):
"""Wishart distribution reparameterized to use Cholesky factors."""
def __init__(self,
df,
scale_tril,
validate_args=False,
allow_nan_stats=True,
name='CholeskyWishart'):
# Wishart has a bunch of methods that we want to support but not
# implement. We'll subclass TransformedDistribution here to take care of
# those. We'll override the few for which speed is critical and implement
# them with a separate Wishart for which input_output_cholesky=True
super(CholeskyWishart, self).__init__(
distribution=tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=False,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
validate_args=validate_args,
name=name
)
# Here's the Cholesky distribution we'll use for log_prob() and sample()
self.cholesky = tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=True,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats)
def _log_prob(self, x):
return (self.cholesky.log_prob(x) +
self.bijector.inverse_log_det_jacobian(x, event_ndims=2))
def _sample_n(self, n, seed=None):
return self.cholesky._sample_n(n, seed)
# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
@tf.function(autograph=False)
def compute_log_prob(m):
w_transformed = tfd.TransformedDistribution(
tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
w_optimized = CholeskyWishart(
df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
log_prob_transformed = w_transformed.log_prob(m)
log_prob_optimized = w_optimized.log_prob(m)
return log_prob_transformed, log_prob_optimized
for matrix in [np.eye(2, dtype=np.float32),
np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
log_prob_transformed, log_prob_optimized = [
t.numpy() for t in compute_log_prob(matrix)]
print('Transformed Wishart:', log_prob_transformed)
print('Optimized Wishart', log_prob_optimized)
Transformed Wishart: -0.84889317 Optimized Wishart -0.84889317 Transformed Wishart: -99.269455 Optimized Wishart -99.269455
Построение обратного распределения Вишарта
У нас есть ковариационная матрица \(C\) разложен на \(C = L L^T\) где \(L\) является нижним треугольным и имеет положительную диагональ. Мы хотим знать вероятность \(L\) , учитывая , что \(C \sim W^{-1}(\nu, V)\) где \(W^{-1}\) является обратным распределением Уишарта.
Обратное распределение Wishart обладает свойством , что если \(C \sim W^{-1}(\nu, V)\), то точность матрицы \(C^{-1} \sim W(\nu, V^{-1})\). Таким образом , мы можем получить вероятность \(L\) через TransformedDistribution , который принимает в качестве параметров распределения Уишарт и bijector , который отображает коэффициент Чолески прецизионной матрицы к фактору Холесского его обратного.
Прямолинейный (но не супер эффективный) способ получить от фактора Холесского из \(C^{-1}\) к \(L\) является инвертировать фактор Чолески путем обратного решением, то формирование ковариационной матрицы из этих перевернутых факторов, а затем делать факторизацию Холецкой .
Пусть разложение Холецкого \(C^{-1} = M M^T\). \(M\) является нижней треугольной, так что мы можем перевернуть его с помощью MatrixInverseTriL bijector.
Формирование \(C\) из \(M^{-1}\) немного сложнее: \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) является нижней треугольной, так что \(M^{-1}\) также будет нижней треугольной и \(M^{-T}\) будет верхней треугольной. CholeskyOuterProduct() bijector работает только с нижними треугольными матрицами, поэтому мы не можем использовать его для формирования \(C\) от \(M^{-T}\). Наше обходное решение - это цепочка биекторов, которые переставляют строки и столбцы матрицы.
К счастью , эта логика заключена в CholeskyToInvCholesky bijector!
Объединение всех частей
# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()
print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)
numpy = [[ 1.0307764 0. ] [-0.03031695 0.12126781]] bijector = [[ 1.0307764 0. ] [-0.03031695 0.12126781]]
Наш финальный дистрибутив
Наша инверсия Уишарта, оперирующая факторами Холецкого, выглядит следующим образом:
inverse_wishart_cholesky = tfd.TransformedDistribution(
distribution=CholeskyWishart(
df=PRIOR_DF,
scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
bijector=tfb.CholeskyToInvCholesky())
У нас есть обратный Wishart, но он немного медленный, потому что нам нужно выполнить разложение Холецкого в биекторе. Вернемся к параметризации матрицы точности и посмотрим, что мы можем там сделать для оптимизации.
Финальная (!) Версия: использование разложения Холецкого матрицы точности
Альтернативный подход - работа с коэффициентами Холецкого матрицы точности. Здесь априорную функцию правдоподобия легко вычислить, но функция правдоподобия журнала данных требует больше работы, поскольку TFP не имеет версии многомерной нормали, параметризованной по точности.
Оптимизированная вероятность предыдущего журнала
Мы используем CholeskyWishart распределение мы построили выше построить предшествующее.
# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
def log_lik_prior_cholesky(precisions_cholesky):
rv_precision = CholeskyWishart(
df=PRIOR_DF,
scale_tril=PRIOR_SCALE_CHOLESKY,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions_cholesky)
# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
distribution=tfd.WishartTriL(
df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow slow:', lik_tf_slow[i])
print('tensorflow fast:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow slow: -0.84889317 tensorflow fast: -0.84889317 1 numpy: -7.442875031036973 tensorflow slow: -7.442877 tensorflow fast: -7.442876
Optimized data log likelihood
We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:
Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)
Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)
Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.
Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now
\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)
So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).
Our approach (courtesy of this notebook ):
- Use
tfd.Independent()to combine a batch of 1-DNormalrandom variables into a single multi-dimensional random variable. Thereinterpreted_batch_ndimsparameter forIndependent()specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, soreinterpreted_batch_ndims=1. - Apply a bijector to add the desired covariance:
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)). Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). Thetfb.Inverttakes care of inverting \(B\), and theadjoint=Trueflag performs the transpose. - Apply a bijector to add the desired offset:
tfb.Shift(shift=shift)Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).
class MVNPrecisionCholesky(tfd.TransformedDistribution):
"""Multivariate normal parameterized by loc and Cholesky precision matrix."""
def __init__(self, loc, precision_cholesky, name=None):
super(MVNPrecisionCholesky, self).__init__(
distribution=tfd.Independent(
tfd.Normal(loc=tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
adjoint=True)),
]),
name=name)
@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
n = tf.shape(precisions_cholesky)[0] # number of precision matrices
rv_data = MVNPrecisionCholesky(
loc=tf.zeros([n, 2]),
precision_cholesky=precisions_cholesky)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.81824
Combined log likelihood function
Now we combine our prior and data log likelihood functions in a closure.
def get_log_lik_cholesky(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_cholesky(precisions_cholesky):
return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
log_lik_prior_cholesky(precisions_cholesky))
return _log_lik_cholesky
Constraining bijector
Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.
unconstrained_to_precision_cholesky = tfb.Chain([
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: expand the vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)
precisions_cholesky: [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]] inv: [[ 0.0000000e+00 0.0000000e+00 0.0000000e+00] [ 3.5762781e-07 -2.0647411e+00 1.3721828e-01]] fwd(inv): [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]]
Initial values
We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values_cholesky = []
for i in range(N_CHAINS):
initial_values_cholesky.append(np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)
Sampling
We sample N_CHAINS chains using the TransformedTransitionKernel .
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_cholesky(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
samples = tf.linalg.matmul(states, states, transpose_b=True)
return samples
precision_samples = sample()
Convergence check
A quick convergence check looks good:
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013583 1.0019467] [1.0019467 1.0011804]]
Comparing results to the analytic posterior
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])
And again, the sample means and standard deviations match those of the analytic posterior.
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.9668749 -1.6552604] [-1.6552604 3.8676758]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329637 0.24913797] [0.24913797 0.53983945]]
Ok, all done! We've got our optimized sampler working.
