Ajustando modelos lineares generalizados de efeitos mistos usando inferência variacional

Instalar

Alternar código

TF_Installation = 'System'

if TF_Installation == 'TF Nightly':
  !pip install -q --upgrade tf-nightly
  print('Installation of `tf-nightly` complete.')
elif TF_Installation == 'TF Stable':
  !pip install -q --upgrade tensorflow
  print('Installation of `tensorflow` complete.')
elif TF_Installation == 'System':
  pass
else:
  raise ValueError('Selection Error: Please select a valid '
                   'installation option.')

Instalar

Alternar código

TFP_Installation = "System"

if TFP_Installation == "Nightly":
  !pip install -q tfp-nightly
  print("Installation of `tfp-nightly` complete.")
elif TFP_Installation == "Stable":
  !pip install -q --upgrade tensorflow-probability
  print("Installation of `tensorflow-probability` complete.")
elif TFP_Installation == "System":
  pass
else:
  raise ValueError("Selection Error: Please select a valid "
                   "installation option.")

Resumo

Neste colab, demonstramos como ajustar um modelo linear generalizado de efeitos mistos usando inferência variacional na Probabilidade do TensorFlow.

Família modelo

Lineares Generalizados modelos com efeito misto (MLG) são semelhantes aos linear generalizado modelos (GLM), excepto que eles incorporam um ruído amostra específica na resposta linear previsto. Isso é útil em parte porque permite que recursos raramente vistos compartilhem informações com recursos vistos mais comumente.

Como um processo generativo, um modelo linear generalizado de efeitos mistos (GLMM) é caracterizado por:

\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]

Onde:

\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]

Em outras palavras, este diz que cada categoria de cada grupo está associado a uma amostra, \(\beta_{rc}\), a partir de uma normal multivariada. Embora o \(\beta_{rc}\) atrai sempre são independentes, eles só são indentically distribuída para um grupo \(r\): aviso há exatamente um \(\Sigma_r\) para cada \(r\in\{1,\ldots,R\}\).

Quando affinely combinado com características de grupo de uma amostra (\(z_{r,i}\)), o resultado é o ruído específica amostra no \(i\)-ésimo previu resposta linear (que é de outro modo \(x_i^\top\omega\)).

Quando estimamos \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) estamos estimando essencialmente a quantidade de ruído de um grupo de efeito aleatório transporta que, caso contrário abafar o sinal presente na \(x_i^\top\omega\).

Há uma variedade de opções para o \(\text{Distribution}\) e função de ligação inversa , \(g^{-1}\). As escolhas comuns são:

• \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
• \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), e,
• \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).

Para mais possibilidades, ver a tfp.glm módulo.

Inferência Variacional

Infelizmente, encontrar as estimativas de máxima verossimilhança dos parâmetros \(\beta,\{\Sigma_r\}_r^R\) implica um integrante não-analítica. Para contornar esse problema, em vez disso,

1. Definir uma família com parâmetros de distribuição (o "substituto densidade"), denotado \(q_{\lambda}\) no apêndice.
2. Encontrar parâmetros \(\lambda\) para que \(q_{\lambda}\) está perto de nossa verdadeira denstiy alvo.

A família de distribuições será gaussianas independentes das dimensões adequadas, e por "perto de nossa densidade alvo", vamos significam "minimizar a divergência Kullback-Leibler ". Veja, por exemplo Secção de 2,2 "Variational Inference: Uma revisão para os estatísticos" para uma derivação bem escrito e motivação. Em particular, mostra que minimizar a divergência KL é equivalente a minimizar o limite inferior de evidência negativa (ELBO).

Problema de brinquedo

De Gelman et al. (2007) "conjunto de dados radon" é um conjunto de dados, por vezes usado para demonstrar abordagens para a regressão. (Por exemplo, esta intimamente relacionado pós PyMC3 blogue .) O conjunto de dados radon contém medidas internas de Radon tomadas em todo os Estados Unidos. Rádon é naturalmente ocorrentes gás radioactivo que é tóxico em concentrações elevadas.

Para nossa demonstração, vamos supor que estejamos interessados ​​em validar a hipótese de que os níveis de Radon são mais elevados em residências com porão. Também suspeitamos que a concentração de radônio está relacionada ao tipo de solo, ou seja, questões geográficas.

Para enquadrar isso como um problema de ML, tentaremos prever os níveis de log-radônio com base em uma função linear do piso em que a leitura foi feita. Também usaremos o condado como um efeito aleatório e, ao fazer isso, consideraremos as variações devido à geografia. Em outras palavras, vamos usar um modelo de efeito misto linear generalizado .

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import os
from six.moves import urllib

import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

Também faremos uma verificação rápida da disponibilidade de uma GPU:

if tf.test.gpu_device_name() != '/device:GPU:0':
  print("We'll just use the CPU for this run.")
else:
  print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))

We'll just use the CPU for this run.

Obtenha o conjunto de dados:

Carregamos o conjunto de dados do TensorFlow e fazemos um pré-processamento leve.

def load_and_preprocess_radon_dataset(state='MN'):
  """Load the Radon dataset from TensorFlow Datasets and preprocess it.

  Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
  to Minnesota data and preprocess to obtain the following features:
  - `county`: Name of county in which the measurement was taken.
  - `floor`: Floor of house (0 for basement, 1 for first floor) on which the
    measurement was taken.

  The target variable is `log_radon`, the log of the Radon measurement in the
  house.
  """
  ds = tfds.load('radon', split='train')
  radon_data = tfds.as_dataframe(ds)
  radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
  df = radon_data[radon_data.state==state.encode()].copy()

  df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
  # Make county names look nice. 
  df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
  # Remap categories to start from 0 and end at max(category).
  df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
  df['county_code'] = df.county.cat.codes
  # Radon levels are all positive, but log levels are unconstrained
  df['log_radon'] = df['radon'].apply(np.log)

  # Drop columns we won't use and tidy the index 
  columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
  df = df[columns_to_keep].reset_index(drop=True)

  return df

df = load_and_preprocess_radon_dataset()
df.head()

Especializando a Família GLMM

Nesta seção, especializamos a família GLMM para a tarefa de prever os níveis de radônio. Para fazer isso, primeiro consideramos o caso especial de efeito fixo de um GLMM:

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]

Este modelo pressupõe que o radônio log na observação \(j\) é (na expectativa) regidas pelo chão da \(j\)ª leitura é feita em, além de alguns interceptar constante. Em pseudocódigo, podemos escrever

def estimate_log_radon(floor):
    return intercept + floor_effect[floor]

há um peso aprendeu para cada andar e um universal intercept prazo. Olhando para as medições de radônio dos andares 0 e 1, parece que isso pode ser um bom começo:

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')

df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");

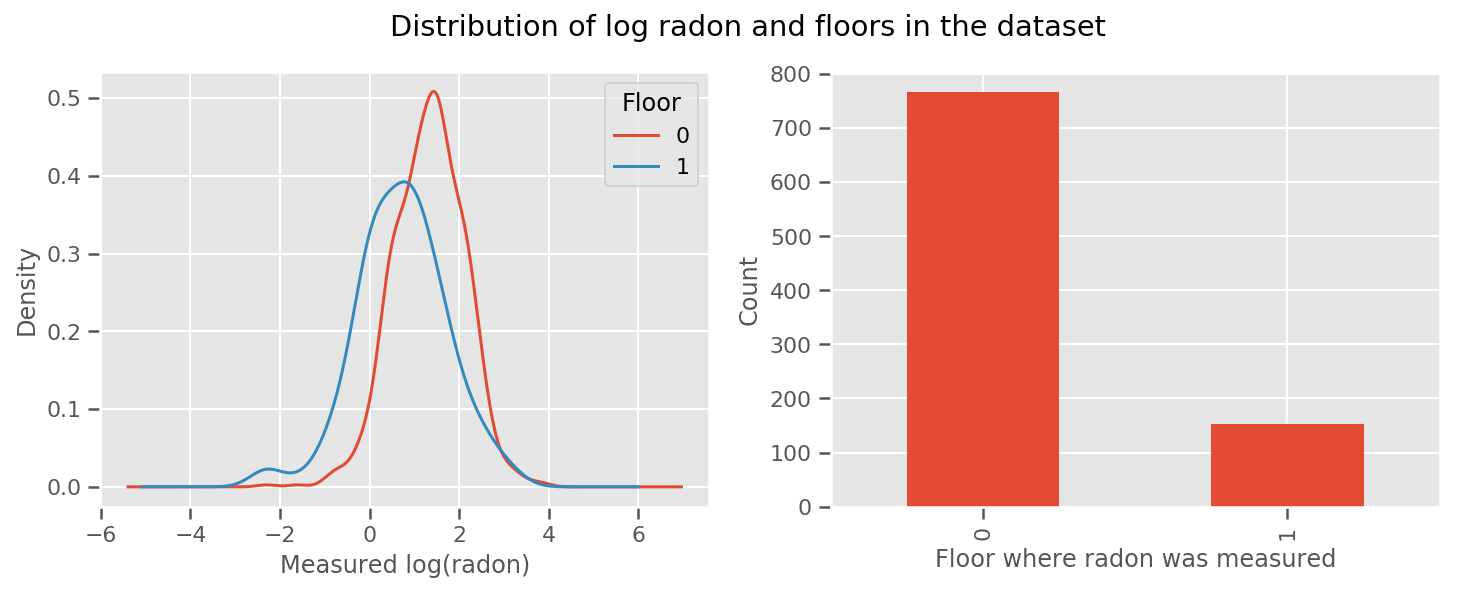
Tornar o modelo um pouco mais sofisticado, incluindo algo sobre geografia, é provavelmente ainda melhor: o radônio é parte da cadeia de decomposição do urânio, que pode estar presente no solo, então a geografia parece ser a chave para explicar.

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]

Novamente, em pseudocódigo, temos

def estimate_log_radon(floor, county):
    return intercept + floor_effect[floor] + county_effect[county]

o mesmo que antes, exceto com um peso específico do condado.

Dado um conjunto de treinamento suficientemente grande, este é um modelo razoável. No entanto, dados nossos dados de Minnesota, vemos que há um grande número de condados com um pequeno número de medições. Por exemplo, 39 de 85 condados têm menos de cinco observações.

Isso motiva o compartilhamento de força estatística entre todas as nossas observações, de uma forma que converge para o modelo acima conforme o número de observações por município aumenta.

fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');

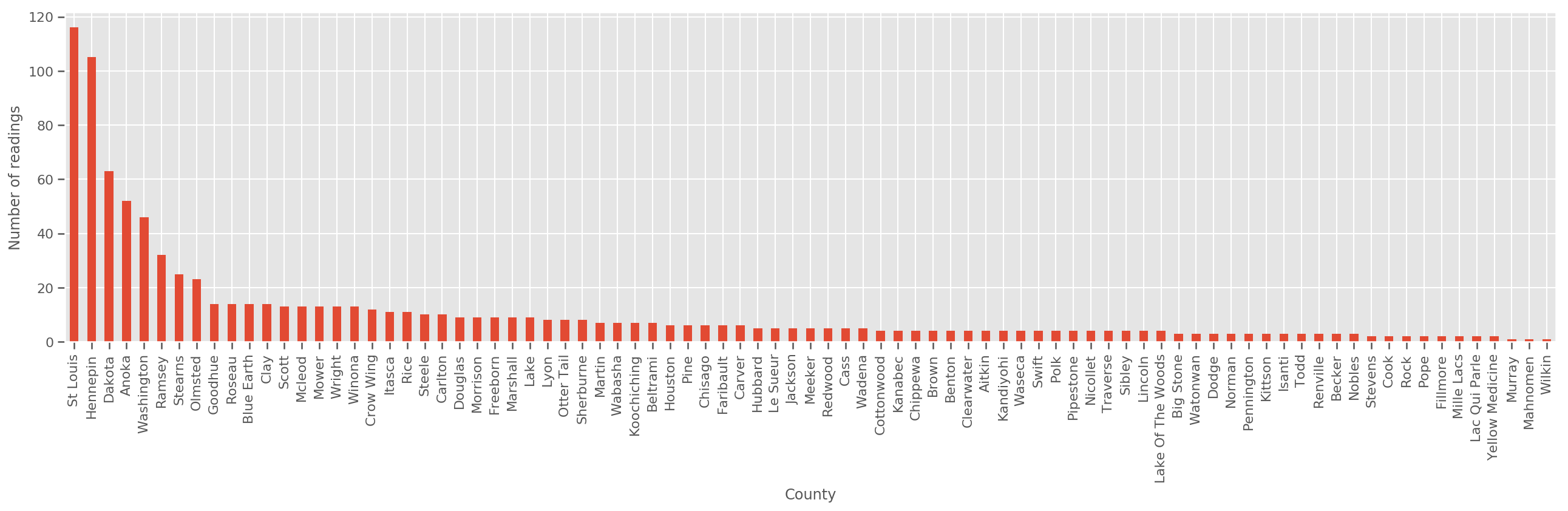
Se encaixam nesse modelo, o county_effect vector provavelmente acabar memorizando os resultados para municípios que tiveram apenas algumas amostras de treinamento, talvez overfitting e levando a pobre generalização.

O GLMM oferece um meio-termo feliz para os dois GLMs acima. Podemos considerar a adequação

\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]

Este modelo é o mesmo que o primeiro, mas temos posto a nossa probabilidade de ser uma distribuição normal, e irá partilhar a variância em todos os municípios através do (single) variável county_scale . Em pseudocódigo,

def estimate_log_radon(floor, county):
    county_mean = county_effect[county]
    random_effect = np.random.normal() * county_scale + county_mean
    return intercept + floor_effect[floor] + random_effect

Vamos inferir a distribuição conjunta sobre county_scale , county_mean , eo random_effect usando nossos dados observados. O mundial county_scale nos permite compartilhar a força estatística através municípios: aqueles com muitas observações fornecem um hit na variância de municípios com algumas observações. Além disso, conforme coletamos mais dados, este modelo convergirá para o modelo sem uma variável de escala combinada - mesmo com este conjunto de dados, chegaremos a conclusões semelhantes sobre os condados mais observados com qualquer um dos modelos.

Experimentar

Agora, tentaremos ajustar o GLMM acima usando inferência variacional no TensorFlow. Primeiro, dividiremos os dados em recursos e rótulos.

features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()

Especifique o modelo

def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):

  def model():
    county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
    intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
    floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
    county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
                                    scale=county_scale,
                                    name='county_prior')
    random_effect = tf.gather(county_prior, county, axis=-1)

    fixed_effect = intercept + floor_weight * floor
    linear_response = fixed_effect + random_effect
    yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
  return tfd.JointDistributionCoroutineAutoBatched(model)

joint = make_joint_distribution_coroutine(
    features.floor.values, features.county_code.values, df.county.nunique(),
    df.floor.nunique())

# Define a closure over the joint distribution 
# to condition on the observed labels.
def target_log_prob_fn(*args):
  return joint.log_prob(*args, likelihood=labels)

Especifique o posterior substituto

Vamos agora montar uma família substituta \(q_{\lambda}\), onde os parâmetros \(\lambda\) são treináveis. Neste caso, a nossa família é distribuições independentes multivariados normais, uma para cada parâmetro, e \(\lambda = \{(\mu_j, \sigma_j)\}\), quando \(j\) indexa os quatro parâmetros.

O método que usamos para ajustar os substitutos usos família tf.Variables . Nós também usamos tfp.util.TransformedVariable juntamente com Softplus para restringir os parâmetros (treinável) escala a ser positivo. Além disso, aplicamos Softplus a toda a scale_prior , que é um parâmetro positivo.

Inicializamos essas variáveis ​​treináveis ​​com um pouco de jitter para ajudar na otimização.

# Initialize locations and scales randomly with `tf.Variable`s and 
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
    tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
    initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
    bijector=tfb.Softplus())
n_counties = df.county.nunique()

surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
  tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())),           # scale_prior
  tfd.Normal(_init_loc(), _init_scale()),                           # intercept
  tfd.Normal(_init_loc(), _init_scale()),                           # floor_weight
  tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))])  # county_prior

Note-se que esta célula pode ser substituído por tfp.experimental.vi.build_factored_surrogate_posterior , como em:

surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
  event_shape=joint.event_shape_tensor()[:-1],
  constraining_bijectors=[tfb.Softplus(), None, None, None])

Resultados

Lembre-se de que nosso objetivo é definir uma família de distribuições parametrizadas tratáveis ​​e, em seguida, selecionar parâmetros para que tenhamos uma distribuição tratável próxima de nossa distribuição alvo.

Nós construímos a distribuição substituto acima, e pode usar tfp.vi.fit_surrogate_posterior , que aceita um otimizador e um determinado número de passos para encontrar os parâmetros para o modelo substituto minimizando o ELBO negativo (que está atribuído minimizar a divergência Kullback-Liebler entre o substituto e a distribuição de destino).

O valor de retorno é o ELBO negativo a cada passo, e as distribuições em surrogate_posterior terá sido atualizado com os parâmetros encontrados pelo otimizador.

optimizer = tf.optimizers.Adam(learning_rate=1e-2)

losses = tfp.vi.fit_surrogate_posterior(
    target_log_prob_fn, 
    surrogate_posterior,
    optimizer=optimizer,
    num_steps=3000, 
    seed=42,
    sample_size=2)

(scale_prior_, 
 intercept_, 
 floor_weight_, 
 county_weights_), _ = surrogate_posterior.sample_distributions()

print('        intercept (mean): ', intercept_.mean())
print('     floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))

intercept (mean):  tf.Tensor(1.4352839, shape=(), dtype=float32)
     floor_weight (mean):  tf.Tensor(-0.6701997, shape=(), dtype=float32)
 scale_prior (approx. mean):  tf.Tensor(0.28682157, shape=(), dtype=float32)

fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
       ylabel="Loss (ELBO)",
       title="Loss during training",
       ylim=0);

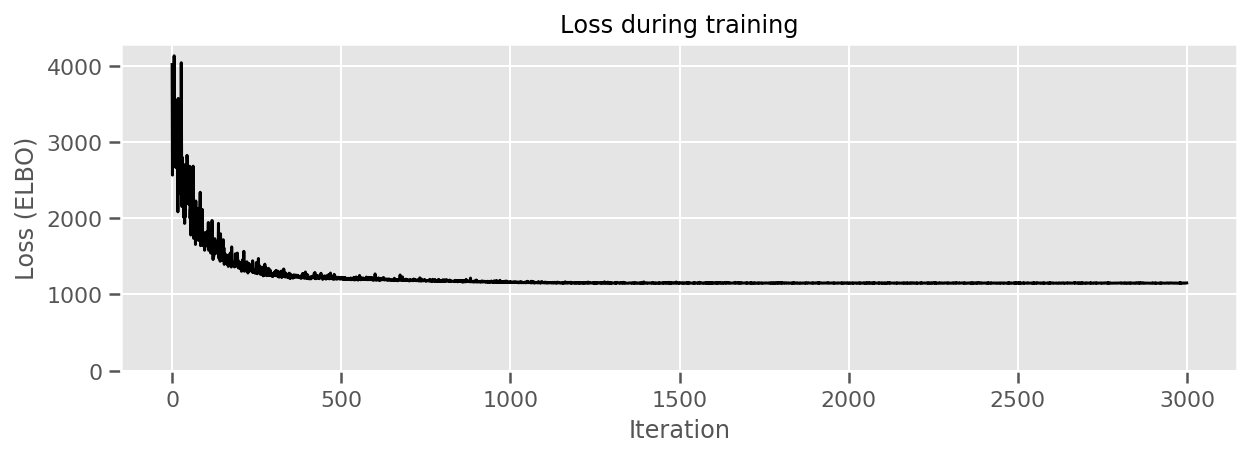
Podemos representar graficamente os efeitos médios estimados do condado, juntamente com a incerteza dessa média. Ordenamos isso por número de observações, com a maior à esquerda. Observe que a incerteza é pequena para os condados com muitas observações, mas é maior para os condados que têm apenas uma ou duas observações.

county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
                   .agg('size')
                   .sort_values(ascending=False)
                   .reset_index(name='count'))

means = county_weights_.mean()
stds = county_weights_.stddev()

fig, ax = plt.subplots(figsize=(20, 5))

for idx, row in county_counts.iterrows():
  mid = means[row.county_code]
  std = stds[row.county_code]
  ax.vlines(idx, mid - std, mid + std, linewidth=3)
  ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)

ax.set(
    xticks=np.arange(len(county_counts)),
    xlim=(-1, len(county_counts)),
    ylabel="County effect",
    title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);

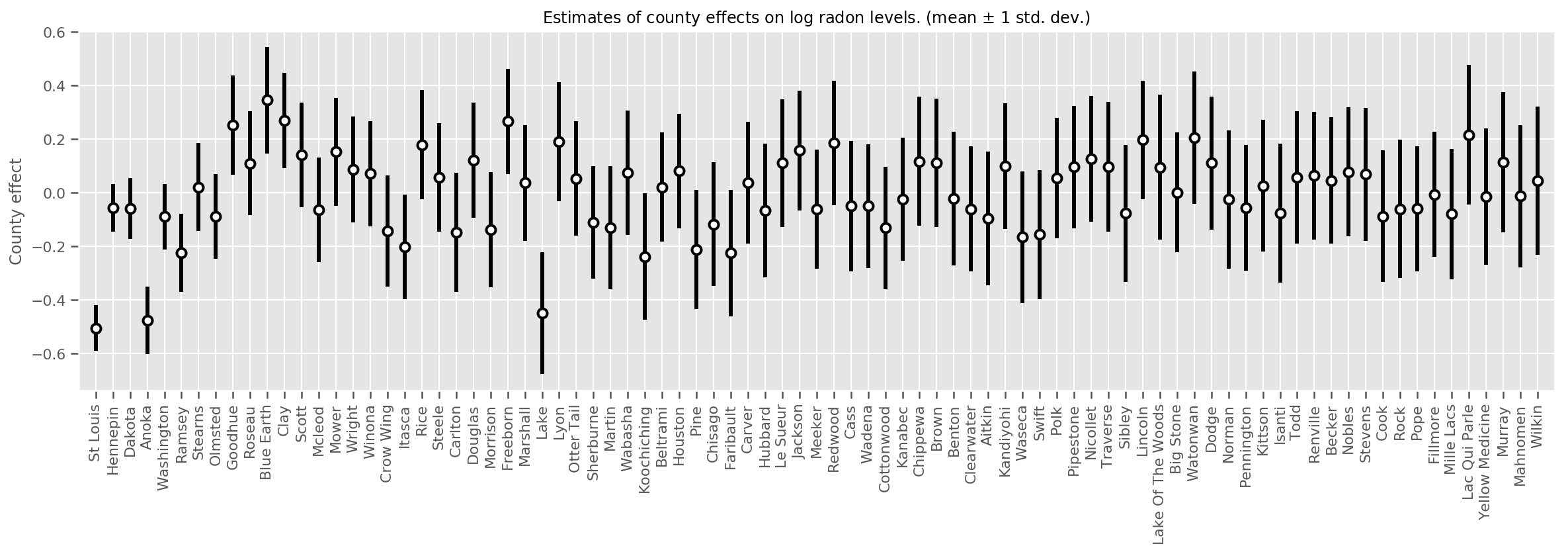
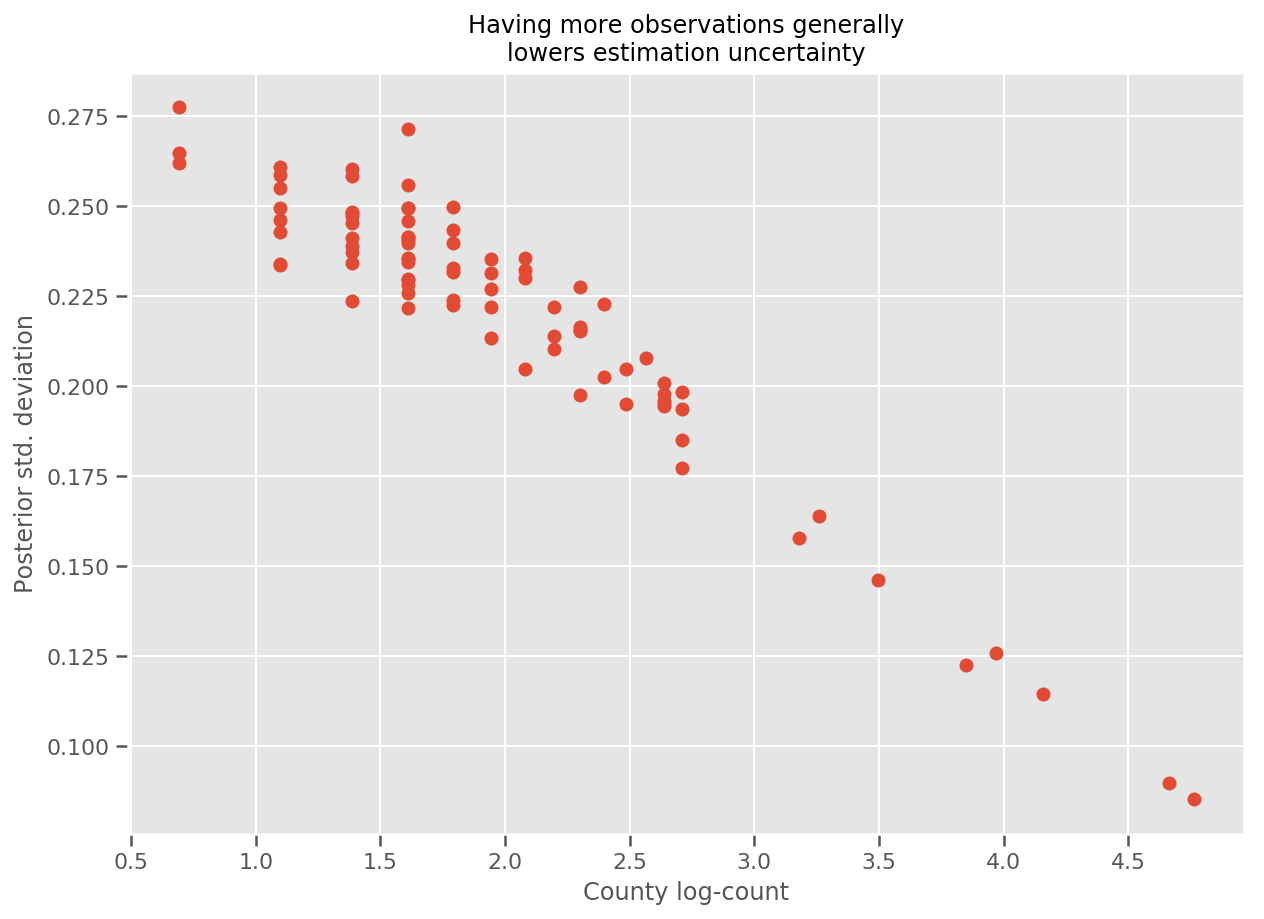
Na verdade, podemos ver isso mais diretamente traçando o log-número de observações contra o desvio padrão estimado e ver que a relação é aproximadamente linear.

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
    ylabel='Posterior std. deviation',
    xlabel='County log-count',
    title='Having more observations generally\nlowers estimation uncertainty'
);

Comparando a lme4 em R

%%shell
exit  # Trick to make this block not execute.

radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)

# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit

# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
#    Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
#  Groups   Name        Std.Dev.
#  county   (Intercept) 0.3282
#  Residual             0.7556
# Number of obs: 919, groups:  county, 85
# Fixed Effects:
# (Intercept)        floor
#       1.462       -0.693

<IPython.core.display.Javascript at 0x7f90b888e9b0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90bce1dfd0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>

A tabela a seguir resume os resultados.

print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
                             floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
                             scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
                   index=['lme4', 'vi']))

intercept   floor     scale
lme4   1.462000 -0.6930  0.328200
vi     1.435284 -0.6702  0.287251

Esta tabela indica os resultados estão dentro de VI ~ 10% de lme4 's. Isso é um tanto surpreendente, pois:

• lme4 é baseado no método de Laplace (não VI),
• nenhum esforço foi feito neste colab para realmente convergir,
• esforço mínimo foi feito para ajustar hiperparâmetros,
• nenhum esforço foi feito para regularizar ou pré-processar os dados (por exemplo, recursos do centro, etc.).

Conclusão

Neste colab, descrevemos modelos lineares generalizados de efeitos mistos e mostramos como usar a inferência variacional para ajustá-los usando a probabilidade do TensorFlow. Embora o problema do brinquedo tivesse apenas algumas centenas de amostras de treinamento, as técnicas usadas aqui são idênticas ao que é necessário em escala.