Pemilihan model Bayesian
 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Impor
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
Tugas: deteksi titik perubahan dengan beberapa titik perubahan
Pertimbangkan tugas deteksi titik perubahan: peristiwa terjadi pada tingkat yang berubah seiring waktu, didorong oleh perubahan mendadak dalam keadaan (tidak teramati) dari beberapa sistem atau proses yang menghasilkan data.
Misalnya, kita mungkin mengamati serangkaian hitungan seperti berikut:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
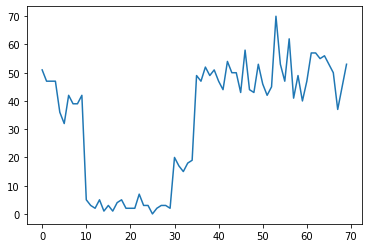
Ini dapat mewakili jumlah kegagalan di pusat data, jumlah pengunjung ke halaman web, jumlah paket pada tautan jaringan, dll.
Perhatikan bahwa tidak sepenuhnya jelas berapa banyak rezim sistem yang berbeda hanya dari melihat data. Bisakah Anda memberi tahu di mana masing-masing dari tiga titik sakelar itu terjadi?
Jumlah negara bagian yang diketahui
Pertama-tama kita akan mempertimbangkan kasus (mungkin tidak realistis) di mana jumlah keadaan yang tidak teramati diketahui secara apriori. Di sini, kita akan berasumsi bahwa kita tahu ada empat keadaan laten.
Kita model masalah ini sebagai switching (homogen) Proses Poisson: pada setiap titik waktu, jumlah peristiwa yang terjadi adalah Poisson didistribusikan, dan tingkat kejadian ditentukan oleh keadaan sistem yang tidak teramati \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
Negara-negara laten adalah diskrit: \(z_t \in \{1, 2, 3, 4\}\), sehingga \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) adalah vektor sederhana yang berisi tingkat Poisson untuk setiap negara. Untuk model evolusi negara dari waktu ke waktu, kita akan mendefinisikan sederhana transisi model \(p(z_t | z_{t-1})\): katakanlah bahwa pada setiap langkah kita tinggal di negara sebelumnya dengan beberapa probabilitas \(p\), dan dengan probabilitas \(1-p\) kami transisi ke keadaan yang berbeda seragam secara acak. Keadaan awal juga dipilih secara seragam secara acak, jadi kita memiliki:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
Asumsi ini sesuai dengan sebuah model yang Markov tersembunyi dengan emisi Poisson. Kita bisa mengkodekan mereka dalam TFP menggunakan tfd.HiddenMarkovModel . Pertama, kita mendefinisikan matriks transisi dan prior seragam pada keadaan awal:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
Berikutnya, kita membangun tfd.HiddenMarkovModel distribusi, menggunakan variabel dilatih untuk mewakili tingkat yang terkait dengan setiap sistem negara. Kami membuat parameter tarif di log-space untuk memastikan mereka bernilai positif.
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
Akhirnya, kita mendefinisikan total kerapatan log model, termasuk lognormal lemah-informatif sebelum pada tingkat, dan menjalankan optimizer untuk menghitung maksimum a posteriori (MAP) cocok untuk data count yang diamati.
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
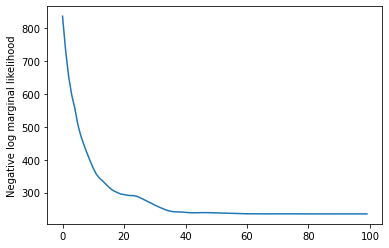
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
Itu berhasil! Perhatikan bahwa status laten dalam model ini hanya dapat diidentifikasi hingga permutasi, sehingga tingkat yang kami pulihkan berada dalam urutan yang berbeda, dan ada sedikit gangguan, tetapi umumnya mereka cukup cocok.
Memulihkan lintasan negara
Sekarang kita sudah cocok dengan model, kita mungkin ingin merekonstruksi yang model negara percaya sistem itu dalam setiap timestep.
Ini adalah tugas inferensi posterior: mengingat jumlah diamati \(x_{1:T}\) dan parameter model (tarif) \(\lambda\), kami ingin menyimpulkan urutan variabel laten diskrit, mengikuti posterior distribusi \(p(z_{1:T} | x_{1:T}, \lambda)\). Dalam model Markov yang tersembunyi, kita dapat secara efisien menghitung marjinal dan properti lain dari distribusi ini menggunakan algoritme penyampaian pesan standar. Secara khusus, posterior_marginals metode efisien akan menghitung (menggunakan algoritma maju-mundur ) marjinal distribusi probabilitas \(p(Z_t = z_t | x_{1:T})\) selama diskrit laten negara \(Z_t\) di setiap timestep \(t\).
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
Dengan memplot probabilitas posterior, kami memulihkan "penjelasan" model dari data: pada titik waktu mana setiap status aktif?
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
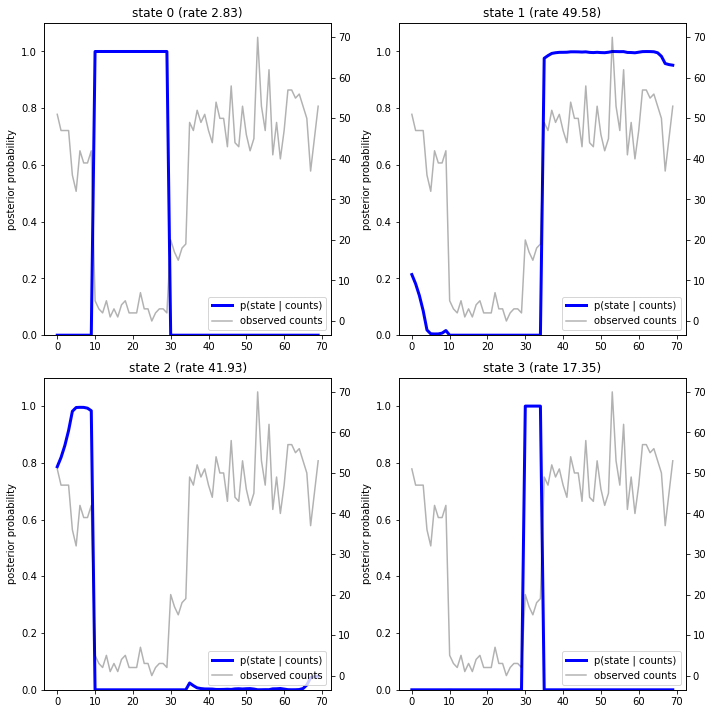
Dalam kasus (sederhana) ini, kita melihat bahwa model biasanya cukup percaya diri: pada sebagian besar langkah waktu model ini pada dasarnya menetapkan semua massa probabilitas ke salah satu dari empat keadaan. Untungnya, penjelasannya terlihat masuk akal!
Kami juga dapat memvisualisasikan posterior ini dalam hal tingkat terkait dengan negara laten yang paling mungkin pada setiap timestep, kondensasi posterior probabilistik menjadi penjelasan tunggal:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
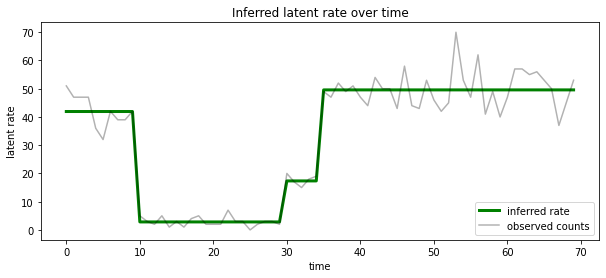
Jumlah negara bagian yang tidak diketahui
Dalam masalah nyata, kita mungkin tidak mengetahui jumlah status 'sebenarnya' dalam sistem yang kita modelkan. Ini mungkin tidak selalu menjadi perhatian: jika Anda tidak terlalu peduli dengan identitas status yang tidak diketahui, Anda bisa menjalankan model dengan status lebih dari yang Anda tahu akan dibutuhkan model, dan mempelajari (seperti) sekumpulan duplikat salinan dari keadaan sebenarnya. Tapi mari kita asumsikan Anda peduli untuk menyimpulkan jumlah status laten 'benar'.
Kita bisa melihat ini sebagai kasus Bayesian pemilihan model : kita memiliki satu set model kandidat, masing-masing dengan nomor yang berbeda dari negara laten, dan kami ingin memilih salah satu yang paling mungkin telah menghasilkan data yang diamati. Untuk melakukan ini, kita menghitung kemungkinan marjinal data di bawah masing-masing model (kami juga bisa menambahkan sebelum pada model sendiri, tapi itu tidak akan diperlukan dalam analisis ini, yang pisau cukur Bayesian Occam ternyata cukup untuk encode sebuah preferensi terhadap model yang lebih sederhana).
Sayangnya, kemungkinan marginal yang benar, yang terintegrasi lebih baik negara-negara diskrit \(z_{1:T}\) dan (vektor) parameter tingkat \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) tidak penurut untuk model ini. Untuk kenyamanan, kami akan perkiraan itu menggunakan apa yang disebut " Bayes empirik " atau "ketik II maksimum kemungkinan" Perkiraan: bukan sepenuhnya mengintegrasikan keluar parameter (tidak diketahui) tingkat \(\lambda\) terkait dengan setiap sistem negara, kami akan mengoptimalkan atas nilai-nilai mereka:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
Pendekatan ini mungkin overfit, yaitu akan lebih menyukai model yang lebih kompleks daripada kemungkinan marginal yang sebenarnya. Kita bisa mempertimbangkan perkiraan lebih setia, misalnya, mengoptimalkan variasional batas bawah, atau menggunakan Monte Carlo estimator seperti anil pengambilan sampel pentingnya ; ini (sayangnya) di luar cakupan notebook ini. (Untuk lebih lanjut tentang Bayesian pilihan model dan perkiraan, pasal 7 dari baik Machine Learning: a Probabilistik Perspektif adalah referensi yang baik.)
Pada prinsipnya, kita bisa melakukan perbandingan model ini hanya dengan Siarang optimalisasi atas berkali-kali dengan nilai yang berbeda dari num_states , tapi itu akan menjadi banyak pekerjaan. Di sini kita akan menunjukkan bagaimana untuk mempertimbangkan beberapa model secara paralel, menggunakan TFP ini batch_shape mekanisme vektorisasi.
Matriks transisi dan keadaan awal sebelum: daripada membangun deskripsi model tunggal, sekarang kita akan membangun sebuah batch matriks transisi dan logits sebelumnya, satu untuk masing-masing model calon hingga max_num_states . Untuk pengelompokan yang mudah, kita perlu memastikan bahwa semua perhitungan memiliki 'bentuk' yang sama: ini harus sesuai dengan dimensi model terbesar yang akan kita muat. Untuk menangani model yang lebih kecil, kita dapat 'menyematkan' deskripsinya di dimensi paling atas dari ruang keadaan, secara efektif memperlakukan dimensi yang tersisa sebagai keadaan tiruan yang tidak pernah digunakan.
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
Sekarang kita lanjutkan dengan cara yang sama seperti di atas. Kali ini kita akan menggunakan dimensi batch yang ekstra dalam trainable_rates untuk menyesuaikan secara terpisah tarif untuk masing-masing model dalam pertimbangan.
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
Dalam menghitung total log prob, kami berhati-hati untuk menjumlahkan hanya prior untuk tarif yang sebenarnya digunakan oleh setiap komponen model:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
Sekarang kita mengoptimalkan tujuan bets kita sudah dibangun, pas semua model kandidat secara bersamaan:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
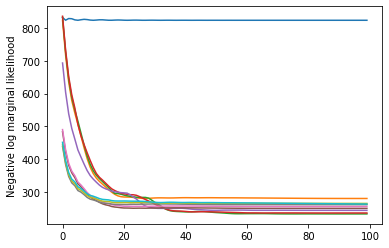
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
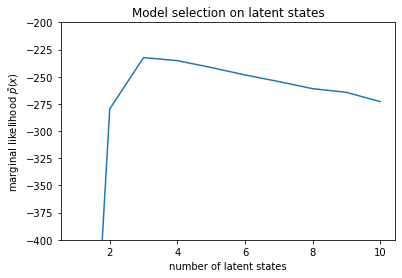
Meneliti kemungkinan, kita melihat bahwa kemungkinan marjinal (perkiraan) cenderung lebih memilih model tiga keadaan. Ini tampaknya cukup masuk akal -- model 'benar' memiliki empat status, tetapi hanya dengan melihat datanya, sulit untuk mengesampingkan penjelasan tiga status.
Kami juga dapat mengekstrak tarif yang sesuai untuk setiap model kandidat:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
Dan plot penjelasan yang diberikan setiap model untuk data:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
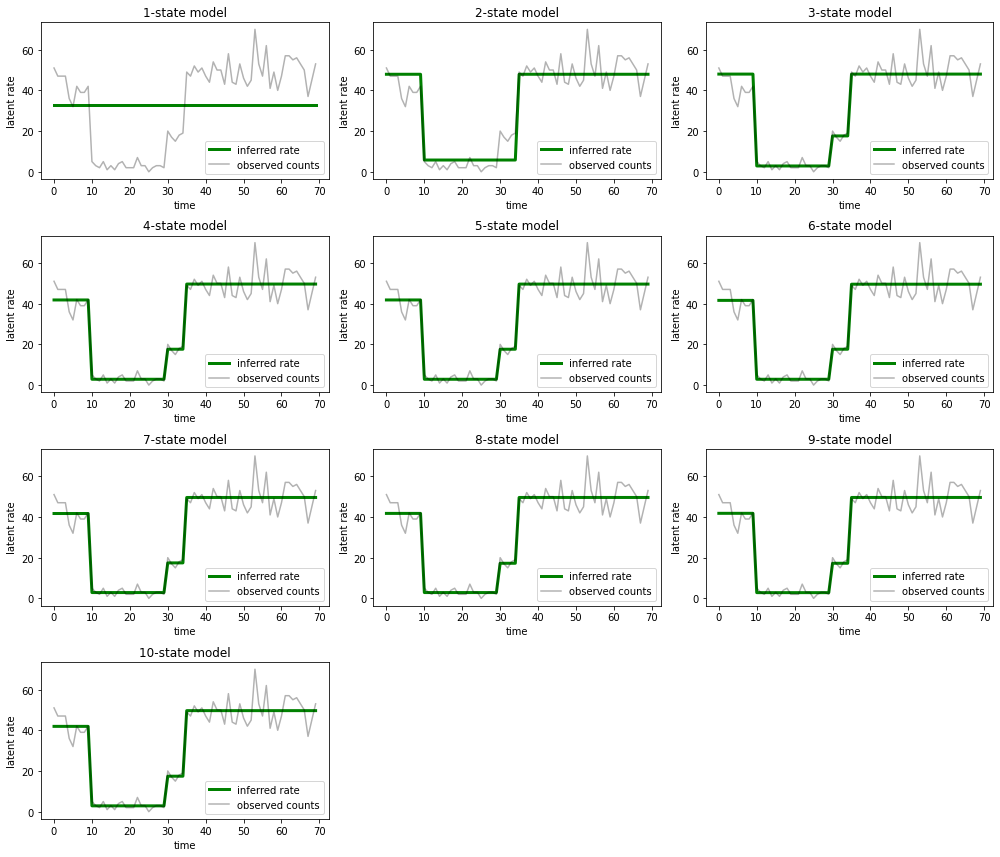
Sangat mudah untuk melihat bagaimana model satu, dua, dan (lebih halus) tiga keadaan memberikan penjelasan yang tidak memadai. Menariknya, semua model di atas empat negara bagian pada dasarnya memberikan penjelasan yang sama! Ini mungkin karena 'data' kami relatif bersih dan hanya menyisakan sedikit ruang untuk penjelasan alternatif; pada data dunia nyata yang lebih berantakan, kami mengharapkan model berkapasitas lebih tinggi untuk memberikan kecocokan yang lebih baik secara progresif dengan data, dengan beberapa titik tradeoff di mana kecocokan yang ditingkatkan melebihi kompleksitas model.
Ekstensi
Model-model di notebook ini dapat dengan mudah diperluas dalam banyak cara. Sebagai contoh:
- memungkinkan keadaan laten memiliki probabilitas yang berbeda (beberapa keadaan mungkin umum vs jarang)
- memungkinkan transisi yang tidak seragam antara keadaan laten (misalnya, untuk mengetahui bahwa mesin mogok biasanya diikuti oleh sistem reboot biasanya diikuti oleh periode kinerja yang baik, dll.)
- model emisi lainnya, misalnya
NegativeBinomialuntuk model yang bervariasi dispersi data count, atau distribusi kontinyu sepertiNormaluntuk data bernilai real.
