Perkiraan inferensi untuk model STS dengan pengamatan non-Gaussian

Lihat di TensorFlow.org Jalankan di Google Colab Lihat sumber di GitHub Unduh buku catatan

Notebook ini mendemonstrasikan penggunaan alat inferensi perkiraan TFP untuk menggabungkan model observasi (non-Gaussian) saat menyesuaikan dan memperkirakan dengan model deret waktu struktural (STS). Dalam contoh ini, kita akan menggunakan model observasi Poisson untuk bekerja dengan data hitungan diskrit.

import time
import matplotlib.pyplot as plt
import numpy as np

import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp

from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd

tf.enable_v2_behavior()

Data Sintetis

Pertama, kami akan membuat beberapa data hitungan sintetis:

num_timesteps = 30
observed_counts = np.round(3 + np.random.lognormal(np.log(np.linspace(
    num_timesteps, 5, num=num_timesteps)), 0.20, size=num_timesteps)) 
observed_counts = observed_counts.astype(np.float32)
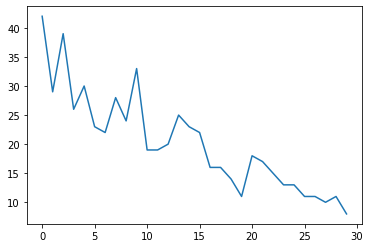
plt.plot(observed_counts)

[<matplotlib.lines.Line2D at 0x7f940ae958d0>]

png

Model

Kami akan menentukan model sederhana dengan tren linier berjalan secara acak:

def build_model(approximate_unconstrained_rates):
  trend = tfp.sts.LocalLinearTrend(
      observed_time_series=approximate_unconstrained_rates)
  return tfp.sts.Sum([trend],
                     observed_time_series=approximate_unconstrained_rates)

Alih-alih beroperasi pada deret waktu yang diamati, model ini akan beroperasi pada deret parameter laju Poisson yang mengatur pengamatan.

Karena tarif Poisson harus positif, kita akan menggunakan bijektor untuk mengubah model STS bernilai nyata menjadi distribusi di atas nilai positif. The Softplus transformasi \(y = \log(1 + \exp(x))\) adalah pilihan yang alami, karena hampir linear untuk nilai-nilai positif, tapi pilihan lain seperti Exp (yang mengubah normal random berjalan ke sebuah random walk lognormal) juga mungkin.

positive_bijector = tfb.Softplus()  # Or tfb.Exp()

# Approximate the unconstrained Poisson rate just to set heuristic priors.
# We could avoid this by passing explicit priors on all model params.
approximate_unconstrained_rates = positive_bijector.inverse(
    tf.convert_to_tensor(observed_counts) + 0.01)
sts_model = build_model(approximate_unconstrained_rates)

Untuk menggunakan inferensi perkiraan untuk model observasi non-Gaussian, kami akan mengkodekan model STS sebagai TFP JointDistribution. Variabel acak dalam distribusi gabungan ini adalah parameter model STS, deret waktu laju Poisson laten, dan hitungan yang diamati.

def sts_with_poisson_likelihood_model():
  # Encode the parameters of the STS model as random variables.
  param_vals = []
  for param in sts_model.parameters:
    param_val = yield param.prior
    param_vals.append(param_val)

  # Use the STS model to encode the log- (or inverse-softplus)
  # rate of a Poisson.
  unconstrained_rate = yield sts_model.make_state_space_model(
      num_timesteps, param_vals)
  rate = positive_bijector.forward(unconstrained_rate[..., 0])
  observed_counts = yield tfd.Poisson(rate, name='observed_counts')

model = tfd.JointDistributionCoroutineAutoBatched(sts_with_poisson_likelihood_model)

Persiapan untuk inferensi

Kami ingin menyimpulkan jumlah yang tidak teramati dalam model, mengingat jumlah yang diamati. Pertama, kami mengkondisikan kepadatan log gabungan pada hitungan yang diamati.

pinned_model = model.experimental_pin(observed_counts=observed_counts)

Kita juga memerlukan bijektor pembatas untuk memastikan bahwa inferensi mematuhi batasan pada parameter model STS (misalnya, skala harus positif).

constraining_bijector = pinned_model.experimental_default_event_space_bijector()

Inferensi dengan HMC

Kami akan menggunakan HMC (khususnya, NUTS) untuk sampel dari posterior sendi atas parameter model dan tingkat laten.

Ini akan jauh lebih lambat daripada menyesuaikan model STS standar dengan HMC, karena selain parameter model (jumlah yang relatif kecil) kita juga harus menyimpulkan seluruh rangkaian tarif Poisson. Jadi kita akan menjalankan sejumlah langkah yang relatif kecil; untuk aplikasi di mana kualitas inferensi sangat penting, mungkin masuk akal untuk meningkatkan nilai-nilai ini atau menjalankan banyak rantai.

Konfigurasi sampel

Pertama kita tentukan sampler, dan kemudian menggunakan sample_chain untuk menjalankan bahwa pengambilan sampel kernel untuk sampel produk.

sampler = tfp.mcmc.TransformedTransitionKernel(
    tfp.mcmc.NoUTurnSampler(
        target_log_prob_fn=pinned_model.unnormalized_log_prob,
        step_size=0.1),
    bijector=constraining_bijector)

adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
    inner_kernel=sampler,
    num_adaptation_steps=int(0.8 * num_burnin_steps),
    target_accept_prob=0.75)

initial_state = constraining_bijector.forward(
    type(pinned_model.event_shape)(
        *(tf.random.normal(part_shape)
          for part_shape in constraining_bijector.inverse_event_shape(
              pinned_model.event_shape))))

# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
  return tfp.mcmc.sample_chain(
      kernel=adaptive_sampler,
      current_state=initial_state,
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      trace_fn=None)

t0 = time.time()
samples = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))

Inference ran in 24.83s.

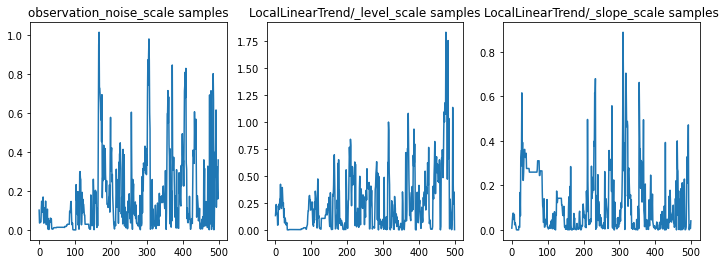
Kita dapat memeriksa kewarasan kesimpulan dengan memeriksa jejak parameter. Dalam hal ini mereka tampaknya telah mengeksplorasi beberapa penjelasan untuk data, yang bagus, meskipun lebih banyak sampel akan membantu untuk menilai seberapa baik rantai tersebut bercampur.

f = plt.figure(figsize=(12, 4))
for i, param in enumerate(sts_model.parameters):
  ax = f.add_subplot(1, len(sts_model.parameters), i + 1)
  ax.plot(samples[i])
  ax.set_title("{} samples".format(param.name))

png

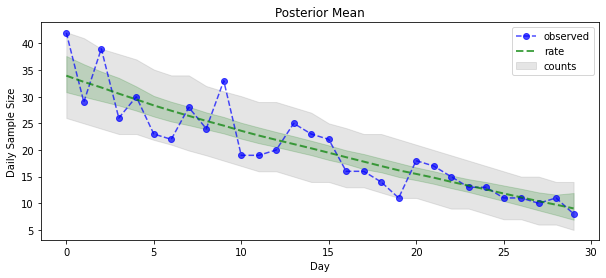
Sekarang untuk hasilnya: mari kita lihat posterior di atas tarif Poisson! Kami juga akan memplot interval prediktif 80% di atas jumlah yang diamati, dan dapat memeriksa apakah interval ini tampaknya mengandung sekitar 80% dari jumlah yang sebenarnya kami amati.

param_samples = samples[:-1]
unconstrained_rate_samples = samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)

plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(np.random.poisson(rate_samples), 
                                       [10, 90], axis=0)

_ = plt.plot(observed_counts, color="blue", ls='--', marker='o', label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color="green", ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey', label='counts', alpha=0.2)
plt.xlabel("Day")
plt.ylabel("Daily Sample Size")
plt.title("Posterior Mean")
plt.legend()

<matplotlib.legend.Legend at 0x7f93ffd35550>

png

Peramalan

Untuk memperkirakan jumlah yang diamati, kami akan menggunakan alat STS standar untuk membangun distribusi perkiraan atas tingkat laten (dalam ruang yang tidak dibatasi, sekali lagi karena STS dirancang untuk memodelkan data bernilai nyata), kemudian meneruskan perkiraan sampel melalui pengamatan Poisson model:

def sample_forecasted_counts(sts_model, posterior_latent_rates,
                             posterior_params, num_steps_forecast,
                             num_sampled_forecasts):

  # Forecast the future latent unconstrained rates, given the inferred latent
  # unconstrained rates and parameters.
  unconstrained_rates_forecast_dist = tfp.sts.forecast(sts_model,
    observed_time_series=unconstrained_rate_samples,
    parameter_samples=posterior_params,
    num_steps_forecast=num_steps_forecast)

  # Transform the forecast to positive-valued Poisson rates.
  rates_forecast_dist = tfd.TransformedDistribution(
      unconstrained_rates_forecast_dist,
      positive_bijector)

  # Sample from the forecast model following the chain rule:
  # P(counts) = P(counts | latent_rates)P(latent_rates)
  sampled_latent_rates = rates_forecast_dist.sample(num_sampled_forecasts)
  sampled_forecast_counts = tfd.Poisson(rate=sampled_latent_rates).sample()

  return sampled_forecast_counts, sampled_latent_rates

forecast_samples, rate_samples = sample_forecasted_counts(
   sts_model,
   posterior_latent_rates=unconstrained_rate_samples,
   posterior_params=param_samples,
   # Days to forecast:
   num_steps_forecast=30,
   num_sampled_forecasts=100)

forecast_samples = np.squeeze(forecast_samples)

def plot_forecast_helper(data, forecast_samples, CI=90):
  """Plot the observed time series alongside the forecast."""
  plt.figure(figsize=(10, 4))
  forecast_median = np.median(forecast_samples, axis=0)

  num_steps = len(data)
  num_steps_forecast = forecast_median.shape[-1]

  plt.plot(np.arange(num_steps), data, lw=2, color='blue', linestyle='--', marker='o',
           label='Observed Data', alpha=0.7)

  forecast_steps = np.arange(num_steps, num_steps+num_steps_forecast)

  CI_interval = [(100 - CI)/2, 100 - (100 - CI)/2]
  lower, upper = np.percentile(forecast_samples, CI_interval, axis=0)

  plt.plot(forecast_steps, forecast_median, lw=2, ls='--', marker='o', color='orange',
           label=str(CI) + '% Forecast Interval', alpha=0.7)
  plt.fill_between(forecast_steps,
                   lower,
                   upper, color='orange', alpha=0.2)

  plt.xlim([0, num_steps+num_steps_forecast])
  ymin, ymax = min(np.min(forecast_samples), np.min(data)), max(np.max(forecast_samples), np.max(data))
  yrange = ymax-ymin
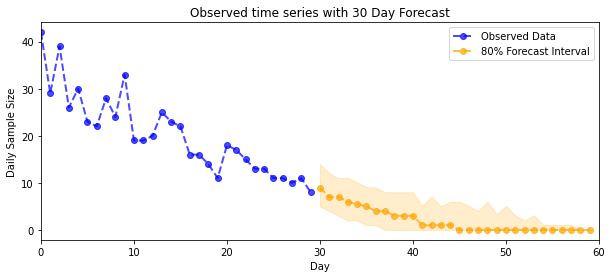
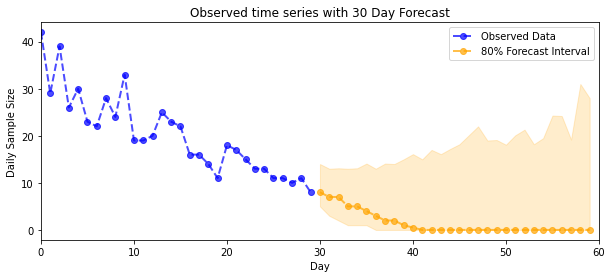
  plt.title("{}".format('Observed time series with ' + str(num_steps_forecast) + ' Day Forecast'))
  plt.xlabel('Day')
  plt.ylabel('Daily Sample Size')
  plt.legend()

plot_forecast_helper(observed_counts, forecast_samples, CI=80)

png

inferensi VI

Variasional inferensi dapat menjadi masalah ketika menyimpulkan waktu seri penuh, seperti jumlah perkiraan kami (sebagai lawan hanya parameter dari serangkaian waktu, seperti dalam model STS standar). Asumsi standar bahwa variabel memiliki posterior independen cukup salah, karena setiap langkah waktu berkorelasi dengan tetangganya, yang dapat menyebabkan ketidakpastian yang terlalu rendah. Untuk alasan ini, HMC mungkin menjadi pilihan yang lebih baik untuk perkiraan inferensi selama deret waktu penuh. Namun, VI bisa menjadi sedikit lebih cepat, dan mungkin berguna untuk model prototipe atau dalam kasus di mana kinerjanya dapat secara empiris terbukti 'cukup baik'.

Agar sesuai dengan model kami dengan VI, kami hanya membangun dan mengoptimalkan posterior pengganti:

surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
    event_shape=pinned_model.event_shape,
    bijector=constraining_bijector)

# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 1000 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)

t0 = time.time()
losses = tfp.vi.fit_surrogate_posterior(pinned_model.unnormalized_log_prob,
                                        surrogate_posterior,
                                        optimizer=tf.optimizers.Adam(0.1),
                                        num_steps=num_variational_steps)
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))

Inference ran in 11.37s.

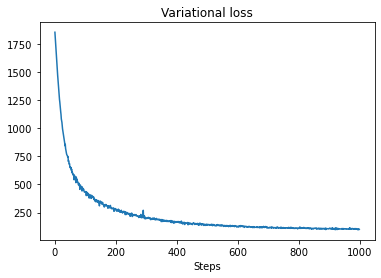
plt.plot(losses)
plt.title("Variational loss")
_ = plt.xlabel("Steps")

png

posterior_samples = surrogate_posterior.sample(50)
param_samples = posterior_samples[:-1]
unconstrained_rate_samples = posterior_samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)

plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(
    np.random.poisson(rate_samples), [10, 90], axis=0)

_ = plt.plot(observed_counts, color='blue', ls='--', marker='o',
             label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color='green',
             ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(
    np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey',
    label='counts', alpha=0.2)
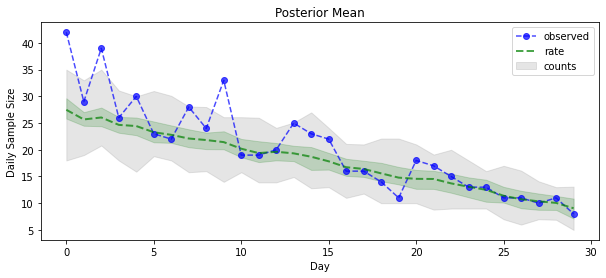
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.title('Posterior Mean')
plt.legend()

<matplotlib.legend.Legend at 0x7f93ff4735c0>

png

forecast_samples, rate_samples = sample_forecasted_counts(
   sts_model,
   posterior_latent_rates=unconstrained_rate_samples,
   posterior_params=param_samples,
   # Days to forecast:
   num_steps_forecast=30,
   num_sampled_forecasts=100)

forecast_samples = np.squeeze(forecast_samples)

plot_forecast_helper(observed_counts, forecast_samples, CI=80)

png