L'objectif de ce bloc-notes est d'aider TFP 0.12.1 à « prendre vie » via quelques petits extraits - de petites démonstrations de choses que vous pouvez réaliser avec TFP.
 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Installe et importe
!pip3 install -qU tensorflow==2.4.0 tensorflow_probability==0.12.1 tensorflow-datasets inference_gym
import tensorflow as tf
import tensorflow_probability as tfp
assert '0.12' in tfp.__version__, tfp.__version__
assert '2.4' in tf.__version__, tf.__version__
physical_devices = tf.config.list_physical_devices('CPU')
tf.config.set_logical_device_configuration(
physical_devices[0],
[tf.config.LogicalDeviceConfiguration(),
tf.config.LogicalDeviceConfiguration()])
tfd = tfp.distributions
tfb = tfp.bijectors
tfpk = tfp.math.psd_kernels
import matplotlib.pyplot as plt
import numpy as np
import scipy.interpolate
import IPython
import seaborn as sns
from inference_gym import using_tensorflow as gym
import logging
Bijecteurs
Glow
Un bijector du papier Glow: générative débit avec inversible 1x1 Convolutions , par Kingma et Dhariwal.
Voici comment dessiner une image à partir d'une distribution (notez que la distribution n'a rien "appris" ici).
image_shape = (32, 32, 4) # 32 x 32 RGBA image
glow = tfb.Glow(output_shape=image_shape,
coupling_bijector_fn=tfb.GlowDefaultNetwork,
exit_bijector_fn=tfb.GlowDefaultExitNetwork)
pz = tfd.Sample(tfd.Normal(0., 1.), tf.reduce_prod(image_shape))
# Calling glow on distribution p(z) creates our glow distribution over images.
px = glow(pz)
# Take samples from the distribution to get images from your dataset.
image = px.sample(1)[0].numpy()
# Rescale to [0, 1].
image = (image - image.min()) / (image.max() - image.min())
plt.imshow(image);

RayleighCDF
Bijector pour la de distribution de Rayleigh CDF. Une utilisation est l'échantillonnage à partir de la distribution de Rayleigh, en prélevant des échantillons uniformes, puis en les passant par l'inverse de la CDF.
bij = tfb.RayleighCDF()
uniforms = tfd.Uniform().sample(10_000)
plt.hist(bij.inverse(uniforms), bins='auto');

Ascending() remplace Invert(Ordered())
x = tfd.Normal(0., 1.).sample(5)
print(tfb.Ascending()(x))
print(tfb.Invert(tfb.Ordered())(x))
tf.Tensor([1.9363368 2.650928 3.4936204 4.1817293 5.6920815], shape=(5,), dtype=float32) WARNING:tensorflow:From <ipython-input-5-1406b9939c00>:3: Ordered.__init__ (from tensorflow_probability.python.bijectors.ordered) is deprecated and will be removed after 2021-01-09. Instructions for updating: `Ordered` bijector is deprecated; please use `tfb.Invert(tfb.Ascending())` instead. tf.Tensor([1.9363368 2.650928 3.4936204 4.1817293 5.6920815], shape=(5,), dtype=float32)
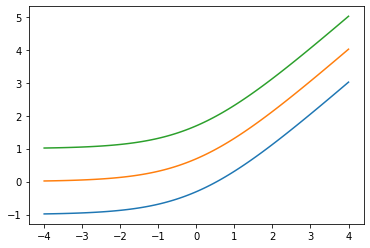
Ajouter low arg: Softplus(low=2.)
x = tf.linspace(-4., 4., 100)
for low in (-1., 0., 1.):
bij = tfb.Softplus(low=low)
plt.plot(x, bij(x));
tfb.ScaleMatvecLinearOperatorBlock supporte par blocs LinearOperator , args plusieurs parties
op_1 = tf.linalg.LinearOperatorDiag(diag=[1., -1., 3.])
op_2 = tf.linalg.LinearOperatorFullMatrix([[12., 5.], [-1., 3.]])
scale = tf.linalg.LinearOperatorBlockDiag([op_1, op_2], is_non_singular=True)
bij = tfb.ScaleMatvecLinearOperatorBlock(scale)
bij([[1., 2., 3.], [0., 1.]])
WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/ops/linalg/linear_operator_block_diag.py:223: LinearOperator.graph_parents (from tensorflow.python.ops.linalg.linear_operator) is deprecated and will be removed in a future version. Instructions for updating: Do not call `graph_parents`. [<tf.Tensor: shape=(3,), dtype=float32, numpy=array([ 1., -2., 9.], dtype=float32)>, <tf.Tensor: shape=(2,), dtype=float32, numpy=array([5., 3.], dtype=float32)>]
Répartition
Skellam
La distribution sur les différences de deux Poisson VR. Notez que les échantillons de cette distribution peuvent être négatifs.
x = tf.linspace(-5., 10., 10 - -5 + 1)
rates = (4, 2)
for i, rate in enumerate(rates):
plt.bar(x - .3 * (1 - i), tfd.Poisson(rate).prob(x), label=f'Poisson({rate})', alpha=0.5, width=.3)
plt.bar(x.numpy() + .3, tfd.Skellam(*rates).prob(x).numpy(), color='k', alpha=0.25, width=.3,
label=f'Skellam{rates}')
plt.legend();

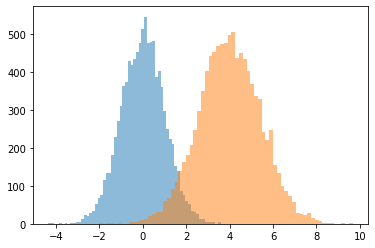
JointDistributionCoroutine[AutoBatched] produits namedtuple -comme échantillons
Explicitement spécifier sample_dtype=[...] pour l'ancien tuple comportement.
@tfd.JointDistributionCoroutineAutoBatched
def model():
x = yield tfd.Normal(0., 1., name='x')
y = x + 4.
yield tfd.Normal(y, 1., name='y')
draw = model.sample(10_000)
plt.hist(draw.x, bins='auto', alpha=0.5)
plt.hist(draw.y, bins='auto', alpha=0.5);
WARNING:tensorflow:Note that RandomStandardNormal inside pfor op may not give same output as inside a sequential loop. WARNING:tensorflow:Note that RandomStandardNormal inside pfor op may not give same output as inside a sequential loop.
VonMisesFisher supports dim > 5 , entropy()
La distribution de \(n-1\) \(\mathbb{R}^n\)von Mises-Fisher est une distribution sur le \(n-1\) sphère dimensionnelle \(\mathbb{R}^n\).
dist = tfd.VonMisesFisher([0., 1, 0, 1, 0, 1], concentration=1.)
draws = dist.sample(3)
print(dist.entropy())
tf.reduce_sum(draws ** 2, axis=1) # each draw has length 1
tf.Tensor(3.3533673, shape=(), dtype=float32) <tf.Tensor: shape=(3,), dtype=float32, numpy=array([1.0000002 , 0.99999994, 1.0000001 ], dtype=float32)>
ExpGamma , ExpInverseGamma
log_rate paramètre ajouté à Gamma . Améliorations numériques lors de l' échantillonnage à faible concentration Beta , Dirichlet et amis. Gradients de reparamétrage implicites dans tous les cas.
plt.figure(figsize=(10, 3))
plt.subplot(121)
plt.hist(tfd.Beta(.02, .02).sample(10_000), bins='auto')
plt.title('Beta(.02, .02)')
plt.subplot(122)
plt.title('GamX/(GamX+GamY) [the old way]')
g = tfd.Gamma(.02, 1); s0, s1 = g.sample(10_000), g.sample(10_000)
plt.hist(s0 / (s0 + s1), bins='auto')
plt.show()
plt.figure(figsize=(10, 3))
plt.subplot(121)
plt.hist(tfd.ExpGamma(.02, 1.).sample(10_000), bins='auto')
plt.title('ExpGamma(.02, 1)')
plt.subplot(122)
plt.hist(tfb.Log()(tfd.Gamma(.02, 1.)).sample(10_000), bins='auto')
plt.title('tfb.Log()(Gamma(.02, 1)) [the old way]');


JointDistribution*AutoBatched supporte échantillonnage reproductible (avec tuple / graines Tenseur longueur-2)
@tfd.JointDistributionCoroutineAutoBatched
def model():
x = yield tfd.Normal(0, 1, name='x')
y = yield tfd.Normal(x + 4, 1, name='y')
print(model.sample(seed=(1, 2)))
print(model.sample(seed=(1, 2)))
StructTuple( x=<tf.Tensor: shape=(), dtype=float32, numpy=-0.59835213>, y=<tf.Tensor: shape=(), dtype=float32, numpy=6.2380724> ) StructTuple( x=<tf.Tensor: shape=(), dtype=float32, numpy=-0.59835213>, y=<tf.Tensor: shape=(), dtype=float32, numpy=6.2380724> )
KL(VonMisesFisher || SphericalUniform)
# Build vMFs with the same mean direction, batch of increasing concentrations.
vmf = tfd.VonMisesFisher(tf.math.l2_normalize(tf.random.normal([10])),
concentration=[0., .1, 1., 10.])
# KL increases with concentration, since vMF(conc=0) == SphericalUniform.
print(tfd.kl_divergence(vmf, tfd.SphericalUniform(10)))
tf.Tensor([4.7683716e-07 4.9877167e-04 4.9384594e-02 2.4844694e+00], shape=(4,), dtype=float32)
parameter_properties
Cours de distribution exposent maintenant un parameter_properties(dtype=tf.float32, num_classes=None) méthode de classe, ce qui peut permettre la construction automatisée de nombreuses classes de distributions.
print('Gamma:', tfd.Gamma.parameter_properties())
print('Categorical:', tfd.Categorical.parameter_properties(dtype=tf.float64, num_classes=7))
Gamma: {'concentration': ParameterProperties(event_ndims=0, shape_fn=<function ParameterProperties.<lambda> at 0x7ff6bbfcdd90>, default_constraining_bijector_fn=<function Gamma._parameter_properties.<locals>.<lambda> at 0x7ff6afd95510>, is_preferred=True), 'rate': ParameterProperties(event_ndims=0, shape_fn=<function ParameterProperties.<lambda> at 0x7ff6bbfcdd90>, default_constraining_bijector_fn=<function Gamma._parameter_properties.<locals>.<lambda> at 0x7ff6afd95ea0>, is_preferred=False), 'log_rate': ParameterProperties(event_ndims=0, shape_fn=<function ParameterProperties.<lambda> at 0x7ff6bbfcdd90>, default_constraining_bijector_fn=<class 'tensorflow_probability.python.bijectors.identity.Identity'>, is_preferred=True)}
Categorical: {'logits': ParameterProperties(event_ndims=1, shape_fn=<function Categorical._parameter_properties.<locals>.<lambda> at 0x7ff6afd95510>, default_constraining_bijector_fn=<class 'tensorflow_probability.python.bijectors.identity.Identity'>, is_preferred=True), 'probs': ParameterProperties(event_ndims=1, shape_fn=<function Categorical._parameter_properties.<locals>.<lambda> at 0x7ff6afdc91e0>, default_constraining_bijector_fn=<class 'tensorflow_probability.python.bijectors.softmax_centered.SoftmaxCentered'>, is_preferred=False)}
experimental_default_event_space_bijector
Accepte désormais des arguments supplémentaires épinglant certaines parties de la distribution.
@tfd.JointDistributionCoroutineAutoBatched
def model():
scale = yield tfd.Gamma(1, 1, name='scale')
obs = yield tfd.Normal(0, scale, name='obs')
model.experimental_default_event_space_bijector(obs=.2).forward(
[tf.random.uniform([3], -2, 2.)])
StructTuple( scale=<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.6630705, 1.5401832, 1.0777743], dtype=float32)> )
JointDistribution.experimental_pin
Pins quelques pièces de distribution communes, retour JointDistributionPinned objet représentant la densité non normalisée commune.
Travailler avec le experimental_default_event_space_bijector , cela fait faire l' inférence variationnelle ou MCCM avec bon sens par défaut beaucoup plus simple. Dans le exemple ci - dessous, les deux premières lignes de l' sample font courir MCMC un jeu d' enfant.
dist = tfd.JointDistributionSequential([
tfd.HalfNormal(1.),
lambda scale: tfd.Normal(0., scale, name='observed')])
@tf.function
def sample():
bij = dist.experimental_default_event_space_bijector(observed=1.)
target_log_prob = dist.experimental_pin(observed=1.).unnormalized_log_prob
kernel = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.HamiltonianMonteCarlo(target_log_prob,
step_size=0.6,
num_leapfrog_steps=16),
bijector=bij)
return tfp.mcmc.sample_chain(500,
current_state=tf.ones([8]), # multiple chains
kernel=kernel,
trace_fn=None)
draws = sample()
fig, (hist, trace) = plt.subplots(ncols=2, figsize=(16, 3))
trace.plot(draws, alpha=0.5)
for col in tf.transpose(draws):
sns.kdeplot(col, ax=hist);

tfd.NegativeBinomial.experimental_from_mean_dispersion
Paramétrage alternatif. Envoyez un e-mail à tfprobability@tensorflow.org ou envoyez-nous un PR pour ajouter des méthodes de classe similaires pour d'autres distributions.
nb = tfd.NegativeBinomial.experimental_from_mean_dispersion(30., .01)
plt.hist(nb.sample(10_000), bins='auto');

tfp.experimental.distribute
DistributionStrategy -Aware distributions communes, ce qui permet pour les calculs de probabilité multi-appareils. Fragmentées Independent et Sample distributions.
# Note: 2-logical devices are configured in the install/import cell at top.
strategy = tf.distribute.MirroredStrategy()
assert strategy.num_replicas_in_sync == 2
@tfp.experimental.distribute.JointDistributionCoroutine
def model():
root = tfp.experimental.distribute.JointDistributionCoroutine.Root
group_scale = yield root(tfd.Sample(tfd.Exponential(1), 3, name='group_scale'))
_ = yield tfp.experimental.distribute.ShardedSample(tfd.Independent(tfd.Normal(0, group_scale), 1),
sample_shape=[4], name='x')
seed1, seed2 = tfp.random.split_seed((1, 2))
@tf.function
def sample(seed):
return model.sample(seed=seed)
xs = strategy.run(sample, (seed1,))
print("""
Note that the global latent `group_scale` is shared across devices, whereas
the local `x` is sampled independently on each device.
""")
print('sample:', xs)
print('another sample:', strategy.run(sample, (seed2,)))
@tf.function
def log_prob(x):
return model.log_prob(x)
print("""
Note that each device observes the same log_prob (local latent log_probs are
summed across devices).
""")
print('log_prob:', strategy.run(log_prob, (xs,)))
@tf.function
def grad_log_prob(x):
return tfp.math.value_and_gradient(model.log_prob, x)[1]
print("""
Note that each device observes the same log_prob gradient (local latents have
independent gradients, global latents have gradients aggregated across devices).
""")
print('grad_log_prob:', strategy.run(grad_log_prob, (xs,)))
WARNING:tensorflow:There are non-GPU devices in `tf.distribute.Strategy`, not using nccl allreduce.
INFO:tensorflow:Using MirroredStrategy with devices ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1')
Note that the global latent `group_scale` is shared across devices, whereas
the local `x` is sampled independently on each device.
sample: StructTuple(
group_scale=PerReplica:{
0: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([2.6355493, 1.1805456, 1.245112 ], dtype=float32)>,
1: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([2.6355493, 1.1805456, 1.245112 ], dtype=float32)>
},
x=PerReplica:{
0: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[-0.90548456, 0.7675636 , 0.27627748],
[-0.3475989 , 2.0194046 , -1.2531326 ]], dtype=float32)>,
1: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[ 3.251305 , -0.5790973 , 0.42745453],
[-1.562331 , 0.3006323 , 0.635732 ]], dtype=float32)>
}
)
another sample: StructTuple(
group_scale=PerReplica:{
0: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([2.41133 , 0.10307606, 0.5236566 ], dtype=float32)>,
1: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([2.41133 , 0.10307606, 0.5236566 ], dtype=float32)>
},
x=PerReplica:{
0: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[-3.2476294 , 0.07213175, -0.39536062],
[-1.2319602 , -0.05505352, 0.06356457]], dtype=float32)>,
1: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[ 5.6028705 , 0.11919801, -0.48446828],
[-1.5938259 , 0.21123725, 0.28979057]], dtype=float32)>
}
)
Note that each device observes the same log_prob (local latent log_probs are
summed across devices).
INFO:tensorflow:Reduce to /job:localhost/replica:0/task:0/device:CPU:0 then broadcast to ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1').
log_prob: PerReplica:{
0: tf.Tensor(-25.05747, shape=(), dtype=float32),
1: tf.Tensor(-25.05747, shape=(), dtype=float32)
}
Note that each device observes the same log_prob gradient (local latents have
independent gradients, global latents are aggregated across devices).
INFO:tensorflow:Reduce to /job:localhost/replica:0/task:0/device:CPU:0 then broadcast to ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1').
INFO:tensorflow:Reduce to /job:localhost/replica:0/task:0/device:CPU:0 then broadcast to ('/job:localhost/replica:0/task:0/device:CPU:0', '/job:localhost/replica:0/task:0/device:CPU:1').
grad_log_prob: StructTuple(
group_scale=PerReplica:{
0: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.7555585, -1.2928739, -3.0554674], dtype=float32)>,
1: <tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.7555585, -1.2928739, -3.0554674], dtype=float32)>
},
x=PerReplica:{
0: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[ 0.13035832, -0.5507428 , -0.17820862],
[ 0.05004217, -1.4489648 , 0.80831426]], dtype=float32)>,
1: <tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[-0.46807498, 0.41551432, -0.27572307],
[ 0.22492138, -0.21570992, -0.41006932]], dtype=float32)>
}
)
Noyaux PSD
GeneralizedMatern
Le GeneralizedMatern positif semidéfinie noyau généralise MaternOneHalf , MAterhThreeHalves et MaternFiveHalves .
gm = tfpk.GeneralizedMatern(df=[0.5, 1.5, 2.5], length_scale=1., amplitude=0.5)
m1 = tfpk.MaternOneHalf(length_scale=1., amplitude=0.5)
m2 = tfpk.MaternThreeHalves(length_scale=1., amplitude=0.5)
m3 = tfpk.MaternFiveHalves(length_scale=1., amplitude=0.5)
xs = tf.linspace(-1.5, 1.5, 100)
gm_matrix = gm.matrix([[0.]], xs[..., tf.newaxis])
plt.plot(xs, gm_matrix[0][0])
plt.plot(xs, m1.matrix([[0.]], xs[..., tf.newaxis])[0])
plt.show()
plt.plot(xs, gm_matrix[1][0])
plt.plot(xs, m2.matrix([[0.]], xs[..., tf.newaxis])[0])
plt.show()
plt.plot(xs, gm_matrix[2][0])
plt.plot(xs, m3.matrix([[0.]], xs[..., tf.newaxis])[0])
plt.show()



Parabolic (Epanechnikov)
epa = tfpk.Parabolic()
xs = tf.linspace(-1.05, 1.05, 100)
plt.plot(xs, epa.matrix([[0.]], xs[..., tf.newaxis])[0]);

VI
build_asvi_surrogate_posterior
Construisez automatiquement une postérieure de substitution structurée pour VI d'une manière qui incorpore la structure graphique de la distribution antérieure. Ceci utilise la méthode décrite dans le document automatique structuré Variational Inference ( https://arxiv.org/abs/2002.00643 ).
# Import a Brownian Motion model from TFP's inference gym.
model = gym.targets.BrownianMotionMissingMiddleObservations()
prior = model.prior_distribution()
ground_truth = ground_truth = model.sample_transformations['identity'].ground_truth_mean
target_log_prob = lambda *values: model.log_likelihood(values) + prior.log_prob(values)
Ceci modélise un processus de mouvement brownien avec un modèle d'observation gaussien. Il se compose de 30 pas de temps, mais les 10 pas de temps du milieu sont inobservables.
locs[0] ~ Normal(loc=0, scale=innovation_noise_scale)
for t in range(1, num_timesteps):
locs[t] ~ Normal(loc=locs[t - 1], scale=innovation_noise_scale)
for t in range(num_timesteps):
observed_locs[t] ~ Normal(loc=locs[t], scale=observation_noise_scale)
L'objectif est de déduire les valeurs de locs à partir d' observations bruyantes ( observed_locs ). Depuis les 10 intermédiaires sont inobservables pas de temps, observed_locs sont NaN valeurs à pas de temps [10,19].
# The observed loc values in the Brownian Motion inference gym model
OBSERVED_LOC = np.array([
0.21592641, 0.118771404, -0.07945447, 0.037677474, -0.27885845, -0.1484156,
-0.3250906, -0.22957903, -0.44110894, -0.09830782, np.nan, np.nan, np.nan,
np.nan, np.nan, np.nan, np.nan, np.nan, np.nan, np.nan, -0.8786016,
-0.83736074, -0.7384849, -0.8939254, -0.7774566, -0.70238715, -0.87771565,
-0.51853573, -0.6948214, -0.6202789
]).astype(dtype=np.float32)
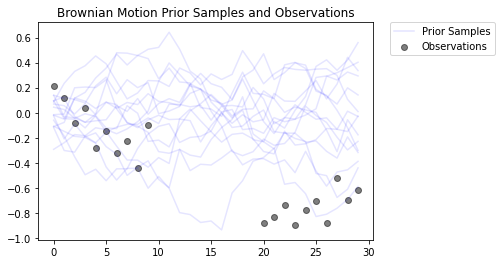
# Plot the prior and the likelihood observations
plt.figure()
plt.title('Brownian Motion Prior Samples and Observations')
num_samples = 15
prior_samples = prior.sample(num_samples)
plt.plot(prior_samples, c='blue', alpha=0.1)
plt.plot(prior_samples[0][0], label="Prior Samples", c='blue', alpha=0.1)
plt.scatter(x=range(30),y=OBSERVED_LOC, c='black', alpha=0.5, label="Observations")
plt.legend(bbox_to_anchor=(1.05, 1), borderaxespad=0.);
logging.getLogger('tensorflow').setLevel(logging.ERROR) # suppress pfor warnings
# Construct and train an ASVI Surrogate Posterior.
asvi_surrogate_posterior = tfp.experimental.vi.build_asvi_surrogate_posterior(prior)
asvi_losses = tfp.vi.fit_surrogate_posterior(target_log_prob,
asvi_surrogate_posterior,
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=500)
logging.getLogger('tensorflow').setLevel(logging.NOTSET)
# Construct and train a Mean-Field Surrogate Posterior.
factored_surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(event_shape=prior.event_shape)
factored_losses = tfp.vi.fit_surrogate_posterior(target_log_prob,
factored_surrogate_posterior,
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=500)
logging.getLogger('tensorflow').setLevel(logging.ERROR) # suppress pfor warnings
# Sample from the posteriors.
asvi_posterior_samples = asvi_surrogate_posterior.sample(num_samples)
factored_posterior_samples = factored_surrogate_posterior.sample(num_samples)
logging.getLogger('tensorflow').setLevel(logging.NOTSET)
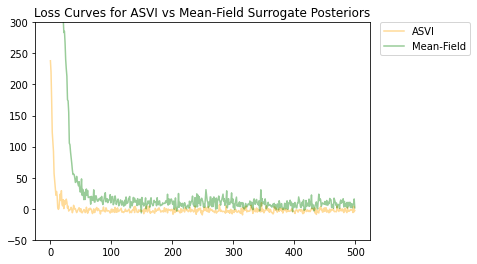
Les distributions postérieures ASVI et de substitution à champ moyen ont toutes deux convergé, et la postérieure ASVI de substitution avait une perte finale plus faible (valeur ELBO négative).
# Plot the loss curves.
plt.figure()
plt.title('Loss Curves for ASVI vs Mean-Field Surrogate Posteriors')
plt.plot(asvi_losses, c='orange', label='ASVI', alpha = 0.4)
plt.plot(factored_losses, c='green', label='Mean-Field', alpha = 0.4)
plt.ylim(-50, 300)
plt.legend(bbox_to_anchor=(1.3, 1), borderaxespad=0.);
Les échantillons des postérieurs soulignent à quel point le postérieur de substitution ASVI capture bien l'incertitude pour les pas de temps sans observations. D'autre part, le champ moyen a posteriori a du mal à saisir la véritable incertitude.
# Plot samples from the ASVI and Mean-Field Surrogate Posteriors.
plt.figure()
plt.title('Posterior Samples from ASVI vs Mean-Field Surrogate Posterior')
plt.plot(asvi_posterior_samples, c='orange', alpha = 0.25)
plt.plot(asvi_posterior_samples[0][0], label='ASVI Surrogate Posterior', c='orange', alpha = 0.25)
plt.plot(factored_posterior_samples, c='green', alpha = 0.25)
plt.plot(factored_posterior_samples[0][0], label='Mean-Field Surrogate Posterior', c='green', alpha = 0.25)
plt.scatter(x=range(30),y=OBSERVED_LOC, c='black', alpha=0.5, label='Observations')
plt.plot(ground_truth, c='black', label='Ground Truth')
plt.legend(bbox_to_anchor=(1.585, 1), borderaxespad=0.);

MCMC
ProgressBarReducer
Visualisez la progression de l'échantillonneur. (Peut avoir une pénalité de performance nominale ; pas actuellement pris en charge par la compilation JIT.)
kernel = tfp.mcmc.HamiltonianMonteCarlo(lambda x: -x**2 / 2, .05, 20)
pbar = tfp.experimental.mcmc.ProgressBarReducer(100)
kernel = tfp.experimental.mcmc.WithReductions(kernel, pbar)
plt.hist(tf.reshape(tfp.mcmc.sample_chain(100, current_state=tf.ones([128]), kernel=kernel, trace_fn=None), [-1]), bins='auto')
pbar.bar.close()
99%|█████████▉| 99/100 [00:03<00:00, 27.37it/s]
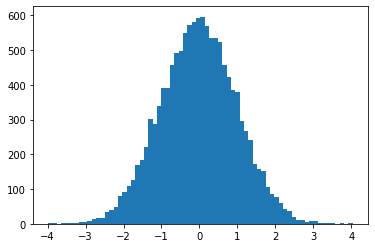
sample_sequential_monte_carlo supporte échantillonnage reproductible
initial_state = tf.random.uniform([4096], -2., 2.)
def smc(seed):
return tfp.experimental.mcmc.sample_sequential_monte_carlo(
prior_log_prob_fn=lambda x: -x**2 / 2,
likelihood_log_prob_fn=lambda x: -(x-1.)**2 / 2,
current_state=initial_state,
seed=seed)[1]
plt.hist(smc(seed=(12, 34)), bins='auto');plt.show()
print(smc(seed=(12, 34))[:10])
print('different:', smc(seed=(10, 20))[:10])
print('same:', smc(seed=(12, 34))[:10])

tf.Tensor( [ 0.665834 0.9892149 0.7961128 1.0016634 -1.000767 -0.19461267 1.3070581 1.127177 0.9940303 0.58239716], shape=(10,), dtype=float32) different: tf.Tensor( [ 1.3284367 0.4374407 1.1349089 0.4557473 0.06510283 -0.08954388 1.1735026 0.8170528 0.12443061 0.34413314], shape=(10,), dtype=float32) same: tf.Tensor( [ 0.665834 0.9892149 0.7961128 1.0016634 -1.000767 -0.19461267 1.3070581 1.127177 0.9940303 0.58239716], shape=(10,), dtype=float32)
Ajout de calculs en continu de variance, covariance, Rhat
Remarque, les interfaces de ceux - ci ont quelque peu changé tfp-nightly .
def cov_to_ellipse(t, cov, mean):
"""Draw a one standard deviation ellipse from the mean, according to cov."""
diag = tf.linalg.diag_part(cov)
a = 0.5 * tf.reduce_sum(diag)
b = tf.sqrt(0.25 * (diag[0] - diag[1])**2 + cov[0, 1]**2)
major = a + b
minor = a - b
theta = tf.math.atan2(major - cov[0, 0], cov[0, 1])
x = (tf.sqrt(major) * tf.cos(theta) * tf.cos(t) -
tf.sqrt(minor) * tf.sin(theta) * tf.sin(t))
y = (tf.sqrt(major) * tf.sin(theta) * tf.cos(t) +
tf.sqrt(minor) * tf.cos(theta) * tf.sin(t))
return x + mean[0], y + mean[1]
fig, axes = plt.subplots(nrows=4, ncols=5, figsize=(14, 8),
sharex=True, sharey=True, constrained_layout=True)
t = tf.linspace(0., 2 * np.pi, 200)
tot = 10
cov = 0.1 * tf.eye(2) + 0.9 * tf.ones([2, 2])
mvn = tfd.MultivariateNormalTriL(loc=[1., 2.],
scale_tril=tf.linalg.cholesky(cov))
for ax in axes.ravel():
rv = tfp.experimental.stats.RunningCovariance(
num_samples=0., mean=tf.zeros(2), sum_squared_residuals=tf.zeros((2, 2)),
event_ndims=1)
for idx, x in enumerate(mvn.sample(tot)):
rv = rv.update(x)
ax.plot(*cov_to_ellipse(t, rv.covariance(), rv.mean),
color='k', alpha=(idx + 1) / tot)
ax.plot(*cov_to_ellipse(t, mvn.covariance(), mvn.mean()), 'r')
fig.suptitle("Twenty tries to approximate the red covariance with 10 draws");

Mathématiques, statistiques
Fonctions de Bessel : ive, kve, log-ive
xs = tf.linspace(0.5, 20., 100)
ys = tfp.math.bessel_ive([[0.5], [1.], [np.pi], [4.]], xs)
zs = tfp.math.bessel_kve([[0.5], [1.], [2.], [np.pi]], xs)
for i in range(4):
plt.plot(xs, ys[i])
plt.show()
for i in range(4):
plt.plot(xs, zs[i])
plt.show()


Facultatif weights arg à tfp.stats.histogram
edges = tf.linspace(-4., 4, 31)
samps = tfd.TruncatedNormal(0, 1, -4, 4).sample(100_000, seed=(123, 456))
_, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3))
ax1.bar(edges[:-1], tfp.stats.histogram(samps, edges))
ax1.set_title('samples histogram')
ax2.bar(edges[:-1], tfp.stats.histogram(samps, edges, weights=1 / tfd.Normal(0, 1).prob(samps)))
ax2.set_title('samples, weighted by inverse p(sample)');

tfp.math.erfcinv
x = tf.linspace(-3., 3., 10)
y = tf.math.erfc(x)
z = tfp.math.erfcinv(y)
print(x)
print(z)
tf.Tensor( [-3. -2.3333333 -1.6666666 -1. -0.33333325 0.3333335 1. 1.666667 2.3333335 3. ], shape=(10,), dtype=float32) tf.Tensor( [-3.0002644 -2.3333426 -1.6666666 -0.9999997 -0.3333332 0.33333346 0.9999999 1.6666667 2.3333335 3.0000002 ], shape=(10,), dtype=float32)
