اختيار نموذج بايزي
 عرض على TensorFlow.org عرض على TensorFlow.org |  تشغيل في Google Colab تشغيل في Google Colab |  عرض المصدر على جيثب عرض المصدر على جيثب |  تحميل دفتر تحميل دفتر |
الواردات
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
المهمة: كشف نقاط التغيير مع نقاط التغيير المتعددة
ضع في اعتبارك مهمة اكتشاف نقطة التغيير: تحدث الأحداث بمعدل يتغير بمرور الوقت ، مدفوعًا بالتحولات المفاجئة في الحالة (غير المرصودة) لبعض الأنظمة أو العمليات التي تولد البيانات.
على سبيل المثال ، قد نلاحظ سلسلة من التهم كما يلي:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
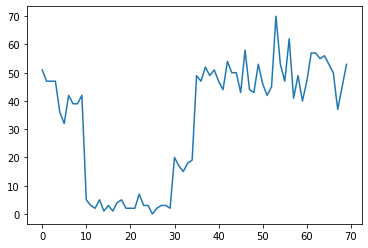
يمكن أن يمثل ذلك عدد حالات الفشل في مركز البيانات ، وعدد زوار صفحة الويب ، وعدد الحزم على ارتباط الشبكة ، وما إلى ذلك.
لاحظ أنه ليس من الواضح تمامًا عدد أنظمة النظام المتميزة الموجودة بمجرد النظر إلى البيانات. هل يمكنك معرفة مكان حدوث كل نقطة من نقاط التبديل الثلاثة؟
عدد الدول المعروف
سننظر أولاً في الحالة (التي قد تكون غير واقعية) حيث يُعرف عدد الحالات غير المرصودة مسبقًا. هنا ، سنفترض أننا نعلم أن هناك أربع حالات كامنة.
نحن نموذج هذه المشكلة بوصفها التحول (غير متجانسة) عملية بواسون: في كل نقطة في الوقت المناسب، وعدد من الأحداث التي تحدث هو بواسون الموزعة، ويتم تحديد سعر للأحداث من قبل غير الملحوظ حالة النظام \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
دول الكامنة هي منفصلة: \(z_t \in \{1, 2, 3, 4\}\)، لذلك \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) متجه بسيطة تحتوي على نسبة بواسون لكل دولة. لنموذج تطور الدول مع مرور الوقت، سنقوم بتعريف بسيط نموذج التحول \(p(z_t | z_{t-1})\): دعنا نقول أن نبقى في كل خطوة في الحالة السابقة مع بعض الاحتمالات \(p\)، ومع احتمال \(1-p\) نحن الانتقال إلى دولة مختلفة بشكل موحد وعشوائي. يتم أيضًا اختيار الحالة الأولية بشكل موحد عشوائيًا ، لذلك لدينا:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
هذه الافتراضات تتوافق إلى نموذج ماركوف المخفية مع انبعاثات بواسون. نحن يمكن ترميز لهم في TFP باستخدام tfd.HiddenMarkovModel . أولاً ، نحدد مصفوفة الانتقال والزي الرسمي السابق على الحالة الأولية:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
المقبل، ونحن بناء tfd.HiddenMarkovModel التوزيع، وذلك باستخدام متغير للتدريب لتمثيل معدلات المرتبطة بكل حالة النظام. نقوم بتحديد الأسعار في مساحة السجل للتأكد من أنها ذات قيمة إيجابية.
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
وأخيرا، فإننا تحديد إجمالي الكثافة السجل للنموذج، بما في ذلك اللوغاريتمي الطبيعي ضعيفة، بالمعلومات قبل على أسعار الفائدة، وتشغيل محسن لحساب الحد الأقصى لاحقة صالح (MAP) إلى بيانات العد الملحوظ.
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
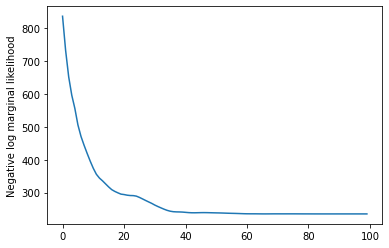
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
انها عملت! لاحظ أن الحالات الكامنة في هذا النموذج يمكن تحديدها حتى التبديل فقط ، لذا فإن المعدلات التي استعدناها تكون بترتيب مختلف ، وهناك القليل من الضوضاء ، لكنها تتطابق بشكل جيد بشكل عام.
استعادة مسار الدولة
الآن بعد أن قمنا تناسب نموذج، ونحن قد ترغب في إعادة بناء الدولة التي يعتقد النموذج كان النظام في في كل خطوة زمنية.
وهذه مهمة الاستدلال الخلفية: بالنظر إلى التهم المرصودة \(x_{1:T}\) والمعلمات نموذج (الرسوم) \(\lambda\)، ونحن نريد أن نستنتج تسلسل المتغيرات الكامنة منفصلة، في أعقاب الخلفي توزيع \(p(z_{1:T} | x_{1:T}, \lambda)\). في نموذج ماركوف المخفي ، يمكننا حساب الهامش والخصائص الأخرى لهذا التوزيع بكفاءة باستخدام خوارزميات قياسية لتمرير الرسائل. على وجه الخصوص، posterior_marginals وطريقة يحسبون بكفاءة (باستخدام خوارزمية إلى الأمام، الى الوراء ) وهامشية التوزيع الاحتمالي \(p(Z_t = z_t | x_{1:T})\) على منفصلة الكامنة الدولة \(Z_t\) في كل خطوة زمنية \(t\).
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
برسم الاحتمالات اللاحقة ، نستعيد "تفسير" النموذج للبيانات: في أي نقطة زمنية تكون كل حالة نشطة؟
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
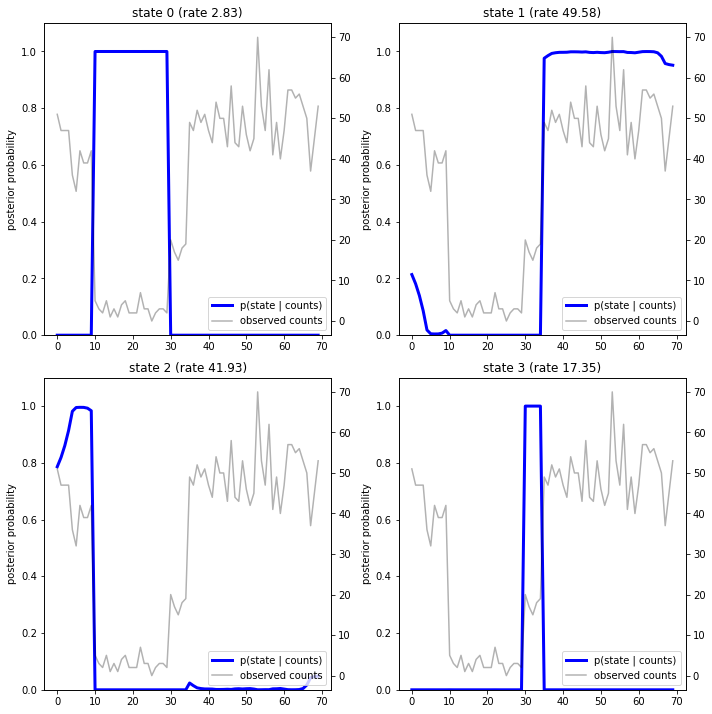
في هذه الحالة (البسيطة) ، نرى أن النموذج عادة ما يكون واثقًا تمامًا: في معظم الأوقات ، فإنه يخصص أساسًا كل كتلة الاحتمال إلى حالة واحدة من الحالات الأربع. لحسن الحظ ، تبدو التفسيرات معقولة!
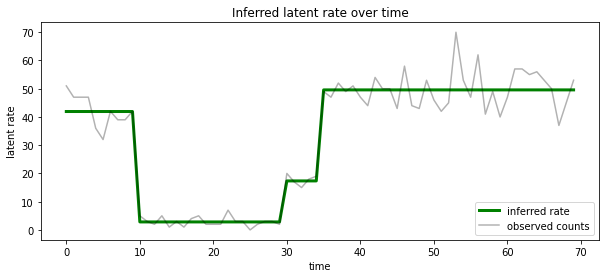
يمكننا أيضا أن تصور هذه الخلفية من حيث معدل المرتبطة معظم ولاية الكامنة المحتملة في كل خطوة زمنية، التكثيف الخلفي الاحتمالية في تفسير واحد:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
عدد غير معروف من الدول
في المشاكل الحقيقية ، قد لا نعرف العدد "الحقيقي" للحالات في النظام الذي نصممه. قد لا يكون هذا مصدر قلق دائمًا: إذا كنت لا تهتم بشكل خاص بهويات الحالات المجهولة ، فيمكنك فقط تشغيل نموذج به حالات أكثر مما تعرف أن النموذج سيحتاجه ، وتعلم (شيء مثل) مجموعة مكررة نسخ من الدول الفعلية. لكن لنفترض أنك تهتم باستنتاج العدد "الحقيقي" للحالات الكامنة.
يمكننا أن نرى في ذلك حالة النظرية الافتراضية اختيار نموذج : لدينا مجموعة من النماذج مرشح، ولكل منها عدد مختلف من الدول الكامنة، ونحن نريد لاختيار واحد هو الأكثر احتمالا أن ولدت البيانات المرصودة. للقيام بذلك، ونحن حساب احتمال هامشية من البيانات تحت كل نموذج (يمكننا أيضا إضافة قبل على نماذج أنفسهم، ولكن ذلك لن يكون من الضروري في هذا التحليل، و الحلاقة النظرية الافتراضية أوكام تبين أن تكون كافية لترميز ل تفضيل النماذج الأبسط).
وللأسف، فإن احتمال هامشية الحقيقي الذي يدمج على كل من الدول المنفصلة \(z_{1:T}\) و(ناقلات) معلمات معدل \(\lambda\)، \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) ليس لين العريكة لهذا النموذج. للراحة، وسنقوم تقريب ذلك باستخدام ما يسمى ب " بايز تجريبية " أو "النوع الثاني من أقصى احتمال" تقدير: بدلا من دمج تماما من المعلمات معدل (غير معروف) \(\lambda\) المرتبطة بكل حالة النظام، سنقوم تحسين على قيمهم:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
قد يكون هذا التقريب أكثر من اللازم ، أي أنه سيفضل نماذج أكثر تعقيدًا من الاحتمال الهامشي الحقيقي. يمكننا النظر تقريبية أكثر المؤمنين، على سبيل المثال، وتحسين والتغاير الأدنى، أو باستخدام مونت كارلو مقدر مثل أخذ العينات أهمية صلب . هذه (للأسف) خارج نطاق هذا دفتر الملاحظات. (لمعرفة المزيد عن النظرية الافتراضية اختيار نموذج وتقريبية، الفصل 7 من ممتاز آلة التعلم: منظور الاحتمالية هي إشارة جيدة.)
من حيث المبدأ، يمكننا أن نفعل هذه المقارنة نموذج ببساطة عن طريق إعادة تشغيل النص الأمثل فوق عدة مرات مع القيم المختلفة لل num_states ، لكن ذلك سيكون هناك الكثير من العمل. نحن هنا سوف تظهر كيفية نظر في نماذج متعددة في نفس الوقت، وذلك باستخدام TFP في batch_shape آلية لكمية موجهة.
مصفوفة الانتقال والحالة الأولية قبل: بدلا من بناء وصفا نموذج واحد، والآن سنقوم ببناء مجموعة من المصفوفات الانتقالية وlogits السابقة، واحد لكل نموذج مرشح حتى max_num_states . لسهولة التجميع ، سنحتاج إلى التأكد من أن جميع الحسابات لها نفس "الشكل": يجب أن يتوافق هذا مع أبعاد أكبر نموذج سنلائمه. للتعامل مع النماذج الأصغر ، يمكننا "تضمين" أوصافها في الأبعاد العليا لمساحة الحالة ، ومعالجة الأبعاد المتبقية بشكل فعال كحالات وهمية لا يتم استخدامها أبدًا.
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
الآن ننتقل بالمثل على النحو الوارد أعلاه. هذه المرة سنستخدم بعدا دفعة إضافية في trainable_rates لتناسب بشكل منفصل معدلات لكل نموذج قيد النظر.
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
عند حساب مشكلة السجل الإجمالي ، نحن حريصون على جمع المقدمات السابقة فقط للمعدلات المستخدمة بالفعل بواسطة كل مكون من مكونات النموذج:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
الآن نحن الأمثل الهدف دفعة لقد شيدت، وتركيب جميع النماذج مرشح في وقت واحد:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
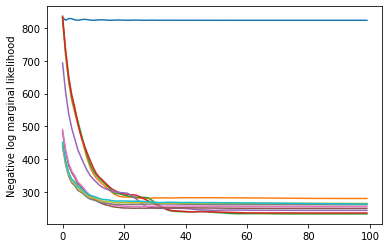
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
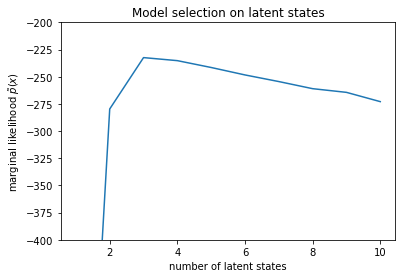
عند فحص الاحتمالات ، نرى أن الاحتمال الهامشي (التقريبي) يميل إلى تفضيل نموذج ثلاثي الحالات. يبدو هذا معقولًا تمامًا - النموذج "الحقيقي" يحتوي على أربع حالات ، ولكن بمجرد النظر إلى البيانات ، يصعب استبعاد تفسير ثلاثي الحالات.
يمكننا أيضًا استخراج المعدلات المناسبة لكل نموذج مرشح:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
وارسم التفسيرات التي يوفرها كل نموذج للبيانات:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
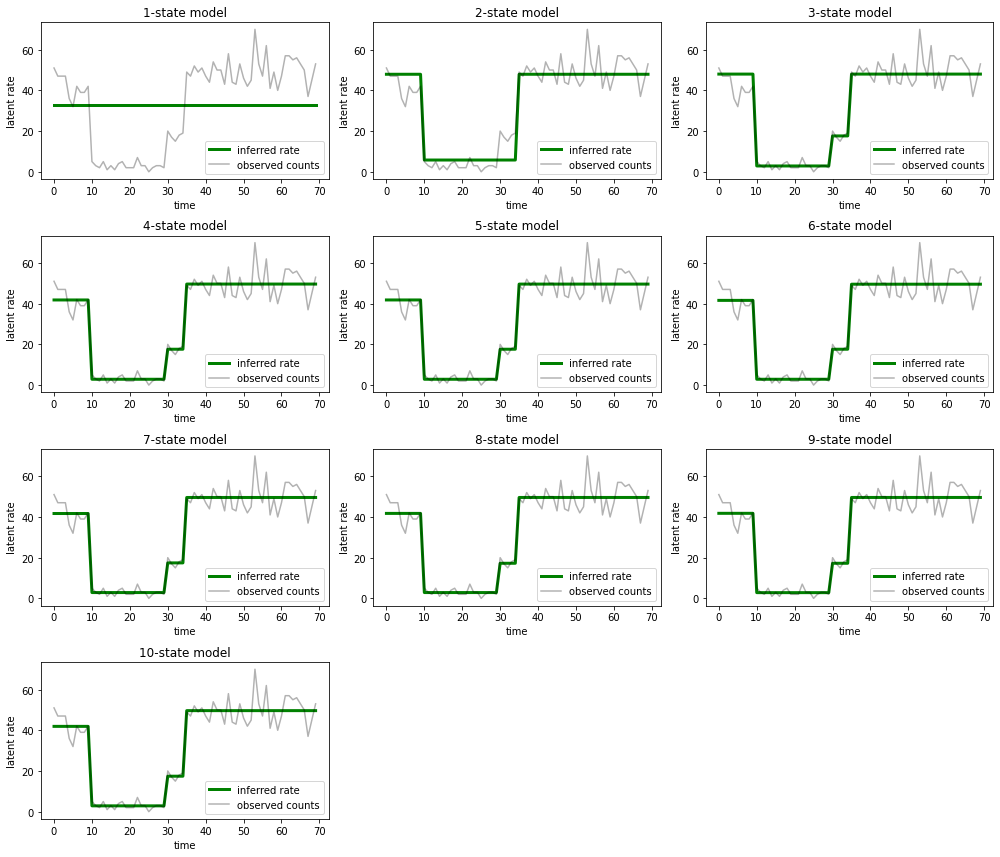
من السهل أن نرى كيف أن النماذج ذات الحالة الواحدة والثانية وثلاثية (بشكل أكثر دقة) تقدم تفسيرات غير كافية. ومن المثير للاهتمام أن جميع النماذج فوق أربع حالات تقدم أساسًا نفس التفسير! هذا على الأرجح لأن "بياناتنا" نظيفة نسبيًا ولا تترك مجالًا كبيرًا للتفسيرات البديلة ؛ بناءً على بيانات العالم الحقيقي messier ، نتوقع أن توفر النماذج ذات السعة الأعلى بشكل تدريجي أفضل ملاءمة للبيانات ، مع بعض نقاط المقايضة حيث يتم تجاوز الملاءمة المحسّنة من خلال تعقيد النموذج.
ملحقات
يمكن توسيع النماذج الموجودة في هذا الكمبيوتر المحمول بشكل مباشر بعدة طرق. فمثلا:
- السماح للحالات الكامنة بأن يكون لها احتمالات مختلفة (قد تكون بعض الحالات شائعة مقابل نادرة)
- السماح بالانتقالات غير المنتظمة بين الحالات الكامنة (على سبيل المثال ، لمعرفة أن تعطل الجهاز عادة ما يتبعه إعادة تشغيل النظام عادة ما يتبعه فترة من الأداء الجيد ، وما إلى ذلك)
- نماذج الانبعاثات الأخرى، على سبيل المثال
NegativeBinomialلنموذج التفرق في بيانات العد، أو توزيعات المستمر مختلفة مثلNormalللبيانات قيمتها الحقيقية.
