 Veja no TensorFlow.org Veja no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Como sempre, o código neste exemplo usará a API tf.keras , sobre a qual você pode saber mais no guia TensorFlow Keras .
Em ambos os exemplos anteriores - classificação de texto e previsão de eficiência de combustível - vimos que a precisão do nosso modelo nos dados de validação atingiria o pico após o treinamento por várias épocas e então estagnaria ou começaria a diminuir.
Em outras palavras, nosso modelo se ajustaria aos dados de treinamento. Aprender a lidar com o overfitting é importante. Embora muitas vezes seja possível obter alta precisão no conjunto de treinamento , o que realmente queremos é desenvolver modelos que generalizem bem para um conjunto de teste (ou dados que eles não viram antes).
O oposto de overfitting é underfitting . O underfitting ocorre quando ainda há espaço para melhorias nos dados do trem. Isso pode acontecer por vários motivos: se o modelo não for poderoso o suficiente, estiver excessivamente regularizado ou simplesmente não tiver sido treinado por tempo suficiente. Isso significa que a rede não aprendeu os padrões relevantes nos dados de treinamento.
No entanto, se você treinar por muito tempo, o modelo começará a se ajustar demais e aprenderá padrões dos dados de treinamento que não generalizam para os dados de teste. Precisamos encontrar um equilíbrio. Entender como treinar para um número apropriado de épocas, como exploraremos abaixo, é uma habilidade útil.
Para evitar o overfitting, a melhor solução é usar dados de treinamento mais completos. O conjunto de dados deve cobrir toda a gama de entradas que o modelo deve manipular. Dados adicionais só podem ser úteis se abrangerem casos novos e interessantes.
Um modelo treinado em dados mais completos naturalmente generalizará melhor. Quando isso não for mais possível, a próxima melhor solução é usar técnicas como a regularização. Isso impõe restrições à quantidade e ao tipo de informação que seu modelo pode armazenar. Se uma rede só puder memorizar um pequeno número de padrões, o processo de otimização a forçará a se concentrar nos padrões mais proeminentes, que têm mais chances de generalizar bem.
Neste caderno, exploraremos várias técnicas comuns de regularização e as usaremos para aprimorar um modelo de classificação.
Configurar
Antes de começar, importe os pacotes necessários:
import tensorflow as tf
from tensorflow.keras import layers
from tensorflow.keras import regularizers
print(tf.__version__)
2.8.0-rc1
!pip install git+https://github.com/tensorflow/docs
import tensorflow_docs as tfdocs
import tensorflow_docs.modeling
import tensorflow_docs.plots
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import pathlib
import shutil
import tempfile
logdir = pathlib.Path(tempfile.mkdtemp())/"tensorboard_logs"
shutil.rmtree(logdir, ignore_errors=True)
O conjunto de dados de Higgs
O objetivo deste tutorial não é fazer física de partículas, portanto, não se detenha nos detalhes do conjunto de dados. Ele contém 11.000.000 exemplos, cada um com 28 recursos e um rótulo de classe binária.
gz = tf.keras.utils.get_file('HIGGS.csv.gz', 'http://mlphysics.ics.uci.edu/data/higgs/HIGGS.csv.gz')
Downloading data from http://mlphysics.ics.uci.edu/data/higgs/HIGGS.csv.gz 2816409600/2816407858 [==============================] - 123s 0us/step 2816417792/2816407858 [==============================] - 123s 0us/step
FEATURES = 28
A classe tf.data.experimental.CsvDataset pode ser usada para ler registros csv diretamente de um arquivo gzip sem etapa de descompactação intermediária.
ds = tf.data.experimental.CsvDataset(gz,[float(),]*(FEATURES+1), compression_type="GZIP")
Essa classe de leitor de csv retorna uma lista de escalares para cada registro. A função a seguir reempacota essa lista de escalares em um par (feature_vector, label).
def pack_row(*row):
label = row[0]
features = tf.stack(row[1:],1)
return features, label
O TensorFlow é mais eficiente ao operar em grandes lotes de dados.
Portanto, em vez de reempacotar cada linha individualmente, crie um novo conjunto de Dataset que receba lotes de 10.000 exemplos, aplique a função pack_row a cada lote e, em seguida, divida os lotes em registros individuais:
packed_ds = ds.batch(10000).map(pack_row).unbatch()
Dê uma olhada em alguns dos registros deste novo packed_ds .
Os recursos não estão perfeitamente normalizados, mas isso é suficiente para este tutorial.
for features,label in packed_ds.batch(1000).take(1):
print(features[0])
plt.hist(features.numpy().flatten(), bins = 101)
tf.Tensor( [ 0.8692932 -0.6350818 0.22569026 0.32747006 -0.6899932 0.75420225 -0.24857314 -1.0920639 0. 1.3749921 -0.6536742 0.9303491 1.1074361 1.1389043 -1.5781983 -1.0469854 0. 0.65792954 -0.01045457 -0.04576717 3.1019614 1.35376 0.9795631 0.97807616 0.92000484 0.72165745 0.98875093 0.87667835], shape=(28,), dtype=float32)
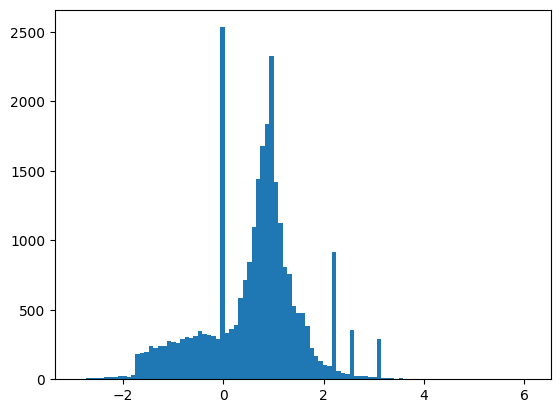
Para manter este tutorial relativamente curto, use apenas as primeiras 1.000 amostras para validação e as próximas 10.000 para treinamento:
N_VALIDATION = int(1e3)
N_TRAIN = int(1e4)
BUFFER_SIZE = int(1e4)
BATCH_SIZE = 500
STEPS_PER_EPOCH = N_TRAIN//BATCH_SIZE
Os métodos Dataset.skip e Dataset.take facilitam isso.
Ao mesmo tempo, use o método Dataset.cache para garantir que o carregador não precise reler os dados do arquivo em cada época:
validate_ds = packed_ds.take(N_VALIDATION).cache()
train_ds = packed_ds.skip(N_VALIDATION).take(N_TRAIN).cache()
train_ds
<CacheDataset element_spec=(TensorSpec(shape=(28,), dtype=tf.float32, name=None), TensorSpec(shape=(), dtype=tf.float32, name=None))>
Esses conjuntos de dados retornam exemplos individuais. Use o método .batch para criar lotes de tamanho apropriado para treinamento. Antes do batching, lembre-se de .shuffle e .repeat o conjunto de treinamento.
validate_ds = validate_ds.batch(BATCH_SIZE)
train_ds = train_ds.shuffle(BUFFER_SIZE).repeat().batch(BATCH_SIZE)
Demonstrar sobreajuste
A maneira mais simples de evitar o overfitting é começar com um modelo pequeno: um modelo com um pequeno número de parâmetros apreensíveis (que é determinado pelo número de camadas e o número de unidades por camada). No aprendizado profundo, o número de parâmetros que podem ser aprendidos em um modelo é geralmente chamado de "capacidade" do modelo.
Intuitivamente, um modelo com mais parâmetros terá mais "capacidade de memorização" e, portanto, poderá aprender facilmente um mapeamento perfeito do tipo dicionário entre amostras de treinamento e seus alvos, um mapeamento sem nenhum poder de generalização, mas isso seria inútil ao fazer previsões em dados inéditos.
Sempre tenha isso em mente: os modelos de aprendizado profundo tendem a ser bons em se ajustar aos dados de treinamento, mas o verdadeiro desafio é a generalização, não o ajuste.
Por outro lado, se a rede tiver recursos de memorização limitados, ela não conseguirá aprender o mapeamento com tanta facilidade. Para minimizar sua perda, ele terá que aprender representações compactadas que tenham mais poder preditivo. Ao mesmo tempo, se você tornar seu modelo muito pequeno, ele terá dificuldade em se ajustar aos dados de treinamento. Há um equilíbrio entre "capacidade demais" e "capacidade insuficiente".
Infelizmente, não existe uma fórmula mágica para determinar o tamanho certo ou a arquitetura do seu modelo (em termos de número de camadas ou o tamanho certo para cada camada). Você terá que experimentar usando uma série de arquiteturas diferentes.
Para encontrar um tamanho de modelo apropriado, é melhor começar com relativamente poucas camadas e parâmetros e, em seguida, começar a aumentar o tamanho das camadas ou adicionar novas camadas até ver retornos decrescentes na perda de validação.
Comece com um modelo simples usando apenas layers.Dense como linha de base, depois crie versões maiores e compare-as.
Procedimento de treinamento
Muitos modelos treinam melhor se você reduzir gradualmente a taxa de aprendizado durante o treinamento. Use optimizers.schedules para reduzir a taxa de aprendizado ao longo do tempo:
lr_schedule = tf.keras.optimizers.schedules.InverseTimeDecay(
0.001,
decay_steps=STEPS_PER_EPOCH*1000,
decay_rate=1,
staircase=False)
def get_optimizer():
return tf.keras.optimizers.Adam(lr_schedule)
O código acima define um schedules.InverseTimeDecay para diminuir hiperbolicamente a taxa de aprendizado para 1/2 da taxa básica em 1.000 épocas, 1/3 em 2.000 épocas e assim por diante.
step = np.linspace(0,100000)
lr = lr_schedule(step)
plt.figure(figsize = (8,6))
plt.plot(step/STEPS_PER_EPOCH, lr)
plt.ylim([0,max(plt.ylim())])
plt.xlabel('Epoch')
_ = plt.ylabel('Learning Rate')

Cada modelo neste tutorial usará a mesma configuração de treinamento. Portanto, configure-os de maneira reutilizável, começando com a lista de retornos de chamada.
O treinamento para este tutorial é executado por muitas épocas curtas. Para reduzir o ruído de log, use o tfdocs.EpochDots que simplesmente imprime um arquivo . para cada época e um conjunto completo de métricas a cada 100 épocas.
Em seguida, inclua callbacks.EarlyStopping para evitar tempos de treinamento longos e desnecessários. Observe que esse retorno de chamada é definido para monitorar o val_binary_crossentropy , não o val_loss . Essa diferença será importante mais tarde.
Use callbacks.TensorBoard para gerar logs do TensorBoard para o treinamento.
def get_callbacks(name):
return [
tfdocs.modeling.EpochDots(),
tf.keras.callbacks.EarlyStopping(monitor='val_binary_crossentropy', patience=200),
tf.keras.callbacks.TensorBoard(logdir/name),
]
Da mesma forma, cada modelo usará as mesmas configurações Model.compile e Model.fit :
def compile_and_fit(model, name, optimizer=None, max_epochs=10000):
if optimizer is None:
optimizer = get_optimizer()
model.compile(optimizer=optimizer,
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[
tf.keras.losses.BinaryCrossentropy(
from_logits=True, name='binary_crossentropy'),
'accuracy'])
model.summary()
history = model.fit(
train_ds,
steps_per_epoch = STEPS_PER_EPOCH,
epochs=max_epochs,
validation_data=validate_ds,
callbacks=get_callbacks(name),
verbose=0)
return history
Modelo minúsculo
Comece treinando um modelo:
tiny_model = tf.keras.Sequential([
layers.Dense(16, activation='elu', input_shape=(FEATURES,)),
layers.Dense(1)
])
size_histories = {}
size_histories['Tiny'] = compile_and_fit(tiny_model, 'sizes/Tiny')
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 16) 464
dense_1 (Dense) (None, 1) 17
=================================================================
Total params: 481
Trainable params: 481
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.4961, binary_crossentropy:0.7294, loss:0.7294, val_accuracy:0.4840, val_binary_crossentropy:0.7200, val_loss:0.7200,
....................................................................................................
Epoch: 100, accuracy:0.5931, binary_crossentropy:0.6279, loss:0.6279, val_accuracy:0.5860, val_binary_crossentropy:0.6288, val_loss:0.6288,
....................................................................................................
Epoch: 200, accuracy:0.6157, binary_crossentropy:0.6178, loss:0.6178, val_accuracy:0.6200, val_binary_crossentropy:0.6134, val_loss:0.6134,
....................................................................................................
Epoch: 300, accuracy:0.6370, binary_crossentropy:0.6086, loss:0.6086, val_accuracy:0.6220, val_binary_crossentropy:0.6055, val_loss:0.6055,
....................................................................................................
Epoch: 400, accuracy:0.6522, binary_crossentropy:0.6008, loss:0.6008, val_accuracy:0.6260, val_binary_crossentropy:0.5997, val_loss:0.5997,
....................................................................................................
Epoch: 500, accuracy:0.6513, binary_crossentropy:0.5946, loss:0.5946, val_accuracy:0.6480, val_binary_crossentropy:0.5911, val_loss:0.5911,
....................................................................................................
Epoch: 600, accuracy:0.6636, binary_crossentropy:0.5894, loss:0.5894, val_accuracy:0.6390, val_binary_crossentropy:0.5898, val_loss:0.5898,
....................................................................................................
Epoch: 700, accuracy:0.6696, binary_crossentropy:0.5852, loss:0.5852, val_accuracy:0.6530, val_binary_crossentropy:0.5870, val_loss:0.5870,
....................................................................................................
Epoch: 800, accuracy:0.6706, binary_crossentropy:0.5824, loss:0.5824, val_accuracy:0.6590, val_binary_crossentropy:0.5850, val_loss:0.5850,
....................................................................................................
Epoch: 900, accuracy:0.6709, binary_crossentropy:0.5796, loss:0.5796, val_accuracy:0.6680, val_binary_crossentropy:0.5831, val_loss:0.5831,
....................................................................................................
Epoch: 1000, accuracy:0.6780, binary_crossentropy:0.5769, loss:0.5769, val_accuracy:0.6530, val_binary_crossentropy:0.5851, val_loss:0.5851,
....................................................................................................
Epoch: 1100, accuracy:0.6735, binary_crossentropy:0.5752, loss:0.5752, val_accuracy:0.6620, val_binary_crossentropy:0.5807, val_loss:0.5807,
....................................................................................................
Epoch: 1200, accuracy:0.6759, binary_crossentropy:0.5729, loss:0.5729, val_accuracy:0.6620, val_binary_crossentropy:0.5792, val_loss:0.5792,
....................................................................................................
Epoch: 1300, accuracy:0.6849, binary_crossentropy:0.5716, loss:0.5716, val_accuracy:0.6450, val_binary_crossentropy:0.5859, val_loss:0.5859,
....................................................................................................
Epoch: 1400, accuracy:0.6790, binary_crossentropy:0.5695, loss:0.5695, val_accuracy:0.6700, val_binary_crossentropy:0.5776, val_loss:0.5776,
....................................................................................................
Epoch: 1500, accuracy:0.6824, binary_crossentropy:0.5681, loss:0.5681, val_accuracy:0.6730, val_binary_crossentropy:0.5761, val_loss:0.5761,
....................................................................................................
Epoch: 1600, accuracy:0.6828, binary_crossentropy:0.5669, loss:0.5669, val_accuracy:0.6690, val_binary_crossentropy:0.5766, val_loss:0.5766,
....................................................................................................
Epoch: 1700, accuracy:0.6874, binary_crossentropy:0.5657, loss:0.5657, val_accuracy:0.6600, val_binary_crossentropy:0.5774, val_loss:0.5774,
....................................................................................................
Epoch: 1800, accuracy:0.6845, binary_crossentropy:0.5655, loss:0.5655, val_accuracy:0.6780, val_binary_crossentropy:0.5752, val_loss:0.5752,
....................................................................................................
Epoch: 1900, accuracy:0.6837, binary_crossentropy:0.5644, loss:0.5644, val_accuracy:0.6790, val_binary_crossentropy:0.5753, val_loss:0.5753,
....................................................................................................
Epoch: 2000, accuracy:0.6853, binary_crossentropy:0.5632, loss:0.5632, val_accuracy:0.6780, val_binary_crossentropy:0.5753, val_loss:0.5753,
....................................................................................................
Epoch: 2100, accuracy:0.6871, binary_crossentropy:0.5625, loss:0.5625, val_accuracy:0.6670, val_binary_crossentropy:0.5769, val_loss:0.5769,
...................................
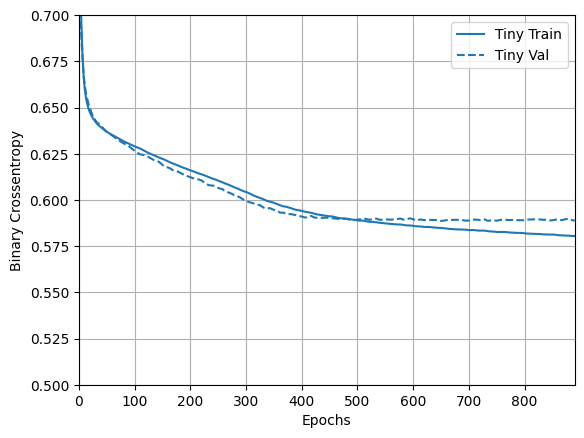
Agora confira como ficou o modelo:
plotter = tfdocs.plots.HistoryPlotter(metric = 'binary_crossentropy', smoothing_std=10)
plotter.plot(size_histories)
plt.ylim([0.5, 0.7])
(0.5, 0.7)
Modelo pequeno
Para ver se você consegue superar o desempenho do modelo pequeno, treine progressivamente alguns modelos maiores.
Experimente duas camadas ocultas com 16 unidades cada:
small_model = tf.keras.Sequential([
# `input_shape` is only required here so that `.summary` works.
layers.Dense(16, activation='elu', input_shape=(FEATURES,)),
layers.Dense(16, activation='elu'),
layers.Dense(1)
])
size_histories['Small'] = compile_and_fit(small_model, 'sizes/Small')
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_2 (Dense) (None, 16) 464
dense_3 (Dense) (None, 16) 272
dense_4 (Dense) (None, 1) 17
=================================================================
Total params: 753
Trainable params: 753
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.4864, binary_crossentropy:0.7769, loss:0.7769, val_accuracy:0.4930, val_binary_crossentropy:0.7211, val_loss:0.7211,
....................................................................................................
Epoch: 100, accuracy:0.6386, binary_crossentropy:0.6052, loss:0.6052, val_accuracy:0.6020, val_binary_crossentropy:0.6177, val_loss:0.6177,
....................................................................................................
Epoch: 200, accuracy:0.6697, binary_crossentropy:0.5829, loss:0.5829, val_accuracy:0.6310, val_binary_crossentropy:0.6018, val_loss:0.6018,
....................................................................................................
Epoch: 300, accuracy:0.6838, binary_crossentropy:0.5721, loss:0.5721, val_accuracy:0.6490, val_binary_crossentropy:0.5940, val_loss:0.5940,
....................................................................................................
Epoch: 400, accuracy:0.6911, binary_crossentropy:0.5656, loss:0.5656, val_accuracy:0.6430, val_binary_crossentropy:0.5985, val_loss:0.5985,
....................................................................................................
Epoch: 500, accuracy:0.6930, binary_crossentropy:0.5607, loss:0.5607, val_accuracy:0.6430, val_binary_crossentropy:0.6028, val_loss:0.6028,
.........................
Modelo médio
Agora tente 3 camadas ocultas com 64 unidades cada:
medium_model = tf.keras.Sequential([
layers.Dense(64, activation='elu', input_shape=(FEATURES,)),
layers.Dense(64, activation='elu'),
layers.Dense(64, activation='elu'),
layers.Dense(1)
])
E treine o modelo usando os mesmos dados:
size_histories['Medium'] = compile_and_fit(medium_model, "sizes/Medium")
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_5 (Dense) (None, 64) 1856
dense_6 (Dense) (None, 64) 4160
dense_7 (Dense) (None, 64) 4160
dense_8 (Dense) (None, 1) 65
=================================================================
Total params: 10,241
Trainable params: 10,241
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.5017, binary_crossentropy:0.6840, loss:0.6840, val_accuracy:0.4790, val_binary_crossentropy:0.6723, val_loss:0.6723,
....................................................................................................
Epoch: 100, accuracy:0.7173, binary_crossentropy:0.5221, loss:0.5221, val_accuracy:0.6470, val_binary_crossentropy:0.6111, val_loss:0.6111,
....................................................................................................
Epoch: 200, accuracy:0.7884, binary_crossentropy:0.4270, loss:0.4270, val_accuracy:0.6390, val_binary_crossentropy:0.7045, val_loss:0.7045,
..............................................................
Modelo grande
Como exercício, você pode criar um modelo ainda maior e ver a rapidez com que ele começa a se ajustar demais. Em seguida, vamos adicionar a este benchmark uma rede que tem muito mais capacidade, muito mais do que o problema justificaria:
large_model = tf.keras.Sequential([
layers.Dense(512, activation='elu', input_shape=(FEATURES,)),
layers.Dense(512, activation='elu'),
layers.Dense(512, activation='elu'),
layers.Dense(512, activation='elu'),
layers.Dense(1)
])
E, novamente, treine o modelo usando os mesmos dados:
size_histories['large'] = compile_and_fit(large_model, "sizes/large")
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_9 (Dense) (None, 512) 14848
dense_10 (Dense) (None, 512) 262656
dense_11 (Dense) (None, 512) 262656
dense_12 (Dense) (None, 512) 262656
dense_13 (Dense) (None, 1) 513
=================================================================
Total params: 803,329
Trainable params: 803,329
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.5145, binary_crossentropy:0.7740, loss:0.7740, val_accuracy:0.4980, val_binary_crossentropy:0.6793, val_loss:0.6793,
....................................................................................................
Epoch: 100, accuracy:1.0000, binary_crossentropy:0.0020, loss:0.0020, val_accuracy:0.6600, val_binary_crossentropy:1.8540, val_loss:1.8540,
....................................................................................................
Epoch: 200, accuracy:1.0000, binary_crossentropy:0.0001, loss:0.0001, val_accuracy:0.6560, val_binary_crossentropy:2.5293, val_loss:2.5293,
..........................
Plote as perdas de treinamento e validação
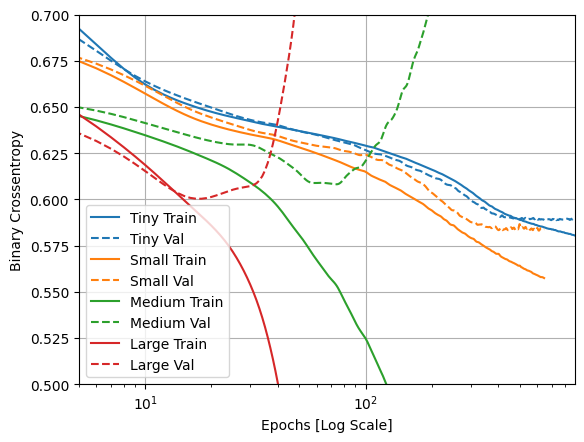
As linhas sólidas mostram a perda de treinamento e as linhas tracejadas mostram a perda de validação (lembre-se: uma perda de validação menor indica um modelo melhor).
Embora a construção de um modelo maior lhe dê mais poder, se esse poder não for restringido de alguma forma, ele pode facilmente se ajustar ao conjunto de treinamento.
Neste exemplo, normalmente, apenas o modelo "Tiny" consegue evitar completamente o overfitting, e cada um dos modelos maiores superajusta os dados mais rapidamente. Isso se torna tão grave para o modelo "large" que você precisa mudar o gráfico para uma escala logarítmica para realmente ver o que está acontecendo.
Isso fica aparente se você plotar e comparar as métricas de validação com as métricas de treinamento.
- É normal que haja uma pequena diferença.
- Se ambas as métricas estão se movendo na mesma direção, está tudo bem.
- Se a métrica de validação começar a estagnar enquanto a métrica de treinamento continua a melhorar, você provavelmente está perto do overfitting.
- Se a métrica de validação estiver indo na direção errada, o modelo está claramente superajustado.
plotter.plot(size_histories)
a = plt.xscale('log')
plt.xlim([5, max(plt.xlim())])
plt.ylim([0.5, 0.7])
plt.xlabel("Epochs [Log Scale]")
Text(0.5, 0, 'Epochs [Log Scale]')
Ver no TensorBoard
Todos esses modelos gravaram logs do TensorBoard durante o treinamento.
Abra um visualizador TensorBoard incorporado em um notebook:
#docs_infra: no_execute
# Load the TensorBoard notebook extension
%load_ext tensorboard
# Open an embedded TensorBoard viewer
%tensorboard --logdir {logdir}/sizes
Você pode ver os resultados de uma execução anterior deste notebook em TensorBoard.dev .
O TensorBoard.dev é uma experiência gerenciada para hospedar, rastrear e compartilhar experimentos de ML com todos.
Também está incluído em um <iframe> por conveniência:
display.IFrame(
src="https://tensorboard.dev/experiment/vW7jmmF9TmKmy3rbheMQpw/#scalars&_smoothingWeight=0.97",
width="100%", height="800px")
Se você quiser compartilhar os resultados do TensorBoard, faça upload dos logs para o TensorBoard.dev copiando o seguinte em uma célula de código.
tensorboard dev upload --logdir {logdir}/sizes
Estratégias para evitar o overfitting
Antes de entrar no conteúdo desta seção, copie os logs de treinamento do modelo "Tiny" acima, para usar como linha de base para comparação.
shutil.rmtree(logdir/'regularizers/Tiny', ignore_errors=True)
shutil.copytree(logdir/'sizes/Tiny', logdir/'regularizers/Tiny')
PosixPath('/tmp/tmpn1rdh98q/tensorboard_logs/regularizers/Tiny')
regularizer_histories = {}
regularizer_histories['Tiny'] = size_histories['Tiny']
Adicionar regularização de peso
Você pode estar familiarizado com o princípio da Navalha de Occam: dadas duas explicações para algo, a explicação mais provável de ser correta é a "mais simples", aquela que faz a menor quantidade de suposições. Isso também se aplica aos modelos aprendidos pelas redes neurais: dados alguns dados de treinamento e uma arquitetura de rede, existem vários conjuntos de valores de pesos (múltiplos modelos) que podem explicar os dados, e modelos mais simples são menos propensos a sobreajustar do que os complexos.
Um "modelo simples" neste contexto é um modelo onde a distribuição dos valores dos parâmetros tem menos entropia (ou um modelo com menos parâmetros, como vimos na seção acima). Assim, uma maneira comum de mitigar o overfitting é colocar restrições na complexidade de uma rede, forçando seus pesos apenas a assumir valores pequenos, o que torna a distribuição de valores de peso mais "regular". Isso é chamado de "regularização de peso", e é feito adicionando à função de perda da rede um custo associado a ter grandes pesos. Este custo vem em dois sabores:
Regularização L1 , onde o custo adicionado é proporcional ao valor absoluto dos coeficientes dos pesos (ou seja, ao que é chamado de "norma L1" dos pesos).
Regularização L2 , onde o custo adicionado é proporcional ao quadrado do valor dos coeficientes dos pesos (ou seja, ao que é chamado de quadrado da "norma L2" dos pesos). A regularização L2 também é chamada de decaimento de peso no contexto de redes neurais. Não deixe que o nome diferente o confunda: a redução de peso é matematicamente igual à regularização L2.
A regularização L1 empurra os pesos para exatamente zero, incentivando um modelo esparso. A regularização de L2 penalizará os parâmetros de pesos sem torná-los esparsos, já que a penalidade vai para zero para pesos pequenos - uma razão pela qual L2 é mais comum.
Em tf.keras , a regularização de peso é adicionada passando instâncias do regularizador de peso para camadas como argumentos de palavras-chave. Vamos adicionar a regularização de peso L2 agora.
l2_model = tf.keras.Sequential([
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001),
input_shape=(FEATURES,)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(1)
])
regularizer_histories['l2'] = compile_and_fit(l2_model, "regularizers/l2")
Model: "sequential_4"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_14 (Dense) (None, 512) 14848
dense_15 (Dense) (None, 512) 262656
dense_16 (Dense) (None, 512) 262656
dense_17 (Dense) (None, 512) 262656
dense_18 (Dense) (None, 1) 513
=================================================================
Total params: 803,329
Trainable params: 803,329
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.5126, binary_crossentropy:0.7481, loss:2.2415, val_accuracy:0.4950, val_binary_crossentropy:0.6707, val_loss:2.0653,
....................................................................................................
Epoch: 100, accuracy:0.6625, binary_crossentropy:0.5945, loss:0.6173, val_accuracy:0.6400, val_binary_crossentropy:0.5871, val_loss:0.6100,
....................................................................................................
Epoch: 200, accuracy:0.6690, binary_crossentropy:0.5864, loss:0.6079, val_accuracy:0.6650, val_binary_crossentropy:0.5856, val_loss:0.6076,
....................................................................................................
Epoch: 300, accuracy:0.6790, binary_crossentropy:0.5762, loss:0.5976, val_accuracy:0.6550, val_binary_crossentropy:0.5881, val_loss:0.6095,
....................................................................................................
Epoch: 400, accuracy:0.6843, binary_crossentropy:0.5697, loss:0.5920, val_accuracy:0.6650, val_binary_crossentropy:0.5878, val_loss:0.6101,
....................................................................................................
Epoch: 500, accuracy:0.6897, binary_crossentropy:0.5651, loss:0.5907, val_accuracy:0.6890, val_binary_crossentropy:0.5798, val_loss:0.6055,
....................................................................................................
Epoch: 600, accuracy:0.6945, binary_crossentropy:0.5610, loss:0.5864, val_accuracy:0.6820, val_binary_crossentropy:0.5772, val_loss:0.6026,
..........................................................
l2(0.001) significa que cada coeficiente na matriz de peso da camada adicionará 0.001 * weight_coefficient_value**2 à perda total da rede.
É por isso que estamos monitorando o binary_crossentropy diretamente. Porque não tem esse componente de regularização misturado.
Portanto, esse mesmo modelo "Large" com uma penalidade de regularização L2 tem um desempenho muito melhor:
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
(0.5, 0.7)
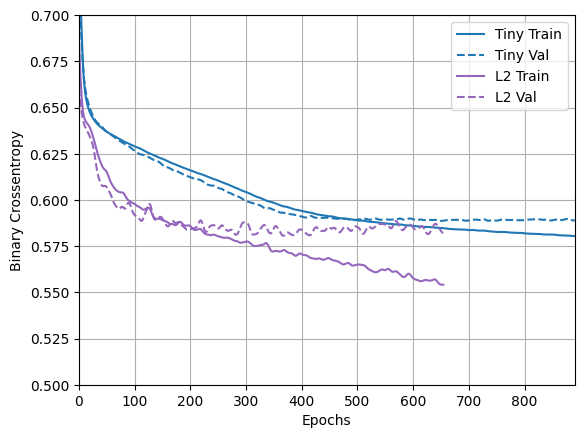
Como você pode ver, o modelo regularizado "L2" agora é muito mais competitivo com o modelo "Tiny" . Este modelo "L2" também é muito mais resistente ao overfitting do que o modelo "Large" em que foi baseado, apesar de ter o mesmo número de parâmetros.
Mais informações
Há duas coisas importantes a serem observadas sobre esse tipo de regularização.
Primeiro: se você estiver escrevendo seu próprio loop de treinamento, precisará perguntar ao modelo por suas perdas de regularização.
result = l2_model(features)
regularization_loss=tf.add_n(l2_model.losses)
Segundo: Esta implementação funciona adicionando as penalidades de peso à perda do modelo e, em seguida, aplicando um procedimento de otimização padrão depois disso.
Há uma segunda abordagem que, em vez disso, apenas executa o otimizador na perda bruta e, ao aplicar a etapa calculada, o otimizador também aplica alguma redução de peso. Este "Decoupled Weight Decay" é visto em otimizadores como optimizers.FTRL e optimizers.AdamW .
Adicionar desistência
Dropout é uma das técnicas de regularização mais eficazes e mais utilizadas para redes neurais, desenvolvida por Hinton e seus alunos da Universidade de Toronto.
A explicação intuitiva para o dropout é que, como os nós individuais na rede não podem contar com a saída dos outros, cada nó deve produzir recursos que sejam úteis por conta própria.
O dropout, aplicado a uma camada, consiste em "descartar" aleatoriamente (ou seja, definir como zero) um número de recursos de saída da camada durante o treinamento. Digamos que uma determinada camada normalmente retornaria um vetor [0,2, 0,5, 1,3, 0,8, 1,1] para uma determinada amostra de entrada durante o treinamento; após aplicar dropout, este vetor terá algumas entradas zero distribuídas aleatoriamente, por exemplo [0, 0,5, 1,3, 0, 1,1].
A "taxa de abandono" é a fração dos recursos que estão sendo zerados; geralmente é definido entre 0,2 e 0,5. No momento do teste, nenhuma unidade é descartada e, em vez disso, os valores de saída da camada são reduzidos por um fator igual à taxa de abandono, de modo a equilibrar o fato de que mais unidades estão ativas do que no tempo de treinamento.
Em tf.keras você pode introduzir dropout em uma rede através da camada Dropout, que é aplicada à saída da camada imediatamente anterior.
Vamos adicionar duas camadas Dropout em nossa rede para ver como elas se saem na redução do overfitting:
dropout_model = tf.keras.Sequential([
layers.Dense(512, activation='elu', input_shape=(FEATURES,)),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(1)
])
regularizer_histories['dropout'] = compile_and_fit(dropout_model, "regularizers/dropout")
Model: "sequential_5"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_19 (Dense) (None, 512) 14848
dropout (Dropout) (None, 512) 0
dense_20 (Dense) (None, 512) 262656
dropout_1 (Dropout) (None, 512) 0
dense_21 (Dense) (None, 512) 262656
dropout_2 (Dropout) (None, 512) 0
dense_22 (Dense) (None, 512) 262656
dropout_3 (Dropout) (None, 512) 0
dense_23 (Dense) (None, 1) 513
=================================================================
Total params: 803,329
Trainable params: 803,329
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.4961, binary_crossentropy:0.8110, loss:0.8110, val_accuracy:0.5330, val_binary_crossentropy:0.6900, val_loss:0.6900,
....................................................................................................
Epoch: 100, accuracy:0.6557, binary_crossentropy:0.5961, loss:0.5961, val_accuracy:0.6710, val_binary_crossentropy:0.5788, val_loss:0.5788,
....................................................................................................
Epoch: 200, accuracy:0.6871, binary_crossentropy:0.5622, loss:0.5622, val_accuracy:0.6860, val_binary_crossentropy:0.5856, val_loss:0.5856,
....................................................................................................
Epoch: 300, accuracy:0.7246, binary_crossentropy:0.5121, loss:0.5121, val_accuracy:0.6820, val_binary_crossentropy:0.5927, val_loss:0.5927,
............
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
(0.5, 0.7)
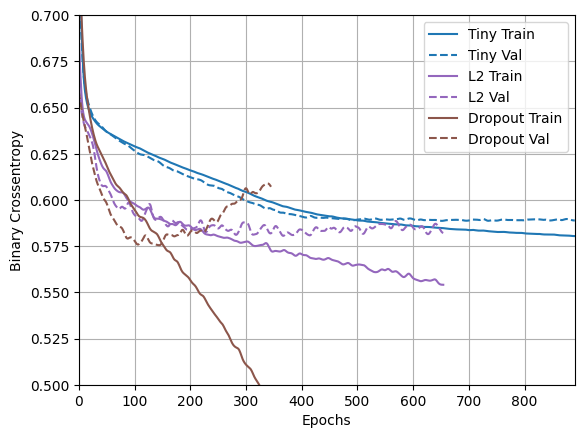
Fica claro neste gráfico que ambas as abordagens de regularização melhoram o comportamento do modelo "Large" . Mas isso ainda não supera nem a linha de base "Tiny" .
Em seguida, tente os dois, juntos, e veja se isso melhora.
L2 combinado + desistência
combined_model = tf.keras.Sequential([
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu', input_shape=(FEATURES,)),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(1)
])
regularizer_histories['combined'] = compile_and_fit(combined_model, "regularizers/combined")
Model: "sequential_6"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_24 (Dense) (None, 512) 14848
dropout_4 (Dropout) (None, 512) 0
dense_25 (Dense) (None, 512) 262656
dropout_5 (Dropout) (None, 512) 0
dense_26 (Dense) (None, 512) 262656
dropout_6 (Dropout) (None, 512) 0
dense_27 (Dense) (None, 512) 262656
dropout_7 (Dropout) (None, 512) 0
dense_28 (Dense) (None, 1) 513
=================================================================
Total params: 803,329
Trainable params: 803,329
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.5090, binary_crossentropy:0.8064, loss:0.9648, val_accuracy:0.4660, val_binary_crossentropy:0.6877, val_loss:0.8454,
....................................................................................................
Epoch: 100, accuracy:0.6445, binary_crossentropy:0.6050, loss:0.6350, val_accuracy:0.6630, val_binary_crossentropy:0.5871, val_loss:0.6169,
....................................................................................................
Epoch: 200, accuracy:0.6660, binary_crossentropy:0.5932, loss:0.6186, val_accuracy:0.6880, val_binary_crossentropy:0.5722, val_loss:0.5975,
....................................................................................................
Epoch: 300, accuracy:0.6697, binary_crossentropy:0.5818, loss:0.6100, val_accuracy:0.6900, val_binary_crossentropy:0.5614, val_loss:0.5895,
....................................................................................................
Epoch: 400, accuracy:0.6749, binary_crossentropy:0.5742, loss:0.6046, val_accuracy:0.6870, val_binary_crossentropy:0.5576, val_loss:0.5881,
....................................................................................................
Epoch: 500, accuracy:0.6854, binary_crossentropy:0.5703, loss:0.6029, val_accuracy:0.6970, val_binary_crossentropy:0.5458, val_loss:0.5784,
....................................................................................................
Epoch: 600, accuracy:0.6806, binary_crossentropy:0.5673, loss:0.6015, val_accuracy:0.6980, val_binary_crossentropy:0.5453, val_loss:0.5795,
....................................................................................................
Epoch: 700, accuracy:0.6937, binary_crossentropy:0.5583, loss:0.5938, val_accuracy:0.6870, val_binary_crossentropy:0.5477, val_loss:0.5832,
....................................................................................................
Epoch: 800, accuracy:0.6911, binary_crossentropy:0.5576, loss:0.5947, val_accuracy:0.7000, val_binary_crossentropy:0.5446, val_loss:0.5817,
.......................
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
(0.5, 0.7)
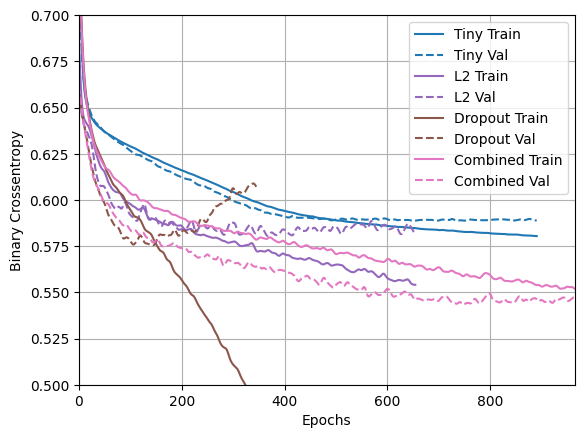
Este modelo com a regularização "Combined" é obviamente o melhor até agora.
Ver no TensorBoard
Esses modelos também registraram logs do TensorBoard.
Para abrir um visualizador de tensorboard incorporado em um notebook, copie o seguinte em uma célula de código:
%tensorboard --logdir {logdir}/regularizers
Você pode ver os resultados de uma execução anterior deste notebook em TensorDoard.dev .
Também está incluído em um <iframe> por conveniência:
display.IFrame(
src="https://tensorboard.dev/experiment/fGInKDo8TXes1z7HQku9mw/#scalars&_smoothingWeight=0.97",
width = "100%",
height="800px")
Isso foi carregado com:
tensorboard dev upload --logdir {logdir}/regularizers
Conclusões
Para recapitular: aqui estão as maneiras mais comuns de evitar o overfitting em redes neurais:
- Obtenha mais dados de treinamento.
- Reduza a capacidade da rede.
- Adicione regularização de peso.
- Adicionar desistência.
Duas abordagens importantes não abordadas neste guia são:
- aumento de dados
- normalização de lote
Lembre-se de que cada método pode ajudar sozinho, mas muitas vezes combiná-los pode ser ainda mais eficaz.
# MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.

