 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看 |
 在 Google Colab 中运行 在 Google Colab 中运行 |
 在 GitHub 上查看源代码 在 GitHub 上查看源代码 |
 下载笔记本 下载笔记本 |
本教程演示了如何对高度不平衡的数据集进行分类,在此类数据集中,一类中的样本数量远多于另一类中的样本数量。您将使用 Kaggle 上托管的 Credit Card Fraud Detection 数据集,目的是从总共 284,807 笔交易中检测出仅有的 492 笔欺诈交易。您将使用 Keras 来定义模型和类权重,从而帮助模型从不平衡数据中学习。
本教程包含下列操作的完整代码:
- 使用 Pandas 加载 CSV 文件。
- 创建训练、验证和测试集。
- 使用 Keras 定义并训练模型(包括设置类权重)。
- 使用各种指标(包括精确率和召回率)评估模型。
- 尝试使用常见技术来处理不平衡数据,例如:
- 类加权
- 过采样
设置
import tensorflow as tf
from tensorflow import keras
import os
import tempfile
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import sklearn
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
2023-11-08 01:16:05.391090: E external/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:9261] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2023-11-08 01:16:05.391146: E external/local_xla/xla/stream_executor/cuda/cuda_fft.cc:607] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2023-11-08 01:16:05.392950: E external/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1515] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered
mpl.rcParams['figure.figsize'] = (12, 10)
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
数据处理与浏览
下载 Kaggle Credit Card Fraud 数据集
Pandas 是一个 Python 库,其中包含许多有用的实用工具,用于加载和使用结构化数据,并可用于将 CSV 下载到数据帧中。
注:Worldline 和 ULB(布鲁塞尔自由大学)机器学习小组在大数据挖掘和欺诈检测的合作研究期间,已对此数据集进行了收集和分析。与相关主题当前和过去项目有关的详细信息,请访问这里和 DefeatFraud 项目页面。
file = tf.keras.utils
raw_df = pd.read_csv('https://storage.googleapis.com/download.tensorflow.org/data/creditcard.csv')
raw_df.head()
raw_df[['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V26', 'V27', 'V28', 'Amount', 'Class']].describe()
检查类标签的不平衡
让我们看一下数据集的不平衡情况:
neg, pos = np.bincount(raw_df['Class'])
total = neg + pos
print('Examples:\n Total: {}\n Positive: {} ({:.2f}% of total)\n'.format(
total, pos, 100 * pos / total))
Examples:
Total: 284807
Positive: 492 (0.17% of total)
这表明正样本的比例很小。
清理、拆分和归一化数据
原始数据有一些问题。首先,Time 和 Amount 列变化太大,无法直接使用。删除 Time 列(因为不清楚其含义),并获取 Amount 列的日志以缩小其范围。
cleaned_df = raw_df.copy()
# You don't want the `Time` column.
cleaned_df.pop('Time')
# The `Amount` column covers a huge range. Convert to log-space.
eps = 0.001 # 0 => 0.1¢
cleaned_df['Log Amount'] = np.log(cleaned_df.pop('Amount')+eps)
将数据集拆分为训练、验证和测试集。验证集在模型拟合期间使用,用于评估损失和任何指标,判断模型与数据的拟合程度。测试集在训练阶段完全不使用,仅在最后用于评估模型泛化到新数据的能力。这对于不平衡的数据集尤为重要,因为过拟合是缺乏训练数据造成的一个重大问题。
# Use a utility from sklearn to split and shuffle your dataset.
train_df, test_df = train_test_split(cleaned_df, test_size=0.2)
train_df, val_df = train_test_split(train_df, test_size=0.2)
# Form np arrays of labels and features.
train_labels = np.array(train_df.pop('Class'))
bool_train_labels = train_labels != 0
val_labels = np.array(val_df.pop('Class'))
test_labels = np.array(test_df.pop('Class'))
train_features = np.array(train_df)
val_features = np.array(val_df)
test_features = np.array(test_df)
使用 sklearn StandardScaler 将输入特征归一化。这会将平均值设置为 0,标准偏差设置为 1。
注:StandardScaler 只能使用 train_features 进行拟合,以确保模型不会窥视验证集或测试集。
scaler = StandardScaler()
train_features = scaler.fit_transform(train_features)
val_features = scaler.transform(val_features)
test_features = scaler.transform(test_features)
train_features = np.clip(train_features, -5, 5)
val_features = np.clip(val_features, -5, 5)
test_features = np.clip(test_features, -5, 5)
print('Training labels shape:', train_labels.shape)
print('Validation labels shape:', val_labels.shape)
print('Test labels shape:', test_labels.shape)
print('Training features shape:', train_features.shape)
print('Validation features shape:', val_features.shape)
print('Test features shape:', test_features.shape)
Training labels shape: (182276,) Validation labels shape: (45569,) Test labels shape: (56962,) Training features shape: (182276, 29) Validation features shape: (45569, 29) Test features shape: (56962, 29)
小心:如果要部署模型,保留预处理计算至关重要。这是将它们实现为层并在导出之前将它们附加到模型最简单的方法。
查看数据分布
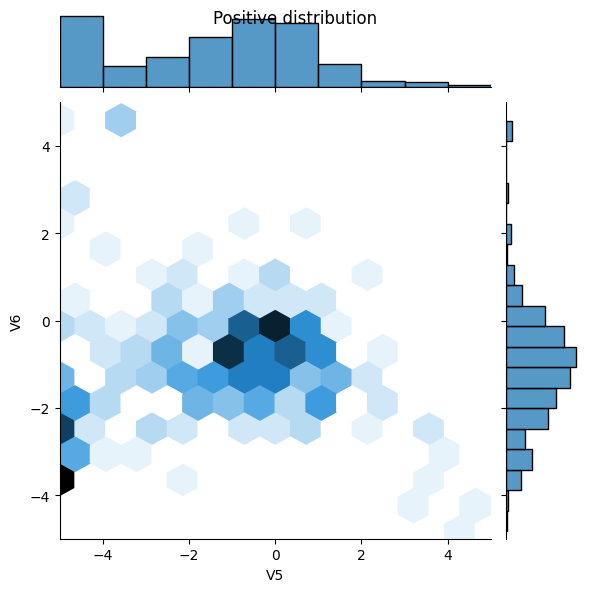
接下来通过一些特征比较一下正样本和负样本的分布。此时,建议您问自己如下问题:
- 这些分布是否有意义?
- 是。您已对输入进行了归一化处理,而它们大多集中在
+/- 2范围内。
- 是。您已对输入进行了归一化处理,而它们大多集中在
- 您是否能看出分布之间的差异?
- 是。正样本包含极值的比率高得多 。
pos_df = pd.DataFrame(train_features[ bool_train_labels], columns=train_df.columns)
neg_df = pd.DataFrame(train_features[~bool_train_labels], columns=train_df.columns)
sns.jointplot(x=pos_df['V5'], y=pos_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
plt.suptitle("Positive distribution")
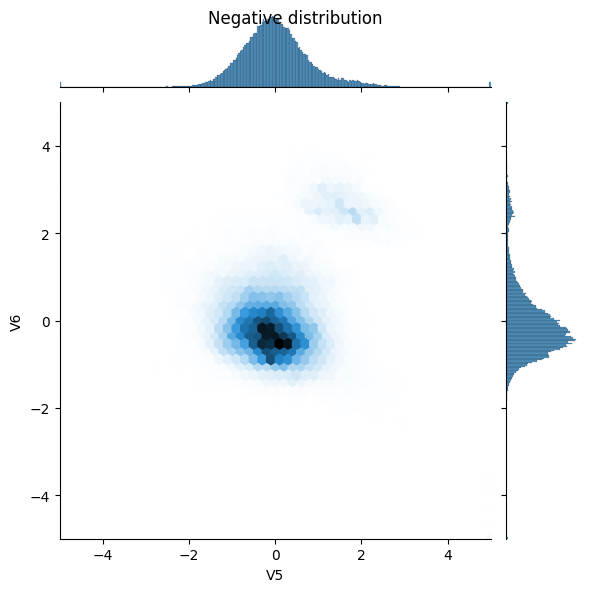
sns.jointplot(x=neg_df['V5'], y=neg_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
_ = plt.suptitle("Negative distribution")
定义模型和指标
定义一个函数,该函数会创建一个简单的神经网络,其中包含一个密集连接的隐藏层、一个用于减少过拟合的随机失活层,以及一个返回欺诈交易概率的输出 Sigmoid 层:
METRICS = [
keras.metrics.TruePositives(name='tp'),
keras.metrics.FalsePositives(name='fp'),
keras.metrics.TrueNegatives(name='tn'),
keras.metrics.FalseNegatives(name='fn'),
keras.metrics.BinaryAccuracy(name='accuracy'),
keras.metrics.Precision(name='precision'),
keras.metrics.Recall(name='recall'),
keras.metrics.AUC(name='auc'),
keras.metrics.AUC(name='prc', curve='PR'), # precision-recall curve
]
def make_model(metrics=METRICS, output_bias=None):
if output_bias is not None:
output_bias = tf.keras.initializers.Constant(output_bias)
model = keras.Sequential([
keras.layers.Dense(
16, activation='relu',
input_shape=(train_features.shape[-1],)),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation='sigmoid',
bias_initializer=output_bias),
])
model.compile(
optimizer=keras.optimizers.Adam(learning_rate=1e-3),
loss=keras.losses.BinaryCrossentropy(),
metrics=metrics)
return model
了解有用的指标
请注意,上面定义的一些指标可以由模型计算得出,这对评估性能很有帮助。
- 假负例和假正例是被错误分类的样本
- 真负例和真正例是被正确分类的样本
- 准确率是被正确分类的样本的百分比
\(\frac{\text{true samples} }{\text{total samples} }\)
- 精确率是被正确分类的预测正例的百分比
\(\frac{\text{true positives} }{\text{true positives + false positives} }\)
- 召回率是被正确分类的实际正例的百分比
\(\frac{\text{true positives} }{\text{true positives + false negatives} }\)
- AUC 是指接收器操作特征曲线中的曲线下方面积 (ROC-AUC)。此指标等于分类器对随机正样本的排序高于随机负样本的概率。
- AUPRC 是指精确率-召回率曲线下方面积。该指标计算不同概率阈值的精度率-召回率对。
注:准确率在此任务中不是一个有用的指标。只要始终预测“False”,您就可以在此任务中达到 99.8%+ 的准确率。
延伸阅读:
基线模型
构建模型
现在,使用先前定义的函数创建并训练模型。请注意,该模型使用大于默认的批次大小 (2048) 来进行拟合,这一点很重要,有助于确保每个批次都有一定机会包含少量正样本。如果批次过小,它们可能会没有可供学习的欺诈交易。
注:此模型无法很好地处理类不平衡问题。我们将在本教程的后面部分对此进行改进。
EPOCHS = 100
BATCH_SIZE = 2048
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor='val_auc',
verbose=1,
patience=10,
mode='max',
restore_best_weights=True)
model = make_model()
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 16) 480
dropout (Dropout) (None, 16) 0
dense_1 (Dense) (None, 1) 17
=================================================================
Total params: 497 (1.94 KB)
Trainable params: 497 (1.94 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________
试运行模型:
model.predict(train_features[:10])
1/1 [==============================] - 0s 377ms/step
array([[0.12993479],
[0.0831413 ],
[0.24497728],
[0.3017688 ],
[0.33697775],
[0.0949156 ],
[0.1872398 ],
[0.27218476],
[0.29461417],
[0.6366021 ]], dtype=float32)
可选:设置正确的初始偏差。
模型最初的猜测不太理想。您知道数据集不平衡,因此需要设置输出层的偏差以反映这种不平衡(请参阅:训练神经网络的秘诀:“好好初始化”)。这样做有助于初始收敛。
使用默认偏差初始化时,损失应约为 math.log(2) = 0.69314。
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 0.3724
可以用以下代码推导出要设置的正确偏差:
\( p_0 = pos/(pos + neg) = 1/(1+e^{-b_0}) \) \( b_0 = -log_e(1/p_0 - 1) \) \[ b_0 = log_e(pos/neg)\]
initial_bias = np.log([pos/neg])
initial_bias
array([-6.35935934])
将其设置为初始偏差,模型将给出合理得多的初始猜测。
结果应该接近:pos/total = 0.0018
model = make_model(output_bias = initial_bias)
model.predict(train_features[:10])
1/1 [==============================] - 0s 81ms/step
array([[0.00022771],
[0.00144273],
[0.00385517],
[0.00052363],
[0.00052137],
[0.00077223],
[0.00100834],
[0.00055533],
[0.00064206],
[0.00016787]], dtype=float32)
使用此初始化,初始损失应约为:
\[-p_0log(p_0)-(1-p_0)log(1-p_0) = 0.01317\]
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
Loss: 0.0174
此初始损失大约是使用朴素初始化时损失的 50 倍。
这样,模型就不需要花费前几个周期去仅仅了解不可能有正样本。这也使得在训练过程中更容易读取损失图。
为初始权重设置检查点
为了使各种训练运行更具可比性,请将这个初始模型的权重保存在检查点文件中,并在训练前将它们加载到每个模型中:
initial_weights = os.path.join(tempfile.mkdtemp(),'initial_weights')
model.save_weights(initial_weights)
确认偏差修正有帮助
在继续之前,迅速确认这一细致偏差初始化是否确实起了作用。
在使用和不使用此细致初始化的情况下,将模型训练 20 个周期,并比较损失:
model = make_model()
model.load_weights(initial_weights)
model.layers[-1].bias.assign([0.0])
zero_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
WARNING: All log messages before absl::InitializeLog() is called are written to STDERR I0000 00:00:1699406183.892374 943342 device_compiler.h:186] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process.
model = make_model()
model.load_weights(initial_weights)
careful_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
def plot_loss(history, label, n):
# Use a log scale to show the wide range of values.
plt.semilogy(history.epoch, history.history['loss'],
color=colors[n], label='Train '+label)
plt.semilogy(history.epoch, history.history['val_loss'],
color=colors[n], label='Val '+label,
linestyle="--")
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plot_loss(zero_bias_history, "Zero Bias", 0)
plot_loss(careful_bias_history, "Careful Bias", 1)

上图清楚表明:就验证损失而言,在这个问题上,此细致初始化具有明显优势。
训练模型
model = make_model()
model.load_weights(initial_weights)
baseline_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks = [early_stopping],
validation_data=(val_features, val_labels))
Epoch 1/100 90/90 [==============================] - 3s 12ms/step - loss: 0.0135 - tp: 101.0000 - fp: 26.0000 - tn: 227434.0000 - fn: 284.0000 - accuracy: 0.9986 - precision: 0.7953 - recall: 0.2623 - auc: 0.7220 - prc: 0.3198 - val_loss: 0.0076 - val_tp: 3.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 66.0000 - val_accuracy: 0.9984 - val_precision: 0.3750 - val_recall: 0.0435 - val_auc: 0.8258 - val_prc: 0.4747 Epoch 2/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0094 - tp: 98.0000 - fp: 16.0000 - tn: 181944.0000 - fn: 218.0000 - accuracy: 0.9987 - precision: 0.8596 - recall: 0.3101 - auc: 0.7451 - prc: 0.3475 - val_loss: 0.0050 - val_tp: 18.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 51.0000 - val_accuracy: 0.9987 - val_precision: 0.7500 - val_recall: 0.2609 - val_auc: 0.9127 - val_prc: 0.6222 Epoch 3/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0079 - tp: 118.0000 - fp: 25.0000 - tn: 181935.0000 - fn: 198.0000 - accuracy: 0.9988 - precision: 0.8252 - recall: 0.3734 - auc: 0.8315 - prc: 0.4644 - val_loss: 0.0039 - val_tp: 38.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 31.0000 - val_accuracy: 0.9992 - val_precision: 0.8636 - val_recall: 0.5507 - val_auc: 0.9199 - val_prc: 0.6663 Epoch 4/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0069 - tp: 132.0000 - fp: 25.0000 - tn: 181935.0000 - fn: 184.0000 - accuracy: 0.9989 - precision: 0.8408 - recall: 0.4177 - auc: 0.8565 - prc: 0.5263 - val_loss: 0.0036 - val_tp: 43.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 26.0000 - val_accuracy: 0.9993 - val_precision: 0.8776 - val_recall: 0.6232 - val_auc: 0.9272 - val_prc: 0.6980 Epoch 5/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0065 - tp: 138.0000 - fp: 28.0000 - tn: 181932.0000 - fn: 178.0000 - accuracy: 0.9989 - precision: 0.8313 - recall: 0.4367 - auc: 0.8619 - prc: 0.5629 - val_loss: 0.0034 - val_tp: 44.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8800 - val_recall: 0.6377 - val_auc: 0.9345 - val_prc: 0.7071 Epoch 6/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0061 - tp: 149.0000 - fp: 29.0000 - tn: 181931.0000 - fn: 167.0000 - accuracy: 0.9989 - precision: 0.8371 - recall: 0.4715 - auc: 0.8767 - prc: 0.5928 - val_loss: 0.0032 - val_tp: 44.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8800 - val_recall: 0.6377 - val_auc: 0.9417 - val_prc: 0.7401 Epoch 7/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0061 - tp: 150.0000 - fp: 29.0000 - tn: 181931.0000 - fn: 166.0000 - accuracy: 0.9989 - precision: 0.8380 - recall: 0.4747 - auc: 0.8655 - prc: 0.5760 - val_loss: 0.0031 - val_tp: 44.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 25.0000 - val_accuracy: 0.9993 - val_precision: 0.8800 - val_recall: 0.6377 - val_auc: 0.9418 - val_prc: 0.7652 Epoch 8/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0061 - tp: 144.0000 - fp: 22.0000 - tn: 181938.0000 - fn: 172.0000 - accuracy: 0.9989 - precision: 0.8675 - recall: 0.4557 - auc: 0.8658 - prc: 0.5889 - val_loss: 0.0029 - val_tp: 45.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6522 - val_auc: 0.9418 - val_prc: 0.7871 Epoch 9/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0059 - tp: 144.0000 - fp: 26.0000 - tn: 181934.0000 - fn: 172.0000 - accuracy: 0.9989 - precision: 0.8471 - recall: 0.4557 - auc: 0.8610 - prc: 0.5845 - val_loss: 0.0028 - val_tp: 46.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 23.0000 - val_accuracy: 0.9994 - val_precision: 0.8846 - val_recall: 0.6667 - val_auc: 0.9490 - val_prc: 0.8028 Epoch 10/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0058 - tp: 144.0000 - fp: 28.0000 - tn: 181932.0000 - fn: 172.0000 - accuracy: 0.9989 - precision: 0.8372 - recall: 0.4557 - auc: 0.8690 - prc: 0.5951 - val_loss: 0.0027 - val_tp: 45.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6522 - val_auc: 0.9490 - val_prc: 0.8107 Epoch 11/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0058 - tp: 150.0000 - fp: 24.0000 - tn: 181936.0000 - fn: 166.0000 - accuracy: 0.9990 - precision: 0.8621 - recall: 0.4747 - auc: 0.8626 - prc: 0.5828 - val_loss: 0.0027 - val_tp: 45.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 24.0000 - val_accuracy: 0.9993 - val_precision: 0.8824 - val_recall: 0.6522 - val_auc: 0.9491 - val_prc: 0.8156 Epoch 12/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0053 - tp: 154.0000 - fp: 26.0000 - tn: 181934.0000 - fn: 162.0000 - accuracy: 0.9990 - precision: 0.8556 - recall: 0.4873 - auc: 0.8739 - prc: 0.6229 - val_loss: 0.0026 - val_tp: 48.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 21.0000 - val_accuracy: 0.9994 - val_precision: 0.8889 - val_recall: 0.6957 - val_auc: 0.9563 - val_prc: 0.8279 Epoch 13/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0056 - tp: 142.0000 - fp: 28.0000 - tn: 181932.0000 - fn: 174.0000 - accuracy: 0.9989 - precision: 0.8353 - recall: 0.4494 - auc: 0.8627 - prc: 0.5919 - val_loss: 0.0025 - val_tp: 49.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 20.0000 - val_accuracy: 0.9994 - val_precision: 0.8750 - val_recall: 0.7101 - val_auc: 0.9563 - val_prc: 0.8343 Epoch 14/100 90/90 [==============================] - 0s 6ms/step - loss: 0.0054 - tp: 155.0000 - fp: 25.0000 - tn: 181935.0000 - fn: 161.0000 - accuracy: 0.9990 - precision: 0.8611 - recall: 0.4905 - auc: 0.8752 - prc: 0.6058 - val_loss: 0.0024 - val_tp: 51.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 18.0000 - val_accuracy: 0.9994 - val_precision: 0.8644 - val_recall: 0.7391 - val_auc: 0.9563 - val_prc: 0.8385 Epoch 15/100 90/90 [==============================] - 0s 6ms/step - loss: 0.0054 - tp: 160.0000 - fp: 30.0000 - tn: 181930.0000 - fn: 156.0000 - accuracy: 0.9990 - precision: 0.8421 - recall: 0.5063 - auc: 0.8722 - prc: 0.6190 - val_loss: 0.0024 - val_tp: 50.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8772 - val_recall: 0.7246 - val_auc: 0.9563 - val_prc: 0.8455 Epoch 16/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0053 - tp: 155.0000 - fp: 29.0000 - tn: 181931.0000 - fn: 161.0000 - accuracy: 0.9990 - precision: 0.8424 - recall: 0.4905 - auc: 0.8787 - prc: 0.6159 - val_loss: 0.0023 - val_tp: 50.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8772 - val_recall: 0.7246 - val_auc: 0.9563 - val_prc: 0.8522 Epoch 17/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0052 - tp: 172.0000 - fp: 35.0000 - tn: 181925.0000 - fn: 144.0000 - accuracy: 0.9990 - precision: 0.8309 - recall: 0.5443 - auc: 0.8802 - prc: 0.6151 - val_loss: 0.0023 - val_tp: 47.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 22.0000 - val_accuracy: 0.9994 - val_precision: 0.8868 - val_recall: 0.6812 - val_auc: 0.9563 - val_prc: 0.8593 Epoch 18/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0055 - tp: 138.0000 - fp: 26.0000 - tn: 181934.0000 - fn: 178.0000 - accuracy: 0.9989 - precision: 0.8415 - recall: 0.4367 - auc: 0.8657 - prc: 0.5980 - val_loss: 0.0022 - val_tp: 50.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8772 - val_recall: 0.7246 - val_auc: 0.9563 - val_prc: 0.8602 Epoch 19/100 90/90 [==============================] - 0s 5ms/step - loss: 0.0055 - tp: 149.0000 - fp: 26.0000 - tn: 181934.0000 - fn: 167.0000 - accuracy: 0.9989 - precision: 0.8514 - recall: 0.4715 - auc: 0.8546 - prc: 0.5791 - val_loss: 0.0022 - val_tp: 50.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8772 - val_recall: 0.7246 - val_auc: 0.9563 - val_prc: 0.8629 Epoch 20/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0053 - tp: 147.0000 - fp: 30.0000 - tn: 181930.0000 - fn: 169.0000 - accuracy: 0.9989 - precision: 0.8305 - recall: 0.4652 - auc: 0.8752 - prc: 0.6042 - val_loss: 0.0021 - val_tp: 50.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 19.0000 - val_accuracy: 0.9994 - val_precision: 0.8772 - val_recall: 0.7246 - val_auc: 0.9563 - val_prc: 0.8668 Epoch 21/100 90/90 [==============================] - 0s 6ms/step - loss: 0.0049 - tp: 164.0000 - fp: 21.0000 - tn: 181939.0000 - fn: 152.0000 - accuracy: 0.9991 - precision: 0.8865 - recall: 0.5190 - auc: 0.8737 - prc: 0.6472 - val_loss: 0.0021 - val_tp: 52.0000 - val_fp: 7.0000 - val_tn: 45493.0000 - val_fn: 17.0000 - val_accuracy: 0.9995 - val_precision: 0.8814 - val_recall: 0.7536 - val_auc: 0.9563 - val_prc: 0.8674 Epoch 22/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0050 - tp: 152.0000 - fp: 31.0000 - tn: 181929.0000 - fn: 164.0000 - accuracy: 0.9989 - precision: 0.8306 - recall: 0.4810 - auc: 0.8848 - prc: 0.6228 - val_loss: 0.0021 - val_tp: 53.0000 - val_fp: 8.0000 - val_tn: 45492.0000 - val_fn: 16.0000 - val_accuracy: 0.9995 - val_precision: 0.8689 - val_recall: 0.7681 - val_auc: 0.9563 - val_prc: 0.8662 Epoch 23/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0051 - tp: 158.0000 - fp: 31.0000 - tn: 181929.0000 - fn: 158.0000 - accuracy: 0.9990 - precision: 0.8360 - recall: 0.5000 - auc: 0.8833 - prc: 0.6207 - val_loss: 0.0020 - val_tp: 51.0000 - val_fp: 4.0000 - val_tn: 45496.0000 - val_fn: 18.0000 - val_accuracy: 0.9995 - val_precision: 0.9273 - val_recall: 0.7391 - val_auc: 0.9563 - val_prc: 0.8708 Epoch 24/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0049 - tp: 159.0000 - fp: 25.0000 - tn: 181935.0000 - fn: 157.0000 - accuracy: 0.9990 - precision: 0.8641 - recall: 0.5032 - auc: 0.8801 - prc: 0.6329 - val_loss: 0.0020 - val_tp: 52.0000 - val_fp: 4.0000 - val_tn: 45496.0000 - val_fn: 17.0000 - val_accuracy: 0.9995 - val_precision: 0.9286 - val_recall: 0.7536 - val_auc: 0.9563 - val_prc: 0.8745 Epoch 25/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0049 - tp: 157.0000 - fp: 25.0000 - tn: 181935.0000 - fn: 159.0000 - accuracy: 0.9990 - precision: 0.8626 - recall: 0.4968 - auc: 0.8864 - prc: 0.6369 - val_loss: 0.0020 - val_tp: 54.0000 - val_fp: 4.0000 - val_tn: 45496.0000 - val_fn: 15.0000 - val_accuracy: 0.9996 - val_precision: 0.9310 - val_recall: 0.7826 - val_auc: 0.9563 - val_prc: 0.8758 Epoch 26/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0049 - tp: 154.0000 - fp: 21.0000 - tn: 181939.0000 - fn: 162.0000 - accuracy: 0.9990 - precision: 0.8800 - recall: 0.4873 - auc: 0.8706 - prc: 0.6314 - val_loss: 0.0020 - val_tp: 55.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 14.0000 - val_accuracy: 0.9996 - val_precision: 0.9016 - val_recall: 0.7971 - val_auc: 0.9563 - val_prc: 0.8750 Epoch 27/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0051 - tp: 146.0000 - fp: 33.0000 - tn: 181927.0000 - fn: 170.0000 - accuracy: 0.9989 - precision: 0.8156 - recall: 0.4620 - auc: 0.8736 - prc: 0.6080 - val_loss: 0.0019 - val_tp: 55.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 14.0000 - val_accuracy: 0.9996 - val_precision: 0.9167 - val_recall: 0.7971 - val_auc: 0.9563 - val_prc: 0.8780 Epoch 28/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0050 - tp: 161.0000 - fp: 24.0000 - tn: 181936.0000 - fn: 155.0000 - accuracy: 0.9990 - precision: 0.8703 - recall: 0.5095 - auc: 0.8705 - prc: 0.6133 - val_loss: 0.0019 - val_tp: 55.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 14.0000 - val_accuracy: 0.9996 - val_precision: 0.9167 - val_recall: 0.7971 - val_auc: 0.9563 - val_prc: 0.8793 Epoch 29/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0045 - tp: 171.0000 - fp: 24.0000 - tn: 181936.0000 - fn: 145.0000 - accuracy: 0.9991 - precision: 0.8769 - recall: 0.5411 - auc: 0.8912 - prc: 0.6686 - val_loss: 0.0019 - val_tp: 56.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 13.0000 - val_accuracy: 0.9996 - val_precision: 0.9180 - val_recall: 0.8116 - val_auc: 0.9563 - val_prc: 0.8791 Epoch 30/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0043 - tp: 173.0000 - fp: 18.0000 - tn: 181942.0000 - fn: 143.0000 - accuracy: 0.9991 - precision: 0.9058 - recall: 0.5475 - auc: 0.8928 - prc: 0.6809 - val_loss: 0.0019 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9563 - val_prc: 0.8784 Epoch 31/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0047 - tp: 165.0000 - fp: 30.0000 - tn: 181930.0000 - fn: 151.0000 - accuracy: 0.9990 - precision: 0.8462 - recall: 0.5222 - auc: 0.8849 - prc: 0.6529 - val_loss: 0.0019 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9563 - val_prc: 0.8799 Epoch 32/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0048 - tp: 173.0000 - fp: 32.0000 - tn: 181928.0000 - fn: 143.0000 - accuracy: 0.9990 - precision: 0.8439 - recall: 0.5475 - auc: 0.8846 - prc: 0.6361 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9062 - val_recall: 0.8406 - val_auc: 0.9563 - val_prc: 0.8813 Epoch 33/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0046 - tp: 166.0000 - fp: 28.0000 - tn: 181932.0000 - fn: 150.0000 - accuracy: 0.9990 - precision: 0.8557 - recall: 0.5253 - auc: 0.8799 - prc: 0.6417 - val_loss: 0.0019 - val_tp: 59.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 10.0000 - val_accuracy: 0.9996 - val_precision: 0.9077 - val_recall: 0.8551 - val_auc: 0.9563 - val_prc: 0.8787 Epoch 34/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0046 - tp: 170.0000 - fp: 24.0000 - tn: 181936.0000 - fn: 146.0000 - accuracy: 0.9991 - precision: 0.8763 - recall: 0.5380 - auc: 0.8847 - prc: 0.6515 - val_loss: 0.0019 - val_tp: 58.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9062 - val_recall: 0.8406 - val_auc: 0.9563 - val_prc: 0.8822 Epoch 35/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0048 - tp: 166.0000 - fp: 30.0000 - tn: 181930.0000 - fn: 150.0000 - accuracy: 0.9990 - precision: 0.8469 - recall: 0.5253 - auc: 0.8816 - prc: 0.6244 - val_loss: 0.0018 - val_tp: 56.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 13.0000 - val_accuracy: 0.9996 - val_precision: 0.9180 - val_recall: 0.8116 - val_auc: 0.9563 - val_prc: 0.8823 Epoch 36/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0045 - tp: 159.0000 - fp: 27.0000 - tn: 181933.0000 - fn: 157.0000 - accuracy: 0.9990 - precision: 0.8548 - recall: 0.5032 - auc: 0.8976 - prc: 0.6680 - val_loss: 0.0018 - val_tp: 59.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 10.0000 - val_accuracy: 0.9996 - val_precision: 0.9077 - val_recall: 0.8551 - val_auc: 0.9564 - val_prc: 0.8842 Epoch 37/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0043 - tp: 177.0000 - fp: 25.0000 - tn: 181935.0000 - fn: 139.0000 - accuracy: 0.9991 - precision: 0.8762 - recall: 0.5601 - auc: 0.8896 - prc: 0.6850 - val_loss: 0.0018 - val_tp: 59.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 10.0000 - val_accuracy: 0.9996 - val_precision: 0.9077 - val_recall: 0.8551 - val_auc: 0.9563 - val_prc: 0.8839 Epoch 38/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0046 - tp: 168.0000 - fp: 24.0000 - tn: 181936.0000 - fn: 148.0000 - accuracy: 0.9991 - precision: 0.8750 - recall: 0.5316 - auc: 0.8832 - prc: 0.6569 - val_loss: 0.0018 - val_tp: 59.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 10.0000 - val_accuracy: 0.9996 - val_precision: 0.9077 - val_recall: 0.8551 - val_auc: 0.9563 - val_prc: 0.8821 Epoch 39/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0047 - tp: 165.0000 - fp: 29.0000 - tn: 181931.0000 - fn: 151.0000 - accuracy: 0.9990 - precision: 0.8505 - recall: 0.5222 - auc: 0.8833 - prc: 0.6458 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9564 - val_prc: 0.8834 Epoch 40/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0047 - tp: 161.0000 - fp: 27.0000 - tn: 181933.0000 - fn: 155.0000 - accuracy: 0.9990 - precision: 0.8564 - recall: 0.5095 - auc: 0.8801 - prc: 0.6468 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9564 - val_prc: 0.8841 Epoch 41/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0043 - tp: 174.0000 - fp: 30.0000 - tn: 181930.0000 - fn: 142.0000 - accuracy: 0.9991 - precision: 0.8529 - recall: 0.5506 - auc: 0.8881 - prc: 0.6824 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9564 - val_prc: 0.8830 Epoch 42/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0045 - tp: 161.0000 - fp: 27.0000 - tn: 181933.0000 - fn: 155.0000 - accuracy: 0.9990 - precision: 0.8564 - recall: 0.5095 - auc: 0.8707 - prc: 0.6479 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9563 - val_prc: 0.8825 Epoch 43/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0048 - tp: 172.0000 - fp: 24.0000 - tn: 181936.0000 - fn: 144.0000 - accuracy: 0.9991 - precision: 0.8776 - recall: 0.5443 - auc: 0.8753 - prc: 0.6130 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9636 - val_prc: 0.8914 Epoch 44/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0045 - tp: 173.0000 - fp: 30.0000 - tn: 181930.0000 - fn: 143.0000 - accuracy: 0.9991 - precision: 0.8522 - recall: 0.5475 - auc: 0.8833 - prc: 0.6598 - val_loss: 0.0018 - val_tp: 57.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 12.0000 - val_accuracy: 0.9996 - val_precision: 0.9194 - val_recall: 0.8261 - val_auc: 0.9636 - val_prc: 0.8937 Epoch 45/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0043 - tp: 164.0000 - fp: 24.0000 - tn: 181936.0000 - fn: 152.0000 - accuracy: 0.9990 - precision: 0.8723 - recall: 0.5190 - auc: 0.8865 - prc: 0.6724 - val_loss: 0.0018 - val_tp: 57.0000 - val_fp: 4.0000 - val_tn: 45496.0000 - val_fn: 12.0000 - val_accuracy: 0.9996 - val_precision: 0.9344 - val_recall: 0.8261 - val_auc: 0.9636 - val_prc: 0.8939 Epoch 46/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0044 - tp: 165.0000 - fp: 23.0000 - tn: 181937.0000 - fn: 151.0000 - accuracy: 0.9990 - precision: 0.8777 - recall: 0.5222 - auc: 0.8960 - prc: 0.6687 - val_loss: 0.0018 - val_tp: 59.0000 - val_fp: 4.0000 - val_tn: 45496.0000 - val_fn: 10.0000 - val_accuracy: 0.9997 - val_precision: 0.9365 - val_recall: 0.8551 - val_auc: 0.9636 - val_prc: 0.8948 Epoch 47/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0046 - tp: 166.0000 - fp: 25.0000 - tn: 181935.0000 - fn: 150.0000 - accuracy: 0.9990 - precision: 0.8691 - recall: 0.5253 - auc: 0.8801 - prc: 0.6463 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 4.0000 - val_tn: 45496.0000 - val_fn: 11.0000 - val_accuracy: 0.9997 - val_precision: 0.9355 - val_recall: 0.8406 - val_auc: 0.9636 - val_prc: 0.8953 Epoch 48/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0046 - tp: 169.0000 - fp: 21.0000 - tn: 181939.0000 - fn: 147.0000 - accuracy: 0.9991 - precision: 0.8895 - recall: 0.5348 - auc: 0.8738 - prc: 0.6581 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9636 - val_prc: 0.8945 Epoch 49/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0047 - tp: 173.0000 - fp: 30.0000 - tn: 181930.0000 - fn: 143.0000 - accuracy: 0.9991 - precision: 0.8522 - recall: 0.5475 - auc: 0.8786 - prc: 0.6424 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 4.0000 - val_tn: 45496.0000 - val_fn: 11.0000 - val_accuracy: 0.9997 - val_precision: 0.9355 - val_recall: 0.8406 - val_auc: 0.9636 - val_prc: 0.8973 Epoch 50/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0043 - tp: 165.0000 - fp: 22.0000 - tn: 181938.0000 - fn: 151.0000 - accuracy: 0.9991 - precision: 0.8824 - recall: 0.5222 - auc: 0.8914 - prc: 0.6806 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9636 - val_prc: 0.8958 Epoch 51/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0044 - tp: 186.0000 - fp: 35.0000 - tn: 181925.0000 - fn: 130.0000 - accuracy: 0.9991 - precision: 0.8416 - recall: 0.5886 - auc: 0.8864 - prc: 0.6577 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 3.0000 - val_tn: 45497.0000 - val_fn: 11.0000 - val_accuracy: 0.9997 - val_precision: 0.9508 - val_recall: 0.8406 - val_auc: 0.9636 - val_prc: 0.8976 Epoch 52/100 90/90 [==============================] - 0s 6ms/step - loss: 0.0048 - tp: 155.0000 - fp: 27.0000 - tn: 181933.0000 - fn: 161.0000 - accuracy: 0.9990 - precision: 0.8516 - recall: 0.4905 - auc: 0.8769 - prc: 0.6301 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 4.0000 - val_tn: 45496.0000 - val_fn: 11.0000 - val_accuracy: 0.9997 - val_precision: 0.9355 - val_recall: 0.8406 - val_auc: 0.9636 - val_prc: 0.8972 Epoch 53/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0043 - tp: 178.0000 - fp: 26.0000 - tn: 181934.0000 - fn: 138.0000 - accuracy: 0.9991 - precision: 0.8725 - recall: 0.5633 - auc: 0.8818 - prc: 0.6617 - val_loss: 0.0017 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9636 - val_prc: 0.8960 Epoch 54/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0044 - tp: 167.0000 - fp: 21.0000 - tn: 181939.0000 - fn: 149.0000 - accuracy: 0.9991 - precision: 0.8883 - recall: 0.5285 - auc: 0.8897 - prc: 0.6597 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9636 - val_prc: 0.8952 Epoch 55/100 90/90 [==============================] - 1s 6ms/step - loss: 0.0046 - tp: 159.0000 - fp: 26.0000 - tn: 181934.0000 - fn: 157.0000 - accuracy: 0.9990 - precision: 0.8595 - recall: 0.5032 - auc: 0.8754 - prc: 0.6306 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9062 - val_recall: 0.8406 - val_auc: 0.9636 - val_prc: 0.8949 Epoch 56/100 90/90 [==============================] - ETA: 0s - loss: 0.0044 - tp: 182.0000 - fp: 27.0000 - tn: 181933.0000 - fn: 134.0000 - accuracy: 0.9991 - precision: 0.8708 - recall: 0.5759 - auc: 0.8976 - prc: 0.6778Restoring model weights from the end of the best epoch: 46. 90/90 [==============================] - 1s 6ms/step - loss: 0.0044 - tp: 182.0000 - fp: 27.0000 - tn: 181933.0000 - fn: 134.0000 - accuracy: 0.9991 - precision: 0.8708 - recall: 0.5759 - auc: 0.8976 - prc: 0.6778 - val_loss: 0.0018 - val_tp: 58.0000 - val_fp: 5.0000 - val_tn: 45495.0000 - val_fn: 11.0000 - val_accuracy: 0.9996 - val_precision: 0.9206 - val_recall: 0.8406 - val_auc: 0.9636 - val_prc: 0.8943 Epoch 56: early stopping
查看训练历史记录
在本部分,您将针对训练集和验证集生成模型的准确率和损失绘图。这些对于检查过拟合十分有用,您可以在此教程中了解更多信息。
此外,您还可以为您在上面创建的任何指标生成上述绘图。假负例包含在以下示例中。
def plot_metrics(history):
metrics = ['loss', 'prc', 'precision', 'recall']
for n, metric in enumerate(metrics):
name = metric.replace("_"," ").capitalize()
plt.subplot(2,2,n+1)
plt.plot(history.epoch, history.history[metric], color=colors[0], label='Train')
plt.plot(history.epoch, history.history['val_'+metric],
color=colors[0], linestyle="--", label='Val')
plt.xlabel('Epoch')
plt.ylabel(name)
if metric == 'loss':
plt.ylim([0, plt.ylim()[1]])
elif metric == 'auc':
plt.ylim([0.8,1])
else:
plt.ylim([0,1])
plt.legend()
plot_metrics(baseline_history)

注:验证曲线通常比训练曲线表现更好。这主要是由于在评估模型时,随机失活层处于非活动状态。
评估指标
您可以使用混淆矩阵来汇总实际标签与预测标签,其中 X 轴是预测标签,Y 轴是实际标签:
train_predictions_baseline = model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_baseline = model.predict(test_features, batch_size=BATCH_SIZE)
90/90 [==============================] - 0s 1ms/step 28/28 [==============================] - 0s 2ms/step
def plot_cm(labels, predictions, p=0.5):
cm = confusion_matrix(labels, predictions > p)
plt.figure(figsize=(5,5))
sns.heatmap(cm, annot=True, fmt="d")
plt.title('Confusion matrix @{:.2f}'.format(p))
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
print('Legitimate Transactions Detected (True Negatives): ', cm[0][0])
print('Legitimate Transactions Incorrectly Detected (False Positives): ', cm[0][1])
print('Fraudulent Transactions Missed (False Negatives): ', cm[1][0])
print('Fraudulent Transactions Detected (True Positives): ', cm[1][1])
print('Total Fraudulent Transactions: ', np.sum(cm[1]))
在测试数据集上评估您的模型并显示您在上面创建的指标的结果:
baseline_results = model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(model.metrics_names, baseline_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_baseline)
loss : 0.0030497945845127106 tp : 84.0 fp : 12.0 tn : 56843.0 fn : 23.0 accuracy : 0.9993855357170105 precision : 0.875 recall : 0.7850467562675476 auc : 0.9389954805374146 prc : 0.8279591798782349 Legitimate Transactions Detected (True Negatives): 56843 Legitimate Transactions Incorrectly Detected (False Positives): 12 Fraudulent Transactions Missed (False Negatives): 23 Fraudulent Transactions Detected (True Positives): 84 Total Fraudulent Transactions: 107
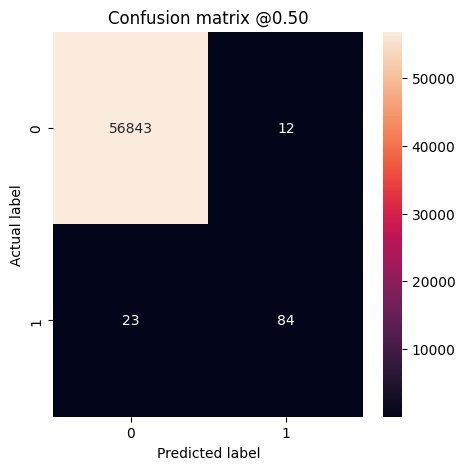
如果模型完美地预测了所有内容,则这是一个对角矩阵,其中偏离主对角线的值(表示不正确的预测)将为零。在这种情况下,矩阵会显示您的假正例相对较少,这意味着被错误标记的合法交易相对较少。但是,您可能希望得到更少的假负例,即使这会增加假正例的数量。这种权衡可能更加可取,因为假负例允许进行欺诈交易,而假正例可能导致向客户发送电子邮件,要求他们验证自己的信用卡活动。
绘制 ROC
现在绘制 ROC。此绘图非常有用,因为它一目了然地显示了模型只需通过调整输出阈值就能达到的性能范围。
def plot_roc(name, labels, predictions, **kwargs):
fp, tp, _ = sklearn.metrics.roc_curve(labels, predictions)
plt.plot(100*fp, 100*tp, label=name, linewidth=2, **kwargs)
plt.xlabel('False positives [%]')
plt.ylabel('True positives [%]')
plt.xlim([-0.5,20])
plt.ylim([80,100.5])
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');

绘制 AUPRC
现在绘制 AUPRC。内插精确率-召回率曲线的下方面积,通过为分类阈值的不同值绘制(召回率、精确率)点获得。根据计算方式,PR AUC 可能相当于模型的平均精确率。
def plot_prc(name, labels, predictions, **kwargs):
precision, recall, _ = sklearn.metrics.precision_recall_curve(labels, predictions)
plt.plot(precision, recall, label=name, linewidth=2, **kwargs)
plt.xlabel('Precision')
plt.ylabel('Recall')
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right');
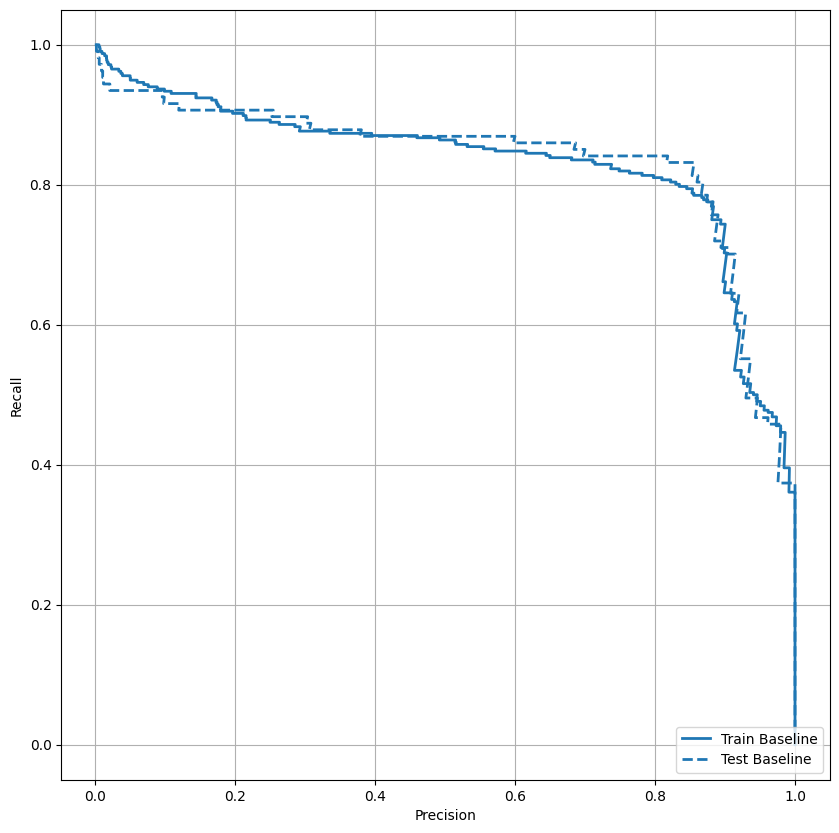
看起来精确率相对较高,但是召回率和 ROC 曲线下方面积 (AUC) 可能并没有您期望的那么高。当试图同时最大限度地提高精确率和召回率时,分类器通常会面临挑战,在处理不平衡数据集时尤其如此。请务必根据您所关心的问题来考虑不同类型错误的代价。在此示例中,假负例(漏掉欺诈交易)可能造成财务损失,而假正例(将交易错误地标记为欺诈)则可能降低用户满意度。
类权重
计算类权重
我们的目标是识别欺诈交易,但您没有很多可以使用的此类正样本,因此您希望分类器提高可用的少数样本的权重。为此,您可以使用参数将 Keras 权重传递给每个类。这些权重将使模型“更加关注”来自代表不足的类的样本。
# Scaling by total/2 helps keep the loss to a similar magnitude.
# The sum of the weights of all examples stays the same.
weight_for_0 = (1 / neg) * (total / 2.0)
weight_for_1 = (1 / pos) * (total / 2.0)
class_weight = {0: weight_for_0, 1: weight_for_1}
print('Weight for class 0: {:.2f}'.format(weight_for_0))
print('Weight for class 1: {:.2f}'.format(weight_for_1))
Weight for class 0: 0.50 Weight for class 1: 289.44
使用类权重训练模型
现在,尝试使用类权重对模型进行重新训练和评估,以了解其对预测的影响。
注:使用 class_weights 会改变损失范围。这可能会影响训练的稳定性,具体取决于优化器。步长取决于梯度大小的优化器(如 optimizers.SGD)可能会失效。此处使用的优化器(optimizers.Adam)不受缩放更改的影响。还要注意,由于加权,两个模型之间的总损失不具可比性。
weighted_model = make_model()
weighted_model.load_weights(initial_weights)
weighted_history = weighted_model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks = [early_stopping],
validation_data=(val_features, val_labels),
# The class weights go here
class_weight=class_weight)
Epoch 1/100 90/90 [==============================] - 3s 12ms/step - loss: 3.4540 - tp: 127.0000 - fp: 28.0000 - tn: 238787.0000 - fn: 296.0000 - accuracy: 0.9986 - precision: 0.8194 - recall: 0.3002 - auc: 0.7327 - prc: 0.3224 - val_loss: 0.0070 - val_tp: 9.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 60.0000 - val_accuracy: 0.9986 - val_precision: 0.6000 - val_recall: 0.1304 - val_auc: 0.8538 - val_prc: 0.4746 Epoch 2/100 90/90 [==============================] - 1s 6ms/step - loss: 1.8967 - tp: 106.0000 - fp: 48.0000 - tn: 181912.0000 - fn: 210.0000 - accuracy: 0.9986 - precision: 0.6883 - recall: 0.3354 - auc: 0.7954 - prc: 0.3507 - val_loss: 0.0049 - val_tp: 48.0000 - val_fp: 6.0000 - val_tn: 45494.0000 - val_fn: 21.0000 - val_accuracy: 0.9994 - val_precision: 0.8889 - val_recall: 0.6957 - val_auc: 0.9396 - val_prc: 0.6825 Epoch 3/100 90/90 [==============================] - 1s 6ms/step - loss: 1.2148 - tp: 165.0000 - fp: 131.0000 - tn: 181829.0000 - fn: 151.0000 - accuracy: 0.9985 - precision: 0.5574 - recall: 0.5222 - auc: 0.8611 - prc: 0.4673 - val_loss: 0.0056 - val_tp: 53.0000 - val_fp: 11.0000 - val_tn: 45489.0000 - val_fn: 16.0000 - val_accuracy: 0.9994 - val_precision: 0.8281 - val_recall: 0.7681 - val_auc: 0.9592 - val_prc: 0.7340 Epoch 4/100 90/90 [==============================] - 1s 6ms/step - loss: 0.9954 - tp: 184.0000 - fp: 354.0000 - tn: 181606.0000 - fn: 132.0000 - accuracy: 0.9973 - precision: 0.3420 - recall: 0.5823 - auc: 0.8707 - prc: 0.4738 - val_loss: 0.0071 - val_tp: 58.0000 - val_fp: 15.0000 - val_tn: 45485.0000 - val_fn: 11.0000 - val_accuracy: 0.9994 - val_precision: 0.7945 - val_recall: 0.8406 - val_auc: 0.9857 - val_prc: 0.7529 Epoch 5/100 90/90 [==============================] - 1s 6ms/step - loss: 0.8191 - tp: 212.0000 - fp: 650.0000 - tn: 181310.0000 - fn: 104.0000 - accuracy: 0.9959 - precision: 0.2459 - recall: 0.6709 - auc: 0.8850 - prc: 0.4946 - val_loss: 0.0097 - val_tp: 59.0000 - val_fp: 29.0000 - val_tn: 45471.0000 - val_fn: 10.0000 - val_accuracy: 0.9991 - val_precision: 0.6705 - val_recall: 0.8551 - val_auc: 0.9918 - val_prc: 0.7607 Epoch 6/100 90/90 [==============================] - 1s 6ms/step - loss: 0.6886 - tp: 225.0000 - fp: 1145.0000 - tn: 180815.0000 - fn: 91.0000 - accuracy: 0.9932 - precision: 0.1642 - recall: 0.7120 - auc: 0.8986 - prc: 0.4293 - val_loss: 0.0142 - val_tp: 59.0000 - val_fp: 89.0000 - val_tn: 45411.0000 - val_fn: 10.0000 - val_accuracy: 0.9978 - val_precision: 0.3986 - val_recall: 0.8551 - val_auc: 0.9930 - val_prc: 0.7548 Epoch 7/100 90/90 [==============================] - 1s 6ms/step - loss: 0.6061 - tp: 240.0000 - fp: 1686.0000 - tn: 180274.0000 - fn: 76.0000 - accuracy: 0.9903 - precision: 0.1246 - recall: 0.7595 - auc: 0.9086 - prc: 0.3771 - val_loss: 0.0198 - val_tp: 60.0000 - val_fp: 182.0000 - val_tn: 45318.0000 - val_fn: 9.0000 - val_accuracy: 0.9958 - val_precision: 0.2479 - val_recall: 0.8696 - val_auc: 0.9946 - val_prc: 0.7211 Epoch 8/100 90/90 [==============================] - 1s 6ms/step - loss: 0.6127 - tp: 233.0000 - fp: 2287.0000 - tn: 179673.0000 - fn: 83.0000 - accuracy: 0.9870 - precision: 0.0925 - recall: 0.7373 - auc: 0.9071 - prc: 0.3235 - val_loss: 0.0276 - val_tp: 64.0000 - val_fp: 340.0000 - val_tn: 45160.0000 - val_fn: 5.0000 - val_accuracy: 0.9924 - val_precision: 0.1584 - val_recall: 0.9275 - val_auc: 0.9953 - val_prc: 0.6965 Epoch 9/100 90/90 [==============================] - 1s 6ms/step - loss: 0.4657 - tp: 244.0000 - fp: 3136.0000 - tn: 178824.0000 - fn: 72.0000 - accuracy: 0.9824 - precision: 0.0722 - recall: 0.7722 - auc: 0.9334 - prc: 0.2770 - val_loss: 0.0385 - val_tp: 64.0000 - val_fp: 514.0000 - val_tn: 44986.0000 - val_fn: 5.0000 - val_accuracy: 0.9886 - val_precision: 0.1107 - val_recall: 0.9275 - val_auc: 0.9953 - val_prc: 0.6873 Epoch 10/100 90/90 [==============================] - 1s 6ms/step - loss: 0.4505 - tp: 254.0000 - fp: 4030.0000 - tn: 177930.0000 - fn: 62.0000 - accuracy: 0.9776 - precision: 0.0593 - recall: 0.8038 - auc: 0.9320 - prc: 0.2187 - val_loss: 0.0484 - val_tp: 64.0000 - val_fp: 642.0000 - val_tn: 44858.0000 - val_fn: 5.0000 - val_accuracy: 0.9858 - val_precision: 0.0907 - val_recall: 0.9275 - val_auc: 0.9953 - val_prc: 0.6514 Epoch 11/100 90/90 [==============================] - 1s 6ms/step - loss: 0.4498 - tp: 252.0000 - fp: 4605.0000 - tn: 177355.0000 - fn: 64.0000 - accuracy: 0.9744 - precision: 0.0519 - recall: 0.7975 - auc: 0.9242 - prc: 0.2122 - val_loss: 0.0548 - val_tp: 64.0000 - val_fp: 694.0000 - val_tn: 44806.0000 - val_fn: 5.0000 - val_accuracy: 0.9847 - val_precision: 0.0844 - val_recall: 0.9275 - val_auc: 0.9953 - val_prc: 0.6065 Epoch 12/100 90/90 [==============================] - 1s 6ms/step - loss: 0.4053 - tp: 260.0000 - fp: 5182.0000 - tn: 176778.0000 - fn: 56.0000 - accuracy: 0.9713 - precision: 0.0478 - recall: 0.8228 - auc: 0.9284 - prc: 0.1952 - val_loss: 0.0608 - val_tp: 64.0000 - val_fp: 767.0000 - val_tn: 44733.0000 - val_fn: 5.0000 - val_accuracy: 0.9831 - val_precision: 0.0770 - val_recall: 0.9275 - val_auc: 0.9953 - val_prc: 0.6025 Epoch 13/100 90/90 [==============================] - 1s 6ms/step - loss: 0.3426 - tp: 263.0000 - fp: 5964.0000 - tn: 175996.0000 - fn: 53.0000 - accuracy: 0.9670 - precision: 0.0422 - recall: 0.8323 - auc: 0.9503 - prc: 0.1911 - val_loss: 0.0683 - val_tp: 64.0000 - val_fp: 849.0000 - val_tn: 44651.0000 - val_fn: 5.0000 - val_accuracy: 0.9813 - val_precision: 0.0701 - val_recall: 0.9275 - val_auc: 0.9950 - val_prc: 0.5961 Epoch 14/100 90/90 [==============================] - 1s 6ms/step - loss: 0.3627 - tp: 268.0000 - fp: 6356.0000 - tn: 175604.0000 - fn: 48.0000 - accuracy: 0.9649 - precision: 0.0405 - recall: 0.8481 - auc: 0.9365 - prc: 0.1903 - val_loss: 0.0714 - val_tp: 64.0000 - val_fp: 880.0000 - val_tn: 44620.0000 - val_fn: 5.0000 - val_accuracy: 0.9806 - val_precision: 0.0678 - val_recall: 0.9275 - val_auc: 0.9951 - val_prc: 0.5914 Epoch 15/100 90/90 [==============================] - 1s 6ms/step - loss: 0.3306 - tp: 271.0000 - fp: 6756.0000 - tn: 175204.0000 - fn: 45.0000 - accuracy: 0.9627 - precision: 0.0386 - recall: 0.8576 - auc: 0.9458 - prc: 0.2015 - val_loss: 0.0741 - val_tp: 64.0000 - val_fp: 914.0000 - val_tn: 44586.0000 - val_fn: 5.0000 - val_accuracy: 0.9798 - val_precision: 0.0654 - val_recall: 0.9275 - val_auc: 0.9948 - val_prc: 0.5921 Epoch 16/100 90/90 [==============================] - 1s 6ms/step - loss: 0.3222 - tp: 272.0000 - fp: 6837.0000 - tn: 175123.0000 - fn: 44.0000 - accuracy: 0.9622 - precision: 0.0383 - recall: 0.8608 - auc: 0.9446 - prc: 0.1837 - val_loss: 0.0752 - val_tp: 65.0000 - val_fp: 923.0000 - val_tn: 44577.0000 - val_fn: 4.0000 - val_accuracy: 0.9797 - val_precision: 0.0658 - val_recall: 0.9420 - val_auc: 0.9947 - val_prc: 0.5894 Epoch 17/100 90/90 [==============================] - 1s 6ms/step - loss: 0.3474 - tp: 267.0000 - fp: 7262.0000 - tn: 174698.0000 - fn: 49.0000 - accuracy: 0.9599 - precision: 0.0355 - recall: 0.8449 - auc: 0.9397 - prc: 0.1785 - val_loss: 0.0808 - val_tp: 65.0000 - val_fp: 979.0000 - val_tn: 44521.0000 - val_fn: 4.0000 - val_accuracy: 0.9784 - val_precision: 0.0623 - val_recall: 0.9420 - val_auc: 0.9947 - val_prc: 0.5926 Epoch 18/100 90/90 [==============================] - 1s 6ms/step - loss: 0.3525 - tp: 267.0000 - fp: 7350.0000 - tn: 174610.0000 - fn: 49.0000 - accuracy: 0.9594 - precision: 0.0351 - recall: 0.8449 - auc: 0.9373 - prc: 0.1762 - val_loss: 0.0806 - val_tp: 65.0000 - val_fp: 977.0000 - val_tn: 44523.0000 - val_fn: 4.0000 - val_accuracy: 0.9785 - val_precision: 0.0624 - val_recall: 0.9420 - val_auc: 0.9947 - val_prc: 0.5927 Epoch 19/100 90/90 [==============================] - 1s 6ms/step - loss: 0.3757 - tp: 269.0000 - fp: 7315.0000 - tn: 174645.0000 - fn: 47.0000 - accuracy: 0.9596 - precision: 0.0355 - recall: 0.8513 - auc: 0.9277 - prc: 0.1830 - val_loss: 0.0779 - val_tp: 65.0000 - val_fp: 949.0000 - val_tn: 44551.0000 - val_fn: 4.0000 - val_accuracy: 0.9791 - val_precision: 0.0641 - val_recall: 0.9420 - val_auc: 0.9948 - val_prc: 0.5936 Epoch 20/100 90/90 [==============================] - 1s 6ms/step - loss: 0.3146 - tp: 271.0000 - fp: 7173.0000 - tn: 174787.0000 - fn: 45.0000 - accuracy: 0.9604 - precision: 0.0364 - recall: 0.8576 - auc: 0.9483 - prc: 0.1861 - val_loss: 0.0790 - val_tp: 65.0000 - val_fp: 944.0000 - val_tn: 44556.0000 - val_fn: 4.0000 - val_accuracy: 0.9792 - val_precision: 0.0644 - val_recall: 0.9420 - val_auc: 0.9948 - val_prc: 0.5963 Epoch 21/100 87/90 [============================>.] - ETA: 0s - loss: 0.3226 - tp: 268.0000 - fp: 7036.0000 - tn: 170831.0000 - fn: 41.0000 - accuracy: 0.9603 - precision: 0.0367 - recall: 0.8673 - auc: 0.9444 - prc: 0.1947Restoring model weights from the end of the best epoch: 11. 90/90 [==============================] - 1s 6ms/step - loss: 0.3172 - tp: 275.0000 - fp: 7203.0000 - tn: 174757.0000 - fn: 41.0000 - accuracy: 0.9603 - precision: 0.0368 - recall: 0.8703 - auc: 0.9455 - prc: 0.1949 - val_loss: 0.0773 - val_tp: 65.0000 - val_fp: 908.0000 - val_tn: 44592.0000 - val_fn: 4.0000 - val_accuracy: 0.9800 - val_precision: 0.0668 - val_recall: 0.9420 - val_auc: 0.9950 - val_prc: 0.6021 Epoch 21: early stopping
查看训练历史记录
plot_metrics(weighted_history)

评估指标
train_predictions_weighted = weighted_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_weighted = weighted_model.predict(test_features, batch_size=BATCH_SIZE)
90/90 [==============================] - 0s 1ms/step 28/28 [==============================] - 0s 2ms/step
weighted_results = weighted_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(weighted_model.metrics_names, weighted_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_weighted)
loss : 0.054440323263406754 tp : 94.0 fp : 832.0 tn : 56023.0 fn : 13.0 accuracy : 0.985165536403656 precision : 0.1015118807554245 recall : 0.8785046935081482 auc : 0.9787468910217285 prc : 0.6335744857788086 Legitimate Transactions Detected (True Negatives): 56023 Legitimate Transactions Incorrectly Detected (False Positives): 832 Fraudulent Transactions Missed (False Negatives): 13 Fraudulent Transactions Detected (True Positives): 94 Total Fraudulent Transactions: 107

在这里,您可以看到,使用类权重时,由于存在更多假正例,准确率和精确率较低,但是相反,由于模型也找到了更多真正例,召回率和 AUC 较高。尽管准确率较低,但是此模型具有较高的召回率(且识别出了更多欺诈交易)。当然,两种类型的错误都有代价(您也不希望因将过多合法交易标记为欺诈来打扰客户)。请在应用时认真权衡这些不同类型的错误。
绘制 ROC
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');

绘制 AUPRC
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right');

过采样
对占少数的类进行过采样
一种相关方法是通过对占少数的类进行过采样来对数据集进行重新采样。
pos_features = train_features[bool_train_labels]
neg_features = train_features[~bool_train_labels]
pos_labels = train_labels[bool_train_labels]
neg_labels = train_labels[~bool_train_labels]
使用 NumPy
您可以通过从正样本中选择正确数量的随机索引来手动平衡数据集:
ids = np.arange(len(pos_features))
choices = np.random.choice(ids, len(neg_features))
res_pos_features = pos_features[choices]
res_pos_labels = pos_labels[choices]
res_pos_features.shape
(181960, 29)
resampled_features = np.concatenate([res_pos_features, neg_features], axis=0)
resampled_labels = np.concatenate([res_pos_labels, neg_labels], axis=0)
order = np.arange(len(resampled_labels))
np.random.shuffle(order)
resampled_features = resampled_features[order]
resampled_labels = resampled_labels[order]
resampled_features.shape
(363920, 29)
使用 tf.data
如果您使用的是 tf.data,则生成平衡样本最简单的方法是从 positive 和 negative 数据集开始,然后将它们合并。有关更多示例,请参阅 tf.data 指南。
BUFFER_SIZE = 100000
def make_ds(features, labels):
ds = tf.data.Dataset.from_tensor_slices((features, labels))#.cache()
ds = ds.shuffle(BUFFER_SIZE).repeat()
return ds
pos_ds = make_ds(pos_features, pos_labels)
neg_ds = make_ds(neg_features, neg_labels)
每个数据集都会提供 (feature, label) 对:
for features, label in pos_ds.take(1):
print("Features:\n", features.numpy())
print()
print("Label: ", label.numpy())
Features: [ 0.9559428 0.80097054 -1.53757364 2.98558412 0.98626604 -0.64296745 0.58623809 -0.1389485 -1.36773827 0.23749502 1.42062045 -0.28331678 -0.7594046 -2.88674106 -1.86392462 1.81905823 2.28344955 1.42037765 -1.88417858 -0.29778025 -0.2085476 -0.49742697 0.06843843 -0.3974017 0.32761487 -0.00762779 -0.06715681 0.01644712 -0.48884179] Label: 1
使用 experimental.sample_from_datasets 将二者合并起来:
resampled_ds = tf.data.Dataset.sample_from_datasets([pos_ds, neg_ds], weights=[0.5, 0.5])
resampled_ds = resampled_ds.batch(BATCH_SIZE).prefetch(2)
for features, label in resampled_ds.take(1):
print(label.numpy().mean())
0.49072265625
要使用此数据集,您需要每个周期的步骤数。
在这种情况下,“周期”的定义就不那么明确了。假设它是遍历一次所有负样本所需的批次数量:
resampled_steps_per_epoch = np.ceil(2.0*neg/BATCH_SIZE)
resampled_steps_per_epoch
278.0
在过采样数据上进行训练
现在尝试使用重新采样后的数据集(而非使用类权重)来训练模型,对比一下这两种方法有何区别。
注:因为数据平衡是通过复制正样本实现的,所以数据集的总大小变大了,且每个周期运行的训练步骤也增加了。
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
val_ds = tf.data.Dataset.from_tensor_slices((val_features, val_labels)).cache()
val_ds = val_ds.batch(BATCH_SIZE).prefetch(2)
resampled_history = resampled_model.fit(
resampled_ds,
epochs=EPOCHS,
steps_per_epoch=resampled_steps_per_epoch,
callbacks = [early_stopping],
validation_data=val_ds)
Epoch 1/100 278/278 [==============================] - 9s 26ms/step - loss: 0.6244 - tp: 196970.0000 - fp: 41577.0000 - tn: 299585.0000 - fn: 88174.0000 - accuracy: 0.7928 - precision: 0.8257 - recall: 0.6908 - auc: 0.8304 - prc: 0.8662 - val_loss: 0.1924 - val_tp: 63.0000 - val_fp: 819.0000 - val_tn: 44681.0000 - val_fn: 6.0000 - val_accuracy: 0.9819 - val_precision: 0.0714 - val_recall: 0.9130 - val_auc: 0.9944 - val_prc: 0.7565 Epoch 2/100 278/278 [==============================] - 7s 24ms/step - loss: 0.2485 - tp: 223798.0000 - fp: 14518.0000 - tn: 270446.0000 - fn: 60582.0000 - accuracy: 0.8681 - precision: 0.9391 - recall: 0.7870 - auc: 0.9596 - prc: 0.9661 - val_loss: 0.1043 - val_tp: 66.0000 - val_fp: 746.0000 - val_tn: 44754.0000 - val_fn: 3.0000 - val_accuracy: 0.9836 - val_precision: 0.0813 - val_recall: 0.9565 - val_auc: 0.9961 - val_prc: 0.7801 Epoch 3/100 278/278 [==============================] - 7s 23ms/step - loss: 0.1958 - tp: 251598.0000 - fp: 13396.0000 - tn: 271898.0000 - fn: 32452.0000 - accuracy: 0.9195 - precision: 0.9494 - recall: 0.8858 - auc: 0.9782 - prc: 0.9796 - val_loss: 0.0813 - val_tp: 66.0000 - val_fp: 799.0000 - val_tn: 44701.0000 - val_fn: 3.0000 - val_accuracy: 0.9824 - val_precision: 0.0763 - val_recall: 0.9565 - val_auc: 0.9957 - val_prc: 0.7847 Epoch 4/100 278/278 [==============================] - 6s 23ms/step - loss: 0.1683 - tp: 263076.0000 - fp: 13950.0000 - tn: 270190.0000 - fn: 22128.0000 - accuracy: 0.9366 - precision: 0.9496 - recall: 0.9224 - auc: 0.9847 - prc: 0.9851 - val_loss: 0.0677 - val_tp: 66.0000 - val_fp: 760.0000 - val_tn: 44740.0000 - val_fn: 3.0000 - val_accuracy: 0.9833 - val_precision: 0.0799 - val_recall: 0.9565 - val_auc: 0.9954 - val_prc: 0.7691 Epoch 5/100 278/278 [==============================] - 6s 23ms/step - loss: 0.1513 - tp: 267889.0000 - fp: 14968.0000 - tn: 269576.0000 - fn: 16911.0000 - accuracy: 0.9440 - precision: 0.9471 - recall: 0.9406 - auc: 0.9878 - prc: 0.9878 - val_loss: 0.0582 - val_tp: 66.0000 - val_fp: 747.0000 - val_tn: 44753.0000 - val_fn: 3.0000 - val_accuracy: 0.9835 - val_precision: 0.0812 - val_recall: 0.9565 - val_auc: 0.9957 - val_prc: 0.7716 Epoch 6/100 278/278 [==============================] - 6s 23ms/step - loss: 0.1383 - tp: 272263.0000 - fp: 15458.0000 - tn: 269001.0000 - fn: 12622.0000 - accuracy: 0.9507 - precision: 0.9463 - recall: 0.9557 - auc: 0.9897 - prc: 0.9895 - val_loss: 0.0514 - val_tp: 66.0000 - val_fp: 716.0000 - val_tn: 44784.0000 - val_fn: 3.0000 - val_accuracy: 0.9842 - val_precision: 0.0844 - val_recall: 0.9565 - val_auc: 0.9961 - val_prc: 0.7749 Epoch 7/100 278/278 [==============================] - 6s 23ms/step - loss: 0.1279 - tp: 275144.0000 - fp: 15791.0000 - tn: 268338.0000 - fn: 10071.0000 - accuracy: 0.9546 - precision: 0.9457 - recall: 0.9647 - auc: 0.9912 - prc: 0.9909 - val_loss: 0.0474 - val_tp: 65.0000 - val_fp: 720.0000 - val_tn: 44780.0000 - val_fn: 4.0000 - val_accuracy: 0.9841 - val_precision: 0.0828 - val_recall: 0.9420 - val_auc: 0.9955 - val_prc: 0.7776 Epoch 8/100 278/278 [==============================] - 6s 23ms/step - loss: 0.1200 - tp: 276934.0000 - fp: 16125.0000 - tn: 267921.0000 - fn: 8364.0000 - accuracy: 0.9570 - precision: 0.9450 - recall: 0.9707 - auc: 0.9921 - prc: 0.9918 - val_loss: 0.0443 - val_tp: 65.0000 - val_fp: 716.0000 - val_tn: 44784.0000 - val_fn: 4.0000 - val_accuracy: 0.9842 - val_precision: 0.0832 - val_recall: 0.9420 - val_auc: 0.9948 - val_prc: 0.7683 Epoch 9/100 278/278 [==============================] - 7s 24ms/step - loss: 0.1126 - tp: 278043.0000 - fp: 16472.0000 - tn: 267971.0000 - fn: 6858.0000 - accuracy: 0.9590 - precision: 0.9441 - recall: 0.9759 - auc: 0.9928 - prc: 0.9925 - val_loss: 0.0407 - val_tp: 65.0000 - val_fp: 664.0000 - val_tn: 44836.0000 - val_fn: 4.0000 - val_accuracy: 0.9853 - val_precision: 0.0892 - val_recall: 0.9420 - val_auc: 0.9941 - val_prc: 0.7696 Epoch 10/100 278/278 [==============================] - 7s 24ms/step - loss: 0.1061 - tp: 278163.0000 - fp: 16128.0000 - tn: 269479.0000 - fn: 5574.0000 - accuracy: 0.9619 - precision: 0.9452 - recall: 0.9804 - auc: 0.9936 - prc: 0.9931 - val_loss: 0.0370 - val_tp: 65.0000 - val_fp: 620.0000 - val_tn: 44880.0000 - val_fn: 4.0000 - val_accuracy: 0.9863 - val_precision: 0.0949 - val_recall: 0.9420 - val_auc: 0.9935 - val_prc: 0.7715 Epoch 11/100 278/278 [==============================] - 6s 23ms/step - loss: 0.0997 - tp: 278905.0000 - fp: 15891.0000 - tn: 269709.0000 - fn: 4839.0000 - accuracy: 0.9636 - precision: 0.9461 - recall: 0.9829 - auc: 0.9942 - prc: 0.9937 - val_loss: 0.0342 - val_tp: 65.0000 - val_fp: 585.0000 - val_tn: 44915.0000 - val_fn: 4.0000 - val_accuracy: 0.9871 - val_precision: 0.1000 - val_recall: 0.9420 - val_auc: 0.9931 - val_prc: 0.7760 Epoch 12/100 276/278 [============================>.] - ETA: 0s - loss: 0.0944 - tp: 278484.0000 - fp: 15374.0000 - tn: 267452.0000 - fn: 3938.0000 - accuracy: 0.9658 - precision: 0.9477 - recall: 0.9861 - auc: 0.9946 - prc: 0.9942Restoring model weights from the end of the best epoch: 2. 278/278 [==============================] - 6s 23ms/step - loss: 0.0944 - tp: 280510.0000 - fp: 15490.0000 - tn: 269381.0000 - fn: 3963.0000 - accuracy: 0.9658 - precision: 0.9477 - recall: 0.9861 - auc: 0.9946 - prc: 0.9942 - val_loss: 0.0319 - val_tp: 65.0000 - val_fp: 576.0000 - val_tn: 44924.0000 - val_fn: 4.0000 - val_accuracy: 0.9873 - val_precision: 0.1014 - val_recall: 0.9420 - val_auc: 0.9869 - val_prc: 0.7762 Epoch 12: early stopping
如果训练过程在每次梯度更新时都考虑整个数据集,那么这种过采样将与类加权基本相同。
但是,当按批次训练模型时(如您在上面所做的那样),过采样的数据将提供更加平滑的梯度信号:不在一个权重较大的批次中显示每个正样本,而是在许多具有较小权重的不同批次中分别显示。
这种更平滑的梯度信号使训练模型变得更加容易。
查看训练历史记录
请注意,此处的指标分布将有所不同,因为训练数据与验证和测试数据的分布完全不同。
plot_metrics(resampled_history )

重新训练
由于在平衡数据上训练更加容易,上面的训练过程可能很快就会过拟合。
因此,请打破周期,使 callbacks.EarlyStopping 能够更好地控制停止训练的时间。
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
resampled_history = resampled_model.fit(
resampled_ds,
# These are not real epochs
steps_per_epoch = 20,
epochs=10*EPOCHS,
callbacks = [early_stopping],
validation_data=(val_ds))
Epoch 1/1000 20/20 [==============================] - 3s 55ms/step - loss: 1.8818 - tp: 7147.0000 - fp: 3701.0000 - tn: 62207.0000 - fn: 13474.0000 - accuracy: 0.8015 - precision: 0.6588 - recall: 0.3466 - auc: 0.7204 - prc: 0.5663 - val_loss: 0.3562 - val_tp: 18.0000 - val_fp: 3378.0000 - val_tn: 42122.0000 - val_fn: 51.0000 - val_accuracy: 0.9248 - val_precision: 0.0053 - val_recall: 0.2609 - val_auc: 0.5310 - val_prc: 0.0789 Epoch 2/1000 20/20 [==============================] - 1s 30ms/step - loss: 1.2506 - tp: 9432.0000 - fp: 3742.0000 - tn: 16690.0000 - fn: 11096.0000 - accuracy: 0.6377 - precision: 0.7160 - recall: 0.4595 - auc: 0.5656 - prc: 0.7088 - val_loss: 0.3813 - val_tp: 46.0000 - val_fp: 4274.0000 - val_tn: 41226.0000 - val_fn: 23.0000 - val_accuracy: 0.9057 - val_precision: 0.0106 - val_recall: 0.6667 - val_auc: 0.7818 - val_prc: 0.3564 Epoch 3/1000 20/20 [==============================] - 1s 30ms/step - loss: 0.9031 - tp: 11130.0000 - fp: 4216.0000 - tn: 16301.0000 - fn: 9313.0000 - accuracy: 0.6697 - precision: 0.7253 - recall: 0.5444 - auc: 0.6484 - prc: 0.7620 - val_loss: 0.3923 - val_tp: 57.0000 - val_fp: 4628.0000 - val_tn: 40872.0000 - val_fn: 12.0000 - val_accuracy: 0.8982 - val_precision: 0.0122 - val_recall: 0.8261 - val_auc: 0.9040 - val_prc: 0.5297 Epoch 4/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.6819 - tp: 12966.0000 - fp: 4063.0000 - tn: 16442.0000 - fn: 7489.0000 - accuracy: 0.7180 - precision: 0.7614 - recall: 0.6339 - auc: 0.7355 - prc: 0.8188 - val_loss: 0.3901 - val_tp: 60.0000 - val_fp: 4341.0000 - val_tn: 41159.0000 - val_fn: 9.0000 - val_accuracy: 0.9045 - val_precision: 0.0136 - val_recall: 0.8696 - val_auc: 0.9306 - val_prc: 0.6600 Epoch 5/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.5618 - tp: 14319.0000 - fp: 4049.0000 - tn: 16518.0000 - fn: 6074.0000 - accuracy: 0.7529 - precision: 0.7796 - recall: 0.7022 - auc: 0.7971 - prc: 0.8594 - val_loss: 0.3759 - val_tp: 62.0000 - val_fp: 3600.0000 - val_tn: 41900.0000 - val_fn: 7.0000 - val_accuracy: 0.9208 - val_precision: 0.0169 - val_recall: 0.8986 - val_auc: 0.9432 - val_prc: 0.6929 Epoch 6/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.4880 - tp: 15347.0000 - fp: 3721.0000 - tn: 16696.0000 - fn: 5196.0000 - accuracy: 0.7823 - precision: 0.8049 - recall: 0.7471 - auc: 0.8385 - prc: 0.8877 - val_loss: 0.3542 - val_tp: 63.0000 - val_fp: 2857.0000 - val_tn: 42643.0000 - val_fn: 6.0000 - val_accuracy: 0.9372 - val_precision: 0.0216 - val_recall: 0.9130 - val_auc: 0.9539 - val_prc: 0.7195 Epoch 7/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.4461 - tp: 15816.0000 - fp: 3280.0000 - tn: 17103.0000 - fn: 4761.0000 - accuracy: 0.8037 - precision: 0.8282 - recall: 0.7686 - auc: 0.8619 - prc: 0.9038 - val_loss: 0.3301 - val_tp: 64.0000 - val_fp: 2195.0000 - val_tn: 43305.0000 - val_fn: 5.0000 - val_accuracy: 0.9517 - val_precision: 0.0283 - val_recall: 0.9275 - val_auc: 0.9639 - val_prc: 0.7314 Epoch 8/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.4191 - tp: 15893.0000 - fp: 2891.0000 - tn: 17619.0000 - fn: 4557.0000 - accuracy: 0.8182 - precision: 0.8461 - recall: 0.7772 - auc: 0.8764 - prc: 0.9124 - val_loss: 0.3054 - val_tp: 64.0000 - val_fp: 1742.0000 - val_tn: 43758.0000 - val_fn: 5.0000 - val_accuracy: 0.9617 - val_precision: 0.0354 - val_recall: 0.9275 - val_auc: 0.9734 - val_prc: 0.7366 Epoch 9/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.3895 - tp: 16135.0000 - fp: 2567.0000 - tn: 17914.0000 - fn: 4344.0000 - accuracy: 0.8313 - precision: 0.8627 - recall: 0.7879 - auc: 0.8927 - prc: 0.9221 - val_loss: 0.2812 - val_tp: 63.0000 - val_fp: 1410.0000 - val_tn: 44090.0000 - val_fn: 6.0000 - val_accuracy: 0.9689 - val_precision: 0.0428 - val_recall: 0.9130 - val_auc: 0.9811 - val_prc: 0.7399 Epoch 10/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.3720 - tp: 16397.0000 - fp: 2348.0000 - tn: 18019.0000 - fn: 4196.0000 - accuracy: 0.8402 - precision: 0.8747 - recall: 0.7962 - auc: 0.9013 - prc: 0.9290 - val_loss: 0.2592 - val_tp: 62.0000 - val_fp: 1199.0000 - val_tn: 44301.0000 - val_fn: 7.0000 - val_accuracy: 0.9735 - val_precision: 0.0492 - val_recall: 0.8986 - val_auc: 0.9869 - val_prc: 0.7455 Epoch 11/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.3445 - tp: 16567.0000 - fp: 1952.0000 - tn: 18519.0000 - fn: 3922.0000 - accuracy: 0.8566 - precision: 0.8946 - recall: 0.8086 - auc: 0.9149 - prc: 0.9377 - val_loss: 0.2394 - val_tp: 62.0000 - val_fp: 1050.0000 - val_tn: 44450.0000 - val_fn: 7.0000 - val_accuracy: 0.9768 - val_precision: 0.0558 - val_recall: 0.8986 - val_auc: 0.9902 - val_prc: 0.7474 Epoch 12/1000 20/20 [==============================] - 1s 28ms/step - loss: 0.3299 - tp: 16021.0000 - fp: 1682.0000 - tn: 18721.0000 - fn: 4536.0000 - accuracy: 0.8482 - precision: 0.9050 - recall: 0.7793 - auc: 0.9221 - prc: 0.9422 - val_loss: 0.2220 - val_tp: 62.0000 - val_fp: 946.0000 - val_tn: 44554.0000 - val_fn: 7.0000 - val_accuracy: 0.9791 - val_precision: 0.0615 - val_recall: 0.8986 - val_auc: 0.9922 - val_prc: 0.7511 Epoch 13/1000 20/20 [==============================] - 1s 32ms/step - loss: 0.3143 - tp: 15899.0000 - fp: 1497.0000 - tn: 19005.0000 - fn: 4559.0000 - accuracy: 0.8521 - precision: 0.9139 - recall: 0.7772 - auc: 0.9297 - prc: 0.9467 - val_loss: 0.2055 - val_tp: 62.0000 - val_fp: 882.0000 - val_tn: 44618.0000 - val_fn: 7.0000 - val_accuracy: 0.9805 - val_precision: 0.0657 - val_recall: 0.8986 - val_auc: 0.9934 - val_prc: 0.7536 Epoch 14/1000 20/20 [==============================] - 1s 30ms/step - loss: 0.3082 - tp: 15953.0000 - fp: 1450.0000 - tn: 18984.0000 - fn: 4573.0000 - accuracy: 0.8530 - precision: 0.9167 - recall: 0.7772 - auc: 0.9327 - prc: 0.9487 - val_loss: 0.1903 - val_tp: 63.0000 - val_fp: 806.0000 - val_tn: 44694.0000 - val_fn: 6.0000 - val_accuracy: 0.9822 - val_precision: 0.0725 - val_recall: 0.9130 - val_auc: 0.9942 - val_prc: 0.7563 Epoch 15/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.2970 - tp: 15952.0000 - fp: 1287.0000 - tn: 19055.0000 - fn: 4666.0000 - accuracy: 0.8547 - precision: 0.9253 - recall: 0.7737 - auc: 0.9373 - prc: 0.9520 - val_loss: 0.1775 - val_tp: 63.0000 - val_fp: 774.0000 - val_tn: 44726.0000 - val_fn: 6.0000 - val_accuracy: 0.9829 - val_precision: 0.0753 - val_recall: 0.9130 - val_auc: 0.9949 - val_prc: 0.7595 Epoch 16/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.2834 - tp: 15633.0000 - fp: 1229.0000 - tn: 19595.0000 - fn: 4503.0000 - accuracy: 0.8601 - precision: 0.9271 - recall: 0.7764 - auc: 0.9431 - prc: 0.9542 - val_loss: 0.1665 - val_tp: 63.0000 - val_fp: 754.0000 - val_tn: 44746.0000 - val_fn: 6.0000 - val_accuracy: 0.9833 - val_precision: 0.0771 - val_recall: 0.9130 - val_auc: 0.9953 - val_prc: 0.7615 Epoch 17/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.2778 - tp: 15809.0000 - fp: 1186.0000 - tn: 19384.0000 - fn: 4581.0000 - accuracy: 0.8592 - precision: 0.9302 - recall: 0.7753 - auc: 0.9469 - prc: 0.9576 - val_loss: 0.1567 - val_tp: 63.0000 - val_fp: 738.0000 - val_tn: 44762.0000 - val_fn: 6.0000 - val_accuracy: 0.9837 - val_precision: 0.0787 - val_recall: 0.9130 - val_auc: 0.9957 - val_prc: 0.7651 Epoch 18/1000 20/20 [==============================] - 1s 30ms/step - loss: 0.2702 - tp: 15965.0000 - fp: 1113.0000 - tn: 19348.0000 - fn: 4534.0000 - accuracy: 0.8621 - precision: 0.9348 - recall: 0.7788 - auc: 0.9508 - prc: 0.9601 - val_loss: 0.1489 - val_tp: 63.0000 - val_fp: 738.0000 - val_tn: 44762.0000 - val_fn: 6.0000 - val_accuracy: 0.9837 - val_precision: 0.0787 - val_recall: 0.9130 - val_auc: 0.9960 - val_prc: 0.7679 Epoch 19/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.2586 - tp: 16031.0000 - fp: 1081.0000 - tn: 19414.0000 - fn: 4434.0000 - accuracy: 0.8654 - precision: 0.9368 - recall: 0.7833 - auc: 0.9553 - prc: 0.9633 - val_loss: 0.1420 - val_tp: 63.0000 - val_fp: 746.0000 - val_tn: 44754.0000 - val_fn: 6.0000 - val_accuracy: 0.9835 - val_precision: 0.0779 - val_recall: 0.9130 - val_auc: 0.9961 - val_prc: 0.7724 Epoch 20/1000 20/20 [==============================] - 1s 31ms/step - loss: 0.2562 - tp: 16026.0000 - fp: 1043.0000 - tn: 19414.0000 - fn: 4477.0000 - accuracy: 0.8652 - precision: 0.9389 - recall: 0.7816 - auc: 0.9569 - prc: 0.9641 - val_loss: 0.1360 - val_tp: 64.0000 - val_fp: 744.0000 - val_tn: 44756.0000 - val_fn: 5.0000 - val_accuracy: 0.9836 - val_precision: 0.0792 - val_recall: 0.9275 - val_auc: 0.9962 - val_prc: 0.7750 Epoch 21/1000 20/20 [==============================] - 1s 30ms/step - loss: 0.2461 - tp: 16002.0000 - fp: 1012.0000 - tn: 19574.0000 - fn: 4372.0000 - accuracy: 0.8686 - precision: 0.9405 - recall: 0.7854 - auc: 0.9604 - prc: 0.9667 - val_loss: 0.1305 - val_tp: 64.0000 - val_fp: 743.0000 - val_tn: 44757.0000 - val_fn: 5.0000 - val_accuracy: 0.9836 - val_precision: 0.0793 - val_recall: 0.9275 - val_auc: 0.9962 - val_prc: 0.7679 Epoch 22/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2421 - tp: 16160.0000 - fp: 973.0000 - tn: 19431.0000 - fn: 4396.0000 - accuracy: 0.8689 - precision: 0.9432 - recall: 0.7861 - auc: 0.9627 - prc: 0.9685 - val_loss: 0.1254 - val_tp: 64.0000 - val_fp: 743.0000 - val_tn: 44757.0000 - val_fn: 5.0000 - val_accuracy: 0.9836 - val_precision: 0.0793 - val_recall: 0.9275 - val_auc: 0.9962 - val_prc: 0.7700 Epoch 23/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.2362 - tp: 16012.0000 - fp: 998.0000 - tn: 19606.0000 - fn: 4344.0000 - accuracy: 0.8696 - precision: 0.9413 - recall: 0.7866 - auc: 0.9645 - prc: 0.9693 - val_loss: 0.1207 - val_tp: 65.0000 - val_fp: 744.0000 - val_tn: 44756.0000 - val_fn: 4.0000 - val_accuracy: 0.9836 - val_precision: 0.0803 - val_recall: 0.9420 - val_auc: 0.9962 - val_prc: 0.7720 Epoch 24/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2289 - tp: 16312.0000 - fp: 884.0000 - tn: 19492.0000 - fn: 4272.0000 - accuracy: 0.8741 - precision: 0.9486 - recall: 0.7925 - auc: 0.9675 - prc: 0.9719 - val_loss: 0.1163 - val_tp: 65.0000 - val_fp: 739.0000 - val_tn: 44761.0000 - val_fn: 4.0000 - val_accuracy: 0.9837 - val_precision: 0.0808 - val_recall: 0.9420 - val_auc: 0.9962 - val_prc: 0.7738 Epoch 25/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.2256 - tp: 16361.0000 - fp: 889.0000 - tn: 19458.0000 - fn: 4252.0000 - accuracy: 0.8745 - precision: 0.9485 - recall: 0.7937 - auc: 0.9690 - prc: 0.9730 - val_loss: 0.1134 - val_tp: 66.0000 - val_fp: 756.0000 - val_tn: 44744.0000 - val_fn: 3.0000 - val_accuracy: 0.9833 - val_precision: 0.0803 - val_recall: 0.9565 - val_auc: 0.9961 - val_prc: 0.7748 Epoch 26/1000 20/20 [==============================] - 1s 31ms/step - loss: 0.2208 - tp: 16267.0000 - fp: 893.0000 - tn: 19573.0000 - fn: 4227.0000 - accuracy: 0.8750 - precision: 0.9480 - recall: 0.7937 - auc: 0.9700 - prc: 0.9737 - val_loss: 0.1106 - val_tp: 66.0000 - val_fp: 762.0000 - val_tn: 44738.0000 - val_fn: 3.0000 - val_accuracy: 0.9832 - val_precision: 0.0797 - val_recall: 0.9565 - val_auc: 0.9961 - val_prc: 0.7758 Epoch 27/1000 20/20 [==============================] - 1s 34ms/step - loss: 0.2170 - tp: 16197.0000 - fp: 864.0000 - tn: 19723.0000 - fn: 4176.0000 - accuracy: 0.8770 - precision: 0.9494 - recall: 0.7950 - auc: 0.9717 - prc: 0.9745 - val_loss: 0.1082 - val_tp: 66.0000 - val_fp: 774.0000 - val_tn: 44726.0000 - val_fn: 3.0000 - val_accuracy: 0.9829 - val_precision: 0.0786 - val_recall: 0.9565 - val_auc: 0.9961 - val_prc: 0.7769 Epoch 28/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.2147 - tp: 16390.0000 - fp: 867.0000 - tn: 19544.0000 - fn: 4159.0000 - accuracy: 0.8773 - precision: 0.9498 - recall: 0.7976 - auc: 0.9721 - prc: 0.9754 - val_loss: 0.1051 - val_tp: 66.0000 - val_fp: 774.0000 - val_tn: 44726.0000 - val_fn: 3.0000 - val_accuracy: 0.9829 - val_precision: 0.0786 - val_recall: 0.9565 - val_auc: 0.9961 - val_prc: 0.7771 Epoch 29/1000 20/20 [==============================] - 1s 31ms/step - loss: 0.2100 - tp: 16237.0000 - fp: 868.0000 - tn: 19885.0000 - fn: 3970.0000 - accuracy: 0.8819 - precision: 0.9493 - recall: 0.8035 - auc: 0.9737 - prc: 0.9759 - val_loss: 0.1026 - val_tp: 66.0000 - val_fp: 785.0000 - val_tn: 44715.0000 - val_fn: 3.0000 - val_accuracy: 0.9827 - val_precision: 0.0776 - val_recall: 0.9565 - val_auc: 0.9960 - val_prc: 0.7781 Epoch 30/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.2117 - tp: 17870.0000 - fp: 1046.0000 - tn: 19512.0000 - fn: 2532.0000 - accuracy: 0.9126 - precision: 0.9447 - recall: 0.8759 - auc: 0.9734 - prc: 0.9757 - val_loss: 0.1003 - val_tp: 66.0000 - val_fp: 790.0000 - val_tn: 44710.0000 - val_fn: 3.0000 - val_accuracy: 0.9826 - val_precision: 0.0771 - val_recall: 0.9565 - val_auc: 0.9960 - val_prc: 0.7791 Epoch 31/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.2027 - tp: 18028.0000 - fp: 1001.0000 - tn: 19511.0000 - fn: 2420.0000 - accuracy: 0.9165 - precision: 0.9474 - recall: 0.8817 - auc: 0.9759 - prc: 0.9781 - val_loss: 0.0977 - val_tp: 66.0000 - val_fp: 782.0000 - val_tn: 44718.0000 - val_fn: 3.0000 - val_accuracy: 0.9828 - val_precision: 0.0778 - val_recall: 0.9565 - val_auc: 0.9959 - val_prc: 0.7807 Epoch 32/1000 20/20 [==============================] - 1s 29ms/step - loss: 0.2036 - tp: 18110.0000 - fp: 1003.0000 - tn: 19526.0000 - fn: 2321.0000 - accuracy: 0.9188 - precision: 0.9475 - recall: 0.8864 - auc: 0.9761 - prc: 0.9780 - val_loss: 0.0956 - val_tp: 66.0000 - val_fp: 789.0000 - val_tn: 44711.0000 - val_fn: 3.0000 - val_accuracy: 0.9826 - val_precision: 0.0772 - val_recall: 0.9565 - val_auc: 0.9959 - val_prc: 0.7723 Epoch 33/1000 20/20 [==============================] - ETA: 0s - loss: 0.2003 - tp: 18169.0000 - fp: 1012.0000 - tn: 19520.0000 - fn: 2259.0000 - accuracy: 0.9201 - precision: 0.9472 - recall: 0.8894 - auc: 0.9773 - prc: 0.9786Restoring model weights from the end of the best epoch: 23. 20/20 [==============================] - 1s 29ms/step - loss: 0.2003 - tp: 18169.0000 - fp: 1012.0000 - tn: 19520.0000 - fn: 2259.0000 - accuracy: 0.9201 - precision: 0.9472 - recall: 0.8894 - auc: 0.9773 - prc: 0.9786 - val_loss: 0.0931 - val_tp: 66.0000 - val_fp: 780.0000 - val_tn: 44720.0000 - val_fn: 3.0000 - val_accuracy: 0.9828 - val_precision: 0.0780 - val_recall: 0.9565 - val_auc: 0.9959 - val_prc: 0.7733 Epoch 33: early stopping
重新查看训练历史记录
plot_metrics(resampled_history)

评估指标
train_predictions_resampled = resampled_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_resampled = resampled_model.predict(test_features, batch_size=BATCH_SIZE)
90/90 [==============================] - 0s 1ms/step 28/28 [==============================] - 0s 1ms/step
resampled_results = resampled_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(resampled_model.metrics_names, resampled_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_resampled)
loss : 0.12108473479747772 tp : 95.0 fp : 915.0 tn : 55940.0 fn : 12.0 accuracy : 0.9837259650230408 precision : 0.09405940771102905 recall : 0.8878504633903503 auc : 0.9800193309783936 prc : 0.7522088289260864 Legitimate Transactions Detected (True Negatives): 55940 Legitimate Transactions Incorrectly Detected (False Positives): 915 Fraudulent Transactions Missed (False Negatives): 12 Fraudulent Transactions Detected (True Positives): 95 Total Fraudulent Transactions: 107

绘制 ROC
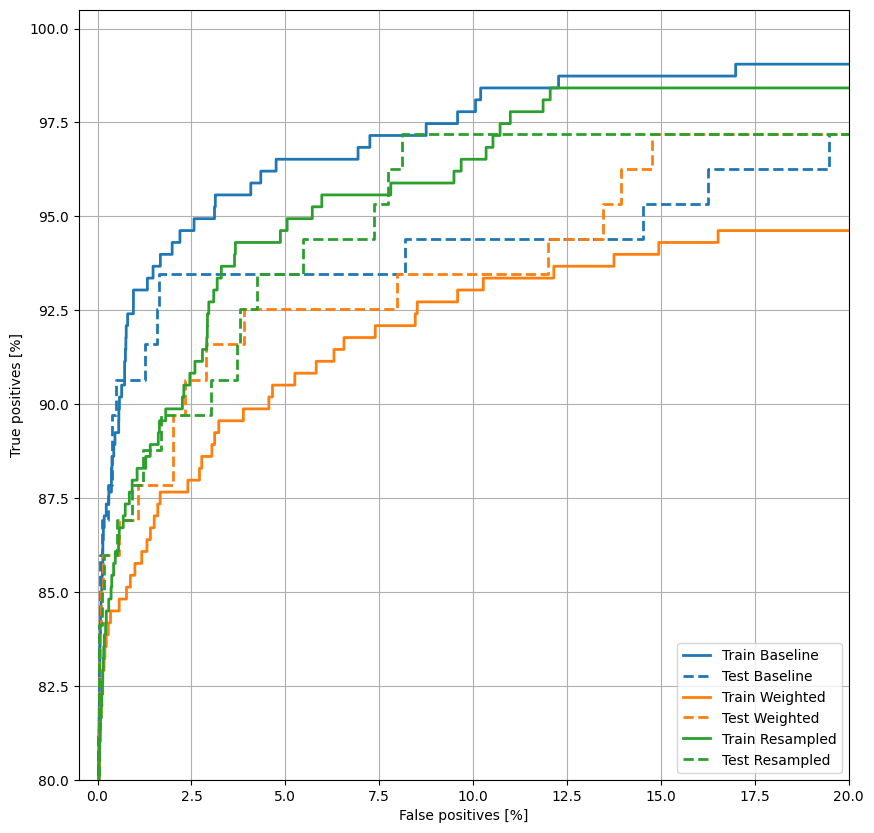
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_roc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_roc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');
绘制 AUPRC
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_prc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_prc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right');

使用本教程解决您的问题
由于可供学习的样本过少,不平衡数据的分类是固有难题。您应该始终先从数据开始,尽可能多地收集样本,并充分考虑可能相关的特征,以便模型能够充分利用占少数的类。有时您的模型可能难以改善且无法获得想要的结果,因此请务必牢记问题的上下文,并在不同类型的错误之间进行权衡。
