এই পৃষ্ঠাটি Cloud Translation API অনুবাদ করেছে।

টেন্সরফ্লো সম্ভাবনার একটি সফর

TensorFlow.org এ দেখুন

Google Colab-এ চালান

GitHub-এ উৎস দেখুন

নোটবুক ডাউনলোড করুন

এই Colab-এ আমরা TensorFlow সম্ভাব্যতার কিছু মৌলিক বৈশিষ্ট্য অন্বেষণ করি।

নির্ভরতা এবং পূর্বশর্ত

আমদানি

from pprint import pprint
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp

sns.reset_defaults()
sns.set_context(context='talk',font_scale=0.7)
plt.rcParams['image.cmap'] = 'viridis'

%matplotlib inline

tfd = tfp.distributions
tfb = tfp.bijectors

ইউটিলস

def print_subclasses_from_module(module, base_class, maxwidth=80):
  import functools, inspect, sys
  subclasses = [name for name, obj in inspect.getmembers(module)
                if inspect.isclass(obj) and issubclass(obj, base_class)]
  def red(acc, x):
    if not acc or len(acc[-1]) + len(x) + 2 > maxwidth:
      acc.append(x)
    else:
      acc[-1] += ", " + x
    return acc
  print('\n'.join(functools.reduce(red, subclasses, [])))

রূপরেখা

টেনসরফ্লো
টেনসরফ্লো সম্ভাবনা
- বিতরণ
- বিজেক্টর
- এমসিএমসি
- ...এবং আরো!

প্রস্তাবনা: টেনসরফ্লো

টেনসরফ্লো একটি বৈজ্ঞানিক কম্পিউটিং লাইব্রেরি।

এটা সমর্থন করে

প্রচুর গাণিতিক ক্রিয়াকলাপ
দক্ষ ভেক্টরাইজড গণনা
সহজ হার্ডওয়্যার ত্বরণ
স্বয়ংক্রিয় পার্থক্য

ভেক্টরাইজেশন

ভেক্টরাইজেশন জিনিসগুলি দ্রুত করে তোলে!
এর মানে আমরা আকার সম্পর্কে অনেক চিন্তা করি

mats = tf.random.uniform(shape=[1000, 10, 10])
vecs = tf.random.uniform(shape=[1000, 10, 1])

def for_loop_solve():
  return np.array(
    [tf.linalg.solve(mats[i, ...], vecs[i, ...]) for i in range(1000)])

def vectorized_solve():
  return tf.linalg.solve(mats, vecs)

# Vectorization for the win!
%timeit for_loop_solve()
%timeit vectorized_solve()

1 loops, best of 3: 2 s per loop
1000 loops, best of 3: 653 µs per loop

হার্ডওয়্যার ত্বরণ

# Code can run seamlessly on a GPU, just change Colab runtime type
# in the 'Runtime' menu.
if tf.test.gpu_device_name() == '/device:GPU:0':
  print("Using a GPU")
else:
  print("Using a CPU")

Using a CPU

স্বয়ংক্রিয় পার্থক্য

a = tf.constant(np.pi)
b = tf.constant(np.e)
with tf.GradientTape() as tape:
  tape.watch([a, b])
  c = .5 * (a**2 + b**2)
grads = tape.gradient(c, [a, b])
print(grads[0])
print(grads[1])

tf.Tensor(3.1415927, shape=(), dtype=float32)
tf.Tensor(2.7182817, shape=(), dtype=float32)

টেনসরফ্লো সম্ভাবনা

TensorFlow সম্ভাব্যতা হল TensorFlow-এ সম্ভাব্য যুক্তি এবং পরিসংখ্যানগত বিশ্লেষণের জন্য একটি লাইব্রেরি।

আমরা নিম্নস্তরের মডুলার উপাদান রচনা মাধ্যমে মডেলিং, ইনফারেন্স এবং সমালোচনা সমর্থন করি।

নিম্ন-স্তরের বিল্ডিং ব্লক

বিতরণ
বিজেক্টর

উচ্চ(er)-স্তরের নির্মাণ

মার্কভ চেইন মন্টে কার্লো
সম্ভাব্য স্তর
স্ট্রাকচারাল টাইম সিরিজ
সাধারণীকৃত লিনিয়ার মডেল
অপ্টিমাইজার

বিতরণ

একজন tfp.distributions.Distribution : দুই কোর পদ্ধতি সঙ্গে ক্লাস হয় sample এবং log_prob ।

টিএফপি অনেক বিতরণ করেছে!

print_subclasses_from_module(tfp.distributions, tfp.distributions.Distribution)

Autoregressive, BatchReshape, Bates, Bernoulli, Beta, BetaBinomial, Binomial
Blockwise, Categorical, Cauchy, Chi, Chi2, CholeskyLKJ, ContinuousBernoulli
Deterministic, Dirichlet, DirichletMultinomial, Distribution, DoublesidedMaxwell
Empirical, ExpGamma, ExpRelaxedOneHotCategorical, Exponential, FiniteDiscrete
Gamma, GammaGamma, GaussianProcess, GaussianProcessRegressionModel
GeneralizedNormal, GeneralizedPareto, Geometric, Gumbel, HalfCauchy, HalfNormal
HalfStudentT, HiddenMarkovModel, Horseshoe, Independent, InverseGamma
InverseGaussian, JohnsonSU, JointDistribution, JointDistributionCoroutine
JointDistributionCoroutineAutoBatched, JointDistributionNamed
JointDistributionNamedAutoBatched, JointDistributionSequential
JointDistributionSequentialAutoBatched, Kumaraswamy, LKJ, Laplace
LinearGaussianStateSpaceModel, LogLogistic, LogNormal, Logistic, LogitNormal
Mixture, MixtureSameFamily, Moyal, Multinomial, MultivariateNormalDiag
MultivariateNormalDiagPlusLowRank, MultivariateNormalFullCovariance
MultivariateNormalLinearOperator, MultivariateNormalTriL
MultivariateStudentTLinearOperator, NegativeBinomial, Normal, OneHotCategorical
OrderedLogistic, PERT, Pareto, PixelCNN, PlackettLuce, Poisson
PoissonLogNormalQuadratureCompound, PowerSpherical, ProbitBernoulli
QuantizedDistribution, RelaxedBernoulli, RelaxedOneHotCategorical, Sample
SinhArcsinh, SphericalUniform, StudentT, StudentTProcess
TransformedDistribution, Triangular, TruncatedCauchy, TruncatedNormal, Uniform
VariationalGaussianProcess, VectorDeterministic, VonMises
VonMisesFisher, Weibull, WishartLinearOperator, WishartTriL, Zipf

একটি সরল স্কালে-variate `Distribution`

# A standard normal
normal = tfd.Normal(loc=0., scale=1.)
print(normal)

tfp.distributions.Normal("Normal", batch_shape=[], event_shape=[], dtype=float32)

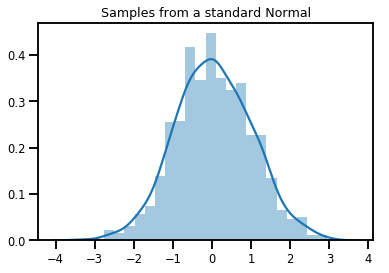
# Plot 1000 samples from a standard normal
samples = normal.sample(1000)
sns.distplot(samples)
plt.title("Samples from a standard Normal")
plt.show()

png

# Compute the log_prob of a point in the event space of `normal`
normal.log_prob(0.)

<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>

# Compute the log_prob of a few points
normal.log_prob([-1., 0., 1.])

<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.4189385, -0.9189385, -1.4189385], dtype=float32)>

বিতরণ এবং আকার

Numpy ndarrays এবং TensorFlow Tensors আকার আছে।

TensorFlow সম্ভাব্যতা Distributions যদিও মেমরি একই খণ্ড (শব্দার্থগতভাবে স্বতন্ত্র টুকরা আমরা পার্টিশন আকার, - আকৃতি শব্দার্থবিদ্যা আছে Tensor / ndarray ) পুরো সব কিছুর জন্য ব্যবহার করা হয়।

ব্যাচ আকৃতি একটি সংগ্রহ বোঝায় Distribution স্বতন্ত্র পরামিতি সঙ্গে গুলি
ইভেন্ট আকৃতি থেকে নমুনা আকৃতি উল্লেখ করে Distribution ।

আমরা সর্বদা "বামে" ব্যাচের আকার রাখি এবং "ডানদিকে" ইভেন্টের আকার রাখি।

স্কালে-variate একটি ব্যাচ `Distributions`

ব্যাচগুলি "ভেক্টরাইজড" বিতরণের মতো: স্বাধীন দৃষ্টান্ত যার গণনা সমান্তরালভাবে ঘটে।

# Create a batch of 3 normals, and plot 1000 samples from each
normals = tfd.Normal([-2.5, 0., 2.5], 1.)  # The scale parameter broadacasts!
print("Batch shape:", normals.batch_shape)
print("Event shape:", normals.event_shape)

Batch shape: (3,)
Event shape: ()

# Samples' shapes go on the left!
samples = normals.sample(1000)
print("Shape of samples:", samples.shape)

Shape of samples: (1000, 3)

# Sample shapes can themselves be more complicated
print("Shape of samples:", normals.sample([10, 10, 10]).shape)

Shape of samples: (10, 10, 10, 3)

# A batch of normals gives a batch of log_probs.
print(normals.log_prob([-2.5, 0., 2.5]))

tf.Tensor([-0.9189385 -0.9189385 -0.9189385], shape=(3,), dtype=float32)

# The computation broadcasts, so a batch of normals applied to a scalar
# also gives a batch of log_probs.
print(normals.log_prob(0.))

tf.Tensor([-4.0439386 -0.9189385 -4.0439386], shape=(3,), dtype=float32)

# Normal numpy-like broadcasting rules apply!
xs = np.linspace(-6, 6, 200)
try:
  normals.log_prob(xs)
except Exception as e:
  print("TFP error:", e.message)

TFP error: Incompatible shapes: [200] vs. [3] [Op:SquaredDifference]

# That fails for the same reason this does:
try:
  np.zeros(200) + np.zeros(3)
except Exception as e:
  print("Numpy error:", e)

Numpy error: operands could not be broadcast together with shapes (200,) (3,)

# But this would work:
a = np.zeros([200, 1]) + np.zeros(3)
print("Broadcast shape:", a.shape)

Broadcast shape: (200, 3)

# And so will this!
xs = np.linspace(-6, 6, 200)[..., np.newaxis]
# => shape = [200, 1]

lps = normals.log_prob(xs)
print("Broadcast log_prob shape:", lps.shape)

Broadcast log_prob shape: (200, 3)

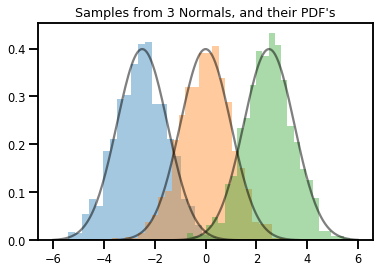
# Summarizing visually
for i in range(3):
  sns.distplot(samples[:, i], kde=False, norm_hist=True)
plt.plot(np.tile(xs, 3), normals.prob(xs), c='k', alpha=.5)
plt.title("Samples from 3 Normals, and their PDF's")
plt.show()

png

একটি ভেক্টর-variate `Distribution`

mvn = tfd.MultivariateNormalDiag(loc=[0., 0.], scale_diag = [1., 1.])
print("Batch shape:", mvn.batch_shape)
print("Event shape:", mvn.event_shape)

Batch shape: ()
Event shape: (2,)

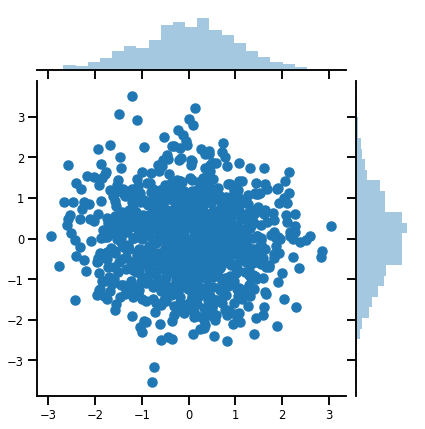
samples = mvn.sample(1000)
print("Samples shape:", samples.shape)

Samples shape: (1000, 2)

g = sns.jointplot(samples[:, 0], samples[:, 1], kind='scatter')
plt.show()

png

একটি ম্যাট্রিক্স-variate `Distribution`

lkj = tfd.LKJ(dimension=10, concentration=[1.5, 3.0])
print("Batch shape: ", lkj.batch_shape)
print("Event shape: ", lkj.event_shape)

Batch shape:  (2,)
Event shape:  (10, 10)

samples = lkj.sample()
print("Samples shape: ", samples.shape)

Samples shape:  (2, 10, 10)

fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(6, 3))
sns.heatmap(samples[0, ...], ax=axes[0], cbar=False)
sns.heatmap(samples[1, ...], ax=axes[1], cbar=False)
fig.tight_layout()
plt.show()

png

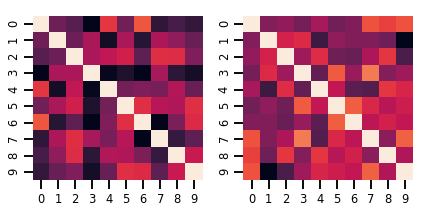
গাউসিয়ান প্রসেস

kernel = tfp.math.psd_kernels.ExponentiatedQuadratic()
xs = np.linspace(-5., 5., 200).reshape([-1, 1])
gp = tfd.GaussianProcess(kernel, index_points=xs)
print("Batch shape:", gp.batch_shape)
print("Event shape:", gp.event_shape)

Batch shape: ()
Event shape: (200,)

upper, lower = gp.mean() + [2 * gp.stddev(), -2 * gp.stddev()]
plt.plot(xs, gp.mean())
plt.fill_between(xs[..., 0], upper, lower, color='k', alpha=.1)
for _ in range(5):
  plt.plot(xs, gp.sample(), c='r', alpha=.3)
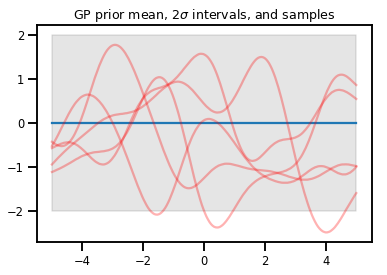
plt.title(r"GP prior mean, $2\sigma$ intervals, and samples")
plt.show()

#    *** Bonus question ***
# Why do so many of these functions lie outside the 95% intervals?

png

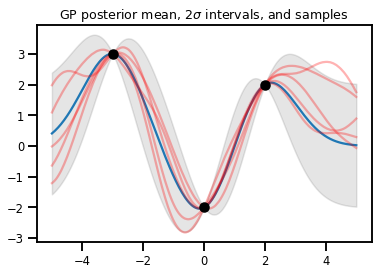
জিপি রিগ্রেশন

# Suppose we have some observed data
obs_x = [[-3.], [0.], [2.]]  # Shape 3x1 (3 1-D vectors)
obs_y = [3., -2., 2.]        # Shape 3   (3 scalars)

gprm = tfd.GaussianProcessRegressionModel(kernel, xs, obs_x, obs_y)

upper, lower = gprm.mean() + [2 * gprm.stddev(), -2 * gprm.stddev()]
plt.plot(xs, gprm.mean())
plt.fill_between(xs[..., 0], upper, lower, color='k', alpha=.1)
for _ in range(5):
  plt.plot(xs, gprm.sample(), c='r', alpha=.3)
plt.scatter(obs_x, obs_y, c='k', zorder=3)
plt.title(r"GP posterior mean, $2\sigma$ intervals, and samples")
plt.show()

png

বিজেক্টর

বিজেক্টর প্রতিনিধিত্ব করে (বেশিরভাগ) ইনভার্টেবল, মসৃণ ফাংশন। এগুলি বিতরণগুলিকে রূপান্তর করতে ব্যবহার করা যেতে পারে, নমুনা নেওয়ার এবং log_probs গণনা করার ক্ষমতা সংরক্ষণ করে। তারা হতে পারে tfp.bijectors মডিউল।

প্রতিটি বিজেক্টর কমপক্ষে 3টি পদ্ধতি প্রয়োগ করে:

forward ,
inverse , এবং
(অন্তত) এক forward_log_det_jacobian এবং inverse_log_det_jacobian ।

এই উপাদানগুলির সাহায্যে, আমরা একটি বিতরণকে রূপান্তর করতে পারি এবং এখনও ফলাফল থেকে নমুনা এবং লগ প্রোব পেতে পারি!

গণিত, কিছুটা sloppily

\(X\) পিডিএফ সঙ্গে একটি র্যান্ডম পরিবর্তনশীল \(p(x)\)
\(g\) স্থান উপর একটি নির্ঝঞ্চাট, একটি নির্দিষ্ট ফাংশন \(X\)এর
\(Y = g(X)\) একটি নতুন, রুপান্তরিত র্যান্ডম পরিবর্তনশীল
\(p(Y=y) = p(X=g^{-1}(y)) \cdot |\nabla g^{-1}(y)|\)

ক্যাশিং

বিজেক্টরগুলি ফরোয়ার্ড এবং ইনভার্স কম্পিউটেশন এবং লগ-ডেট-জ্যাকোবিয়ানসকেও ক্যাশে করে, যা আমাদেরকে সম্ভাব্য অত্যন্ত ব্যয়বহুল অপারেশনগুলিকে পুনরাবৃত্তি করার অনুমতি দেয়!

print_subclasses_from_module(tfp.bijectors, tfp.bijectors.Bijector)

AbsoluteValue, Affine, AffineLinearOperator, AffineScalar, BatchNormalization
Bijector, Blockwise, Chain, CholeskyOuterProduct, CholeskyToInvCholesky
CorrelationCholesky, Cumsum, DiscreteCosineTransform, Exp, Expm1, FFJORD
FillScaleTriL, FillTriangular, FrechetCDF, GeneralizedExtremeValueCDF
GeneralizedPareto, GompertzCDF, GumbelCDF, Identity, Inline, Invert
IteratedSigmoidCentered, KumaraswamyCDF, LambertWTail, Log, Log1p
MaskedAutoregressiveFlow, MatrixInverseTriL, MatvecLU, MoyalCDF, NormalCDF
Ordered, Pad, Permute, PowerTransform, RationalQuadraticSpline, RayleighCDF
RealNVP, Reciprocal, Reshape, Scale, ScaleMatvecDiag, ScaleMatvecLU
ScaleMatvecLinearOperator, ScaleMatvecTriL, ScaleTriL, Shift, ShiftedGompertzCDF
Sigmoid, Sinh, SinhArcsinh, SoftClip, Softfloor, SoftmaxCentered, Softplus
Softsign, Split, Square, Tanh, TransformDiagonal, Transpose, WeibullCDF

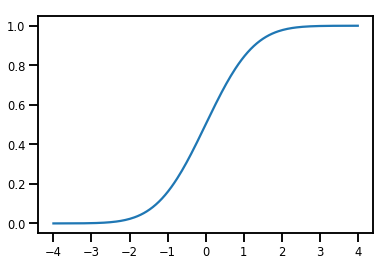
একটি সহজ `Bijector`

normal_cdf = tfp.bijectors.NormalCDF()
xs = np.linspace(-4., 4., 200)
plt.plot(xs, normal_cdf.forward(xs))
plt.show()

png

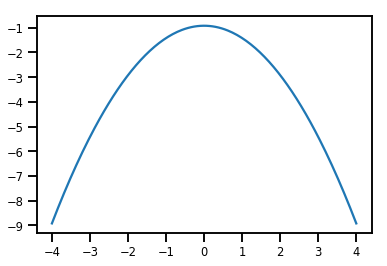
plt.plot(xs, normal_cdf.forward_log_det_jacobian(xs, event_ndims=0))
plt.show()

png

একজন `Bijector` একটি রূপান্তর `Distribution`

exp_bijector = tfp.bijectors.Exp()
log_normal = exp_bijector(tfd.Normal(0., .5))

samples = log_normal.sample(1000)
xs = np.linspace(1e-10, np.max(samples), 200)
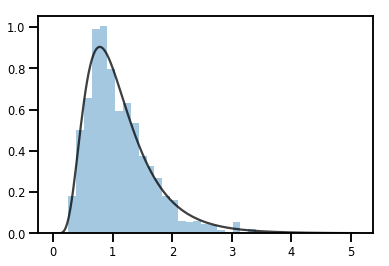
sns.distplot(samples, norm_hist=True, kde=False)
plt.plot(xs, log_normal.prob(xs), c='k', alpha=.75)
plt.show()

png

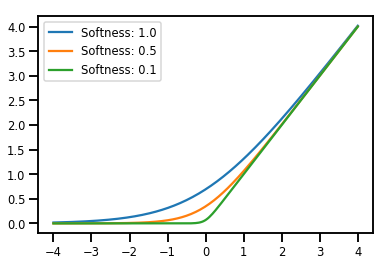
ছোট্ট `Bijectors`

# Create a batch of bijectors of shape [3,]
softplus = tfp.bijectors.Softplus(
  hinge_softness=[1., .5, .1])
print("Hinge softness shape:", softplus.hinge_softness.shape)

Hinge softness shape: (3,)

# For broadcasting, we want this to be shape [200, 1]
xs = np.linspace(-4., 4., 200)[..., np.newaxis]
ys = softplus.forward(xs)
print("Forward shape:", ys.shape)

Forward shape: (200, 3)

# Visualization
lines = plt.plot(np.tile(xs, 3), ys)
for line, hs in zip(lines, softplus.hinge_softness):
  line.set_label("Softness: %1.1f" % hs)
plt.legend()
plt.show()

png

ক্যাশিং

# This bijector represents a matrix outer product on the forward pass,
# and a cholesky decomposition on the inverse pass. The latter costs O(N^3)!
bij = tfb.CholeskyOuterProduct()

size = 2500
# Make a big, lower-triangular matrix
big_lower_triangular = tf.eye(size)
# Squaring it gives us a positive-definite matrix
big_positive_definite = bij.forward(big_lower_triangular)

# Caching for the win!
%timeit bij.inverse(big_positive_definite)
%timeit tf.linalg.cholesky(big_positive_definite)

10000 loops, best of 3: 114 µs per loop
1 loops, best of 3: 208 ms per loop

এমসিএমসি

TFP হ্যামিলটোনিয়ান মন্টে কার্লো সহ কিছু স্ট্যান্ডার্ড মার্কভ চেইন মন্টে কার্লো অ্যালগরিদমের সমর্থনে তৈরি করেছে।

একটি ডেটা সেট তৈরি করুন

# Generate some data
def f(x, w):
  # Pad x with 1's so we can add bias via matmul
  x = tf.pad(x, [[1, 0], [0, 0]], constant_values=1)
  linop = tf.linalg.LinearOperatorFullMatrix(w[..., np.newaxis])
  result = linop.matmul(x, adjoint=True)
  return result[..., 0, :]

num_features = 2
num_examples = 50
noise_scale = .5
true_w = np.array([-1., 2., 3.])

xs = np.random.uniform(-1., 1., [num_features, num_examples])
ys = f(xs, true_w) + np.random.normal(0., noise_scale, size=num_examples)

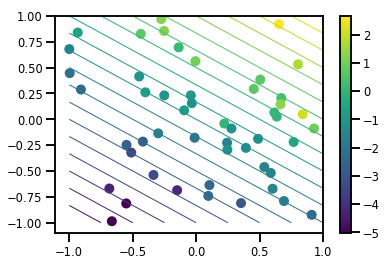
# Visualize the data set
plt.scatter(*xs, c=ys, s=100, linewidths=0)

grid = np.meshgrid(*([np.linspace(-1, 1, 100)] * 2))
xs_grid = np.stack(grid, axis=0)
fs_grid = f(xs_grid.reshape([num_features, -1]), true_w)
fs_grid = np.reshape(fs_grid, [100, 100])
plt.colorbar()
plt.contour(xs_grid[0, ...], xs_grid[1, ...], fs_grid, 20, linewidths=1)
plt.show()

png

আমাদের জয়েন্ট লগ-প্রব ফাংশন সংজ্ঞায়িত করুন

Unnormalized অবর ডেটার উপর বন্ধের একটি গঠনের ফলাফল আংশিক আবেদন যৌথ লগ PROB করুন।

# Define the joint_log_prob function, and our unnormalized posterior.
def joint_log_prob(w, x, y):
  # Our model in maths is
  #   w ~ MVN([0, 0, 0], diag([1, 1, 1]))
  #   y_i ~ Normal(w @ x_i, noise_scale),  i=1..N

  rv_w = tfd.MultivariateNormalDiag(
    loc=np.zeros(num_features + 1),
    scale_diag=np.ones(num_features + 1))

  rv_y = tfd.Normal(f(x, w), noise_scale)
  return (rv_w.log_prob(w) +
          tf.reduce_sum(rv_y.log_prob(y), axis=-1))

# Create our unnormalized target density by currying x and y from the joint.
def unnormalized_posterior(w):
  return joint_log_prob(w, xs, ys)

HMC TransitionKernel তৈরি করুন এবং স্যাম্পল_চেইন কল করুন

# Create an HMC TransitionKernel
hmc_kernel = tfp.mcmc.HamiltonianMonteCarlo(
  target_log_prob_fn=unnormalized_posterior,
  step_size=np.float64(.1),
  num_leapfrog_steps=2)

# We wrap sample_chain in tf.function, telling TF to precompile a reusable
# computation graph, which will dramatically improve performance.
@tf.function
def run_chain(initial_state, num_results=1000, num_burnin_steps=500):
  return tfp.mcmc.sample_chain(
    num_results=num_results,
    num_burnin_steps=num_burnin_steps,
    current_state=initial_state,
    kernel=hmc_kernel,
    trace_fn=lambda current_state, kernel_results: kernel_results)

initial_state = np.zeros(num_features + 1)
samples, kernel_results = run_chain(initial_state)
print("Acceptance rate:", kernel_results.is_accepted.numpy().mean())

Acceptance rate: 0.915

যে মহান না! আমরা .65 এর কাছাকাছি একটি গ্রহণযোগ্যতা হার চাই।

(দেখুন "বিভিন্ন মহানগরী-হেস্টিংস আলগোরিদিম জন্য সর্বাপেক্ষা কাম্য স্কেলিং" , রবার্টস ও Rosenthal, 2001)

অভিযোজিত ধাপ মাপ

আমরা একটি আমাদের ক্ষেত্রে HMC TransitionKernel মোড়ানো পারেন SimpleStepSizeAdaptation "মেটা-কার্নেল", যা কিছু (বরং সহজ অনুসন্ধানমূলক) যুক্তিবিজ্ঞান Burnin সময় ক্ষেত্রে HMC ধাপে আকার খাপ খাওয়ানো প্রয়োগ করা হবে। আমরা ধাপের আকার মানিয়ে নেওয়ার জন্য 80% বার্নিন বরাদ্দ করি, এবং তারপরে অবশিষ্ট 20% শুধুমাত্র মিশ্রণে যেতে দিন।

# Apply a simple step size adaptation during burnin
@tf.function
def run_chain(initial_state, num_results=1000, num_burnin_steps=500):
  adaptive_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      hmc_kernel,
      num_adaptation_steps=int(.8 * num_burnin_steps),
      target_accept_prob=np.float64(.65))

  return tfp.mcmc.sample_chain(
    num_results=num_results,
    num_burnin_steps=num_burnin_steps,
    current_state=initial_state,
    kernel=adaptive_kernel,
    trace_fn=lambda cs, kr: kr)

samples, kernel_results = run_chain(
  initial_state=np.zeros(num_features+1))
print("Acceptance rate:", kernel_results.inner_results.is_accepted.numpy().mean())

Acceptance rate: 0.634

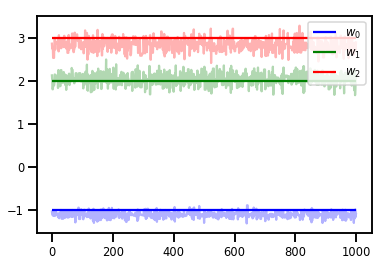
# Trace plots
colors = ['b', 'g', 'r']
for i in range(3):
  plt.plot(samples[:, i], c=colors[i], alpha=.3)
  plt.hlines(true_w[i], 0, 1000, zorder=4, color=colors[i], label="$w_{}$".format(i))
plt.legend(loc='upper right')
plt.show()

# Histogram of samples
for i in range(3):
  sns.distplot(samples[:, i], color=colors[i])
ymax = plt.ylim()[1]
for i in range(3):
  plt.vlines(true_w[i], 0, ymax, color=colors[i])
plt.ylim(0, ymax)
plt.show()

png

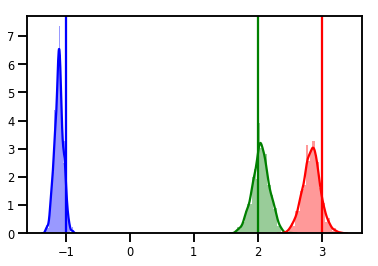
কারণ নির্ণয়

ট্রেস প্লট সুন্দর, কিন্তু ডায়াগনস্টিক সুন্দর!

প্রথমে আমাদের একাধিক চেইন চালাতে হবে। এই একটি ব্যাচ দান হিসাবে সহজ হিসাবে initial_state tensors।

# Instead of a single set of initial w's, we create a batch of 8.
num_chains = 8
initial_state = np.zeros([num_chains, num_features + 1])

chains, kernel_results = run_chain(initial_state)

r_hat = tfp.mcmc.potential_scale_reduction(chains)
print("Acceptance rate:", kernel_results.inner_results.is_accepted.numpy().mean())
print("R-hat diagnostic (per latent variable):", r_hat.numpy())

Acceptance rate: 0.59175
R-hat diagnostic (per latent variable): [0.99998395 0.99932185 0.9997064 ]

শব্দ স্কেল নমুনা

# Define the joint_log_prob function, and our unnormalized posterior.
def joint_log_prob(w, sigma, x, y):
  # Our model in maths is
  #   w ~ MVN([0, 0, 0], diag([1, 1, 1]))
  #   y_i ~ Normal(w @ x_i, noise_scale),  i=1..N

  rv_w = tfd.MultivariateNormalDiag(
    loc=np.zeros(num_features + 1),
    scale_diag=np.ones(num_features + 1))

  rv_sigma = tfd.LogNormal(np.float64(1.), np.float64(5.))

  rv_y = tfd.Normal(f(x, w), sigma[..., np.newaxis])
  return (rv_w.log_prob(w) +
          rv_sigma.log_prob(sigma) +
          tf.reduce_sum(rv_y.log_prob(y), axis=-1))

# Create our unnormalized target density by currying x and y from the joint.
def unnormalized_posterior(w, sigma):
  return joint_log_prob(w, sigma, xs, ys)


# Create an HMC TransitionKernel
hmc_kernel = tfp.mcmc.HamiltonianMonteCarlo(
  target_log_prob_fn=unnormalized_posterior,
  step_size=np.float64(.1),
  num_leapfrog_steps=4)



# Create a TransformedTransitionKernl
transformed_kernel = tfp.mcmc.TransformedTransitionKernel(
    inner_kernel=hmc_kernel,
    bijector=[tfb.Identity(),    # w
              tfb.Invert(tfb.Softplus())])   # sigma


# Apply a simple step size adaptation during burnin
@tf.function
def run_chain(initial_state, num_results=1000, num_burnin_steps=500):
  adaptive_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      transformed_kernel,
      num_adaptation_steps=int(.8 * num_burnin_steps),
      target_accept_prob=np.float64(.75))

  return tfp.mcmc.sample_chain(
    num_results=num_results,
    num_burnin_steps=num_burnin_steps,
    current_state=initial_state,
    kernel=adaptive_kernel,
    seed=(0, 1),
    trace_fn=lambda cs, kr: kr)


# Instead of a single set of initial w's, we create a batch of 8.
num_chains = 8
initial_state = [np.zeros([num_chains, num_features + 1]),
                 .54 * np.ones([num_chains], dtype=np.float64)]

chains, kernel_results = run_chain(initial_state)

r_hat = tfp.mcmc.potential_scale_reduction(chains)
print("Acceptance rate:", kernel_results.inner_results.inner_results.is_accepted.numpy().mean())
print("R-hat diagnostic (per w variable):", r_hat[0].numpy())
print("R-hat diagnostic (sigma):", r_hat[1].numpy())

Acceptance rate: 0.715875
R-hat diagnostic (per w variable): [1.0000073  1.00458208 1.00450512]
R-hat diagnostic (sigma): 1.0092056996149859

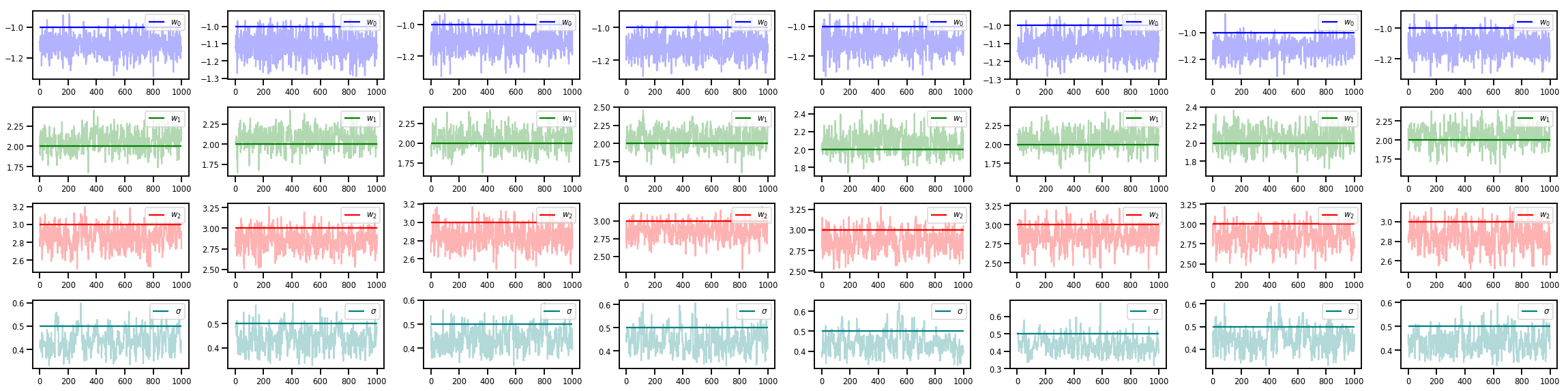
w_chains, sigma_chains = chains

# Trace plots of w (one of 8 chains)
colors = ['b', 'g', 'r', 'teal']
fig, axes = plt.subplots(4, num_chains, figsize=(4 * num_chains, 8))
for j in range(num_chains):
  for i in range(3):
    ax = axes[i][j]
    ax.plot(w_chains[:, j, i], c=colors[i], alpha=.3)
    ax.hlines(true_w[i], 0, 1000, zorder=4, color=colors[i], label="$w_{}$".format(i))
    ax.legend(loc='upper right')
  ax = axes[3][j]
  ax.plot(sigma_chains[:, j], alpha=.3, c=colors[3])
  ax.hlines(noise_scale, 0, 1000, zorder=4, color=colors[3], label=r"$\sigma$".format(i))
  ax.legend(loc='upper right')
fig.tight_layout()
plt.show()

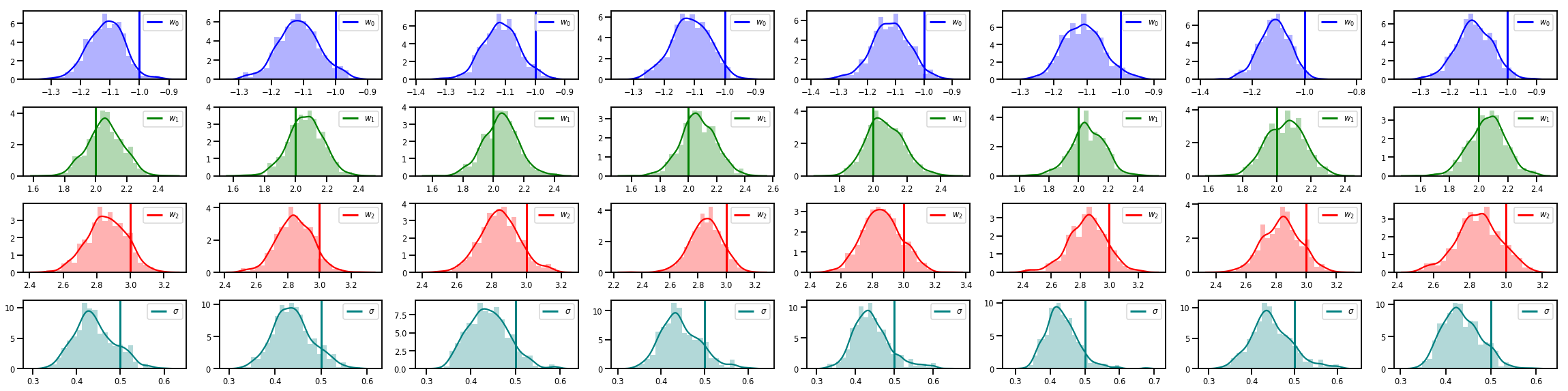
# Histogram of samples of w
fig, axes = plt.subplots(4, num_chains, figsize=(4 * num_chains, 8))
for j in range(num_chains):
  for i in range(3):
    ax = axes[i][j]
    sns.distplot(w_chains[:, j, i], color=colors[i], norm_hist=True, ax=ax, hist_kws={'alpha': .3})
  for i in range(3):
    ax = axes[i][j]
    ymax = ax.get_ylim()[1]
    ax.vlines(true_w[i], 0, ymax, color=colors[i], label="$w_{}$".format(i), linewidth=3)
    ax.set_ylim(0, ymax)
    ax.legend(loc='upper right')


  ax = axes[3][j]
  sns.distplot(sigma_chains[:, j], color=colors[3], norm_hist=True, ax=ax, hist_kws={'alpha': .3})
  ymax = ax.get_ylim()[1]
  ax.vlines(noise_scale, 0, ymax, color=colors[3], label=r"$\sigma$".format(i), linewidth=3)
  ax.set_ylim(0, ymax)
  ax.legend(loc='upper right')
fig.tight_layout()
plt.show()

png

আরো অনেক কিছু আছে!

এই দুর্দান্ত ব্লগ পোস্ট এবং উদাহরণগুলি দেখুন:

কাঠামোগত টাইম সিরিজ সমর্থন ব্লগ colab
সম্ভাব্য Keras স্তরসমূহ (ইনপুট: টেন্সর, আউটপুট: বিতরণ!) ব্লগ colab
- আরেকটি স্তরসমূহ উদাহরণ: VAEs ব্লগ colab
গসিয়ান প্রক্রিয়া রিগ্রেশন colab এবং প্রচ্ছন্ন চলক মডেলিং colab

আরো উদাহরণ এবং আমাদের GitHub থেকে নোটবুক এখানে !

টেন্সরফ্লো সম্ভাবনার একটি সফর

নির্ভরতা এবং পূর্বশর্ত

আমদানি

ইউটিলস

রূপরেখা

প্রস্তাবনা: টেনসরফ্লো

ভেক্টরাইজেশন

হার্ডওয়্যার ত্বরণ

স্বয়ংক্রিয় পার্থক্য

টেনসরফ্লো সম্ভাবনা

নিম্ন-স্তরের বিল্ডিং ব্লক

উচ্চ(er)-স্তরের নির্মাণ

বিতরণ

একটি সরল স্কালে-variate Distribution

বিতরণ এবং আকার

স্কালে-variate একটি ব্যাচ Distributions

একটি ভেক্টর-variate Distribution

একটি ম্যাট্রিক্স-variate Distribution

গাউসিয়ান প্রসেস

জিপি রিগ্রেশন

বিজেক্টর

গণিত, কিছুটা sloppily

ক্যাশিং

একটি সহজ Bijector

একজন Bijector একটি রূপান্তর Distribution

ছোট্ট Bijectors

ক্যাশিং

এমসিএমসি

একটি ডেটা সেট তৈরি করুন

আমাদের জয়েন্ট লগ-প্রব ফাংশন সংজ্ঞায়িত করুন

HMC TransitionKernel তৈরি করুন এবং স্যাম্পল_চেইন কল করুন

অভিযোজিত ধাপ মাপ

কারণ নির্ণয়

শব্দ স্কেল নমুনা

আরো অনেক কিছু আছে!

একটি সরল স্কালে-variate `Distribution`

স্কালে-variate একটি ব্যাচ `Distributions`

একটি ভেক্টর-variate `Distribution`

একটি ম্যাট্রিক্স-variate `Distribution`

একটি সহজ `Bijector`

একজন `Bijector` একটি রূপান্তর `Distribution`

ছোট্ট `Bijectors`