Lựa chọn mô hình Bayes
 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Nhập khẩu
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
Nhiệm vụ: phát hiện điểm thay đổi với nhiều điểm thay đổi
Xem xét nhiệm vụ phát hiện điểm thay đổi: các sự kiện xảy ra với tốc độ thay đổi theo thời gian, được thúc đẩy bởi sự thay đổi đột ngột trong trạng thái (không được quan sát) của một số hệ thống hoặc quy trình tạo ra dữ liệu.
Ví dụ, chúng ta có thể quan sát thấy một loạt các số đếm như sau:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
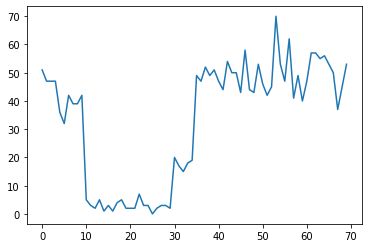
Chúng có thể đại diện cho số lỗi trong một trung tâm dữ liệu, số lượng khách truy cập vào một trang web, số lượng gói trên một liên kết mạng, v.v.
Lưu ý rằng không hoàn toàn rõ ràng có bao nhiêu chế độ hệ thống riêng biệt chỉ khi nhìn vào dữ liệu. Bạn có thể cho biết vị trí của mỗi điểm trong số ba điểm chuyển mạch?
Số trạng thái đã biết
Đầu tiên chúng ta sẽ xem xét trường hợp (có lẽ không thực tế) trong đó số lượng trạng thái không được quan sát được biết là tiên nghiệm. Ở đây, chúng tôi giả sử rằng chúng tôi biết có bốn trạng thái tiềm ẩn.
Chúng tôi mô hình vấn đề này như một chuyển mạch (không đồng nhất) quá trình Poisson: tại mỗi thời điểm, số lượng các sự kiện xảy ra là Poisson phân phối, và tỷ lệ của các sự kiện được xác định bởi quan sát được trạng thái hệ thống \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
Các trạng thái tiềm ẩn là rời rạc: \(z_t \in \{1, 2, 3, 4\}\), vì vậy \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) là một vector đơn giản có chứa một tỷ lệ Poisson cho mỗi tiểu bang. Để mô hình sự tiến hóa của các quốc gia theo thời gian, chúng tôi sẽ xác định một đơn giản mô hình chuyển \(p(z_t | z_{t-1})\): giả sử rằng tại mỗi bước chúng ta ở trong trạng thái trước đó với một số khả năng \(p\), và với xác suất \(1-p\) chúng tôi chuyển đổi sang một trạng thái khác nhau đồng nhất một cách ngẫu nhiên. Trạng thái ban đầu cũng được chọn ngẫu nhiên một cách đồng nhất, vì vậy chúng ta có:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
Những giả định tương ứng với một mô hình Markov ẩn với lượng khí thải Poisson. Chúng tôi có thể mã hóa chúng trong TFP sử dụng tfd.HiddenMarkovModel . Đầu tiên, chúng tôi xác định ma trận chuyển tiếp và ma trận đồng nhất trước ở trạng thái ban đầu:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
Tiếp theo, chúng ta xây dựng một tfd.HiddenMarkovModel phân phối, sử dụng một biến khả năng huấn luyện để đại diện cho tỷ lệ kết hợp với mỗi trạng thái hệ thống. Chúng tôi tham số hóa các tỷ lệ trong không gian log để đảm bảo chúng có giá trị dương.
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
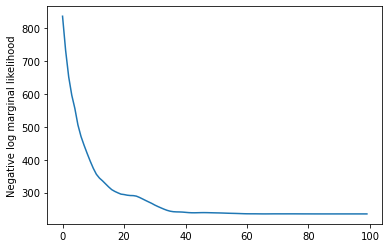
Cuối cùng, chúng ta định nghĩa tổng mật độ log của mô hình, trong đó có một lognormal yếu-thông tin trước về tỷ lệ, và chạy một ưu để tính toán tối đa một posteriori (MAP) phù hợp với các dữ liệu số quan sát được.
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
Nó đã làm việc! Lưu ý rằng các trạng thái tiềm ẩn trong mô hình này chỉ có thể xác định được cho đến khi hoán vị, vì vậy tỷ lệ chúng tôi khôi phục được theo một thứ tự khác và có một chút nhiễu, nhưng nhìn chung chúng khá khớp.
Khôi phục quỹ đạo trạng thái
Bây giờ chúng ta đã phù hợp với những mô hình, chúng ta có thể muốn tái tạo lại mà nhà nước mô hình tin hệ thống đang ở tại mỗi bước thời gian.
Đây là một nhiệm vụ suy luận sau: trao đếm quan sát \(x_{1:T}\) và các thông số mô hình (tỷ lệ) \(\lambda\), chúng tôi muốn suy ra chuỗi các biến ẩn rời rạc, sau khi phân bố sau \(p(z_{1:T} | x_{1:T}, \lambda)\). Trong một mô hình Markov ẩn, chúng tôi có thể tính toán hiệu quả các biên và các thuộc tính khác của phân phối này bằng cách sử dụng các thuật toán truyền thông điệp tiêu chuẩn. Đặc biệt, posterior_marginals phương pháp sẽ có hiệu quả tính toán (bằng cách sử dụng thuật toán chuyển tiếp-backward ) các biên phân bố xác suất \(p(Z_t = z_t | x_{1:T})\) trong trạng thái tiềm ẩn rời rạc \(Z_t\) tại mỗi bước thời gian \(t\).
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
Lập đồ thị các xác suất sau, chúng tôi khôi phục "lời giải thích" của mô hình về dữ liệu: mỗi trạng thái hoạt động tại những thời điểm nào?
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
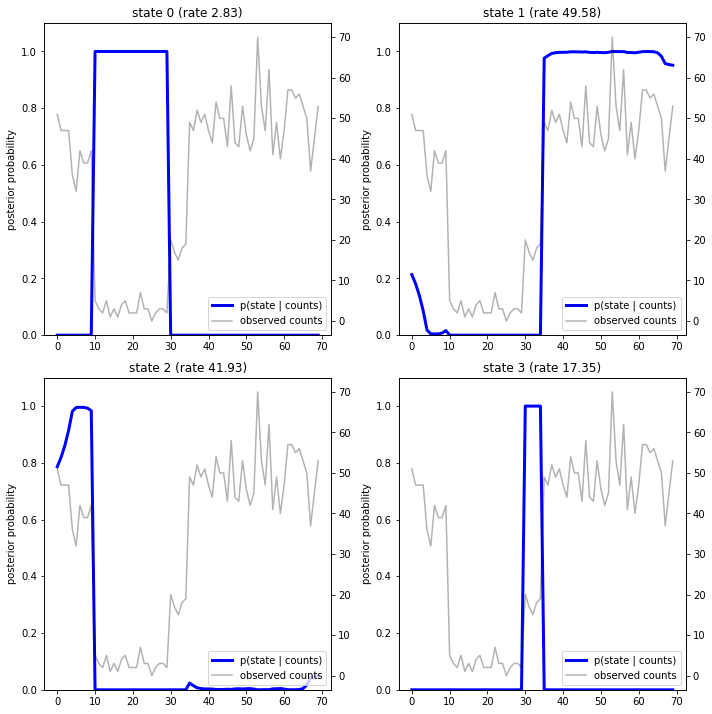
Trong trường hợp (đơn giản) này, chúng ta thấy rằng mô hình thường khá tự tin: ở hầu hết các bước thời gian, nó chỉ định cơ bản tất cả khối lượng xác suất cho một trong bốn trạng thái. May mắn thay, những lời giải thích có vẻ hợp lý!
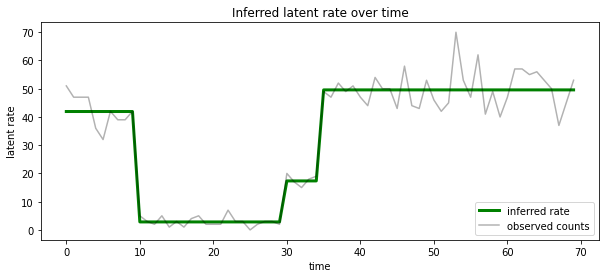
Chúng tôi cũng có thể hình dung sau này về tỷ lệ liên quan đến tình trạng tiềm ẩn khả năng nhất tại mỗi bước thời gian, ngưng tụ hậu xác suất thành một lời giải thích duy nhất:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
Số trạng thái không xác định
Trong các vấn đề thực tế, chúng tôi có thể không biết số trạng thái 'thực sự' trong hệ thống mà chúng tôi đang mô hình hóa. Điều này có thể không phải lúc nào cũng đáng lo ngại: nếu bạn không đặc biệt quan tâm đến danh tính của các trạng thái chưa biết, bạn có thể chỉ chạy một mô hình có nhiều trạng thái hơn mức bạn biết mô hình sẽ cần và tìm hiểu (đại loại như) một loạt các bản sao bản sao của các trạng thái thực tế. Nhưng giả sử bạn quan tâm đến việc suy ra số trạng thái tiềm ẩn 'thực sự'.
Chúng ta có thể xem đây là một trường hợp lựa chọn mô hình Bayes : chúng ta có một tập hợp các mô hình ứng cử viên, đều có một số khác nhau của các quốc gia tiềm ẩn, và chúng tôi muốn chọn một trong đó là rất có thể đã tạo ra các dữ liệu quan sát được. Để làm điều này, chúng tôi tính toán khả năng biên của các dữ liệu theo từng mô hình (chúng tôi cũng có thể thêm một trước trên các mô hình bản thân, nhưng điều đó sẽ không cần thiết trong phân tích này; các dao cạo Bayesian Occam của hóa ra là đủ để mã hóa một ưu tiên đối với các mô hình đơn giản hơn).
Thật không may, khả năng biên đúng, mà tích hợp trên cả các bang rời rạc \(z_{1:T}\) và (vector của) các thông số tốc độ \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) là không dễ xử lý cho mô hình này. Để thuận tiện, chúng tôi sẽ xấp xỉ nó sử dụng một cái gọi là " Bayes thực nghiệm " hoặc "gõ tối đa khả năng II" dự toán: thay vì hoàn toàn tích hợp các tham số (không rõ) tỷ lệ \(\lambda\) kết hợp với mỗi trạng thái hệ thống, chúng tôi sẽ tối ưu hóa trên các giá trị của chúng:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
Sự xấp xỉ này có thể quá phù hợp, tức là, nó sẽ thích các mô hình phức tạp hơn so với khả năng cận biên thực sự. Chúng ta có thể xem xét các phép xấp xỉ trung thực hơn, ví dụ như, tối ưu hóa một biến phân thấp hơn bị ràng buộc, hoặc sử dụng một Monte Carlo ước lượng như lấy mẫu quan trọng ủ ; chúng (đáng buồn là) nằm ngoài phạm vi của sổ tay này. (Để biết thêm về lựa chọn mô hình Bayes và xấp xỉ, chương 7 của tuyệt vời Machine Learning: một xác suất Perspective là một tài liệu tham khảo tốt.)
Về nguyên tắc, chúng ta có thể làm mô hình so sánh này chỉ đơn giản bằng việc tối ưu hóa chạy lại trên nhiều lần với các giá trị khác nhau của num_states , nhưng đó sẽ là rất nhiều công việc. Ở đây chúng ta sẽ thấy làm thế nào để xem xét nhiều mô hình song song, sử dụng TFP của batch_shape cơ chế vector hóa.
Ma trận chuyển tiếp và trạng thái ban đầu trước: thay vì xây dựng một mô tả mô hình duy nhất, bây giờ chúng ta sẽ xây dựng một loạt các ma trận chuyển đổi và logits trước, một cho mỗi mô hình ứng cử viên lên đến max_num_states . Để phân phối dễ dàng, chúng tôi sẽ cần đảm bảo rằng tất cả các phép tính có cùng một 'hình dạng': điều này phải tương ứng với kích thước của mô hình lớn nhất mà chúng tôi sẽ phù hợp. Để xử lý các mô hình nhỏ hơn, chúng tôi có thể 'nhúng' mô tả của chúng vào các kích thước trên cùng của không gian trạng thái, coi các kích thước còn lại là trạng thái giả không bao giờ được sử dụng một cách hiệu quả.
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
Bây giờ chúng ta tiến hành tương tự như trên. Lần này chúng tôi sẽ sử dụng một chiều kích hàng loạt bổ sung trong trainable_rates để phù hợp với riêng giá cho từng mô hình đang được xem xét.
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
Khi tính toán tổng xác suất nhật ký, chúng tôi cẩn thận chỉ tổng hợp các giá trị cơ bản cho các tỷ lệ thực sự được sử dụng bởi mỗi thành phần mô hình:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
Bây giờ chúng ta tối ưu hóa mục tiêu hàng loạt, chúng tôi đã xây dựng, phù hợp tất cả các mô hình ứng cử viên cùng một lúc:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
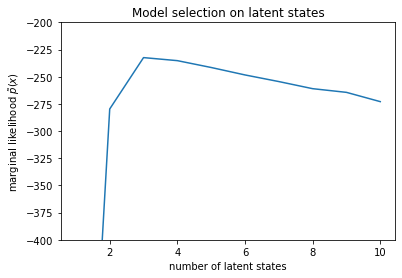
Kiểm tra khả năng xảy ra, chúng ta thấy rằng khả năng cận biên (gần đúng) có xu hướng thích mô hình ba trạng thái hơn. Điều này có vẻ khá hợp lý - mô hình 'đúng' có bốn trạng thái, nhưng chỉ nhìn vào dữ liệu, thật khó để loại trừ một lời giải thích ba trạng thái.
Chúng tôi cũng có thể trích xuất tỷ lệ phù hợp cho từng mô hình ứng viên:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
Và vẽ biểu đồ giải thích mà mỗi mô hình cung cấp cho dữ liệu:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
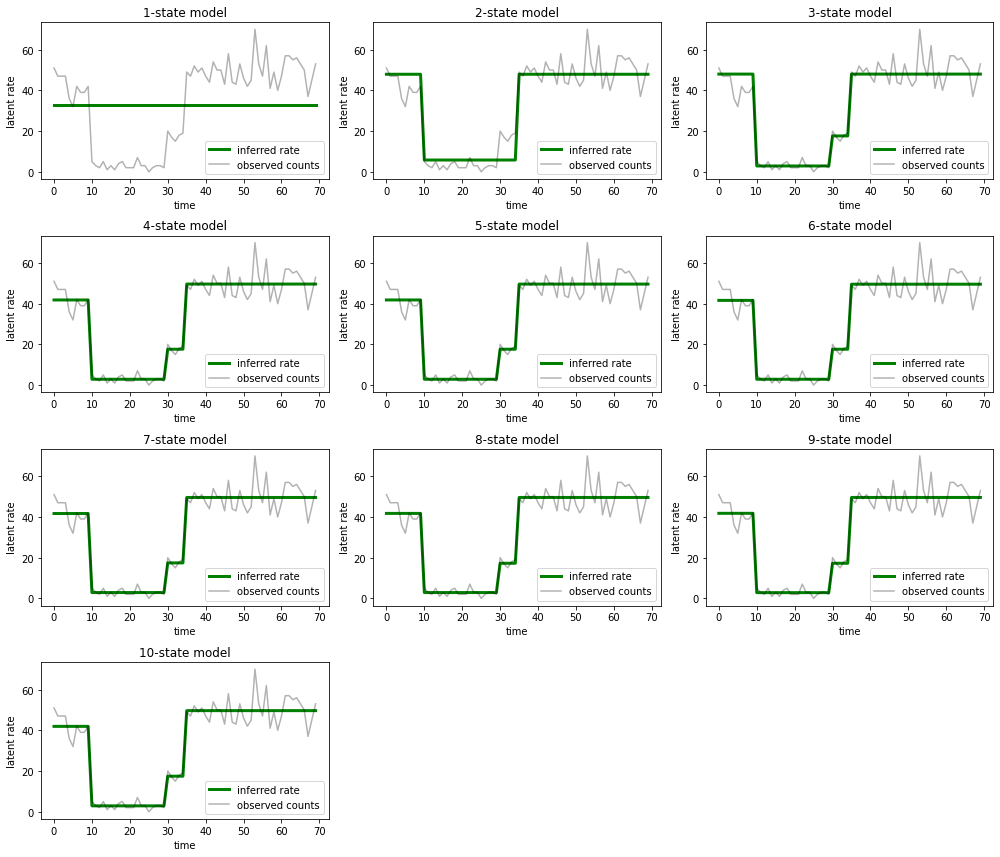
Thật dễ dàng để thấy cách các mô hình ba trạng thái một, hai và (tinh vi hơn) cung cấp những giải thích không đầy đủ. Thật thú vị, tất cả các mô hình ở trên bốn trạng thái đều cung cấp cùng một cách giải thích về cơ bản! Điều này có thể xảy ra bởi vì 'dữ liệu' của chúng tôi tương đối sạch và để lại ít chỗ cho các giải thích thay thế; trên dữ liệu thế giới thực lộn xộn hơn, chúng tôi mong đợi các mô hình dung lượng cao hơn sẽ cung cấp dần dần sự phù hợp tốt hơn với dữ liệu, với một số điểm cân bằng trong đó sự phù hợp được cải thiện bị đè nặng bởi độ phức tạp của mô hình.
Tiện ích mở rộng
Các mô hình trong máy tính xách tay này có thể được mở rộng một cách đơn giản theo nhiều cách. Ví dụ:
- cho phép các trạng thái tiềm ẩn có các xác suất khác nhau (một số trạng thái có thể phổ biến và hiếm gặp)
- cho phép chuyển đổi không đồng nhất giữa các trạng thái tiềm ẩn (ví dụ: để biết rằng sự cố máy thường được theo sau bởi khởi động lại hệ thống thường được theo sau bởi một khoảng thời gian hoạt động tốt, v.v.)
- mô hình phát thải khác, ví dụ như
NegativeBinomialđể mô hình phân tán trong dữ liệu số, hoặc phân phối liên tục thay đổi nhưNormalcho dữ liệu thực tế có giá trị.
