انتخاب مدل بیزی
 مشاهده در TensorFlow.org مشاهده در TensorFlow.org |  در Google Colab اجرا شود در Google Colab اجرا شود |  مشاهده منبع در GitHub مشاهده منبع در GitHub |  دانلود دفترچه یادداشت دانلود دفترچه یادداشت |
واردات
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
وظیفه: تشخیص نقطه تغییر با چندین نقطه تغییر
یک وظیفه تشخیص نقطه تغییر را در نظر بگیرید: رویدادها با سرعتی اتفاق میافتند که در طول زمان تغییر میکند، که ناشی از تغییرات ناگهانی در وضعیت (مشاهدهنشده) برخی از سیستمها یا فرآیندهایی است که دادهها را تولید میکند.
به عنوان مثال، ممکن است یک سری شمارش مانند زیر را مشاهده کنیم:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
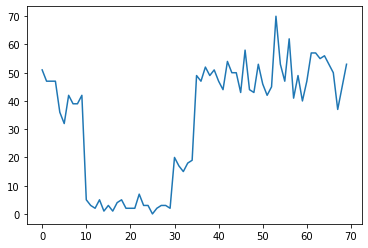
اینها میتوانند تعداد خرابیهای یک مرکز داده، تعداد بازدیدکنندگان یک صفحه وب، تعداد بستههای موجود در پیوند شبکه و غیره را نشان دهند.
توجه داشته باشید که تنها با مشاهده داده ها، به طور کامل مشخص نیست که چند رژیم سیستم متمایز وجود دارد. آیا می توانید بگویید هر یک از سه نقطه سوئیچ کجا رخ می دهد؟
تعداد مشخص ایالت
ابتدا موردی (شاید غیر واقعی) را در نظر می گیریم که در آن تعداد حالت های مشاهده نشده از قبل مشخص است. در اینجا، فرض می کنیم می دانیم که چهار حالت نهفته وجود دارد.
ما این مشکل را به عنوان یک مدل (ناهمگن) فرایند پواسون تعویض: در هر نقطه از زمان، تعدادی از رویدادهایی که رخ می دهد است پواسون توزیع، و نرخ حوادث توسط مشاهده نشده سیستم دولتی تعیین \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
کشورهای نهفته گسسته عبارتند از: \(z_t \in \{1, 2, 3, 4\}\)، بنابراین \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) یک بردار ساده حاوی نرخ پواسون برای هر ایالت است. به مدل تکامل ایالات در طول زمان، ما یک مدل انتقال ساده و تعریف \(p(z_t | z_{t-1})\): اجازه دهید بگویم که در هر مرحله در حالت قبلی با احتمال ماندن \(p\)، و با احتمال \(1-p\) گذار ما به یک حالت های مختلف به طور یکنواخت به صورت تصادفی حالت اولیه نیز به صورت تصادفی یکنواخت انتخاب می شود، بنابراین داریم:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
این فرضیات به یک مطابقت مدل پنهان مارکوف با انتشار پواسون است. ما می توانیم آنها را در بهره وری کل عوامل با استفاده از رمز tfd.HiddenMarkovModel . ابتدا ماتریس انتقال و یکنواخت قبل را در حالت اولیه تعریف می کنیم:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
بعد، ما ساخت یک tfd.HiddenMarkovModel توزیع، استفاده از یک متغیر تربیت شدنی برای نشان دادن نرخ مربوط به هر حالت سیستم. ما نرخ ها را در log-space پارامتر می کنیم تا مطمئن شویم که ارزش مثبت دارند.
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
در نهایت، چگالی ورود به سیستم کل مدل را تعریف می کنیم، از جمله لگ نرمال ضعیف-آموزنده قبل در نرخ، و اجرای بهینه ساز برای محاسبه حداکثر پسینی (MAP) برازش داده شده تعداد مشاهده.
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
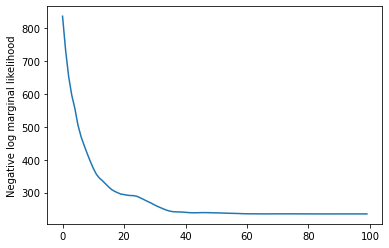
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
کار کرد! توجه داشته باشید که حالتهای نهفته در این مدل فقط تا جایگشت قابل شناسایی هستند، بنابراین نرخهایی که ما بازیابی کردیم به ترتیب متفاوتی هستند و کمی نویز وجود دارد، اما به طور کلی به خوبی مطابقت دارند.
بازیابی مسیر وضعیت
حالا که ما این جا مدل، ما ممکن است بخواهید برای بازسازی که دولت مدل معتقد است که سیستم در در هر timestep بود.
این یک وظیفه استنتاج خلفی است: با توجه به تعداد مشاهده \(x_{1:T}\) و پارامترهای مدل (نرخ) \(\lambda\)، ما می خواهیم برای پی بردن به دنباله ای از متغیرهای پنهان گسسته، پس از توزیع خلفی \(p(z_{1:T} | x_{1:T}, \lambda)\). در یک مدل پنهان مارکوف، ما میتوانیم حاشیهها و سایر ویژگیهای این توزیع را با استفاده از الگوریتمهای استاندارد ارسال پیام محاسبه کنیم. به طور خاص، posterior_marginals روش موثر محاسبه خواهد شد (با استفاده از الگوریتم رو به جلو به عقب ) حاشیه توزیع احتمال \(p(Z_t = z_t | x_{1:T})\) بیش از گسسته نهفته دولت \(Z_t\) در هر timestep \(t\).
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
با ترسیم احتمالات پسین، "توضیحات" مدل از داده ها را بازیابی می کنیم: هر حالت در کدام نقطه از زمان فعال است؟
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
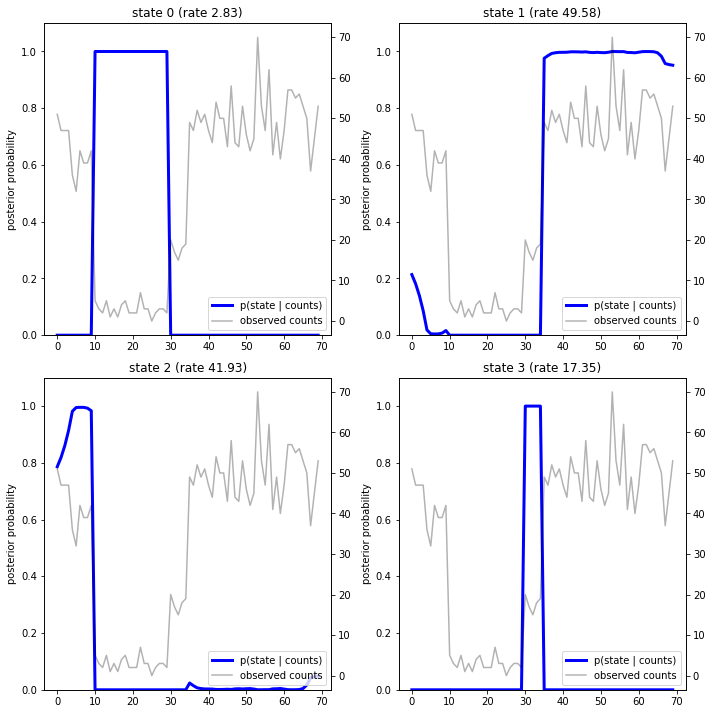
در این مورد (ساده)، میبینیم که مدل معمولاً کاملاً مطمئن است: در اکثر مراحل زمانی اساساً تمام جرم احتمال را به یکی از چهار حالت اختصاص میدهد. خوشبختانه، توضیحات منطقی به نظر می رسند!
ما همچنین می توانیم این خلفی تجسم از نظر نرخ مرتبط با ترین حالت نهفته به احتمال زیاد در هر timestep، تغلیظ خلفی احتمالاتی به یک توضیح تک:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
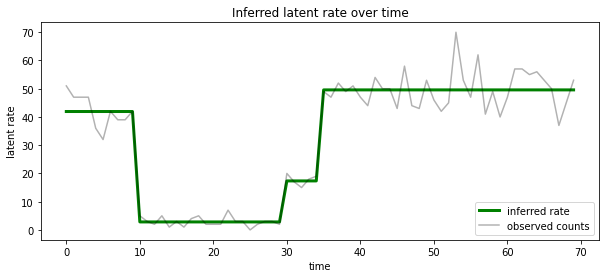
تعداد نامشخص ایالت
در مشکلات واقعی، ممکن است تعداد «واقعی» حالتهای سیستمی را که مدلسازی میکنیم ندانیم. این ممکن است همیشه نگرانکننده نباشد: اگر به هویت حالتهای ناشناخته اهمیتی نمیدهید، میتوانید مدلی را با حالتهای بیشتر از آنچه مدل نیاز دارد اجرا کنید و (چیزی شبیه) یک دسته از موارد تکراری را یاد بگیرید. کپی از حالات واقعی اما بیایید فرض کنیم که شما به استنباط تعداد «واقعی» حالتهای نهفته اهمیت میدهید.
ما می توانیم این را به عنوان یک مورد از مشاهده انتخاب مدل بیزی : ما یک مجموعه ای از مدل نامزد، هر کدام با شماره های مختلف از کشورهای نهفته است، و ما می خواهیم به انتخاب یکی از این است که به احتمال زیاد داده های مشاهده شده به تولید کرده اند. برای انجام این کار، ما احتمال حاشیه ای از داده ها محاسبه تحت هر مدل (ما همچنین می تواند قبل در مدل های خود اضافه کنید، اما که نمی خواهد در این تجزیه و تحلیل لازم باشد؛ تیغ بیزی اوکام معلوم می شود به رمز کافی ترجیح نسبت به مدل های ساده تر).
متاسفانه، احتمال حاشیه ای درست، که ادغام بیش از هر دو حالت مجزا \(z_{1:T}\) و (بردار) پارامترهای نرخ \(\lambda\)، \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) است رام برای این مدل است. برای راحتی، ما آن را تقریب با استفاده از یک به اصطلاح " بیز تجربی " یا "نوع II حداکثر احتمال" برآورد: به جای به طور کامل یکپارچه سازی از پارامترهای (ناشناخته) نرخ \(\lambda\) مرتبط با هر حالت سیستم، ما بهینه سازی بیش از ارزش های آنها:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
این تقریب ممکن است بیش از حد مناسب باشد، به عنوان مثال، مدل های پیچیده تری را نسبت به احتمال نهایی واقعی ترجیح می دهد. ما می توانیم تقریب وفادار تر، به عنوان مثال در نظر بگیرید، بهینه سازی یک متغیر کران پایین، و یا با استفاده از یک مونت کارلو برآوردگر مانند نمونه برداری اهمیت آنیل ؛ اینها (متاسفانه) فراتر از محدوده این دفترچه هستند. (برای اطلاعات بیشتر در انتخاب مدل بیزی و تقریب، فصل 7 از عالی یادگیری ماشین: یک احتمالاتی چشم انداز یک مرجع خوب است.)
در اصل، ما می تواند این مقایسه مدل به سادگی با اجرای دوباره بهینه سازی بالا چند بار با مقادیر مختلف انجام num_states ، اما این امر می تواند بسیار کار می کنند. در اینجا، ما نشان دهد که چگونه به در نظر گرفتن مدل های متعدد به صورت موازی، با استفاده از بهره وری کل عوامل را batch_shape مکانیسم برای vectorization.
ماتریس انتقال و حالت اولیه قبل: به جای ساختمان شرح مدل واحد، در حال حاضر ما یک دسته ای از ماتریس انتقال و logits قبل، یکی برای هر مدل نامزد برای ساخت max_num_states . برای دستهبندی آسان، باید اطمینان حاصل کنیم که همه محاسبات «شکل» یکسانی دارند: این باید با ابعاد بزرگترین مدلی مطابقت داشته باشد. برای رسیدگی به مدلهای کوچکتر، میتوانیم توصیفهای آنها را در بالاترین ابعاد فضای حالت «جاسازی» کنیم، و به طور مؤثر ابعاد باقیمانده را بهعنوان حالتهای ساختگی در نظر بگیریم که هرگز استفاده نمیشوند.
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
حالا مانند بالا عمل می کنیم. این بار ما یک بعد دسته ای اضافی در استفاده trainable_rates به طور جداگانه متناسب با نرخ برای هر مدل مورد نظر.
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
در محاسبه کل log prob، ما مراقب هستیم که فقط پیشینها را برای نرخهای واقعی استفاده شده توسط هر جزء مدل جمع کنیم:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
در حال حاضر ما بهینه سازی هدف دسته ای ما ساخته ایم، اتصالات تمام مدل های نامزد به طور همزمان:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
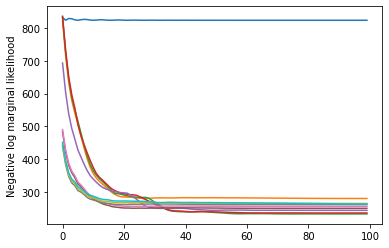
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
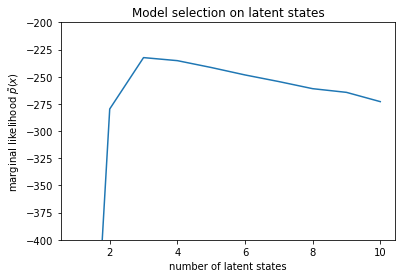
با بررسی احتمالات، می بینیم که احتمال نهایی (تقریبی) تمایل به ترجیح مدل سه حالته دارد. این کاملاً محتمل به نظر می رسد - مدل "واقعی" چهار حالت داشت، اما با نگاه کردن به داده ها، رد توضیح سه حالته دشوار است.
همچنین میتوانیم نرخهای مناسب برای هر مدل کاندید را استخراج کنیم:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
و توضیحاتی را که هر مدل برای داده ها ارائه می دهد رسم کنید:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
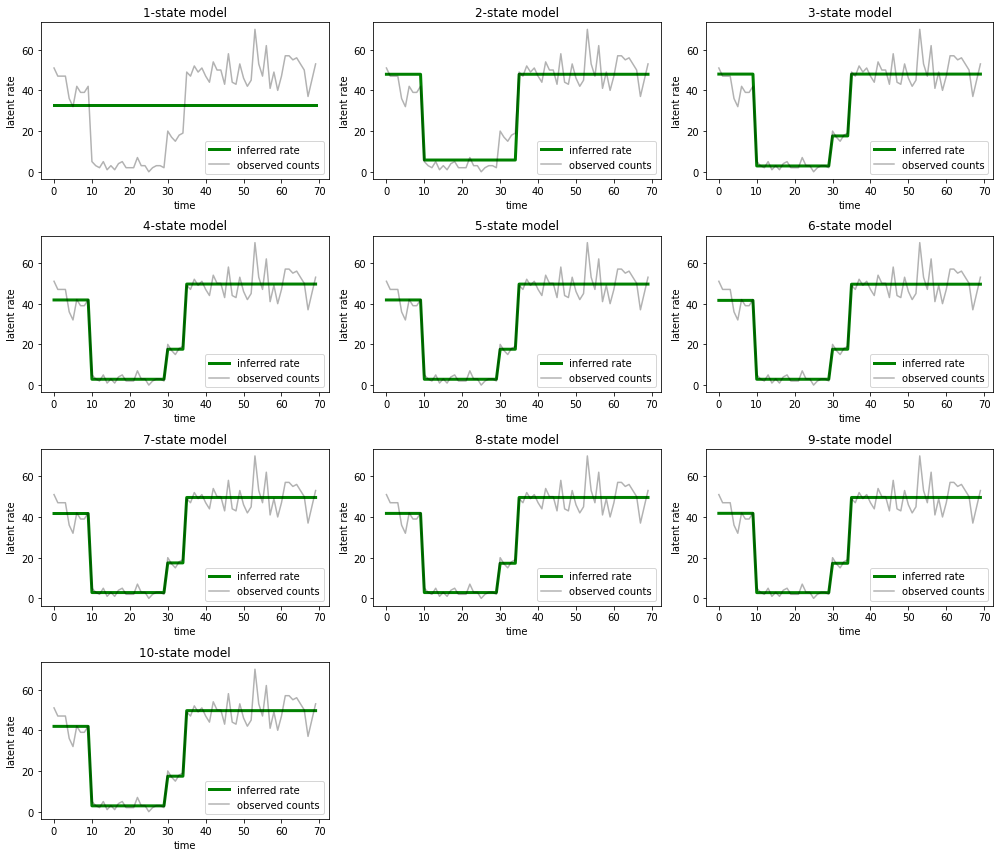
به راحتی می توان دید که چگونه مدل های یک، دو، و (به طور ظریف تر) سه حالته توضیحات ناکافی ارائه می دهند. جالب اینجاست که همه مدل های بالای چهار حالت اساساً توضیح مشابهی ارائه می دهند! این احتمالاً به این دلیل است که «دادههای» ما نسبتاً تمیز هستند و فضای کمی برای توضیحات جایگزین باقی میگذارند. در دادههای دنیای واقعی به هم ریختهتر، ما انتظار داریم که مدلهای با ظرفیت بالاتر به تدریج تناسب بهتری با دادهها ارائه کنند، با برخی از نقاط معاوضه که در آن تناسب بهبود یافته با پیچیدگی مدل بیشتر است.
برنامه های افزودنی
مدلهای این نوتبوک را میتوان به روشهای مختلف بهراحتی گسترش داد. مثلا:
- اجازه دادن به حالت های نهفته برای داشتن احتمالات مختلف (برخی حالت ها ممکن است رایج در مقابل نادر باشند)
- اجازه دادن به انتقال غیریکنواخت بین حالتهای نهفته (مثلاً یاد گرفتن اینکه خرابی ماشین معمولاً با راهاندازی مجدد سیستم همراه است و معمولاً با یک دوره عملکرد خوب و غیره)
- سایر مدل ها انتشار، به عنوان مثال
NegativeBinomialبه مدل پراکندگی در داده های شمارش، و یا توزیع مستمر مختلف مانندNormalبرای داده های حقیقی.
