Selezione del modello bayesiano
 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza la fonte su GitHub Visualizza la fonte su GitHub |  Scarica taccuino Scarica taccuino |
Importazioni
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
Compito: rilevamento changepoint con più changepoint
Considera un'attività di rilevamento del punto di modifica: gli eventi accadono a una velocità che cambia nel tempo, guidata da cambiamenti improvvisi nello stato (non osservato) di alcuni sistemi o processi che generano i dati.
Ad esempio, potremmo osservare una serie di conteggi come il seguente:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
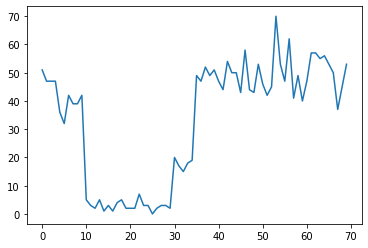
Questi potrebbero rappresentare il numero di guasti in un datacenter, il numero di visitatori di una pagina Web, il numero di pacchetti su un collegamento di rete, ecc.
Nota che non è del tutto evidente quanti regimi di sistema distinti ci siano solo guardando i dati. Puoi dire dove si verifica ciascuno dei tre punti di commutazione?
Numero noto di stati
Consideriamo prima il caso (forse irrealistico) in cui il numero di stati non osservati è noto a priori. Qui, supponiamo di sapere che ci sono quattro stati latenti.
Modelliamo questo problema come una commutazione (disomogeneo) processo di Poisson: in ogni punto nel tempo, il numero di eventi che si verificano sia Poisson, e il tasso di eventi è determinato dal inosservato stato del sistema \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
Gli stati latenti sono discrete: \(z_t \in \{1, 2, 3, 4\}\), così \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) è un vettore semplice contenente un tasso di Poisson per ciascuno stato. Per modellare l'evoluzione degli stati nel corso del tempo, ci definiamo un semplice modello di transizione \(p(z_t | z_{t-1})\): Diciamo che ad ogni passo restiamo nello stato precedente, con una certa probabilità \(p\), e con probabilità \(1-p\) abbiamo transizione verso un stato diverso uniformemente a caso. Anche lo stato iniziale è scelto uniformemente a caso, quindi abbiamo:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
Queste ipotesi corrispondono a un modello di Markov nascosto con emissioni di Poisson. Possiamo codificare in TFP utilizzando tfd.HiddenMarkovModel . Innanzitutto, definiamo la matrice di transizione e l'uniforme a priori sullo stato iniziale:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
Successivamente, abbiamo costruire un tfd.HiddenMarkovModel distribuzione, utilizzando una variabile addestrabile per rappresentare le tariffe associate a ciascun stato del sistema. Parametrizziamo le tariffe in log-space per assicurarci che siano valutate positivamente.
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
Infine, definiamo la densità totale di registro del modello, tra cui un Lognormale debolmente informativa preventiva sulle tariffe, ed eseguire un ottimizzatore per calcolare la massima a posteriori fit (MAP) ai dati di conteggio osservata.
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
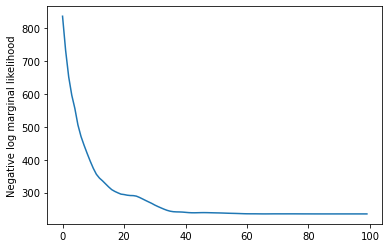
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
Ha funzionato! Nota che gli stati latenti in questo modello sono identificabili solo fino alla permutazione, quindi i tassi che abbiamo recuperato sono in un ordine diverso e c'è un po' di rumore, ma generalmente corrispondono abbastanza bene.
Recuperare la traiettoria dello stato
Ora che abbiamo adattare il modello, potremmo volere di ricostruire quale stato il modello ritiene che il sistema era in ad ogni passo temporale.
Questo è un compito inferenza posteriori: visti i conteggi osservati \(x_{1:T}\) e parametri del modello (tassi) \(\lambda\), vogliamo dedurre la sequenza delle variabili latenti discrete, a seguito della distribuzione posteriori \(p(z_{1:T} | x_{1:T}, \lambda)\). In un modello di Markov nascosto, possiamo calcolare in modo efficiente i marginali e altre proprietà di questa distribuzione utilizzando algoritmi standard di passaggio dei messaggi. In particolare, il posterior_marginals metodo efficiente calcolare (usando l' algoritmo avanti-indietro ) la distribuzione di probabilità marginale \(p(Z_t = z_t | x_{1:T})\) sul discreti latente stato \(Z_t\) ad ogni passo temporale \(t\).
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
Tracciando le probabilità a posteriori, recuperiamo la "spiegazione" dei dati del modello: in quali momenti è attivo ogni stato?
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
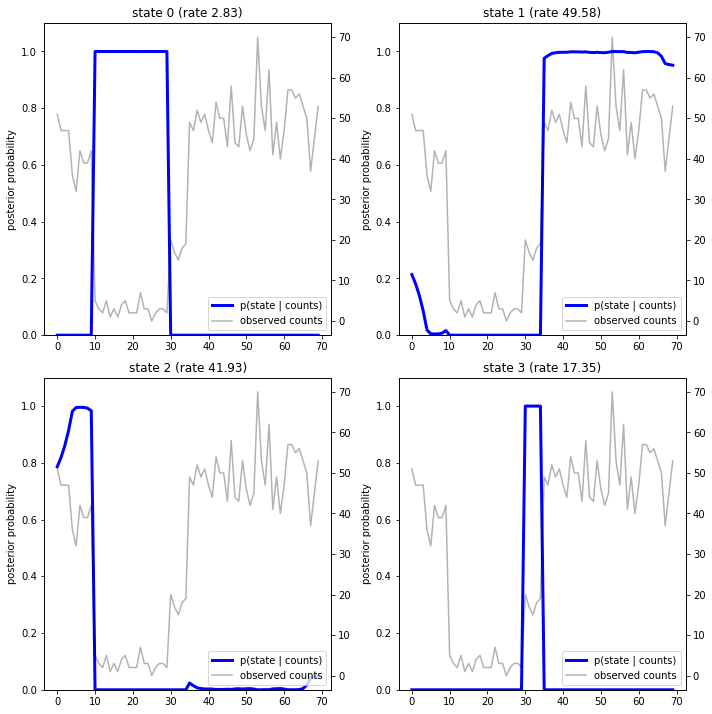
In questo (semplice) caso, vediamo che il modello di solito è abbastanza sicuro: nella maggior parte dei tempi assegna essenzialmente tutte le probabilità di massa a uno solo dei quattro stati. Fortunatamente, le spiegazioni sembrano ragionevoli!
Possiamo anche visualizzare questa posteriori in termini di tasso associato con il più probabile stato latente ad ogni passo temporale, condensazione posteriore probabilistico in un'unica spiegazione:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
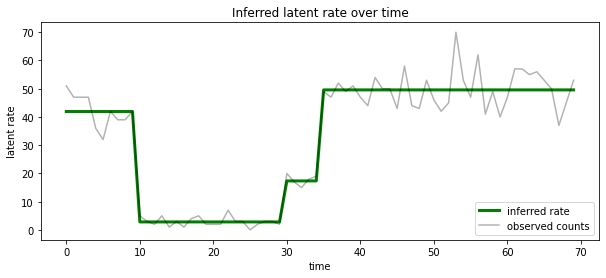
Numero sconosciuto di stati
Nei problemi reali, potremmo non conoscere il "vero" numero di stati nel sistema che stiamo modellando. Questo potrebbe non essere sempre un problema: se non ti interessano particolarmente le identità degli stati sconosciuti, potresti semplicemente eseguire un modello con più stati di quanti ne conosci e imparare (qualcosa come) un mucchio di duplicati copie degli stati reali. Ma supponiamo che ti interessi dedurre il "vero" numero di stati latenti.
Possiamo vedere questo come un caso di selezione del modello bayesiano : abbiamo una serie di modelli candidati, ognuno con un diverso numero di stati latenti, e vogliamo scegliere quello che è più probabile che abbia generato i dati osservati. Per fare questo, calcoliamo la probabilità marginali dei dati in ciascun modello (potremmo anche aggiungere una preventiva sui modelli stessi, ma che non sarà necessario in questa analisi, il rasoio di Bayesiano Occam risulta essere sufficiente per codificare un preferenza verso modelli più semplici).
Purtroppo, la vera probabilità marginali, che integra oltre entrambi gli stati discreti \(z_{1:T}\) e la (vettore di parametri) a tasso \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) non è trattabile per questo modello. Per comodità, ci approssimare utilizzando un cosiddetto " Bayes empirici " o "di tipo II massima verosimiglianza" stima: invece di piena integrazione i parametri (sconosciuto) tasso \(\lambda\) associato ad ogni stato del sistema, noi ottimizziamo sui loro valori:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
Questa approssimazione potrebbe sovraadattarsi, cioè preferirà modelli più complessi rispetto alla vera verosimiglianza marginale. Potremmo considerare approssimazioni più fedeli, per esempio, l'ottimizzazione di un variazionali limite inferiore, o usando un Monte Carlo stimatore come ad esempio il campionamento importanza ricotto ; questi sono (purtroppo) oltre lo scopo di questo notebook. (Per maggiori informazioni sulla selezione del modello bayesiano e approssimazioni, il capitolo 7 della eccellente Machine Learning: una prospettiva probabilistica è un riferimento buono.)
In linea di principio, potremmo fare questo confronto modello semplicemente eseguendo nuovamente l'ottimizzazione sopra molte volte con valori diversi di num_states , ma che sarebbe un sacco di lavoro. Qui vi mostreremo come considerare più modelli in parallelo, utilizzando di TFP batch_shape meccanismo per la vettorializzazione.
Matrice di transizione e lo stato iniziale prima: piuttosto che costruire un singolo modello di descrizione, ora faremo costruire una serie di matrici di transizione e logit precedenti, uno per ogni modello candidato fino a max_num_states . Per semplificare il batch dovremo assicurarci che tutti i calcoli abbiano la stessa "forma": questa deve corrispondere alle dimensioni del modello più grande che andremo a montare. Per gestire modelli più piccoli, possiamo "incorporare" le loro descrizioni nelle dimensioni più alte dello spazio degli stati, trattando efficacemente le dimensioni rimanenti come stati fittizi che non vengono mai utilizzati.
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
Ora procediamo come sopra. Questa volta useremo una dimensione extra batch trainable_rates per adattarsi a parte le tariffe per ciascun modello in esame.
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
Nel calcolare il log prob totale, facciamo attenzione a sommare solo i priori per i tassi effettivamente utilizzati da ciascun componente del modello:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
Ora ottimizziamo l'obiettivo lotto abbiamo costruito, inserendo tutti i modelli candidati contemporaneamente:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
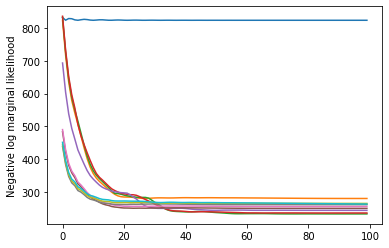
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
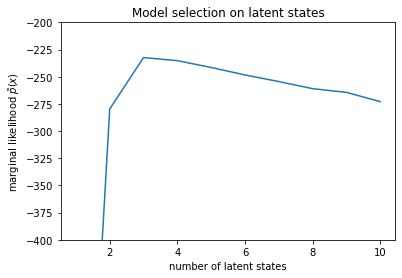
Esaminando le verosimiglianze, vediamo che la verosimiglianza marginale (approssimativa) tende a preferire un modello a tre stati. Questo sembra abbastanza plausibile: il modello "vero" aveva quattro stati, ma semplicemente guardando i dati è difficile escludere una spiegazione a tre stati.
Possiamo anche estrarre le tariffe adatte a ciascun modello candidato:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
E traccia le spiegazioni fornite da ciascun modello per i dati:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
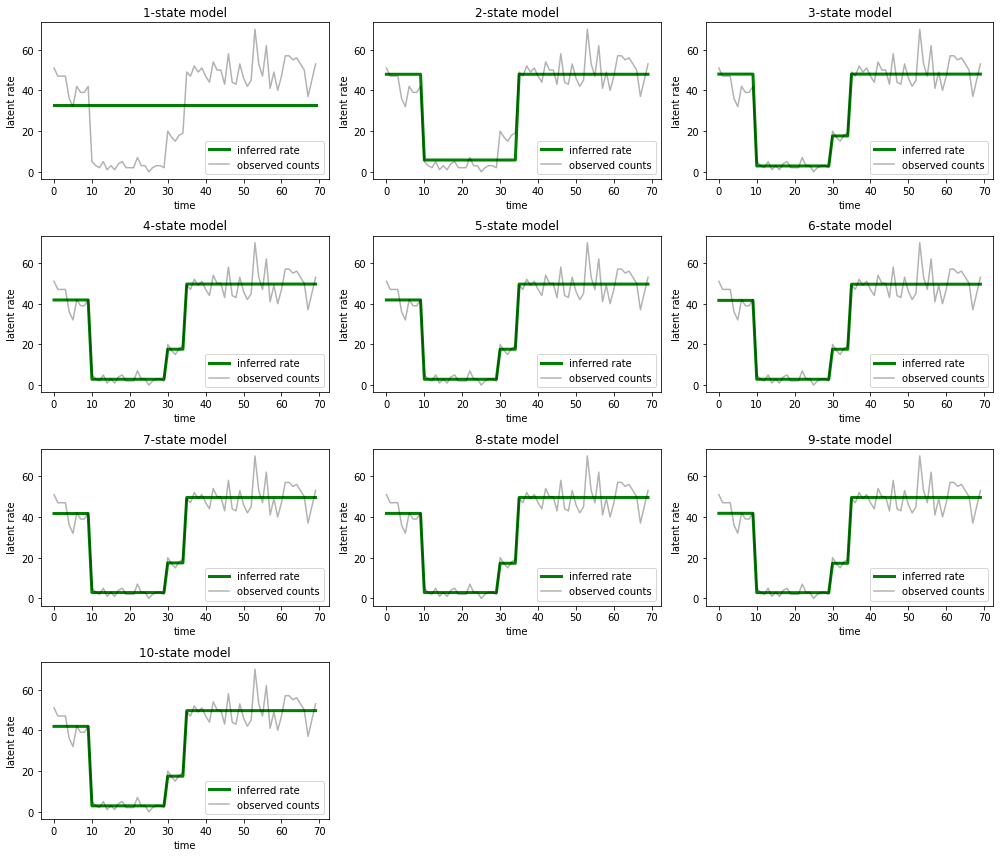
È facile vedere come i modelli a uno, due e (più sottilmente) tre stati forniscano spiegazioni inadeguate. È interessante notare che tutti i modelli al di sopra dei quattro stati forniscono essenzialmente la stessa spiegazione! Ciò è probabilmente dovuto al fatto che i nostri "dati" sono relativamente puliti e lasciano poco spazio a spiegazioni alternative; su dati del mondo reale più disordinati ci aspetteremmo che i modelli con capacità più elevate forniscano adattamenti progressivamente migliori ai dati, con un punto di compromesso in cui l'adattamento migliorato è superato dalla complessità del modello.
estensioni
I modelli di questo notebook possono essere facilmente estesi in molti modi. Per esempio:
- consentire agli stati latenti di avere probabilità diverse (alcuni stati possono essere comuni o rari)
- consentire transizioni non uniformi tra stati latenti (ad esempio, apprendere che un arresto anomalo della macchina è solitamente seguito da un riavvio del sistema è solitamente seguito da un periodo di buone prestazioni, ecc.)
- altri modelli di emissione, ad esempio
NegativeBinomialdi modellare dispersioni in dati di conteggio, o distribuzioni continue variabile comeNormalper i dati a valori reali.
