 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看 |
 在 Google Colab 中运行 在 Google Colab 中运行 |
 在 GitHub 上查看源代码 在 GitHub 上查看源代码 |
 下载笔记本 下载笔记本 |
本教程通过以下三个示例介绍自编码器:基础知识、图像降噪和异常检测。
自编码器是一种特殊类型的神经网络,经过训练后可将其输入复制到其输出。例如,给定一个手写数字的图像,自编码器首先将图像编码为低维的潜在表示,然后将该潜在表示解码回图像。自编码器学习压缩数据,同时最大程度地减少重构误差。
要详细了解自编码器,请考虑阅读 Ian Goodfellow、Yoshua Bengio 和 Aaron Courville 撰写的《深度学习》一书的第 14 章。
导入 TensorFlow 和其他库
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.model_selection import train_test_split
from tensorflow.keras import layers, losses
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Model
2023-11-07 19:41:16.708459: E external/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:9261] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2023-11-07 19:41:16.708505: E external/local_xla/xla/stream_executor/cuda/cuda_fft.cc:607] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2023-11-07 19:41:16.710018: E external/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1515] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered
加载数据集
首先,您将使用 Fashion MNIST 数据集训练基本自编码器。此数据集中的每个图像均为 28x28 像素。
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
print (x_train.shape)
print (x_test.shape)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz 29515/29515 [==============================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz 26421880/26421880 [==============================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz 5148/5148 [==============================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz 4422102/4422102 [==============================] - 0s 0us/step (60000, 28, 28) (10000, 28, 28)
第一个示例:基本自编码器

定义一个具有两个密集层的自编码器:一个将图像压缩为 64 维隐向量的 encoder,以及一个从隐空间重构原始图像的 decoder。
要定义模型,请使用 Keras Model Subclassing API。
latent_dim = 64
class Autoencoder(Model):
def __init__(self, latent_dim):
super(Autoencoder, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential([
layers.Flatten(),
layers.Dense(latent_dim, activation='relu'),
])
self.decoder = tf.keras.Sequential([
layers.Dense(784, activation='sigmoid'),
layers.Reshape((28, 28))
])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Autoencoder(latent_dim)
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
使用 x_train 作为输入和目标来训练模型。encoder 会学习将数据集从 784 个维度压缩到隐空间,而 decoder 将学习重构原始图像。
autoencoder.fit(x_train, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test, x_test))
Epoch 1/10 WARNING: All log messages before absl::InitializeLog() is called are written to STDERR I0000 00:00:1699386084.268834 448569 device_compiler.h:186] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process. 1875/1875 [==============================] - 6s 2ms/step - loss: 0.0238 - val_loss: 0.0132 Epoch 2/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0117 - val_loss: 0.0108 Epoch 3/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0102 - val_loss: 0.0098 Epoch 4/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0095 - val_loss: 0.0094 Epoch 5/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0092 - val_loss: 0.0092 Epoch 6/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0091 - val_loss: 0.0091 Epoch 7/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0090 - val_loss: 0.0090 Epoch 8/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0089 - val_loss: 0.0090 Epoch 9/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0088 - val_loss: 0.0089 Epoch 10/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0088 - val_loss: 0.0089 <keras.src.callbacks.History at 0x7ff7fd32d7c0>
现在,模型已经训练完成,我们通过对测试集中的图像进行编码和解码来测试该模型。
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original
ax = plt.subplot(2, n, i + 1)
plt.imshow(x_test[i])
plt.title("original")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
ax = plt.subplot(2, n, i + 1 + n)
plt.imshow(decoded_imgs[i])
plt.title("reconstructed")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

第二个示例:图像降噪

经过训练后,自编码器还可以去除图像中的噪点。在以下部分中,您将通过对每个图像应用随机噪声来创建有噪版本的 Fashion MNIST 数据集。随后,您将使用有噪图像作为输入并以原始图像作为目标来训练自编码器。
我们重新导入数据集以忽略之前所做的修改:
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train[..., tf.newaxis]
x_test = x_test[..., tf.newaxis]
print(x_train.shape)
(60000, 28, 28, 1)
向图像添加随机噪声:
noise_factor = 0.2
x_train_noisy = x_train + noise_factor * tf.random.normal(shape=x_train.shape)
x_test_noisy = x_test + noise_factor * tf.random.normal(shape=x_test.shape)
x_train_noisy = tf.clip_by_value(x_train_noisy, clip_value_min=0., clip_value_max=1.)
x_test_noisy = tf.clip_by_value(x_test_noisy, clip_value_min=0., clip_value_max=1.)
绘制有噪图像:
n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
plt.show()

定义卷积自编码器
在此示例中,您将使用 encoder 中的 Conv2D 层和 decoder 中的 Conv2DTranspose 层来训练卷积自编码器。
class Denoise(Model):
def __init__(self):
super(Denoise, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Input(shape=(28, 28, 1)),
layers.Conv2D(16, (3, 3), activation='relu', padding='same', strides=2),
layers.Conv2D(8, (3, 3), activation='relu', padding='same', strides=2)])
self.decoder = tf.keras.Sequential([
layers.Conv2DTranspose(8, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2DTranspose(16, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2D(1, kernel_size=(3, 3), activation='sigmoid', padding='same')])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Denoise()
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
autoencoder.fit(x_train_noisy, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test_noisy, x_test))
Epoch 1/10 1875/1875 [==============================] - 10s 4ms/step - loss: 0.0162 - val_loss: 0.0093 Epoch 2/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0086 - val_loss: 0.0081 Epoch 3/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0076 - val_loss: 0.0073 Epoch 4/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0072 - val_loss: 0.0071 Epoch 5/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0070 - val_loss: 0.0070 Epoch 6/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0069 - val_loss: 0.0069 Epoch 7/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0068 - val_loss: 0.0068 Epoch 8/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0068 - val_loss: 0.0068 Epoch 9/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0067 - val_loss: 0.0067 Epoch 10/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0067 - val_loss: 0.0067 <keras.src.callbacks.History at 0x7ff82e75c910>
我们来看一下编码器的摘要。请注意图像是如何从 28x28 像素下采样为 7x7 像素的。
autoencoder.encoder.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 14, 14, 16) 160
conv2d_1 (Conv2D) (None, 7, 7, 8) 1160
=================================================================
Total params: 1320 (5.16 KB)
Trainable params: 1320 (5.16 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________
解码器将图像从 7x7 像素上采样为 28x28 像素。
autoencoder.decoder.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_transpose (Conv2DTr (None, 14, 14, 8) 584
anspose)
conv2d_transpose_1 (Conv2D (None, 28, 28, 16) 1168
Transpose)
conv2d_2 (Conv2D) (None, 28, 28, 1) 145
=================================================================
Total params: 1897 (7.41 KB)
Trainable params: 1897 (7.41 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________
绘制由自编码器生成的有噪图像和去噪图像。
encoded_imgs = autoencoder.encoder(x_test_noisy).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original + noise
ax = plt.subplot(2, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
bx = plt.subplot(2, n, i + n + 1)
plt.title("reconstructed")
plt.imshow(tf.squeeze(decoded_imgs[i]))
plt.gray()
bx.get_xaxis().set_visible(False)
bx.get_yaxis().set_visible(False)
plt.show()

第三个示例:异常检测
概述
在此示例中,您将训练自编码器来检测 ECG5000 数据集上的异常。此数据集包含 5,000 个心电图,每个心电图拥有 140 个数据点。您将使用简化版的数据集,其中每个样本都被标记为 0(对应于异常心律)或 1(对应于正常心律)。您需要关注如何识别异常心律。
注:这是一个有标签的数据集,因此您可以将其表述为一个监督学习问题。此示例的目标是说明可应用于没有可用标签的大型数据集的异常检测概念(例如,如果您有成千上万个正常心律,而只有少量异常心律)。
您将如何使用自编码器检测异常?回想一下,自编码器经过训练后可最大程度地减少重构误差。您将只基于正常心律训练自编码器,随后使用它来重构所有数据。我们的假设是,异常心律存在更高的重构误差。随后,如果重构误差超过固定阈值,则将心律分类为异常。
加载心电图数据
您将使用的数据集基于 timeseriesclassification.com 中的数据集。
# Download the dataset
dataframe = pd.read_csv('http://storage.googleapis.com/download.tensorflow.org/data/ecg.csv', header=None)
raw_data = dataframe.values
dataframe.head()
# The last element contains the labels
labels = raw_data[:, -1]
# The other data points are the electrocadriogram data
data = raw_data[:, 0:-1]
train_data, test_data, train_labels, test_labels = train_test_split(
data, labels, test_size=0.2, random_state=21
)
将数据归一化为 [0,1]。
min_val = tf.reduce_min(train_data)
max_val = tf.reduce_max(train_data)
train_data = (train_data - min_val) / (max_val - min_val)
test_data = (test_data - min_val) / (max_val - min_val)
train_data = tf.cast(train_data, tf.float32)
test_data = tf.cast(test_data, tf.float32)
您将仅使用正常心律训练自编码器,在此数据集中,正常心律被标记为 1。将正常心律与异常心律分开。
train_labels = train_labels.astype(bool)
test_labels = test_labels.astype(bool)
normal_train_data = train_data[train_labels]
normal_test_data = test_data[test_labels]
anomalous_train_data = train_data[~train_labels]
anomalous_test_data = test_data[~test_labels]
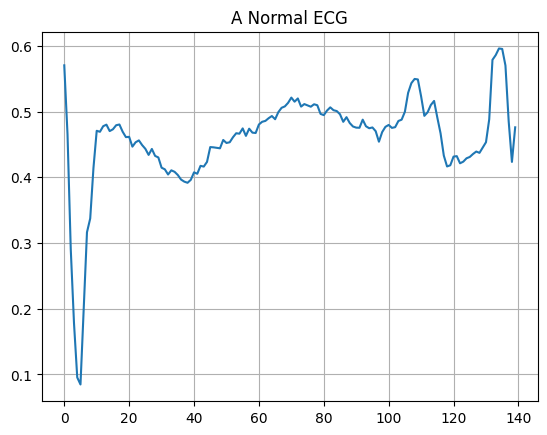
绘制正常的心电图。
plt.grid()
plt.plot(np.arange(140), normal_train_data[0])
plt.title("A Normal ECG")
plt.show()
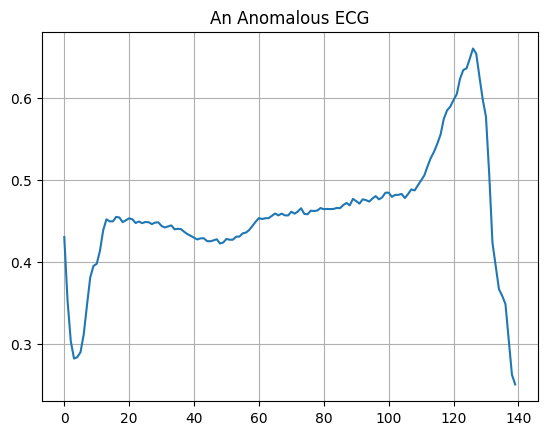
绘制异常的心电图。
plt.grid()
plt.plot(np.arange(140), anomalous_train_data[0])
plt.title("An Anomalous ECG")
plt.show()
构建模型
class AnomalyDetector(Model):
def __init__(self):
super(AnomalyDetector, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Dense(32, activation="relu"),
layers.Dense(16, activation="relu"),
layers.Dense(8, activation="relu")])
self.decoder = tf.keras.Sequential([
layers.Dense(16, activation="relu"),
layers.Dense(32, activation="relu"),
layers.Dense(140, activation="sigmoid")])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = AnomalyDetector()
autoencoder.compile(optimizer='adam', loss='mae')
请注意,自编码器仅使用正常的心电图进行训练,但使用完整的测试集进行评估。
history = autoencoder.fit(normal_train_data, normal_train_data,
epochs=20,
batch_size=512,
validation_data=(test_data, test_data),
shuffle=True)
Epoch 1/20 5/5 [==============================] - 2s 47ms/step - loss: 0.0575 - val_loss: 0.0530 Epoch 2/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0548 - val_loss: 0.0510 Epoch 3/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0509 - val_loss: 0.0492 Epoch 4/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0464 - val_loss: 0.0469 Epoch 5/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0416 - val_loss: 0.0444 Epoch 6/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0373 - val_loss: 0.0420 Epoch 7/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0337 - val_loss: 0.0406 Epoch 8/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0310 - val_loss: 0.0396 Epoch 9/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0291 - val_loss: 0.0389 Epoch 10/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0277 - val_loss: 0.0381 Epoch 11/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0265 - val_loss: 0.0373 Epoch 12/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0255 - val_loss: 0.0365 Epoch 13/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0247 - val_loss: 0.0358 Epoch 14/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0239 - val_loss: 0.0350 Epoch 15/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0233 - val_loss: 0.0349 Epoch 16/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0227 - val_loss: 0.0342 Epoch 17/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0221 - val_loss: 0.0340 Epoch 18/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0217 - val_loss: 0.0338 Epoch 19/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0212 - val_loss: 0.0335 Epoch 20/20 5/5 [==============================] - 0s 15ms/step - loss: 0.0209 - val_loss: 0.0334
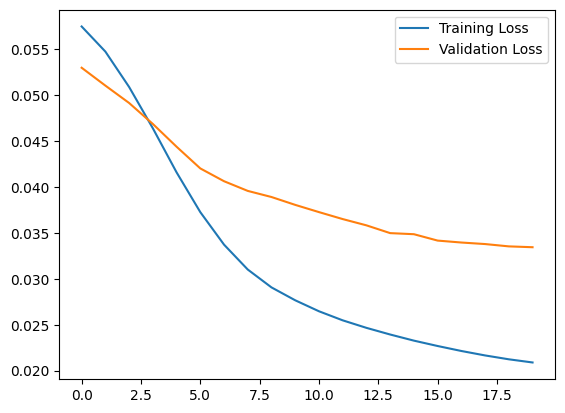
plt.plot(history.history["loss"], label="Training Loss")
plt.plot(history.history["val_loss"], label="Validation Loss")
plt.legend()
<matplotlib.legend.Legend at 0x7ff82e9b9760>
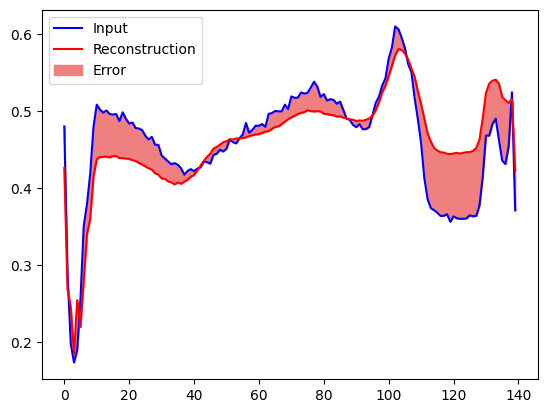
如果重构误差比正常训练样本大一个标准差,您可以快速地将心电图归类为异常。首先,我们绘制训练集中的一个正常心电图,随后绘制自编码器对其进行编码和解码后的重构以及重构误差。
encoded_data = autoencoder.encoder(normal_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(normal_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], normal_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
创建一个类似的绘图,这次是一个异常的测试样本。
encoded_data = autoencoder.encoder(anomalous_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(anomalous_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], anomalous_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
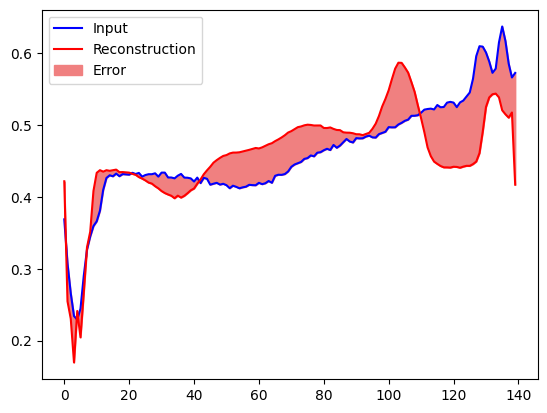
检测异常
通过计算重构损失是否大于固定阈值来检测异常。在本教程中,您将计算训练集中正常样本的平均误差,如果重构误差比训练集大一个标准差,则将未来的样本分类为异常。
根据训练集中的正常心电图绘制重构误差:
reconstructions = autoencoder.predict(normal_train_data)
train_loss = tf.keras.losses.mae(reconstructions, normal_train_data)
plt.hist(train_loss[None,:], bins=50)
plt.xlabel("Train loss")
plt.ylabel("No of examples")
plt.show()
74/74 [==============================] - 0s 1ms/step
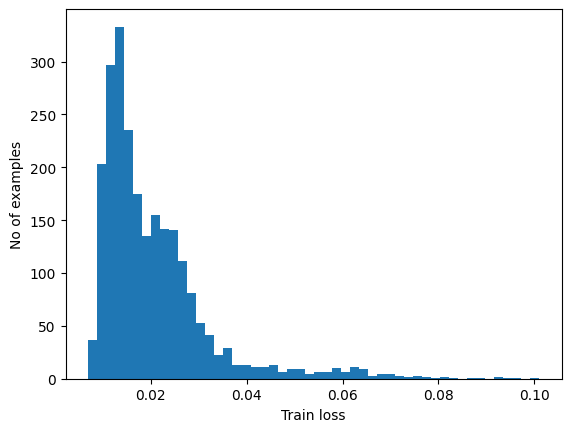
选择一个比平均值高一个标准差的阈值。
threshold = np.mean(train_loss) + np.std(train_loss)
print("Threshold: ", threshold)
Threshold: 0.032788377
注:还有其他可用来选择阈值的策略,高于该阈值时,应将测试样本分类为异常,正确的方式将取决于您的数据集。您可以通过本教程末尾的链接了解更多信息。
如果检查测试集中异常样本的重构误差,您会注意到大多数异常样本的重构误差都比阈值大。通过更改阈值,您可以调整分类器的精确率和召回率。
reconstructions = autoencoder.predict(anomalous_test_data)
test_loss = tf.keras.losses.mae(reconstructions, anomalous_test_data)
plt.hist(test_loss[None, :], bins=50)
plt.xlabel("Test loss")
plt.ylabel("No of examples")
plt.show()
14/14 [==============================] - 0s 1ms/step
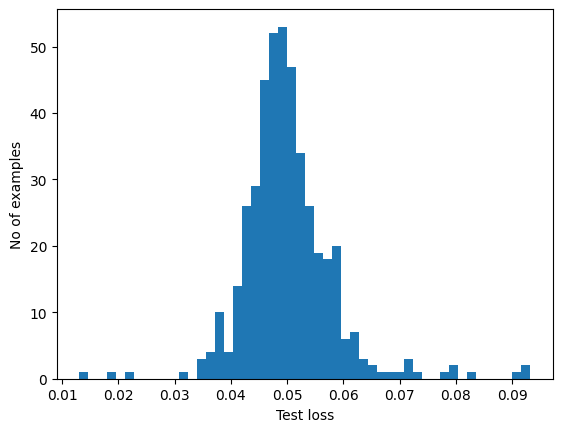
如果重构误差大于阈值,则将心电图分类为异常。
def predict(model, data, threshold):
reconstructions = model(data)
loss = tf.keras.losses.mae(reconstructions, data)
return tf.math.less(loss, threshold)
def print_stats(predictions, labels):
print("Accuracy = {}".format(accuracy_score(labels, predictions)))
print("Precision = {}".format(precision_score(labels, predictions)))
print("Recall = {}".format(recall_score(labels, predictions)))
preds = predict(autoencoder, test_data, threshold)
print_stats(preds, test_labels)
Accuracy = 0.943 Precision = 0.9921722113502935 Recall = 0.9053571428571429
后续步骤
要详细了解如何使用自编码器检测异常,请查看 Victor Dibia 使用 TensorFlow.js 构建的出色交互式示例。对于真实用例,您可以了解 Airbus 如何使用 TensorFlow 检测 ISS 遥测数据中的异常。要详细了解基础知识,请考虑阅读 François Chollet 撰写的这篇博文。有关更多详细信息,请查看 Ian Goodfellow、Yoshua Bengio 和 Aaron Courville 撰写的《深度学习》一书的第 14 章。
