Bayes modeli seçimi
 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
ithalat
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
Görev: birden çok değişiklik noktasıyla değişiklik noktası algılama
Bir değişiklik noktası algılama görevi düşünün: olaylar, veri üreten bir sistem veya işlemin (gözlemlenmeyen) durumundaki ani değişimler tarafından yönlendirilen, zaman içinde değişen bir hızda gerçekleşir.
Örneğin, aşağıdaki gibi bir dizi sayım gözlemleyebiliriz:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
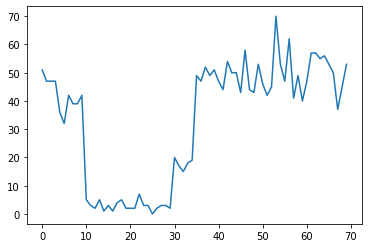
Bunlar, bir veri merkezindeki hata sayısını, bir web sayfasını ziyaret edenlerin sayısını, bir ağ bağlantısındaki paketlerin sayısını vb. temsil edebilir.
Sadece verilere bakarak kaç farklı sistem rejiminin olduğu tamamen açık değildir. Üç geçiş noktasının her birinin nerede meydana geldiğini söyleyebilir misiniz?
Bilinen eyalet sayısı
İlk olarak, gözlemlenmeyen durumların sayısının önceden bilindiği (belki de gerçekçi olmayan) durumu ele alacağız. Burada, dört gizli durum olduğunu bildiğimizi varsayarız.
Bir anahtarlama (homojen olmayan) Poisson sürecine bu sorunu modeli: zaman içinde her bir noktada meydana gelen olayların sayısı Poisson dağıtılmış ve etkinlik oranı gözlemlenmeyen sistem durumu ile tayin edilir, \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
Latent durumları ayrık: \(z_t \in \{1, 2, 3, 4\}\), bu \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) her durum için bir Poisson oranı ihtiva eden basit bir vektördür. Zamanla devletler evrimini modellemek için, basit bir geçiş modeli tanımlarsınız \(p(z_t | z_{t-1})\): en her adımda bazı olasılık ile önceki duruma kalmak diyelim \(p\)ve olasılık ile \(1-p\) bir biz geçiş rastgele rastgele farklı durum. Başlangıç durumu da rastgele rastgele seçilir, bu nedenle:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
Bu varsayımlar bir karşılık gizli Markov modeli Poisson emisyonlu. Biz kullanarak TFV onları kodlamak tfd.HiddenMarkovModel . İlk olarak, başlangıç durumundan önce geçiş matrisini ve üniformayı tanımlarız:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
Sonra, bir inşa tfd.HiddenMarkovModel her sistem durumuyla ilişkili oranlarını temsil etmek eğitilebilir bir değişkeni kullanarak, dağıtım. Pozitif değerli olduklarından emin olmak için oranları log-uzayda parametreleştiriyoruz.
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
Son olarak, oranları önce zayıf bilgilendirici lognormal de dahil olmak üzere, modelin toplam günlük yoğunluğu tanımlar ve hesaplamak için bir en iyi duruma çalıştırmak Maksimum a posteriori gözlenen sayım verileri (MAP) uyum.
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
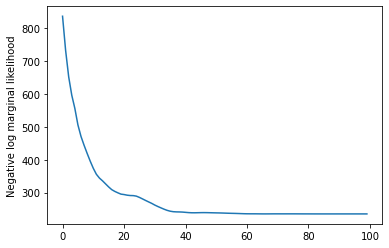
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
İşe yaradı! Bu modeldeki gizli durumların yalnızca permütasyona kadar tanımlanabilir olduğuna dikkat edin, bu nedenle kurtardığımız oranlar farklı bir sıradadır ve biraz gürültü vardır, ancak genellikle oldukça iyi eşleşirler.
Devlet yörüngesini kurtarmak
Şimdi modeli uygun ettik ki biz modeli sistemi, her timestep andaki inandığı hangi devlet yeniden isteyebilirsiniz.
Bu arka çıkarım iştir: Gözlenen sayımları verilen \(x_{1:T}\) ve model parametrelerinin (fiyatlar) \(\lambda\), biz arka dağıtımda aşağıdaki ayrık gizli değişkenlerin sırasını anlaması istediğiniz \(p(z_{1:T} | x_{1:T}, \lambda)\). Gizli bir Markov modelinde, standart mesaj iletme algoritmalarını kullanarak bu dağılımın marjinallerini ve diğer özelliklerini verimli bir şekilde hesaplayabiliriz. Özellikle, posterior_marginals yöntem etkili bir şekilde (kullanarak hesaplamak ileri-geri bir algoritma marjinal olasılık dağılımı) \(p(Z_t = z_t | x_{1:T})\) ayrık gizli durumu üzerinde \(Z_t\) her timestep de \(t\).
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
Sonsal olasılıkları çizerek, modelin verilere ilişkin "açıklamasını" elde ederiz: her bir durum zamanın hangi noktalarında etkindir?
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
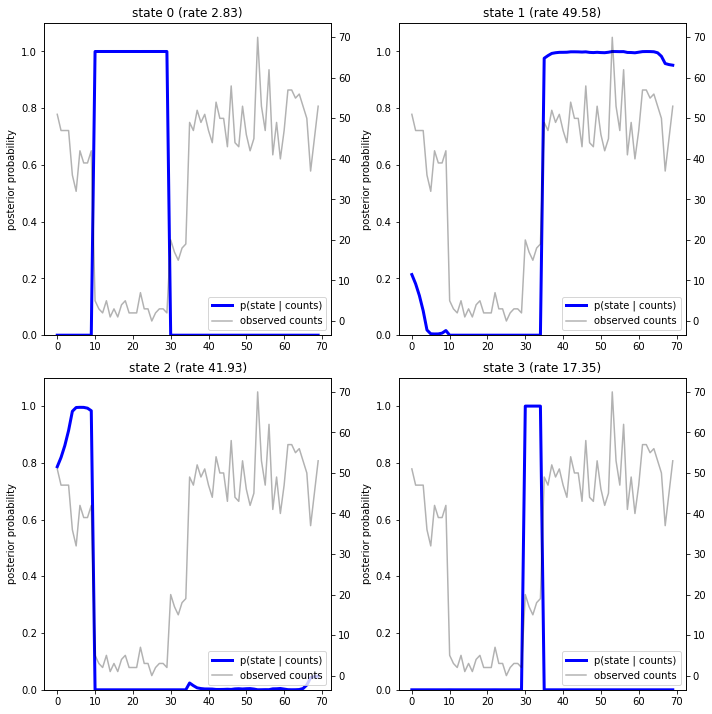
Bu (basit) durumda, modelin genellikle oldukça emin olduğunu görüyoruz: çoğu zaman adımında, esas olarak tüm olasılık kütlesini dört durumdan tek birine atar. Neyse ki, açıklamalar makul görünüyor!
Ayrıca, tek bir açıklama içine olasılıksal posterior yoğuşmalı, her timestep en büyük olasılıkla gizli devlet ile ilişkili oranı açısından bu posterior görselleştirmek:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
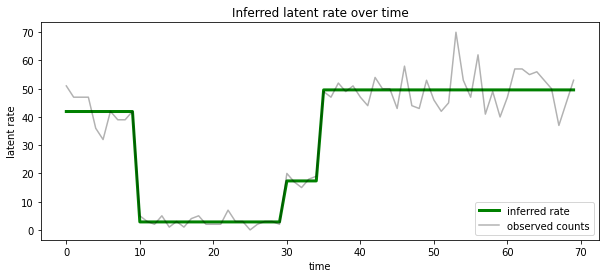
Bilinmeyen sayıda eyalet
Gerçek problemlerde, modellediğimiz sistemdeki 'gerçek' durum sayısını bilemeyebiliriz. Bu her zaman bir endişe kaynağı olmayabilir: Bilinmeyen durumların kimliklerini özellikle umursamıyorsanız, modelin ihtiyaç duyacağını bildiğinizden daha fazla durum içeren bir model çalıştırabilir ve bir sürü kopya (gibi bir şey) öğrenebilirsiniz. gerçek durumların kopyaları. Ancak, 'gerçek' gizli durum sayısını çıkarmayı umursadığınızı varsayalım.
Biz bir vaka olarak bu görüntüleyebilirsiniz Bayes modeli seçimi : Biz aday bir dizi model, gizli durumlarının farklı bir sayı ile her var ve büyük olasılıkla gözlenen veriler üretilmiştir için birini seçmek istiyorum. Bunu yapmak için, biz de modellere kendileri üzerindeki bir önceki ekleyebilir (her modelin altında verilerin marjinal ihtimalini hesaplamak, ama bu analizde gerekli olmayacak; Bayes Occam'ın jilet kodlamak a yeterli olarak çıkıyor daha basit modelleri tercih edin).
Ne yazık ki, ikisi üzerinde bütünleştirir ayrık devletler gerçek marjinal olabilirlik, \(z_{1:T}\) ve (vektörü) oranı parametreleri \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) bu model için uysal değildir. Kolaylık sağlamak için, bir sözde "kullanarak yaklaşır edeceğiz ampirik Bayes " veya tahmin "II maksimum olabilirlik yazın": yerine tamamen (bilinmeyen) oranı parametrelerini entegre \(\lambda\) her sistem durumuyla ilişkili, biz optimize ederiz değerlerinin üzerinde:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
Bu yaklaşım fazla gelebilir, yani gerçek marjinal olasılığın yapacağından daha karmaşık modelleri tercih edecektir. Bir bağlanmış düşük Varyasyon optimize veya Monte Carlo tahmin gibi kullanan, örneğin, daha sadık yaklaşımları, düşünebiliriz tavlanmış önem örnekleme ; bunlar (ne yazık ki) bu defterin kapsamı dışındadır. (Bayes modeli seçimi ve yaklaşımlar, mükemmel bölüm 7 hakkında daha fazlası için Makine Öğrenmesi: Bir Olasılık Perspektif iyi referanstır.)
Prensip olarak, biz sadece farklı değerlerle birçok kez yukarıda optimizasyonu çalıştırarak bu model karşılaştırma yapabileceği num_states , ama bu çok iş olacaktır. Burada TFP en kullanılarak paralel çoklu modellerini dikkate almak nasıl göstereceğiz batch_shape vektörleştirme için mekanizma.
Geçiş matrisi ve ilk durumu önceki: yerine tek bir model açıklaması yapı yerine, artık geçiş matrisler ve önceki logits, her aday modeli üstü için bir toplu oluşturmak gerekir max_num_states . Kolay gruplama için tüm hesaplamaların aynı 'şekle' sahip olduğundan emin olmamız gerekecek: bu, sığdıracağımız en büyük modelin boyutlarına karşılık gelmelidir. Daha küçük modelleri ele almak için, açıklamalarını durum uzayının en üst boyutlarına 'gömebiliriz', kalan boyutları etkin bir şekilde hiç kullanılmayan kukla durumlar olarak ele alabiliriz.
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
Şimdi yukarıdakine benzer şekilde ilerliyoruz. Bu sefer fazladan bir toplu boyut kullanacağız trainable_rates ayrı ayrı dikkate alınan her model için fiyat uygun.
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
Toplam log probunu hesaplarken, her bir model bileşeni tarafından fiilen kullanılan oranların sadece önceliklerini toplamaya özen gösteriyoruz:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
Şimdi aynı anda tüm aday modellerini uydurma, biz inşa ettik toplu hedefi optimize:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
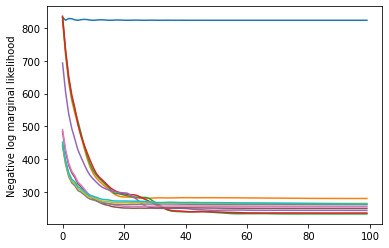
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
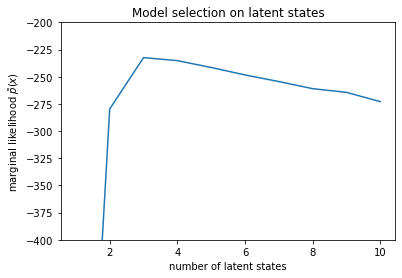
Olasılıkları incelediğimizde, (yaklaşık) marjinal olasılığın üç durumlu bir modeli tercih etme eğiliminde olduğunu görüyoruz. Bu oldukça makul görünüyor -- 'doğru' modelin dört durumu vardı, ancak sadece verilere bakarak üç durumlu bir açıklamayı dışlamak zor.
Ayrıca her aday model için uygun oranları da çıkarabiliriz:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
Ve her modelin veriler için sağladığı açıklamaları çizin:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
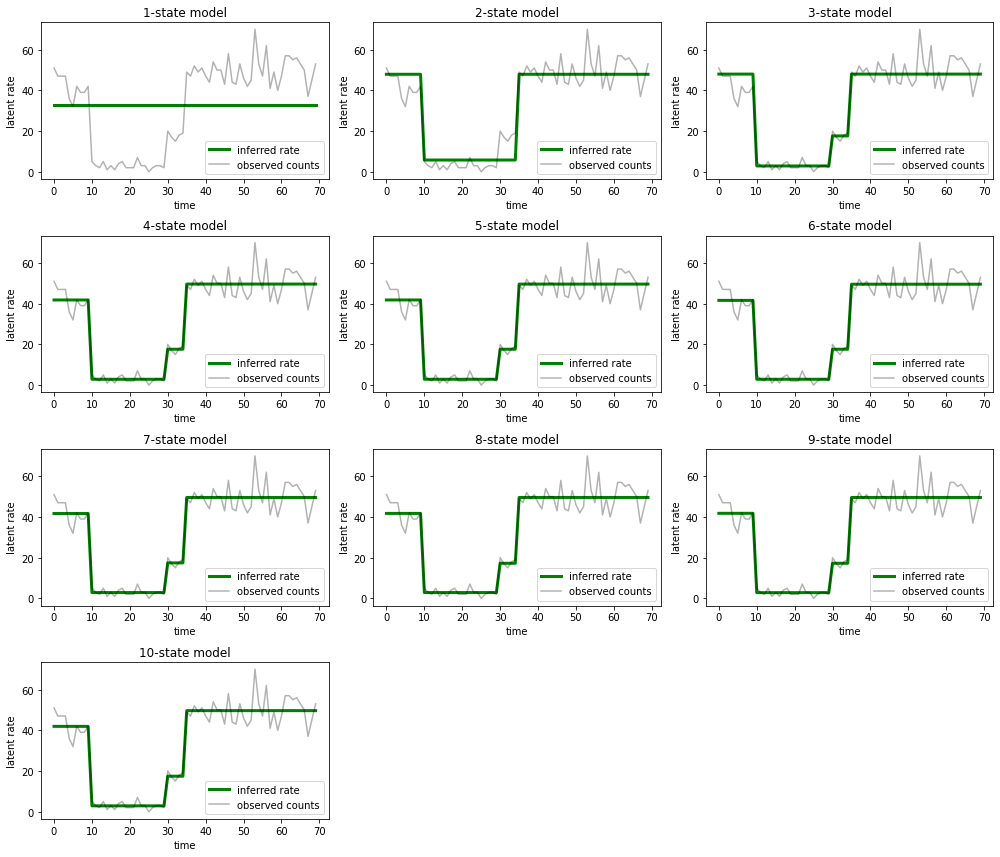
Bir, iki ve (daha kurnazca) üç durumlu modellerin nasıl yetersiz açıklamalar sağladığını görmek kolaydır. İlginç bir şekilde, dört durumun üzerindeki tüm modeller temelde aynı açıklamayı sağlar! Bunun nedeni, 'verilerimizin' nispeten temiz olması ve alternatif açıklamalar için çok az yer bırakması olabilir; daha karmaşık gerçek dünya verilerinde, daha yüksek kapasiteli modellerin verilere aşamalı olarak daha iyi uyum sağlamasını beklerdik, gelişmiş uyumun model karmaşıklığından daha ağır bastığı bazı ödünleşme noktaları ile.
Uzantılar
Bu defterdeki modeller birçok yönden basit bir şekilde genişletilebilir. Örneğin:
- gizli durumların farklı olasılıklara sahip olmasına izin vermek (bazı durumlar nadir veya yaygın olabilir)
- gizli durumlar arasında tek biçimli olmayan geçişlere izin verilmesi (örneğin, bir makine çökmesinin genellikle bir sistem yeniden başlatılmasının ardından geldiğini öğrenmek, genellikle bir iyi performans periyodu vb.)
- Diğer emisyon modelleri, mesela
NegativeBinomialgibi sayım verileri veya sürekli dağılımlar içinde dağılımlar değişen modelNormalgerçek değerli veriler için.
